Стандартные криптографические алгоритмы цифровой подписи

В настоящее время очень развиты всевозможные коммуникационные сети. В связи с этим выросли объёмы передаваемых данные через незащищённые сети, устройства и т.д. Одним из способов обеспечения подлинности передаваемых данных, наряду с шифрованием и хешированием, является электронная цифровая подпись.

Цифровая подпись по сути является аналогом подписи от руки, т.е. позволяет однозначно идентифицировать отправителя сообщения. Использование электронной подписи позволяет осуществить контроль целостности передаваемого документа, защиту от изменений (подделки)

документа, невозможность отказа от авторства и доказательное подтверждение авторства документа

Существует несколько схем построения цифровой подписи:

• 1.    На основе алгоритмов симметричного шифрования. Данная схема предусматривает наличие в системе третьего лица — арбитра, пользующегося доверием обеих сторон. Авторизацией документа является сам факт зашифрования его секретным ключом и передача его арбитру.

• 2.    На основе алгоритмов асимметричного шифрования. На данный момент такие схемы ЭП наиболее распространены и находят широкое применение.

Поскольку подписываемые документы — переменного (и как правило достаточно большого) объёма, в схемах ЭП зачастую подпись ставится не на сам документ, а на его хеш. Для вычисления хэша используются криптографические хеш-функции, что гарантирует выявление изменений документа при проверке подписи. Хеш-функции не являются частью алгоритма ЭП, поэтому в схеме может быть использована любая надёжная хеш-функция.

Стандарты, рассматриваемые в рамках данного курсового проекта, реализуют ассиметричные алгоритмы создания цифровой подписи. В отличие от асимметричных алгоритмов шифрования, в которых шифрование производится с помощью открытого ключа, а расшифровка — с помощью закрытого, в схемах цифровой подписи подписание производится с применением закрытого ключа, а проверка подписи — с применением открытого.

Общепризнанная схема цифровой подписи охватывает три процесса:

• 1.    Генерация ключевой пары. При помощи алгоритма генерации ключа равновероятным образом из набора возможных закрытых ключей выбирается закрытый ключ, вычисляется соответствующий ему открытый ключ.

• 2.    Формирование подписи. Для заданного электронного документа с помощью закрытого ключа вычисляется подпись.

• 3.    Проверка (верификация) подписи. Для данных документа и подписи с помощью открытого ключа определяется действительность подписи.

Рассмотрим каждый алгоритм поподробнее

RSA

RSA (аббревиатура от фамилий Rivest, Shamir и Adleman) — криптографический алгоритм с открытым ключом, основывающийся на вычислительной сложности задачи факторизации больших целых чисел.

Т.к. является ассиметричным алгоритмом, он основывается на генерации открытого и закрытого ключей, которые непосредственно участвуют в шифровании данных.

В основу криптографической системы с открытым ключом RSA положена сложность задачи факторизации произведения двух больших простых чисел. Для шифрования используется операция возведения в степень по модулю большого числа. Для дешифрования за разумное время (обратной операции) необходимо уметь вычислять функцию Эйлера от данного большого числа, для чего необходимо знать разложения числа на простые множители.

В криптографической системе с открытым ключом каждый участник располагает как открытым ключом (англ. public key), так и закрытым ключом (англ. private key). В криптографической системе RSA каждый ключ состоит из пары целых чисел. Каждый участник создаёт свой открытый и закрытый ключ самостоятельно. Закрытый ключ каждый из них держит в секрете, а открытые ключи можно сообщать кому угодно или даже публиковать их. Открытый и закрытый ключи каждого участника обмена сообщениями в криптосистеме RSA образуют «согласованную пару» в том смысле, что они являются взаимно обратными, то есть:

V допустимых пар открытого и закрытого ключей (р, s')

• 3    соответствующие функции шифрования Е_р(х) и расшифрования D_s(x) такие, что

• V сообщений т ЕМ, где М — множество допустимых сообщений, т = Ds (Ер(т)) = EP(Ds(m))

Алгоритм создания открытого и секретного ключей

RSA-ключи генерируются следующим образом:

• 1.    Выбираются два различных случайных простых числа p и q заданного размера (например, 1024 бита каждое).

• 2.   Вычисляется их произведение п = р • q, которое называется

• 3.   Вычисляется значение функции Эйлера от числа п: р(п) =

• 4.    Выбирается целое число е (1 < е < р(п)), взаимно простое со значением функции р(п), Обычно в качестве е берут простые числа, содержащие небольшое количество единичных бит в двоичной записи, например, простые числа Ферма 17, 257 или 65537.

модулем.

⁽р - V⁽q - 1)

• a.    Число e называется открытой экспонентой (англ. public exponent)

• b.    Время, необходимое для шифрования с использованием быстрого возведения в степень, пропорционально числу единичных бит в e.

• c.    Слишком малые значения e, например 3, потенциально могут ослабить безопасность схемы RSA.

• 5.    Вычисляется число d, мультипликативно обратное к числу е по модулю р(п),то есть число, удовлетворяющее условию:

d • e = 1 mod p(n)

• a.    Число d называется секретной экспонентой. Обычно, оно вычисляется при помощи расширенного алгоритма Евклида.

• 6.    Пара {e, n} публикуется в качестве открытого ключа RSA (англ. RSA public key).

• 7.    Пара {d, n} играет роль закрытого ключа RSA (англ. RSA private key) и держится в секрете.

После получения пары ключей, можно переходить непосредственно к созданию цифровой подписи

Алгоритм создания подписи

• 1.    Взять открытый текст m - для него будет создаваться цифровая подпись

• 2.    Создать цифровую подпись с помощью своего секретного ключа {d,s} по формуле: s = S_A(m) = m^d mod n

• 3.    Отправить получателю сообщения пару {m,s} состоящую из сообщения и подписи

Алгоритм проверки подлинности подписи

• 1.   Принять пару {m,s}

• 2.    Получить открытый ключ {e,n} отправителя сообщения

• 3.   Вычислить прообраз сообщения из подписи

• 4.    Проверить подлинность подписи и неизменность сообщения сравнив m и m’

m ' = P_A(s) = s^e mod n

ECDSA

ECDSA (Elliptic Curve Digital Signature Algorithm) — алгоритм с открытым ключом для создания цифровой подписи, относится к эллиптической криптографии.

Эллиптическая криптография — раздел криптографии, который изучает асимметричные криптосистемы, основанные на эллиптических кривых над конечными полями. Основное преимущество эллиптической криптографии заключается в том, что на сегодняшний день неизвестно существование субэкспоненциальных алгоритмов решения задачи дискретного логарифмирования.

Асимметричная криптография основана на сложности решения некоторых математических задач. Ранние криптосистемы с открытым ключом, такие как алгоритм RSA, безопасны благодаря тому, что сложно разложить составное число на простые множители. При использовании алгоритмов на эллиптических кривых полагается, что не существует субэкспоненциальных алгоритмов для решения задачи дискретного логарифмирования в группах их точек. При этом порядок группы точек эллиптической кривой определяет сложность задачи. Считается, что для достижения такого же уровня безопасности как и в RSA требуются группы меньших порядков, что уменьшает затраты на хранение и передачу информации.

Эллиптические кривые над конечными полями

Эллиптической кривой называется множетсво точек (х, у) удовлетворяющих условию :

у2 + а1ху + а3у = х3 + а2х2 + а4х + а6

Это уравнение может рассматриваться над произвольными полями и, в частности, над конечными полями, представляющими для криптографии особый интерес.

В криптографии эллиптические кривые рассматриваются над двумя типами конечных полей: простыми полями нечётной характеристики (Z_p, где р > 3 — простое число) и полями характеристики 2 (GF(2^m)).

Над полем Z_p характеристики р > 3 уравнение эллиптической кривой E можно привести к виду:

Е: у² = х³ + Ах + В ( mod р )

гдеА,В Е Z p — константы, удовлетворяющие условию 4А³ + 27В² ^ 0 (mod р)

Группой точек эллиптической кривой Е над полем Z p называется множество пар (х, у) лежащих на Е, объединённое с нулевым элементом О:

E(Zp') = О U {(х,у) Е Z_p х Z_p\у² = х³ + Ах + В (mod р)}

Точка эллиптической кривой обозначается Q(x, y) или просто Q. Две точки эллиптической кривой равны, если равны их соответствующие х и у координаты.

На множестве всех точек эллиптической кривой Е операцию сложения обозначают знаком «+». Для двух произвольных точек Q1(x1 ,y1 ) и Q2( x2,y2 ) эллиптической кривой E рассмотривают несколько случаев.

Для точек Q1 и Q2, координаты которых удовлетворяют условию х1 Ф х2, их суммой называется точка Q3(x3 , y3), координаты которой определяются сравнениями

( х₃ = Л² — х 1 — х₂ (mod р)

{у 3 =Л⁽х₁ — х 3 ⁾—у₁ (mod р)

где Л = ^{У 2 У1} (mod р)

Х 2 -Х 1

Если выполнены равенства х 1 = х₂ и у 1 = у₂ Ф 0 , то координаты точки

Q3 определяются следующим образом:

( х₃ = Л² — 2х 1 (mod р)

I у 3 = Л⁽х 1 — х 3^ — у 1 (mod р)

где Л =

3х 2 +а

2У 1

(mod р)

Если выполнены условия Х 1 = х₂ и у 1 =

—у₂ (mod р) , то сумма точек

Q1 и Q2 называется нулевой точкой О без определения ее х – и у – координат.

В этом случае точка Q2 называется отрицанием точки Q1. Для нулевой точки О выполнены равенства

q+O=O+Q=Q

где Q – произвольная точка на эллиптической кривой E.

Генерирование ключей

Для подписывания сообщений необходима пара ключей — открытый и закрытый. При этом закрытый ключ должен быть известен только тому, кто подписывает сообщения, а открытый — любому желающему проверить подлинность сообщения. Также общедоступными являются параметры самого алгоритма.

Параметры алгоритма

• 1.    Выбор хэш-функции H(x). Для использования алгоритма необходимо, чтобы подписываемое сообщение являлось числом. Хеш-функция должна преобразовать любое сообщение в последовательность битов, которые можно потом преобразовать в число.

• 2.    Выбор большого простого числа q — порядок одной из циклических подгрупп группы точек эллиптической кривой.

• 3.    Простым числом p обозначается характеристика поля координат F_p .

Замечание: Если размерность этого числа в битах меньше размерности в битах значений хэш-функции H(x) то используются только левые биты значения хэш-функции .

Для простоты будем рассматривать эллиптические кривые над полем F p , где F_p — конечное простое поле. Причем, если необходимо, конструкцию можно легко адаптировать для эллиптических кривых над другим полем.

Пусть E — эллиптическая кривая, определенная над F p , и P — точка простого порядка q кривой E( F p ). Кривая E и точка P являются системными параметрами. Число p — простое. Каждый пользователь конструирует свой ключ посредством следующих действий:

• 1.    Выбирает случайное или псевдослучайное целое число x из интервала [1,q-1].

• 2.    Вычисляет произведение (кратное) Q = x·P.

Открытым ключом пользователя является точка Q, а закрытым — x.

Вычисление цифровой подписи

Для того, чтобы подписать какое-либо сообщение, для которого подсчитано значение h хэш-функции H, пользователь A должен сделать следующее:

• 1.    Выбрать случайное целое число к Е [1,q — 1].

• 2.    Вычислить к • Р = (х₁,у₁) и положить r= x 1 mod q, где r получается из целого числа х 1 между 0 и (p - 1) приведением по модулю q. Если r = 0, то вернуться на шаг 1

• 3.    Вычислить к^-1 (mod q) и положить s= k^-1(h + x^r) mod q, где h — значение хеш-функции подписываемого сообщения. В случае s = 0 необходимо вернуться к шагу 1.

Подписью для сообщения является пара целых чисел (r, s)

Проверка цифровой подписи

Для того, чтобы проверить подпись пользователя (r, s) на отправленное сообщение, получатель должен сделать следующее:

• 1.   Получить подтвержденную  копию открытого  ключа  Q

• 2.   Проверить, что числа r и s являются целыми числами из

• 3.   Вычислить u 1 = s^h mod q и u₂ = s^-1r mod q;

• 4.    Вычислить u 1 • Р + u₂ • Q = (x₀, у₀, и относительнох₀, как целого

• 5.    Принять подпись, если и только если v = r.

пользователя А;

интервала [1, q — 1], и вычислить значение хеш-функции h от сообщения;

числа между 0 и (р — 1), положить v = х₀ mod q

Для подтверждения публичного ключа Q нужно проделать следующее (O здесь обозначает бесконечно удалённую точку):

• 1.   Проверить, что Q не равно O и координаты верны;

• 2.   Проверить, что Q лежит на кривой;

• 3.    Проверить, что qQ = O;

СТБ 34.101.45, ДСТУ 4145-2002, ГОСТ Р34.10-2012

Данные три стандарта не зря объединены под одной главой. Стандарт ГОСТ P34.10-2012, является практически полной копией стандарта ECDSA принятого в стандартах ANSI и ISO. ГОСТ основан на эллиптических кривых. Стойкость алгоритмов основывается на сложности вычисления дискретного логарифма в группе точек эллиптической кривой, а также на стойкости хэш-функции. Для ГОСТ Р 34.10-2012 используется хэш-функция по ГОСТ Р 34.11-2012. Одно отличие от стандарта ECSDA заключается в том, что значение хэш-функции берется по модулю q, т.е. байты не сдвигают вправо в случае если количество бит хэша больше, а преобразуют число сразу. В остальном генерация ключей, вычисление подписи, проверка идентичны.

Белорусский СТБ и украинский ДСТУ аналогично являются копиями стандарта ГОСТ

Реализация алгоритмов

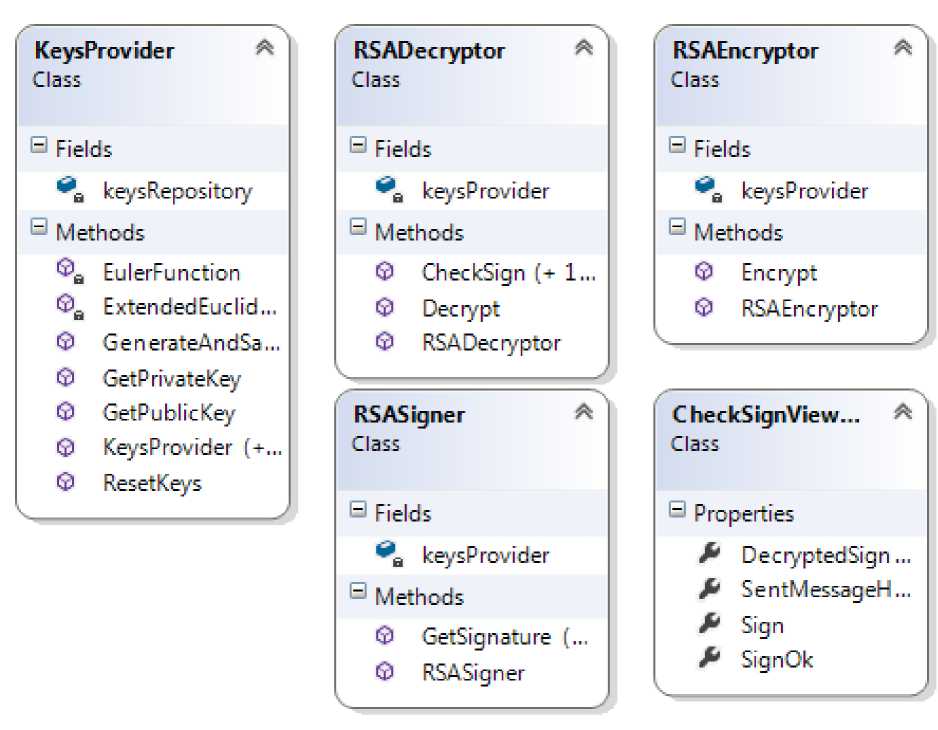
Диаграмма классов

Л Sign Ok curveProvider

S private curveProvider

ExtendedEuclid...

curveProvider keysProvider

ExtendedEuclid...

Классы для алгоритма RSA

®

s publicKey x Private

CheckSign

ECDSAVerifier

“ public

О c и public

A MessageHash

GenerateAndSa...

GetPrivateKey GetPublicKey KeysProvider

• 1.    KeysProvider – генерирует и хранит в себе открытый и закрытый ключи, в случае необходимости их можно сбросить и автоматически создадутся новые

• 2.    RSASigner – класс который подписывает подающуюся на вход строку, на выходе – цифровая подпись

• 3.    RSADecryptor – класс для проверки цифровой подписи, на вход подпись, сообщение и открытый ключ, на выходе класс CheckSignViewModel, который хранит статус проверки

• 4.    RSAEncryptor – класс для шифрования информации по алгоритму RSA

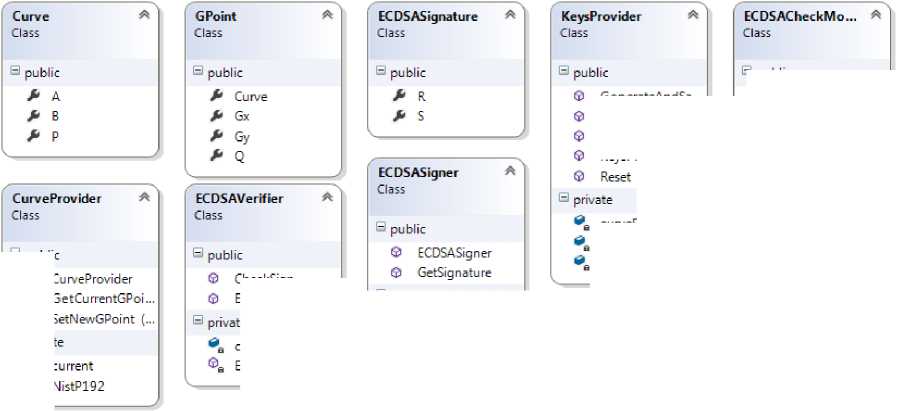
Классы для алгоритма ECDSA

• 1.    Curve – класс для представления эллиптической кривой, содержит основные достаточные параметры для ее определения

• 2.    GPoint – класс для представления точки на кривой, основной нужный нам параметр – Q – порядок точки на кривой

• 3.    ECDSASignature – класс для представления цифровой подписи

• 4.    KeysProvider – генерирует и хранит в себе открытый и закрытый ключи, в случае необходимости их можно сбросить и автоматически создадутся новые

• 5.    CurveProvider – класс, хранит в себе текущую эллиптическую кривую, кривые выбираются из списка рекомендованных Национальным Институтом Стандартов и Технологий (США)

• 6.    ECDSACheckModel – класс который хранит в себе статус проверки присланной цифровой подписи, так же ключи и хэш сообщения

• 7.    ECDSASigner – класс который подписывает подписью подаваемую на вход строку

• 8.    ECDSAVerifier – класс который проверяет цифровую подпись. На вход подпись, сообщение и открытый ключ отправителя.

Пример реализации public class KeysProvider

{ private ECDSAPublicKey publicKey;

private BigInteger xPrivate;

private CurveProvider curveProvider;

public KeysProvider(CurveProvider curveProvider)

{ this.curveProvider = curveProvider;

GenerateAndSaveKeys();

} public void GenerateAndSaveKeys()

{ var q = curveProvider.GetCurrentGPoint.Q;

var xBytes = new byte[q.ToByteArray().Length];

rand.GetNonZeroBytes(xBytes);

var x = BigInteger.Remainder(new BigInteger(xBytes), q - 2) + 1;

if (x.Sign == -1) x *= -1;

var Q = new ECDSAPublicKey

{

};

this.publicKey = Q;

this.xPrivate = x;

} public ECDSAPublicKey GetPublicKey() { return publicKey;

} public BigInteger GetPrivateKey()

{ return xPrivate;

} public void Reset()

{

GenerateAndSaveKeys();

}

}

Метод класса ECDSASigner для получения подписи public ECDSASignature GetSignature(string message)

{ var q = curveProvider.GetCurrentGPoint.Q;

var                          hash                          = shaService.ComputeHash(Encoding.Unicode.GetBytes(message));

var hashNumber = new BigInteger(hash);

var                z                =                new

while (true)

{ var kBytes = new byte[q.ToByteArray().Length];

rand.GetNonZeroBytes(kBytes);

var k = BigInteger.Remainder(new BigInteger(kBytes), q - 2) + 1;

if (k.Sign == -1) k *= -1;

var Q = new ECDSAPublicKey {

};

var r = BigInteger.Remainder(Q.X, q);

if (r == 0)

{ continue;

} var s = (ExtendedEuclidFindInverseModularNumber(k%q, q) *

BigInteger.Remainder((z + r*keysProvider.GetPrivateKey()), q)) % q;

return new ECDSASignature {R = r, S = s};

}

Метод класса EСDSAVerifier для проверки цифровой подписи public ECDSACheckModel CheckSign(string message, ECDSASignature signature, ECDSAPublicKey qPublicKey)

{ var q = curveProvider.GetCurrentGPoint.Q;

var                          hash                          = shaService.ComputeHash(Encoding.Unicode.GetBytes(message));

var hashNumber = new BigInteger(hash);

var                z                =                new

if (signature.R < 1 || signature.R > curveProvider.GetCurrentGPoint.Q

- 1)

{ return new ECDSACheckModel

{

MessageHash = hashNumber,

Sign = signature,

SignOk = false

};

} if (signature.S < 1 || signature.S > curveProvider.GetCurrentGPoint.Q - 1)

{ return new ECDSACheckModel

{

MessageHash = hashNumber,

Sign = signature,

SignOk = false };

} var w = ExtendedEuclidFindInverseModularNumber(signature.S%q, q);

var u1 = (z*w)%q;

var u2 = (signature.R*w)%q;

var curvePoint = new ECDSAPublicKey {

return new ECDSACheckModel

{

MessageHash = hashNumber, Sign = signature,

SignOk = signature.R == curvePoint.X%q

};

}

Заключение

Было рассмотрено 5 стандартов цифровой подписи основанных на асимметрических алгоритмах с использованием и без эллиптических кривых. 2 алгоритма – RSA и ECDSA – были реализованы програмно, опробованы и протестированы. В ходе тестирования выяснилось, что алгоритм RSA и ECDSA достигают одинакового криптостойкости при абсолютно разных затратах памяти и времени. Так RSA нужно примерно в 4 раза больше памяти для ключей и куда больше времени для их генерации и процесса создания подписи. Ускорить работу алгоритма можно за счет использования параллельных вычислений на многоядерных машинах, однако неоспоримым остается факт, что криптосистемы основанные на эллиптических прямых имеют гораздо больше преимуществ и за ними будущее (и уже настоящее) криптографии