Стандартные теплоемкости и энтропии карбидов хрома переменного состава

Теплоемкость и энтропия веществ и их изменение в тепловых процессах являются важнейшими термическими характеристиками. Зависимости энтальпии и энергии Гиббса от температуры определяются температурными зависимостями теплоемкости и энтропии.

Несостоятельность прямой аддитивности или их инкрементов при расчете теплоемкости или энтропии сложных веществ количественно показана в [1,2].

Для бинарных систем АВ_Х, в которых компонент В при стандартных условиях является газом, разработаны корректные модели расчета С° и S⁰ в зависимости от состава [1,3-5].

Несомненный интерес и актуальность представляет создание моделей расчетов теплоемкости и энтропии бинарных кристаллических соединений МвуА_х (MeAz/y или МеА^, в которых А является твердым веществом при стандартных условиях (С, Si, Р, В и т.п.).

Теоретическое и практическое значение в первую очередь имеет создание такой модели для веществ, содержащих углерод, в частности, карбидов. В качестве объектов изучения взяты карбиды хрома.

Соединения СгСх имеют большое практическое значение для производства металлического хрома, в металлургии хромистых сталей и ферросплавов с хромом. В справочной литературе приводятся данные для пяти кристаллических карбидов хрома: Сг4С, Сг23С6, Сг5С2, Сг7С3 и Сг3С2. Кроме того, имеются неподтвержденные сведения о существовании Сг6С и Сг3С.

Карбиды хрома благодаря ряду ценных свойств, а именно: высокая твердость при комнатных и высоких температурах, высокое сопротивление окислению, стойкость против абразивного износа и коррозии, нашли весьма широкое применение при производстве металлокерамических сплавов и для других целей. Промышленное производство карбидов хрома (в виде порошков) осуществляется путем карбонизации смеси оксида хрома Сг2О3 с углеродом при высоких температурах в атмосфере водорода [6].

Среди разнообразных направлений использования хрома наибольший удельный вес занимает производство ферросплавов. Сортамент феррохрома очень разнообразен. Существует 17 марок феррохрома и 5 марок металлического хрома. Сплавы отличаются в основном по содержанию углерода, которое изменяется от 0,01 до 8,0 % Серия «Металлургия», выпуск 6

(масс.). Высокоуглеродистый феррохром имеет в своем составе углерод в основном виде (Cr, Fe)7C3, а рафинированный содержит углерод в виде (Сг, Ге)23Сб [7]. Изучение термодинамических условий восстановления Сг2О3 углеродом осложняется отсутствием термических характеристик для карбидов хрома произвольного состава.

ТЕПЛОЕМКОСТЬ

Математическая модель

Математическая модель расчета теплоемкости кристаллических соединений обоснована и подтверждена многочисленными справочными данными на примерах оксидов s-, р- и ^-элементов произвольного состава, а также на трехкомпонентных оксидных ферри- и хромпшинелях, ильменитах [1, 3, 8]. Эта модель успешно использована при расчетах теплоемкости кристаллических нитридов марганца произвольного состава [5].

Кислород и азот при стандартных условиях представляют собой газы и, следовательно, не могут быть кристаллообразующими. Иначе обстоит дело, когда в соединении МеА_х при стандартных условиях А находится в кристаллическом состоянии, то есть может само выступать в роли КО наряду с металлом или в противовес ему.

Основные положения математической модели для расчета теплоемкости бинарных оксидов и нитридов металлов, изложенные в [1, 3, 8] применимы и для карбидов.

• 1.    Поле диаграммы «свойство-состав» делится на области твердых растворов (ОТР), в каждой из которых выделяется центральное кристаллообразующее (КО) вещество. Как правило, в роли КО выступает устойчивое соединение с известной структурой и термическими характеристиками. В первой OTP (ОТР-1) в качестве кристаллоообра-зующего выступает сам металл.

• 2.    Аддитивностью обладают величины обратных теплоемкостей. Величина обратной теплоемкости твердого раствора имеет размерность моль-К-Дж^-1. Она складывается из обратной величины теплоемкости кристаллообразующего компонента и обратной величины суммы теплоемкостей составляющих элементов с учетом объемной структурной постоянной К, включающей линейные структурные константы компонентов к. Физический смысл этой величины - изменение температуры моля вещества при сообщении ему одного джоуля энергии. Все расчеты проводятся на 1 моль металла, то есть для соединений состава МеА_х.

Аналитическое выражение модели для любой ОТР имеет вид:

(о где х„ - координата границы рассматриваемой ОТР.

Уравнение (1) можно привести к более удобному линейному виду:

• С”¹ ^МеА_х ^ = а±Ьх.

В табл. 1 (колонка 3) приведены имеющиеся справочные данные [9-12] для карбидов, расположенных в порядке увеличения содержания углерода в расчете на 1 моль металла.

Из анализа этих данных (колонки 1 и 2) следует, что в системе Сг-С должны существовать две области твердых растворов.

ОТР-1: Сг(ОЦК-2) - Сг₄С(ГЦК-4, ОЦК-1) - Сг₂₃С₄(ГЦК-4) - Сг₅С₂(ГПУ-1);

ОТР-2: Сг5С2(ГПУ-1) - Сг7С3(ГПУ-8) -Сг3С2(ромб.-4).

Цифрами отмечены числа формульных единиц (координационные числа) структур.

В ОТР-1 объединяются карбиды с кубической структурой, в ОТР-2 - с более сложными структурами (ГПУ и ромбической). На границе областей расположен карбид Сг5С2 (ГПУ-1).

По мере увеличения содержания углерода изменяется характер атомно-молекулярного взаимодействия, что приводит к преобразованию пространственного расположения частиц, то есть к постепенному переходу от одной кристаллической формации к другой с изменением линейных структурных констант кп. Поэтому в каждой ОТР объемные структурные постоянные К„ имеют свои численные значения.

ОТР-1 (х = 0+0.4). КО - Сг

Переходу от Сг (ОЦК-2), к_Оц_К = ^/З -1 ] к Сг₅С₂ (ГПУ-1), к_ГПУ__х=^- (координационное число к_от=4) соответствует объемная структурная постоянная К_х = к_оцк' ^гпу-1 ' ^ккч ⁼ = Uy-i\ — -4 = 1,79315.

• Ур. (1) принимает вид:

1,79315(0,4-8,554 + 23,550)

C;*(CrCj= 0,04246-0,02163х.    (2)

Результаты расчетов по уравнению (2) даны в табл. 1 и на рис. 1.

ОТР-2 (х = 0,4+0,66667). КО - Сг₇С₃

В качестве кристаллообразующего выбран хорошо изученный карбид Сг7С3. переходу от

, V6

структуры Сг₇С₃(ГПУ-8) крпУ-8 ⁼--- ^к ромби-

Таблица1

Стандартная теплоемкость карбидов хрома

	Вещество	Структура	С° [9-12]	С-1	С-1 ур.(2,3)	z-<0 Ср.расч.
	1	2	3	4	5	6
1	С	ГПУ-4	8,554+0,167
2	Сг	ОЦК-2 («■Fe)	23,550+0,126	0,04246+0,00022	0,04246 (2)	23,552
3	Сг4С СгСо25	ОЦК-1 ГЦК-4	107,816+0,418 26,954+0,105	0,03710+0,00014	0,03705 (2)	107,955 26,989
4	Сг23Сб СгСо,26087	ГЦК-4	624,253+2,929 27,141+0,128	0,03684+0,00018	0,03682 (2)	624,660 27,159
5	Сг5С2 СгС0,4	ГПУ-2	147,695+1,255 29,539+0,251	0,03385+0,00028	0,03381 (2) 0,03386 (3)	147,885 29,577 147,665 29,533
6	Сг7С3 СгС0.42857	ГПУ-8	208,865+0,837 29,838+0,119	0,03351+0,00013	0,03351 (3)	208,901 29,843
7	Сг3С2 СгСо.66667	ромб.-4	98,150+0,209 32,817+0,069	0,03047+0,00006	0,03053 (3)	98,264 32,755
8	Сг6С СгСо. 16667				0,03886 (2)	154,398 25,733
9	Сг3С СгСо,33333				0,03525 (2)	85,107 28,369

ческой Сг₃С₂ с к_ромб = —— (координационное 8

число к_Кч = 6) отвечает объемная структурная постоянная              К_г = к_гпу • к_ромб • к_КЧ =

= 2^.^.6 = 2,38649.

Для ОТР-2 ур. (1) принимает вид: с;1(сгс,)=с;1(сгсо42857)-__х-0,42857 .

^2 [^х2 Ср (с) + Ср (СгС_{0 4285}7 )] с;¹ (СгС,) = 0,03351

__х-0,42857.

2,38649(0,66667-8,554 + 24,838) ’ сДСгС,^ 0,03351-0,01251х.(3)

Результаты расчетов по уравнению (3) приведены в табл. 1 и на рис. 1.

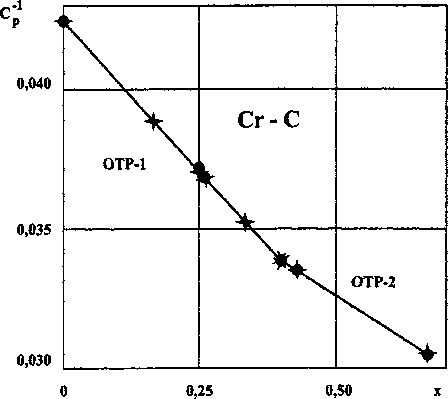
Рис. 1. Зависимость обратной теплоемкости от состава карбидов хрома (• - эксперимент, х - расчет)

Из сравнения расчетных (колонка 6) и справочных (колонка 3) величин С_р карбидов хрома следует их хорошее согласие, не выходящее за пределы доверительных интервалов последних. Расчеты С°(О₅0₂) по уравнениям для ОТР-1 и ОТР-2 согласуются между собой С°(Сг₅О₂) - 147,775 ±0,110. Эта средняя расчетная величина больше справочной на 0,080. В табл. 1 (строки 8, 9) даны величины С_р карбидов, о которых имеются упоминания в литературе, но отсутствуют величины теплоемкостей.

ЭНТРОПИЯ

Математическая модель

• 1.    Энтропия вещества складывается из двух независимых величин: AS_m (от mass), связанной с массой и AS_in (от interaction), определяемой межчастичным взаимодействием.

• 2.    Обратная величина 4S_in бинарного вещества (AS~^) равна сумме обратных величин А8^ компонентов с учетом состава и кристаллических структур. Бинарным является сложное вещество, если в нем можно выделить структурные составляющие. Все расчеты относятся к одному молю металла, то есть состав выражается как МеА_х, энтропия - в Дж-К"¹-моль^-1. Физический смысл величины AS^n^- изменение температуры моля вещества при изменении энтропии взаимодействия на единицу [1].

• 3.    В зависимости от кристаллических структур, определяемых составом и изменяющимся атомно-молекулярным взаимодействием, диаграмма AS^-x делится на области твердых растворов (ОТР). В каждой ОТР выделяется кристаллообразующий компонент (КО) - устойчивое вещество с известной энтропией и структурой. В ОТР-1 кристаллообразующим компонентом всегда является металл.

• 4.    В общем виде расчетное уравнение зависимости А8^ от х выглядит так:

S = AS_m + AS_in. (4)

У частиц в кристаллическом веществе имеется только одна степень свободы поступательного движения (вдоль пути реакции), поэтому

A5_m=|/?lnM,(5) где М - относительная атомная, молекулярная масса; R - универсальная газовая постоянная.

48^ определяется из уравнения (4). В зависимости от условий она может иметь положительное или отрицательное значение, 4S_m - только положительное.

^-ДМеА>88"ДК0^

_± х-х^КО^

к^аМ+^^о)]’ где К - объемная структурная постоянная, количественно характеризующая пространственное расположение взаимодействующих частиц и структурных составляющих. Величина К в каждой ОТР определяется сочетанием структурных компонентов [1], х„ - координата границы рассматриваемой ОТР.

Уравнение (6) можно привести к удобному виду

А$7„ (МеАх ) = a ±Ьх.         (7)

Эта модель была проверена на простых и сложных оксидах [4, 13-15]. Результаты расчетов энтропий стехиометрических и нестехиометрических оксидов согласуются со справочными данными в пределах точности экспериментов.

При образовании соединения АВ_Х из компонентов А и В, находящихся при стандартных условиях в кристаллическом состоянии, между ними возникает конкуренция за место кристаллообразующего компонента. Возможные варианты: А внедряется в В (например, уран в кристаллическую серу) или В в А (сера - в уран). По определению в ОТР-1 кристаллообразующим всегда является металл, поэтому в основном ур. (6) вклад в AS_tn второго компонента учитывается его долей (х), приходящейся на 1 моль металла. В других ОТР учет аналогичен. В этом заключается принципиальное отличие от соединений типа АВ_Х, в которых компонент В при стандартных условиях находится в газообразном состоянии. Однако значительный интерес представляет выяснение пригодности модели для расчета энтропии веществ, в которых компонент А является при стандартных условиях кристаллическим, а не газовым. Это явилось одной из причин выбора в качестве объектов изучения карбидов хрома СгС_х.

В табл. 2 (колонки 1-3) приведены исходные справочные сведения о составе, структуре и энтропии карбидов. Все они являются бертоллидами. Из анализа данных колонки 2 следует, что в системе Сг-С должно быть две ОТР: первая включает соединения с кубической структурой, вторая - с более сложной.

ОТР-1 (х - 0*0,4). КО - Сг

В этой ОТР по мере внедрения углерода происходит переход от структуры ОЦК (Ст) к структуре ГПУ (Сг5С2). Вероятно, это вещество находится на границе между Областями твердых растворов. Для ОЦК структурная константа

^оцк ®^я ГПУ к_гпу - -j=.

Объемная

структурная         постоянная         ОТР-1:

^1 - коцк ‘ кгпу ■ Ккч ~ "^

4=-4 = 1,15470

V3

(координационное число к№=4).

Ур. (6) принимает форму:

Д^ (CrCx) = AS"1 (Сг)-х - 0 "^AS^cJ^AS^j]’ Д5Г1(СгСЛ) = 0,13933

X

1,15470 [-4,594-0,4+7,177]’

Решая уравнение (7), например, относительно Д5_ги(СгС₀₂б087) получим Ь- 0,14484 и уравнение (8) примет вид:

AS"1 (CrCj = 0,13933 -0,14484 х. (9)

Результаты расчетов приведены в табл. 2 и на рис. 2. Расчетные величины хорошо согласуются с экспериментальными. '

Таблица 2

Энтропия карбидов хрома

	Вещество	Структура	S, [9, Ю, Гб]	4Sm, УР- (2)	А8,„, ур.(1)		^гЛ УР-(6, 8)	S, расч.
	1	2	3	4	5	6	7	8
1	С	ГПУ	5,740±0,126	10,334	-4,594
2	Сг	ОЦК (a-Fe)	23,640±0,209	16,426	7,219	0,13853	■ 0,13933	23,603
3	Сг4С СгСо,25	ГЦК-4	105,855 26,464	16,659	9,795	0,10209	0,10312	105,426 26,356
4	Сг23С6 СгСо.26087	ГЦК-4	610,027±2,924 26,523	16,669	9,854	0,10148	0,10167	609,891 26,517
5	Сг5С2 СгСо.4	ГПУ-4	144,766±1,255 28,953	16,793	12,160	0,08224	0,08230	144,720 28,944
6	Сг7Сэ СгСо, 42857	ГПУ-8	202,087±1,255 28,870	16,818	12,052	0,08248	0,08297	202,097 28,871
7 .	Сг3С2 СгСо.66667	ромб.-4	84,935±0,412 28,3117	17,021	11,2907	0,08857	0,08854	84,945 28,315
8	Сг6С СгСо.16667			16,583			0,11519	151,585 25,264
9	Сг3С СгСо,ззззз			16,734			0,09105	83,151 27,717

ОТР-2 (х - 0,4-0.66667). КО - Сг2Сз

В этой области переходу от структуры ГПУ Оглу = ^) ^к ромбической <к_ромб = -^У отвечает объемная структурная постоянная ^2 ⁼ ^гпу ‘ ^ромб. • ^Ккч ~ ~^" ~^ " 6 = 4,24264.

В качестве КО используем Сг₇С₃ как хорошо изученный. Ур. (6) примет вид:

^/V (CrC_x^ - AS^¹ (CrC₀₄₂857) +

__________X- 0,42857.

K2[x2AS,„(C) + AS„(CrC0,4285?)]

AS",(CrCx) = 0,08297 +

+_____r -M28L7

4,24264 [-4,594 ■ 0,66667 + 7,177]

Используя данные по Сг₃С₂, получим b = 0,02338. Уравнение (10) преобразуется:

AS71 (СгСх) = 0,07295 - 0,02338%.(11)

Вычисленные значения AS”1 и 5 помещены в табл. 2 и на рис. 2. Согласие расчетов и экспериментов хорошее.

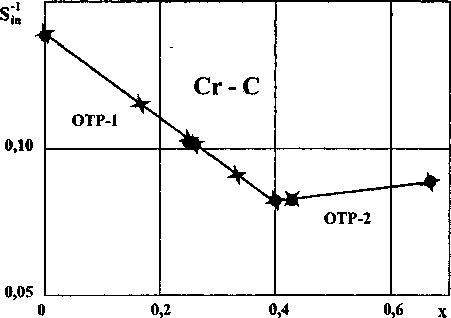
Рис. 2. Зависимость обратной энтропии взаимодействия карбидов хрома (СгСх) от состава (• - эксперимент, х - расчет)

Совместное решение уравнений (9) и (11) дает х 0,395, что практически совпадает с х = 0,4 (различие 1,25%). Этому соответствует S(Cr₅C₂) = 144,810, отличающееся от рассчитанного по ур. (11) на 0,090.

Полученные результаты подтверждают возможность использования разработанной модели для расчетов энтропии бинарных соединений, в частности, карбидов.

Выводы

• 1.    Разработаны математические модели расчетов стандартной теплоемкости и энтропии бинарных кристаллических соединений металлов, содержащих компоненты, являющиеся кристаллическими в стандартных условиях.

• 2.    Адекватность модели справочным данным подтверждена расчетами теплоемкости и энтропии карбидов хрома.

• 3.    Математические уравнения модели позволяют рассчитать С® и 5° карбидов хрома произвольного состава, что особенно важно для соединений с малым содержанием углерода.

• 4.    Модель обладает предсказательностью.

• 5.    Обоснована возможность использования модели для расчета С_р и S⁰ бинарных кристаллических соединений типа МеА_ы где А - В, Si, Р, S, Ge, As, Sb, Bi, существующих при стандартных условиях в кристаллическом состоянии, что особенно важно для теории и практики легирования низкоуглеродистых сталей и сплавов.