Старение сплавов как multiscale-эффект в рамках теории нанокомпозитов

ВЕСТНИК ПНИПУ. МЕХАНИКА № 6, 2023PNRPU MECHANICS BULLETIN

Бурное развитие градиентных теорий [1–4], начавшееся в конце прошлого века [5-8], привело к осознанию того факта, что механика объектов с размерами от сотен микрон до десятков нанометров принципиально отличается как от классической механики, так и от квантовой [9; 10]. Новая механика – наномеханика – отличается от классической наличием multiscale-эффектов, а от квантовой – детерминированной постановкой. Одним из первых достижений теории нанокомпозитов, построенной на наномеханике многофазных сред, является объяснение аномального усиления эффективного модуля Юнга стержня, изготовленного из мелкодисперсного композита: при постоянной относительной объёмной доле армирующих частиц эффективный модуль растет при уменьшении абсолютного размера армирующих частиц [11]. Аналогичные multiscale-эффекты были установлены [12; 13] и объяснены [14–16] для волокнистых нанокомпозитов и композитов, армированных нанотрубками. Эти multiscale-эффекты послужили толчком к объяснению эффекта старения сталей и сплавов. С другой стороны, толчком к этой идее послужила проблема агломерации армирующих частиц на этапе хранения или изготовления нанокомпозита. Действительно, пока адгезионные взаимодействия в агломерации не превышают предела адгезионной прочности, агломерация ведет себя как большая частица с теми же свойствами, что и исходные. Единственное различие – абсолютный размер. При хранении наночастиц используют различные ПАВы, снижающие адгезионные свойства наночастиц и препятствующие их агломерации. Для уже изготовленного нанокомпозита применяются, как правило, соответствующие режимы термообработки, приводящие к распаду агломераций на мелкие части и последующей их диффузией. Если обратить во времени это явление, то полученный процесс можно воспринимать как модель старения: изолированные наночастицы армирующей фазы диффундируют и объединяются в агломерации, снижая тем самым эффективный модуль дисперсного нанокомпозита. Так как оба процесса – и распад, и агломерация – зависят от технологии термообработки, будем в дальнейшем оба процесса называть моделями старения.

Материалы и методы

Любая градиентная теория наиболее просто формулируется в соответствии с принципом Лагранжа. Вариационный принцип Лагранжа сводится к требованию стационарности функционала Лагранжа L , который формулируется как разность работы внешних сил A и потенциальной энергии U .

Вариационная постановка

Лагранжиан градиентной теории упругости:

L = A - U,

A = J P^RdV + J p F RdF,                 (1)

VF jmn m,n ,j jkmnl m,nl ,jk ,

2V где PiV – внешние объёмные силы; PiF – поверхностные силы; Ri – вектор перемещений; Cijmn – тензор четвертого ранга классических модулей упругости, Cijkmnl – тензор шестого ранга неклассических модулей упругости.

Рассмотрим для простоты так называемую биплос-кую 1D-постановку. Назовем биплоской такую постановку, в которой искомый вектор перемещений имеет единственную (осевую) компоненту R i = R ( x , y , z ) X_t , где X_i – орт направления, совпадающего с осью двухфазного композиционного стержня. Будем называть 1D-по-становкой такую, в которой искомые функции зависят только от одной координаты (в данном случае – от координаты x ). Таким образом, биплоская 1D-постановка определяет искомый вектор перемещений следующим образом:

R i = R ( x ) X,.                      (2)

Различные градиентные теории отличаются структурой тензора модулей шестого ранга C_ijkmnl .

Биплоская 1D-постановка приводит любую градиентную теорию к одному и тому же лагранжиану [17–20]. Действительно, дадим следующие определения:

С XXX X = E, ijmn i j m n ^,

C^ ni X.X j X k X m X n X i = El 2 , P X = 0, P F X, = °.

Подставляя (2) в (1), с учетом определений (3), лагранжиан градиентной теории упругости приобретает вид:

x ₂

L = PFR | x ² - 2 J ( ER'R' + El ² R"R")Fdx ,       (4)

где x ₁, x ₂ – соответственно координаты левого и правого конца составного стержня, являющегося ячейкой периодичности композитного стержня с постоянной площадью поперечного сечения F , о - растягивающая внешняя поверхностная нагрузка на торцах.

Вариационное уравнение, вытекающее из требования стационарности лагранжиана (4):

5L = [ (EFR" - EFl2R")5Rdx + x1

+ [о F - EF ( R' - 1 ² R ^m)]5 R | x - EFl ² R "5 R' | x 2 = 0.

Уравнения равновесия для двухфазного композита:

R"-1I2 R " = 0,(6a)

R"-l2R " = 0.(6b)

Здесь индекс I, II нумерует первую и вторую фазу соответственно. Этими индексами наделяются параметры фаз E , l , x – соответственно, модули Юнга, характерные длины когезионных взаимодействий в фазах и абсолютные объёмные доли фаз. Для определенности будем считать первую фазу армирующей, а вторую фазу – матрицей.

Решение для обеих фаз.

Первая фаза:

RI(x) = A0 + Д (x - x1) + A3sh((x - x1)/11).(7a)

Вторая фаза:

R II (x) = B0 + B1 ( x - x 2) + B3 sh ((x - x 2) /1II).(7b)

Контактные и граничные условия.

Граничные условия при x = x 1 :

; E i[ R ‘(0) -112 R ‘(0)] = о,

_ E I 1 I ² R I" (0) = 0.

Граничные условия при x = x ₂ :

/ En[Rn( x 2) -12R "(x 2)] = O,

\ E 11 1 X( x 2 ) = 0.

Контактные условия при x = x_c , где x_c - координата точки контакта фаз x 1 <  x c <  x ₂:

R i ( x_c ) = R _n( x_c ), R | ( x_c ) = R |i ( x_c ),

‘ E i [ R | ( x c ) - 1 1 ² R Д x c )] = E _n[ R |i ( x c ) - 1 i²i R "'( x c )], _ E 1 1 1 ² R i"( x c ) = E II 1 ²i R ;I( x c ).

Определим абсолютные доли фаз следующими соотношениями:

x I = x c - x ! , ^x II = ^x 2 ^- x c .

Решение (6) с учетом граничных (8), (9) и контактных (10) условий:

^R I ⁽ x ) = ^B 0 ^{- O}

⁽ x I ^{+ 1}f )   ⁽ x II ^{- 1}f )

E I          E II

о

+ — ^{( x -} x ! ) + ¹

^E i L

R _n( x ) = B 0 + -°-

E

+

sh (( x - x j )/ 1 1 ) sh ( x _I/ l _I)

( x - x 2 ) + 1 f

sh (( x ₂ - x )/ 1 II ) sh ( x _II / l _II)

Здесь дано определение характерной длины межфазного слоя l_f , определяющей multiscale-эффект:

-

¹f =

E _II    E _I

E _I l _I th ( x _I / l _I)    E _II l _II th ( x _II/ l _II)

Нетрудно убедиться, что при стремлении неклассических параметров l _г и l_п к нулю характерная длина межфазного слоя стремится к нулю l f ^ 0 .

Потенциальная энергия нанокомпозита по теореме Клапейрона:

U = о[ R _п( x ₂) - R _t( x ^/2 =

^{( x} i + ^lf )   ^{( x} ii ^{- l}f )

E i    ⁺   E ii

/2.

Потенциальные энергии классического (при l f ^ 0) и нанокомпозита:

1 X, / l x tt / l — = -— + ——, E E i E _п

1 ( x i + l f )/ 1 ( x ii - l f )/ 1 — =----- ^f ----+------ ^f ----. ^{E      E} i           ^E ii

Отметим принципиальную разницу соотношений (15a) и (15b).

Эффективный модуль классического дисперсного композита не зависит от абсолютного размера частиц армирующей фазы. Действительно, если переписать (15a) через относительную объёмную долю ф , получим классическую формулу осреднения по Рейссу, правая часть которой не зависит от абсолютного размера армирующих частиц:

композита

(15a)

(15b)

£ = ф + ^{(1 -} ф) E E i    E _п

Эффективный модуль нанокомпозита зависит от абсолютного размера частиц армирующей фазы. Действительно, если переписать (15b) через эффективную относительную объёмную долю ф * = ф + lf / 1 , получим неклассическую формулу осреднения по так называемой гипотезе эквивалентного континуума, в которой эффективная относительная объёмная доля является функцией абсолютного размера армирующих частиц x _i через l_f в соответствии с (13).

Изменение модуля нанокомпозита как функции характерного размера армирующей фазы

Отметим, что при распаде или при агломерации армирующей фазы её относительная объёмная доля ф не изменяется. Изменяется только размер ячейки периодичности l , тогда в соответствии с (11):

x i = ф l, xii = (1 - ф)l.

Из (16) видно, что абсолютные доли фаз xi,xii и длина (объём) ячейки периодичности l пропорциональны друг другу. Поэтому для сохранения симметрии относительно фаз будем считать управляющим параметром не xi, а l - длину ячейки периодичности.

Приращение модуля Юнга нанокомпозита:

7 I 1         1 I dE = E2---d(l, /1). f

V E ii    E i )

В соответствии с (13) вычислим ( l_f / 1 ) как функцию l :

( l f / l ) =

1Eii -1Ei r   th (ф l / lt)

E, ф ——--—

(ф l / 1 1 )

. (18)

E _n(1 - ф)

th ((1 - ф) l / 1 _ii) ((1 - ф) l / 1 ii )

d ( l_f / 1 )

В соответствии с (18) вычислим —:---, а затем dl в соответствии с (17) производную dE dl '

dE

"dl"      ^{( El}f / ^l )

sh (2ф l / 1 , ) - 1     sh (2(1 - ф) l / 1 _п) - 1

(2ф l / 1 a       ₊ (2(1 - ф) l / 1 _n)

sh ²(ф l / 1 а   _Р. sh ²((1 - ф) l / 1 _n)

El E l н (фl/1а       ,,п ((1 -ф)l/1n)

Теорема 1. При фиксированной объёмной долерас-пад армирующей фазы приводит к росту эффективного модуля Юнга нанокомпозита.

Доказательство. При фиксированной относительной объёмной доле армирующей фазы распад армирующей фазы определяется тем, что размер ячейки периодичности будет уменьшаться:

dl <  0.

Как следствие, из модели старения (19) можно вывести, что эффективный модуль Юнга будет возрастать:

dE >  0.

Теорема 1 доказана.

Теорема 2. При фиксированной объёмной доле агломерация армирующей фазы приводит к снижению эффективного модуля Юнга нанокомпозита.

Доказательство. При фиксированной относительной объёмной доле армирующей фазы агломерация армирующей фазы определяется тем, что размер ячейки периодичности будет увеличиваться:

dl >  0

Как следствие, из модели старения можно вывести, что эффективный модуль Юнга при этом будет снижаться:

dE <  0 .

Теорема 2 доказана.

Таким образом, на основании (19) доказано, что для любой модели градиентной среды (т.е. для любой структуры тензора модулей шестого ранга в соответствии с (3)) эффективный модуль нанокомпозита является убывающей функцией абсолютного размера армирующей фазы. При этом в соответствии с (15) и (16) эффективный модуль нанокомпозита асимптотически стремится к эффективному модулю классической теории. В соответствии с (15), (16) и (18) эффективный модуль нанокомпозита является функцией пяти параметров: E = E (Ei, Eii, ф,(ф 1 /1i),(1 - ф) 1 /1ii).

Введем обозначения:

E *

( E ,

2 E _п/1 1 + ¹ I

I k J

¹ 1 / L = 1 *

2 II

Тогда (21) приобретает вид:

¹ = ф ₊ ⁽i ^- ф) EE I E II

^^^^^e

(— - — ) 2

EII   EI th(ф 1 /1i) +            th((1 -ф) 1 /1 ii)

E l ф E l (1  ф)

(ф 1 / 1 i ) ^iiv ((1 - ф) 1 / 1 ii )

(20) ^,

E * =---------¹--------Г.

1 - th ( 1 * ) Г k - 1 Y

1 * I k + 1 J

1 ф (1 - ф) lim— = +-—— i — o В E, E

^^^^^^»

(— - —)2

E II    E I

,

Если модуль армирующей фазы гораздо больше мо дуля матрицы, то множитель (k -1)k +1)2 можно считать

равным единице. На рисунке построена кривая

E * = E * ( 1 * ) для этого случая.

L E i ф   E _П(1 - ф) J

E II E

1 ф (1 - ф) lim— = —+ -——, ¹ ^ E E i E ii

= ^{ф+(1 -} ф) k

-

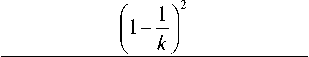
th (ф 1 / 1 i )⁺ th ((1 - ф) 1 / 1 ii ) ^{k ф} (ф 1 / 1 i )    ^{(1 -ф)} ((1 - ф) 1 / 1 ii )

ф = 0,5 ——

1 -

E 111        ( k J

—- =--+----—----------

E 2 k 2   1 1

k 1 th ( 1 /2 1 _i) ⁺1 th ( 1 /2 1 _ii)

2( l /2 l _I) 2( l /2 l _II)

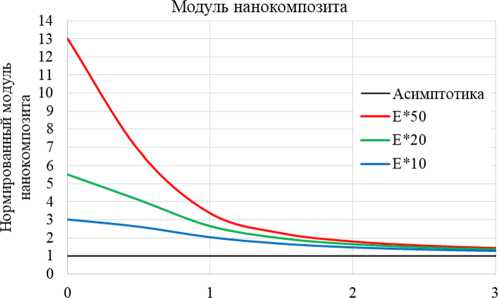
Нормированная длина ячейки периодичности

Рис. Красная кривая для k = 50, зеленая кривая для k = 20, синяя кривая для k = 10

2 E II

| 1 +11

( k J , th ( 1 /2 1, ,) Г k - 1 ) ² = 1 —

E              ( 1 /2 1 _ii) ( k + 1 J

Fig. Red curve for k = 50, green curve for k = 20, blue curve for k = 10

E

2 E / 1 ¹ + 1 ⁱⁱ I k

1 th ( 1 /2 1 _ii) Г k - 1 \ ( 1 /2 1 _ii) I k + 1 )

Чтобы представить (20) в виде пучка «плоских» кривых, необходимо задать три параметра или три связи между параметрами. Пусть модуль армирующей фазы в k раз больше модуля матрицы E _i = kE _ii, а относительная объёмная доля армирующей фазыф = 0,5. В качестве третьей связи выберем следующую:

¹ 1 = ¹ ii .

Тогда (20) приобретёт вид:

E 1

2 E„ / 1 1 + ^{1 ii} I k

1 +

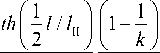
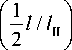
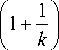
Заключение

На основании теории мелкодисперсных нанокомпозитов (14), (15b) получена зависимость производной эффективного модуля Юнга от абсолютного размера армирующих частиц (19). Рассмотрены два случая. Первый – распад армирующей фазы. В этом случае эффективный модуль нанокомпозита возрастает. Второй – агломерация частиц армирующей фазы. В этом случае эффективный модуль нанокомпозита снижается. Эти закономерности представляются универсальными.

Однако следует обратить внимание, что остается открытым вопрос о том, что наряду с градиентным обобщением возможно нелинейное обобщение. Действительно, в отличие от керамик, сохраняющих физическую линейность практически до разрушения, металлокомпозиты проявляют пластичность на достаточно большом интервале деформаций. Однако обобщение на физически нелинейный случай, а тем более – на пластичность, осложняется тем, что до

настоящего времени не существует общепринятой теории построения кривой напряжение – деформация даже для однородных материалов. Таким образом, моделирование