Статические характеристики и методы расчета установившихся режимов работы синхронных двигателей

При расчетах и оптимизации установившихся режимов систем электроснабжения промышленных предприятий со значительной установленной мощностью синхронных двигателей (СД) необходимы, в ч и с л е прочих, аналитические описания связей вида:

gi(Pi,Q,U1,l1) = 0, g2(Pi.Q.Ui.i2) = °.                                                                 (2)

_5з(в₁,и,л₁) = о,                                                                (3)

где g 1, g2, g3 - неявные функции; P 1,Q - активная, кВт и реактивная, кВАр, мощности СД; U1,11 -напряжение, кВ, и ток, А, статора; 12 - ток возбуждения, А; Q, I2 - нижние предельно допусти-к мые значения реактивной мощности и тока возбуждения из условия осуществимости установившегося режима работы СД.

Статические характеристики СД и методы расчета их установившихся режимов работы (зависимости Q , I 1 при заданных P 1 , U 1 , I 2 и зависимости Q , I 2 при заданных P 1 , U 1 ) должны учитывать явнополюсность ротора и изменение насыщения магнитной цепи и использовать минимальное количество исходных данных.

Аналитические описания и методы расчета. Используя результаты работ автора [1], аналитическое описание нормальной характеристики холостого хода СД, предложенное Ю.М. Голодновым [2], и следующие обозначения:

-1 R = 5 1

“^х S_H’   ^s V

и₁ ~^-7Г-^и 1н

21,

£ 2

^ 2

/ 2н ,

нетрудно показать, что искомые связи (1), (2) могут быть описаны следующими нелинейными уравнениями:

д1=«^в^иМ5=0,(5)

g2 = L(i2)-*(«s,es,u) = 0,(6)

L(z2) = е2 = £2н •/г, (7) *(a„fc.«) = Ei = r + №Er + 2.E.4e.co,(6-5,), (8) i Е = -• Fd • fc • sin6 + (w2 + xd • ax) • cos6], (9) 0514.^11-. Д£ i-0.57^ I0,15 £P + (0,13 £P 0,0514 £P)J £P, (10) u2+xp-as £P = u-cosV (11) о        „X

6 = arctan—г-2----,(12)

Р            y?+xp•as , где Sн – номинальное значение полной мощности СД, кВА; U1н, I1н – номинальные значения напряжения, кВ, и тока статора, А; 12н - номинальное значение тока возбуждения, А; е0, е — относительные значения электродвижущей силы (ЭДС) возбуждения с учетом и без учета насыщения магнитной цепи; ε0н – номинальное значение ЭДС ε0; εp – относительное значение ЭДС Потье; Δε – относительное значение ЭДС Кимбарка; θ – угол между ЭДС ε и напряжением статора, рад.; 6p - угол между ЭДС еp и напряжением статора, рад.; xd, xq - синхронные индуктивные сопротивления СД по продольной и поперечной осям, отн. ед.; xp - индуктивное сопротивление Потье, отн. ед.

Задача расчета установившегося режима работы СД на основе полученных математических зависимостей заключается в том, чтобы для заданных относительных значений активной мощности в s , напряжения статора и и тока возбуждения I ₂ найти относительные значения реактивной мощности α s и тока статора I 1 . Для решения задачи необходимы следующие исходные данные о СД: cos φ _н , x _d , x _q , x _p , где cos φ _н – номинальное значение коэффициента мощности. Метод решения задачи сводится к следующему:

• 1)    принимают

ах = sin фн, ps = cos фн, и = 1

и по (12), (13) рассчитывают углы δ p , θ , затем по (9), (10), (11) – ЭДС ε p , Δ ε , ε и по (8) – квадрат номинального значения ЭДС возбуждения е_р = е_Рн ;

• 2)    принимают значение β s , u , I 2 равными заданным и, решив уравнение (6) с учетом (7) – (13), находят искомое значение α _s ;

• 3)    подставив заданные значения β s , u и найденное значение α s в (5), вычисляют искомое значение I

Корни уравнения (6) находят как абсциссы точек пересечения кривой ψ(αs, βs, u) с прямой L(12) (рис. 1а). Точка касания прямой L(12) с кривой ф(as, вs, и) определит нижнее предельно допустимое – из условия осуществимости установившегося режима – относительное значение реактивной мощности as = as (рис. 1б). Множеству значений {as = as < as < 0} отвечает режим работы СД с отстающим cos ф, значениию as = 0 - режим работы с cos ф = 1,0 и множеству s значений {as : as > 0} - режим работы с опережающим cos ф.

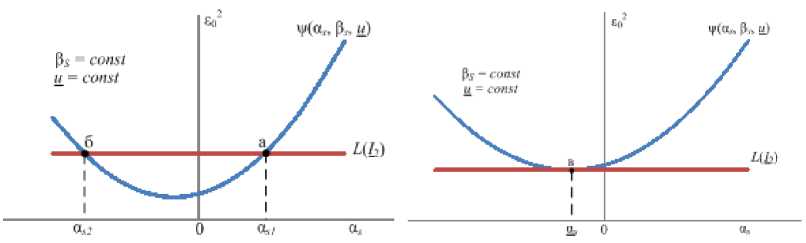
а)                                       б)

Рис. 1. Определение корней нелинейного уравнения (6) и предельно допустимого относительного значения реактивной мощности по условию осуществимости установившегося режима СД

Для получения математических зависимостей, описывающих связь (3), достаточно взять производную функцию ψ ( α s , β s , u ) по α s и приравнять полученное выражение нулю:

Эф(а5,р5,и)

У з =   —— = е • ^ + Де • ^ + 2 • Де • ^ з +

Эи5

+(е • ^2 + Де • ^1) • cos(0 - бр) = 0,

^i = - • (xd • cos3 6 + ^ДДД^г • sin3 б),

«P

*-^-fe^-K« p +(p-0^^

⁺ 1 - 0,57 • Е_р

0,13 - 0,1028 • Ер ^0,15+---------------------^р---- г

2 • (0,13 • Е_р - 0,0514 • Е р )⁵

‘1

,

где е , А е , е р , 0, 8 p = f(a s , в s , и ) (см. выражения (9) - (13)).

Метод расчета нижних предельно допустимых значений реактивной мощности и тока возбуждения из условия осуществимости установившегося режима сводится к следующему:

• 1)    принимают значение β _s , u равными заданным и, решив уравнение (14) с учетом (15) – (17), (8) - (13), находят искомое значение a s = a s ;

• 2)    подставив заданные значения в s , и и найденное значение a _s в (8) - (13), по (12), (13) рассчитывают углы 8 _р , 0 и по (9) - (11) - ЭДС е , А е , е _р ; далее по (8) вычисляют квадрат ЭДС е_р и по (7) - искомое значение - , =- , .

Если допустим, что

Xq = Xd,AE = 0, т.е. не учитывать явнополюсность ротора и изменение насыщения магнитной цепи, то уравнение (6), как нетрудно показать, примет вид х^ + 2^а^-^ = ° а уравнение (14) – вид xd • ах + и2 = 0, где eн = x^ + 2•xd•sinфн + 1.

Из (18) (19) ..,                      2, "’      ^н“

«, = «, = -!(

Подставив в (18) вместо α s его значение из (22), имеем:

h=h=^ .                                             (23)

Найденные по формулам (21), (22) значения a _s и a _s можно использовать в качестве начальных приближенных оценок корней уравнений (6) и (14).

Учитывая дифференцируемость функций g 2 и g 3 и возможность выбора по (21), (22) начального приближения, целесообразно при поиске корней нелинейных уравнений (6) и (14) использовать итерационный метод Ньютона.

Расчет установившихся режимов работы синхронного двигателя. Используя математические зависимости (5) - (17) и приближенные формулы (21) - (22), выполним расчеты установившихся режимов работы синхронного двигателя со следующими исходными данными:

cos ф_н = 0,9, x_d = 0,673, х_ч = 0,448, х_р = 0,125.

Результаты расчетов в виде графиков зависимостей a = f(12), a = f(u), 11 = f(12), a = f(u), i2 = fU)) для случая β = 0,72, где а = Q = а р= Р1 = р$

“ ^Qh sin^ H ,    ? 1н cosV H

P 1н , Q н – номинальные значения активной (кВт) и реактивной (кВАр) мощности СД (рис. 2-6).

Для сравнения здесь же приведены значения α , I ₁ полученные экспериментально.

На рис. 2–6 приняты следующие условные обозначения:

– графики, полученные по выражениям (5) – (17);

– графики, полученные по выражениям (21) – (23);

*   – значение α или I ₁ , полученное экспериментально.

На рис. 2–6 видно следующее:

• 1)    использование взамен приближенных формул (21) – (23) математических зависимостей (5) – (17) существенно повышает точность расчетов установившихся режимов работы СД;

• 2)    различия в значениях a и 1 1 , полученных экспериментально и с использованием математических зависимостей (5) – (13), незначительны, т.е. последние достаточно точны и могут быть применены при расчетах и оптимизации установившихся режимов систем электроснабжения промышленных предприятий.

  

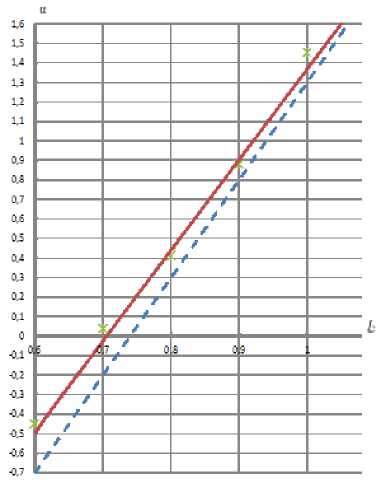
  Рис. 2. График зависимости а = f ( 1 2 ) для и = 0,95

  
  
  

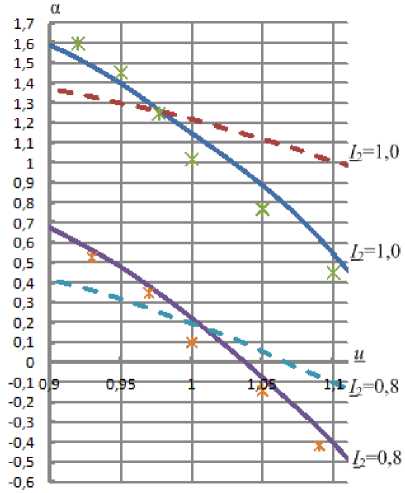
  Рис. 3. Графики зависимости а = f(и ) для 1 _г = 1,0 и 1 2 = 0,8

  
  
  

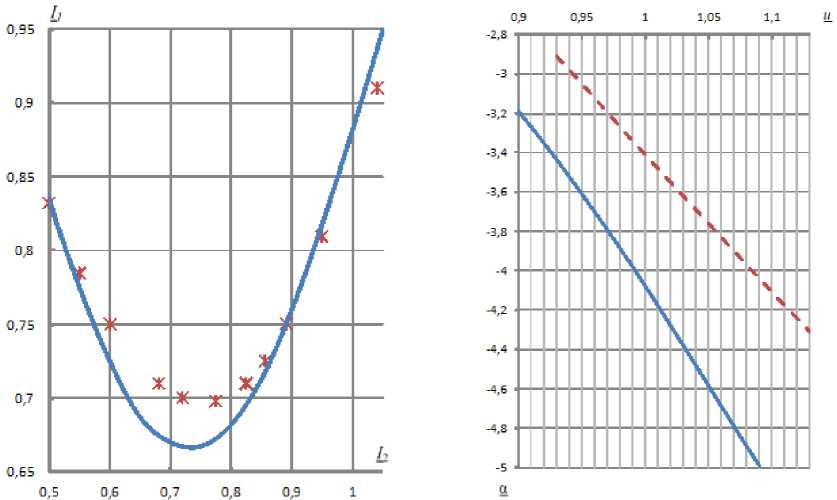
  Рис. 4. Графики зависимости 1 1 = f ( 1 2 ) для и = 0975

  
  

  Рис. 5. Графики зависимости а = fЦ) )

  
  

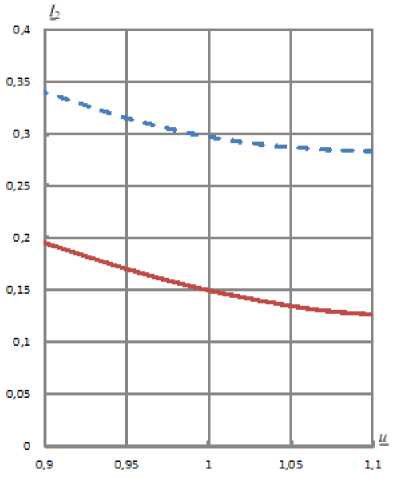
Рис. 6. Графики зависимости / 2 = f (u )