Statistical analysis on result prediction in chess

Published Online July 2018 in MECS

Chess Engines with ever increasing high computational power can now evaluate moves to more depth in less time. However, most of the initial moves and opening combinations have already been played since the invention of Chess. With more than 9.3 million chess games data available [1], we can make Chess Engines learn from the previously played games and the game outcomes, thereby increasing its efficiency wherever needed as per the capacity of underlying hardware and computing resource. Board evaluations for each halfmove have been done with a depth of 17 for all games. This much depth would take only few seconds in calculating board evaluations on most of the personal computers while winning scores could be fetched using past data. The depth can be adjusted according to the computational power of the computer. This produces the value of parameters for our algorithm faster and hence, the final decision factor is generated immediately without going deep into the search tree. Our approach for predicting the game winning probabilities is based on generating a linear relation between the taken response variable of game result and different set of predictor variables like evaluation and winning score of moves. Decision for playing which of the possible next moves could be made faster in Versus Computer games especially in fast modes like Bullet Chess.

Using different attributes related to a particular game, for example move sequence, move number, game result, opening move classification, half-moves played by white or black and the corresponding engine evaluations, a set of relations between these could be developed. Using the classification and statistical relationship among attributes, a sequence of best opening moves can be classified for both white and black. These relations could help chess players and engines to develop more winning strategies accordingly.

We have used 10,000 annotated games in Portable Game Notation (PGN) format and created three different datasets of 10-moves, 15-moves and 20-moves to analyse the effect of increasing the number of moves considered in each game on accuracy and relationship.

The regression model indicates a high dependency of past game outcomes on result prediction. Board evaluations doesn’t seem to be playing a major role in predicting the game outcomes while move sequence number becomes a fair predictor variable whenever used. Thus, past data can play a significant role in suggesting moves and could be incorporated in chess playing and statistical tools. The classification model provided the highest accuracy of 66.91% when two attributes namely opening sequence and winning score are considered in the 20-moves dataset. The evaluation scores didn’t affect the accuracies much here as well. Since the winning score variable comes to be a significant predictor, we used winning score as the deciding factor for initial moves with frequency threshold of 10 games and played 20 versus-computer games being on each side. After the threshold, the games were made to be finished by the same engine on both sides.

Section II describes the current research work done on similar approaches; basics and nomenclature of chess so that the reader could relate with the terminology used in the text; and the brief description of the tools used by the authors. Section III explains the project implementation in sequential order of usage. It also explains the usage of dataset, engine evaluation score, text-processing and then the implementation of machine learning algorithms over the dataset. The Section IV mentions about the generated results and their implication with the project. Section V presents the conclusion of our current research work.

• II.    Related Works

This section discusses about the related works and background study the authors have referred to before and during the project. Additionally, this section includes basics and nomenclature regarding chess and the software and hardware tools used by the authors to evaluate and generate results.

• A.    Research Work

  Garry Kasparov, former World Chess Champion, mentions in [2] that there are 1040 number of legal chess positions while the number of different possible games is 10120. As described in [3], the possible chess positions after white’s first move is only 20 while it grows to 400 after black’s first move. After just 6 moves, there are 91,32,484 total possible board positions. Thus, it’s not practically possible to make any chess tool learn about the results of every possible combination of chess games. This makes chess a great domain of research for Artificial Intelligence (AI) and Machine Learning.

As described in Section I, the proposed algorithm is rather a very general implementation while there have been plenty of research work done on similar approaches.

In [4], NeuroChess learns to play chess from the final outcomes of games using temporal difference learning [5], inductive neural network and a neural network version of explanation-based learning [6]. The model is trained using a database of 1,20,000 expert games before making NeuroChess learn an evaluation function. On using the same search engine NeuroChess won approximately 13% of all games against GNU-Chess [7], however, it still played incredibly poor openings which are usually responsible for a lower positional or tactical benefit for future moves. While discovering a great research direction for chess, the author also mentions that the level of play still compares poorly to GNU-Chess and human chess players and that NeuroChess still faces problems like limitation of training time. It spends most of its time computing board evaluations. Another machine learning technique, reinforcement learning, is used in [8] on the results of high-level database games.

The huge chess database available online [1] provided us with a considerable fraction of possible and legal expert games and this could be made a huge dataset for learning algorithms. Hence, we have also referred to different approaches to predict moves that use past data of chess games. A three-layer Convolutional Neural Network (CNN) in [9] is used to make predictions using 20,000 games from Free Internet Chess Server. In chess frame, search space tree of chess increases exponentially with progression in game which make chess engine to take more time for board evaluations on same depths. CNN reduced the intractable class space in chess by square root by breaking down the task in a piece-selector CNN and a move-selector CNN. Using 8:2 training to validation ratio, the piece selector network produced 38.3% accuracy while the move-selector network performed at 52.20%, 29.25%, 56.15%, 40.54%, 26.52% and 47.29% for the pawn, rook, knight, bishop, queen, and king respectively. The model was played against Sunfish Chess Engine drawing 26% games. Author mentions that the model is adept at characterizing shortterm piece captures.

Playing the game of chess has two broad approaches namely tactical and positional game-play. The former one is based on employing tactics based on short-term opportunities which is generally an open board gameplay in chess and is mainly employed by chess engines by searching game trees to depths typically between 20 and 30 moves with move variations. Positional play, usually a closed game in chess, requires judgement more than calculations and human play is a combination of both since humans have some intuition about better board positions too. A proposed supervised machine learning technique in [10] used a total of 10,75,137 board positions from 6200 games to model the board as network of interacting pieces. The learning was made to identity elements of positional play and predict game outcomes which could be incorporated in chess engines to improve their performance. The results depict the classification accuracy to be better than the engine baseline for low evaluation scores, x, with the intercepting occurring on x = 0.35. This demonstrated that engine might lack important positional insights and that there is a great scope for AI in chess engines.

Most of the previous research work is based on making a program learn chess and thus, building a chess playing tool whereas our main focus lies on predicting values in interest of a human player or incorporating this in addition to the existing chess engines.

• B.    Chess – Basics & Nomeclature

Chess is a two-player strategy board game played on an 8x8 grid chessboard [11] initially having a total of 16 pieces of 6 types on each side. A ply refers to one turn taken by one of the players and is referred as a half-move in chess.

There are several types of chess notations [12] to record and describe moves and related game data. Among these, algebraic chess notation [13] is widely used. It is now a standard notation recognized by World Chess Federation (FIDE) as mentioned by the federation in [14]. It is based on a system of coordinates to uniquely identify each square on the board. The pieces other than pawns are named as K, Q, R, B, and N for king, queen, rook, bishop and knight respectively. The moves are represented by the piece notation concatenated with the coordinate of destination square. The vertical squares or files from white’s left are labelled a through h while the horizontal rows of ranks are numbered 1 to 8 starting from white’s side. Thus, for example, Nf3 indicates a move by knight to square f3. The captures are indicated by an ‘x’ inserted immediately before the destination square, for example, in Bxf3. If there are more than one identical piece which can move to the same square, the moving piece is identified by the inserting file of departure, rank of departure or both in descending order of preference and depending upon the situation, for example, in Ngf3 which indicates that the knight on file g is moved to f3. Castling is indicated by using uppercase letter O as O-O for kingside and O-O-O for queenside. Checks are depicted by ‘+’ appended after the move notation. End of the game or result is indicated by 1-0 for white win, 0-1 for black win and ½-½ for a draw. Sequence of moves with annotations like evaluation scores or comments are written with move numbers for white and followed by ellipsis (…) for black while the comments and annotations are enclosed in braces, for example, in the notation 1. e4 {King’s opening} 1. … e5. Chess games are often stored in computer files using Portable Game Notations (PGN) which uses the same algebraic notation with additional markings and this plain-text format is computer-processible and supported by many chess programs. Refer to [15] for an example of a game recorded using PGN format. Annotation symbols [16] like ‘??’ for blunder, ‘?’ for mistake, ‘?!’ for dubious move, ‘!?’ for interesting move, ‘!’ for good move and ‘!!’ for brilliant move may be used while annotating a PGN file.

Elo rating system is widely used in chess to calculate an estimate of strength of a player [17,18] and is adopted by FIDE. The rating ranges from 2500+ is for most of the Grandmasters (GM) and World Champions, 2400-2500 for International Masters (IM), 2200-2400 for FIDE Masters (FM) and Candidate Masters (CM), 1200-2000 for Class D/C/B/A players while rating below 1200 is for novices.

C. Tools Used

For extracting and processing chess games, we used Shane’s Chess Information Database (SCID) by Shane Hudson [19] on Windows, which is an open source multiplatform application, written in Tcl/Tk and C++, for analyzing huge databases of chess games. While we have imported the Example.si4 database of 1,27,811 games from ScidBase, we have used a newer tool based on it, Steven Atkinson’s SCID vs. PC [20], which has improved interface and additional features like capability to run engine on pre-defined depth or time.

Analysis and annotations are done using Universal Chess Interface (UCI) based Stockfish [21], which is the strongest open source chess engine and is among the top engines ever. Chess engine performance is directly dependent upon system specifications on which it is running, so we used an ASUS ROG G751JY [22] gaming laptop having 24 GB RAM, Intel Core i7-4710HQ CPU and NVIDIA GeForce GTX 980M GPU which was made running continuously with little cool-up breaks for more than a week on Stockfish.

AutoIt v3 [23], a freeware BASIC-like scripting language for windows automation, is used to stimulate few keystrokes over SCID wherever needed for the development phase only and is not used in the final implementation code.

Notepad++ [24] and Bash Scripting [25] with sed [26] are used for text-processing. The output of Stockfish is converted from PGN format to text one and then is streamlined and organized for further processing. For example, each line of the output is made to consist of no more than one half-move and at least one evaluation score should follow the corresponding move in the same line. Every line in the output is also made to end with a carriage return followed by a line feed in order to process the file line-by-line [27, 28, 29].

Python [30], an open-source high-level powerful language, is used to extract data elements from the text file and write it to an excel sheet using the xlsxwriter library [31]. Another GNU project, R language [32] is used to implement machine learning techniques like Linear Regression and Naïve Bayes and to generate corresponding tables and graphs. The bar graphs are generated using Excel. Excel is also used to perform few calculations on the datasets and derive more attributes to be used accordingly.

• III.    Our Project

This section elaborates the process of generating the dataset and then calculating corresponding results in sequential manner. Authors have extracted the PGN data from SCID along with board evaluations with Stockfish engine. Then the dataset is parsed using Python and parameters are collected in an Excel sheet. Finally, the mentioned Machine Learning algorithms are applied over the dataset and results are produced.

• A.    Dataset

We have used the first 10,000 games in the SCID ScidBase Example.si4 database. The games are purely random with no filters or sorting applied. Filtered database like a specific rating range, player or opening could also be applied before fetching for generating condition-based statistics. In our case, the randomly selected games produced variation of moves and game related attributes in the dataset and hence would provide an “overall picture” when fed to machine learning algorithms. Considering the number of games and the total number of half-moves played in each of them summed up give us 8,40,289 total board positions. A board position or setup is technically the picture of the chessboard just after a ply including the initial one.

• B.    Evaluation Score

The games are then batch annotated from 1 to 10,000 out of the 1,27,811 in the database. The annotations by Stockfish appended the evaluation scores of a move just after the half-move notation in the format 1. e4 {[%eval 0.00]} 1. … e5 to make it easy to process the score afterwards. The engine was constantly run on depth 17 i.e. engine annotated the calculated score not going beyond 17 half-moves in the tree to search and calculate the board evaluations. Board evaluations or evaluation scores indicates the situational advantage at a particular instance in respect of white’s perspective in numerical format. A positive number indicates that the white is comparatively in a better position while a negative number means the black side looks in better position. The number is numerically related to the material evaluation of different chess pieces as 1 for pawn, 3 for a knight or bishop, 5 for a rook and 9 for a queen. Besides the material advantage, the score also includes the factor of positional and tactical advantage. For example, an evaluation of +1.8 roughly means white has an advantage of equivalent of 1.8 pawns worth of material than black. The database is then exported as whole to a 121 MB PGN file.

• C.    Text-processing

  The PGN file is then converted to a text format before removing invalid UTF-8 characters. Using bash programming and Notepad++, it is then text-processed to make it more program-friendly, for example, by adding carriage return following a line feed to the end of each line, making each line containing no more than one halfmove, appending evaluation score in the same line as of the move and removing invalid blank lines finally. The games after the 10,000th one are then deleted to generate a 26 MB text file which is our final source for generating the data points for machine learning algorithms. Using Python with the ‘xlsxwriter’ library, data points namely move number, move tree, current move, evaluation score, opening classification, player ratings and the game result is fetched to an excel sheet. Here and in chess, openings are the sequence of initial moves and those which are considered standard are classified in the Encyclopedia of Chess Openings (ELO) [33,34,35]. As the moves were taken from hundreds of thousands of games between masters since 1966, opening moves among them are still employed by most of the players and almost every game played now initiates with an opening already defined. Players choose to play among these since theories and deep analysis over these openings gives them an insight of tactical or positional advantage. Our idea is to make our algorithm learn from the outcomes and board evaluation of these initial moves and then suggest a single or sequence of moves for new chess games. Since we are interested in finding the relationships between the set of initial moves in the database, we have generated different datasets according to pre-defined number of half-moves, i.e. 10, 15, 20. Most of the openings half-moves range from 10 to 20 and on an average, the number of moves with exactly the same move tree decreases beyond 15

half-moves from where the move search tree shrinks to a constant or very less move frequencies which having no considerable variation would not be suitable for our learning algorithms. Although we have used Excel formulas and VBA scripting for calculating more of the derivable attributes mentioned further, Tcl could also be used to interact with SCID vs. PC by following the programmer’ reference provided on [36]. We produced various dataset related to each combination of classification, further described in results.

• D.    Machine Learning

The generated Comma Separated Values (CSV) files from Excel are then fed to machine learning algorithms accordingly. Some of the fundamental attributes existing in anyone of the datasets are briefly described as:

• •    Move number: The number denotes the current sequence number of the played move by one side. When we say that we are using a 20-move dataset or that the engine is running on depth 20, we mean about the total number of half-moves or ply whereas the attribute in the dataset denotes the move sequence corresponding to a side. Note that the PGN format also doesn’t mention half-moves. Move classification is also used in another column that appends letter ‘a’ for white’s ply and ‘b’ for black’s ply to the numerical move number.

• •    Move details: It denotes the move details with the move number in algebraic notation. The move detail can be only about the current move or can contain previous move sequences too. For the former one, we implement the Markov Decision process [37] i.e. the algorithm only considers about the current move and not the past ones. Although, this is a very general approach and can be a conflicting attribute for some cases, it is still the most optimal one. The latter one considers all of the previous moves that made it to the current move which grows sequentially with the move numbers since all of the previous moves are appended before the current move. This approach finds exact move sequences and is a more specific case for the evaluations but requires more space and time for computations.

• •    ECO: Chess Opening classification by Encyclopedia of Chess. The classification is based on the moves played that correspond to one of the openings defined in the ECO.

• •    ELO: FIDE Elo rating of the player on one side according to the move classification.

• •    Result: The game outcome – 0 for black win, 1 for white win and 0.5 for draw.

• •    Evaluation score: Pre-computed move evaluation score by Stockfish engine running on depth 17.

• •    Winning score: The winning score is calculated by calculating the weighted sum of the number of games won and/or draw by playing a move divided by the total number of moves in consideration. The total number of moves can be either accounted from

the whole database of ScidBase or only the considered subset.

There are also derived attributes in the Excel sheet that are calculated from the basic ones. They are mentioned as per usage in Section IV. These datasets are accordingly used in the techniques as per the implementation. The implementation for each of the technique is briefly described as follows:

• •    Multi-variate Linear Regression: For this technique, mainly two classes of datasets are used. First one is the additionally generated 1002-move dataset extracted from the first 183 games in ScidBase for experimental basis. The move details in this dataset doesn’t contain the previous move sequence but only the current move, hence, implements Markov decision process. Also, the winning score is extracted from the ‘Tree Search’ of SCID which is calculated with respect to the total number of games in the database i.e. 1,27,811. The second class consists of three datasets of 10,000 games generated by code with move sequences restricted to 10, 15 and 20 half-moves in each game. The different sets of attributes are compared with respect to their p-values and indicated significance. A comparison for features like standard error and confidence value between the result all of these datasets is also generated.

• •    Na ve Bayes Classification: Different combinations of attributes are analyzed and the comparisons between all of the sets are made. The validation is done on 20% of the datasets in each of the three datasets mentioned above. Accuracies for each combination are compared. The same set of three datasets is used here as well but new discrete attributes are derived from the initial ones to make classifications possible. The derived attributes are described in Section IV in relation with the implementation.

• IV.    Results

This section describes and interprets the result generated through the implemented techniques. Results are sub-divided corresponding to the different machine learning techniques used.

• A.    Multi-variate Linear Regression

  Considering the basic set of 1002 moves, a relationship between the game outcome and the numerical variables like move number, evaluation score and winning score is developed. This model, as mentioned before, follows Markov Decision process and only considers the current state of the game. Considering winning score ( win_score ) and evaluation score ( eval ) only as predictor variables, p-value for winning score comes to be around zero (2e-16) on 997 degrees of freedom. The residuals depict the error between actual and predicted values in Fig. 1. The equation of the generated relation is

  result = 1.017448 * win _ score + 0.004601* eval + 0.012608

with R² = 0.2349 .

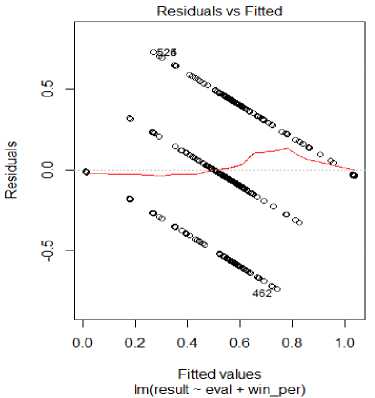
Fig.1. Residuals vs Fitted (with no move number)

This denotes that past data for outcomes of games with similar subset of move sequences do have a strong statistical relationship with current game result, at least, in the ScidBase dataset. Also, the prediction for draw is very much accurate for this dataset while the prediction values for white win has a large standard error than the black win. On using the same dataset on single predictor value of winning score, the graph comes out to be similar as Fig. 1 and there’s only a difference of 0.0002 in R2. When move number (move_no) is added as a predictor variable, the p-value for this variable comes out to be 0.00995 which indicates that the relationship is fairly dependent on the move sequences too. Again, the residual error is least for draws. The equation is now given by result = 0.999787 * win _ score

- 0.011369* eval                       (2)

+ 0.007488* move no - 0.006512

with R² = 0.2349 which indicates the slope coefficient of evaluation score is negative which should not be the case as for a positive change in result, evaluation score should increase with respect to white side. This could mean that in spite of deep evaluation scoring by computers, the game outcomes have a considerable probability for favoring the opposite side too. On removing the eval variable from this now increases the p-value of move_no variable to 0.0129 and R² is again only reduced by 0.0005 to 0.2282. We get the p-value for eval when it is the only predictor variable as 0.662 which is very large in order to reject the null hypothesis. On adding move_no with eval now, we get R² = 0.005185 and the residual graph as depicted in Fig. 2.

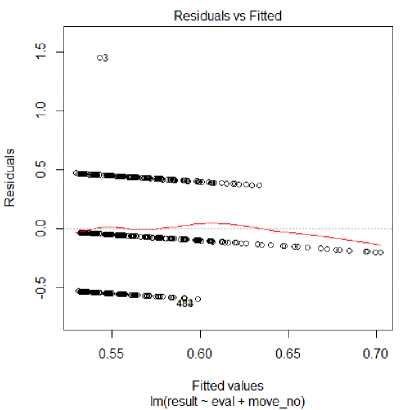
Fig.2. Residuals vs Fitted (with eval and move_no )

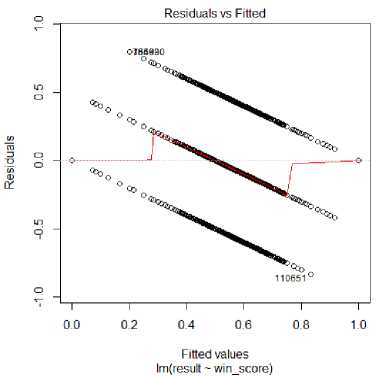
Fig.3. Residuals vs Fitted (20-moves)

The second class of dataset consists of complete move sequences and winning score is now calculated with respect to the dataset only. The formula for calculating winning score, win_score , for a move is the weighted sum of number of games with white win, n white , and with draw, n draw , on playing the exact move sequence divided by the total number of games with the same move sequence and is given by (3) as:

win

1* n white + 0.5* n draw score = ---------------

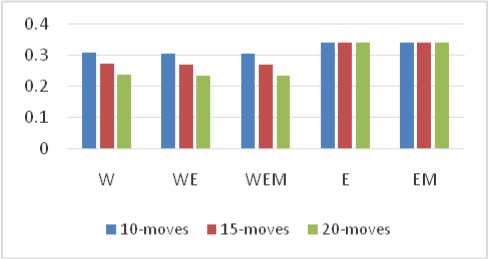
Fig.4. Residual Standard Error

n white + n draw + n black

On using winning score as the single predictor variable in 10-moves dataset it was observed that the residuals are minimum for fitted values between 0 to 0.2 (black win) and 0.8 to 1.0 (white win). Also, the prediction values corresponding to draw (0.5) are again good. The graph is no different from this when another predictor variable, eval , is added. Same is the case with further adding move_no with also no change in residual standard error and R-squared. With eval as the only predictor variable, R2 = 0.001261. Here again adding move_no gives no change. On processing regression on 15-moves and 20-moves data-set, the residuals were seen getting closer to zero in either side of the game result (black and white win) with increasing in the limit of considered moves while a more linear relation is being developed in the draw region as depicted in Fig. 3 for 20-moves.

The variable change in residual standard error and R-squared is similar to the 10-move case. A comparison between these values is also depicted in Fig. 4 and Fig. 5 where W,WE, WEM, E, EM denotes the combination of predictor variables used as W for winning score, E for evaluation score, M for move number. The 20-moves dataset consisted of 2,16,315 number of rows i.e. the algorithm learnt through these number of board positions. Beyond these number of moves, the dataset would have moves with very low number of similar moves, hence, less variation.

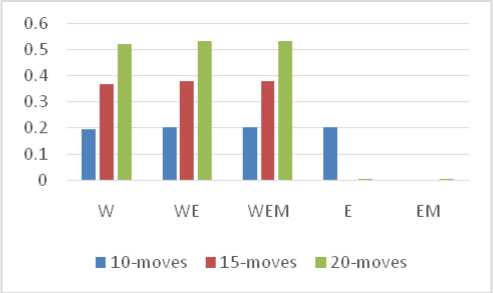
Fig.5. R-squared

• B.    Naïve Bayes Classification

The classification using different combinations of attributes is tested for their accuracies. The validation is done on 20% of the dataset. Some new attributes are defined and derived from the existing ones for this classification. Since techniques based on classification uses discrete data elements, attributes like evaluations and winning score are modified accordingly. The derived variables namely eval_bin and win_bin can now be classified into three classes numerically similar to the result. The value for the variable eval_bin is derived using eval and is calculated as follows:

0, eval < 0 eval bin = ^^^^^^~ 0.5, eval = 0 (4) .1, eval > 0 while variable win_bin is calculated using win_score as:

	'0,	win_score <  0.5
win bin = ■ _	0.5,	win_score = 0.5         (5)
	. 1,	win_score > 0.5

The accuracies of result prediction for the validation set are compared for different combinations of attributes and different datasets. Some of them are depicted in Fig. 6. Here W refers to win_bin , E to eval_bin , D to move sequence and C to ECO classification while M refers to the same as move_no . The accuracies for 20-moves dataset are higher for all combinations but the combinations of (win_bin, eval, ECO, move_no) and (eval, move_no) . The latter one produced the same accuracy for each dataset. Removing or adding eval didn’t affect the accuracies in most cases. 20-moves dataset produced most of the accuracies above 60% while all the datasets were able to produce more than 50% accuracy in almost every combination. The highest accuracy of 66.91 is achieved when ECO and win_score are used for classification. Just like the regression technique, this also indicates the significance of past data in prediction.

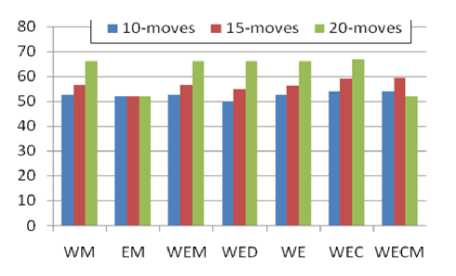
Fig.6. Accuracies of classification

• V.    Conclusion

The results indicated a high significance of winning scores in predicting the outcomes of games. Other attributes like move number and opening classification performed fairly as well. By using move number and move sequences in classification, they remove the ambiguity of considering different game trees that lead to same current move. Variable associated with ECO can be used to classify different openings one of which could possibly be followed. The dataset was observed to provide better classification accuracies when increasing the limit on number of half-moves considered in each game. We have used only a small fraction of total available game database and we assume that accuracies can be further improved with using larger database for the described techniques. More precise classifications can also be developed with larger datasets and more number of different attributes. Chess engines of the current generation also consider opening and theory books for faster board evaluation. However, on devices with low computational power and memory, the proposed regression techniques can take decisions immediately once learning is done since post learning, it only needs to predict the outcome using numerical scores which are very efficiently solved even by common computers. Cloud computing can also be used to learn and classify data and to predict results or suggest moves afterwards. As mentioned in the introduction section, following the winning score approach in the versus-computer game, white won 20% of the games drawing the rest while black tied in 20% of another game set losing the rest. Once the frequency threshold (the minimum number of past games that have to be in record for following the approach, here 10) is reached, the game was finished by same engine strength on both sides and the outcome was noted. Due to first move advantage [23] for white in chess, white has a winning score of 54.95% as calculated from a huge database mentioned in [24]. Considering this theory, the winning scores as a significant parameter for determining outcome performed well on black side too. This way the decision for the next move is taken immediately at least for the initial moves. A significant amount of time on the side of implementation is also reduced and the residual time can be used in mid-games or end-games in timebound matches. In faster versions of gameplays like Bullet Chess which lasts for few minutes only, optimal move prediction in less time is required more than determining the best move which takes considerable amount of time. Winning score can determine the optimal move immediately while saving the remaining for later complex board positions. Since the implemented algorithm in this paper is much generalized with respect to chess trees and gameplay, we would be working on complex implementations on similar approach proposed here.