Statistical Hiding Fuzzy Commitment Scheme for Securing Biometric Templates

Published Online April 2013 in MECS

In cryptography, commitment schemes are commonly two-phased; (commit and open) cryptographic protocol, ensures secure communication between two parties, with complete disillusionment of information for mistrusted parties. The sender, A, and the receiver, B. At the end of the commit phase, the sender, A, is committed to a specific value, in which the scheme satisfies the following constraints: (1) The receiver, B, learns nothing about a committed value before the open phase (this is known as the hiding property), (2) The sender, A, is bound to at most one value (this is known as the binding property). In the open phase, the sender, A, sends extra information to the receiver, B, which allows him to determine the committed value. Commitment schemes are conventionally opened using identical information. However, there are several security applications noisy inputs could not be avoided such as biometric systems. Therefore, it is important to protect the biometrics information whenever replaced password/key in authentication systems. A solution to facilitate the use of approximate information in cryptographic systems is achieved by combining techniques from the areas of cryptography and error correcting codes.

In 1997, Crépeau [1] introduced a bit-commitment scheme based on error correcting codes. The scheme is apply a binary symmetric channel (BSC) to a binary codeword from the set of error correcting codes. In [2,3], a cryptographic primitive is proposed to enhance the biometric template protection. The scheme is a synthesis of techniques from the areas of error correcting codes and cryptography. The drawbacks of the scheme are leads to leakage of information about the user’s biometric data [4] and the error tolerance of the scheme is small (the authors assumption that only up to 10% bit of the iris code can be corrected). In fact up to 30% bits of the iris code could be difference between different presentations of the same iris [5].

In [6], Juels and Wattenberg proposed theoretical basis for biometrics protection schemes that they referred to as “fuzzy commitment scheme” (FCS). The Juels and Wattenberg’s scheme can be seen as a generalized and improved of [2]. In the last decade, the FCS became a popular technique for designing biometrics secrecy systems [7]. However, the fuzzy commitment scheme (FCS) is solely based on cryptographic hash function SHA1. By considering the security flaws in cryptographic hash functions such as MD5 and SHA1 families, and any commitment scheme designed through hash function has been proved to be false solution [16]. Furthermore, Commitment schemes based on noisy channels has been discussed briefly in [35, 36]

In [8], Juels and Sudan derived a fuzzy vault scheme from the fuzzy commitment scheme which is based on the hardness of polynomial reconstruction. Several concepts of cryptographic primitives based on error correcting codes have been introduced, referred to as “fuzzy extractors” and “fuzzy sketches” [9-15].

Motivated by above examples that shows the importance of securing biometrics systems, and the question how to improve Juels and Wattenberg’s scheme in a secure way, this paper proposes general fuzzy commitment scheme called an ordinary fuzzy commitment scheme (OFCS), in which the security of the Juels and Wattenberg’s scheme is resolved and many fuzzy commitment schemes with variety complexity assumptions constructed. Our scheme is provably secure against all power computation adversary receiver and computation bounded adversary sender. The efficiency of our scheme offers different security assurance, then the systems usage become non-trivial. Mathematical analysis and proves are provided in detail to show that our scheme is secure and efficient.

Moreover, we exploit our OFCS scheme to enhance the security of biometric authentication systems. If the biometrics template is compromised, then there is no way to use it directly again even in secure biometrics systems. This paper combines biometrics and OFCS to achieve biometric protection scheme using smart cards with renewability of protected biometric templates property.

The rest of the paper is organized as follows: In section 2 we give background theory in error correcting codes and biometrics. Section 3 reviews Juels and Wattenberg fuzzy commitment scheme and describe its security flaw. The proposed ordinary fuzzy commitment scheme and corresponding security analysis is presented in Section 4 and 5, respectively. In Section 6, we present several constructions of ordinary fuzzy commitment scheme . In section 7 we discuss an application to biometric identification systems. Finally, we draw our conclusions in Section 8.

• II.    background theory

• A.    Error correcting codes

Error correcting codes are used for detecting and correcting errors when data transmitted from one place to another over a noisy channel. They naturally find applications where fuzziness’ may creep in [2,3,6,8], especially because like noise fuzziness is a noise like effect which needs to be carefully accounted for. Following definitions and terminology would be fundamental to our discussions.

Definition 1 (code set C): Let C be a proper subset of { 0,1 } n , with 2 k elements. Then we refer to elements of C as codewords of length n and, 2 ^k the size of the code. We denote the code set as C ( n , k ) .

Definition 2 (Hamming distance): Given a code set C ( n , k ) as defined above, The Hamming distance between any two codewords c and c of the code set C is given by:

1 ⁿ

H dist ⁽ c i , c j ) = -Z I c i - c j I ⁽¹⁾ n г = 1

Definition 3: Let M = {0,1} ^k be a message space. The function g : M ^ C which we call an error correction encoded function, represents a one-to-one mapping of messages to codewords. (conversely, g ^{- 1} is the inverse of g which used to retrieve the transmitted message from the reconstructed codeword).

Definition 4: The maximum number of errors that can be corrected in the corrupted codeword is called error correction threshold of the error correcting code C , and denoted by t .

Definition 5: (Error correction decoded function): An error correction decoded function f : { 0,1 } n ^ C U 1 , for a code set c is defined as: For any c ' e {0,1} ⁿ ,

[ c     If H. Tc ', c) < t, f (c) = {              dlstV , 7 sh                               (2)

• [1 otherwise

where 1 is denoted that an invalid codeword.

Definition 6 (Statistical distance): Let X and Y be two random variables over the same sample space, and let D and D be their associated discrete probability distributions. Then, we defined and denoted the statistical distance between D 1 and D 2 as follows:

S dist ( D_v; D 2 ) = £| Prob[X = a ] - Prob[Y = a ]|      (3)

ae^

• B.    Biometrics

A biometric system is defined as the automated measurements of physiological or behavioral characteristics (e.g. fingerprints, facial geometry, iris patterns, retinal patterns, hand geometry, voice prints, or, DNA) to determine, verify, or identify of a human being [17,18] . A Biometric authentication system performs automated authentication of users depending on their physical and behavioral characteristics. Such an authentication system consists of several basic modules:

Biometric Sensor Module: The biometric sensor requires users to present their biometrics in the form of an image and therefore the analog to digital conversion. The output of the biometric sensor is the raw biometric data. The sensor is used at the enrollment of a user and every time a user needs to be authenticated.

Feature Extraction Module: The raw data are processed and analyzed. The result of the feature extraction (template) should be the most distinctive features for every user. Feature extraction is performed during the enrollment process as well as during an authentication.

Matching Module: The biometric matching module is requires that the user present their biometric for reading, template generating process is also applied here, and compared with the stored template. Then match score is generated. Matching is performed whenever a user needs to be authenticated.

Decision Module: The process of determining or authenticate the identity of the user.

The two basic processes of a biometric authentication system are the “enrollment" process and the “authentication" process. In the enrollment process of a biometric authentication system, all users are registered with the system, and biometric references data x is stored in the database of the system. On the other hand, the authentication process denotes the process of identity verification or determination. In this process the authentication system performs a comparison between the presented biometrics x and the stored references of the previous enrollment phase according to some metric distance.

• III.     Related work

• A.    Review of Juels and Wattenberg’s scheme

  In 1999, Juels and Wattenberg combined well known techniques from the areas of error correcting codes and cryptography to achieve a new type of cryptographic primitives referred to as fuzzy commitment scheme (FCS).

The fuzzy commitment scheme consists of a function F , used to commit to a codeword c e C ( n, k ) and a witness x e {0,1} ” , where both c and X are n -bits string. The difference vector 5 e {0,1} ” , where 5 = x — c , and the hash value h ( c ) are stored as commitment F ( c , x ) = ( h ( c ), 5 )  . To open  the   commitment

F ( c , x ) = ( h ( c ), 5 ) using witness X ' , the receiver computes the codeword     f ( c ')   and verifies

?

h ( f ( c ')) = h ( c ) . If it holds, the commitment F ( c , x ) = ( h ( c ), 5 ) has been successful opened. Otherwise x ' is an incorrect witness.

The idea of “ fuzziness of x ” that each x ' is sufficient “close” to the original x , according to an appropriate distance metric, such as Hamming distance, but not necessary identical. The difference vector 5 used to translate x ' in the direction of x , facilitating to reconstruct the codeword f ( c ') [6].

• B.    Security flaw of Juels and Wattenberg’s scheme

  The Juels and Wattenberg scheme is a simple commitment construction based solely on cryptographic hash function “the sender commit to a secret message c h ( c )”. Obviously, the amount of information about the codeword and the witness is hidden in the hash value h ( c ). However, such strategy is not secure enough [16], because the cryptographic hash functions such as MD5 and SHA families are proven theoretically and practically vulnerable to collision and second preimage attacks (RFC 4270). Furthermore, several researchers have noticed serious security flaws and vulnerabilities in most widely used MD and SHA families [19-27]. Moreover, in

  response to a SHA-1 vulnerability announced in Feb. 2005, NIST (National Institute of Standard and Technology) was apparently not confident in the strength of SHA-1 [28].

Therefore, the Juels and Wattenberg’s scheme not satisfy the hiding and binding properties of commitment schemes and hence the systems using it are not secure.

• IV.    The Proposed Ordinary Fuzzy Commitment

Scheme

An ordinary Fuzzy Commitment Scheme is three-phase (Setup, Commit and Open phases) represents by the tuple { M, X, Y, K, ECCS, FPCK_f, P, E ( e,, t, ) } where:

M : A set of all possible resources (message space) states, not necessarily binary?

X : A set of witnesses states.

Y : A set of all possible fuzzy commitments.

K : A set of indices k encoded by unary (1 ^k ), which we call it the security parameter.

ECCS : Error Correcting code System { C , g , f } , where C ( n , k ) is a code set, g is a error correction encoded function and f is an error correction decoded function.

FPCK : A family of fuzzy public commitment keys (fuzzy PCK). For each k e K , there fuzzy PCK, F:g(M) x X ^ Y , which is denoted and defined as:

F( g (m), x) = (e, 5), where 5 = x—c , is called the difference vector and the e = Fk (c, x) is a conventional commitment scheme computed using the public commitment key F : CxX ^E.

P : A set of individuals, generally with three elements A as a committing party, B as the party to which a commitment made and Ted as the trusted party.

E ( e , t_t ) : A set of events occurring at times t and carried out by the algorithms e for i = 1,2,3.

The scheme is illustrated in Fig. 1. Initially, the environment is setup according to Algorithm 1 labeled by Setup (event e ) occurs at time t .The Ted selects security parameter k e K and generates the parameters of the fuzzy PCK, F .

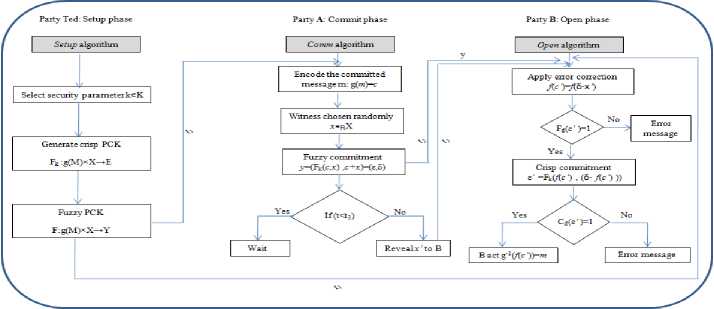
Figure 1: The proposed ordinary fuzzy commitment scheme

Algorithm 1: Setup phase of the OFCS scheme. This procedure is run by the trusted third party Ted.

Input: Security parameter k encoded by unary 1 ^k .

Setup (1 k ) ^ param ( F )

Output: A parameters of the fuzzy public commitment key - param ( F ) .

Then the fuzzy PCK F: g (M) x X ^ Y of OFCS scheme defines as F( g ( m ), x ) = ( F_k ( c, x ), x — c ) = ( e , 5 )

The trusted third party Ted publishes the fuzzy public commitment key F: g (M) x X ^ Y to both the sender A and the receiver B (after that the Ted becomes inactive).

During the commit phase, the sender commit to his secret message m e M using Algorithm 2 labeled by c omm (event e ) occurs at time t .

Algorithm 2: Commit phase of the OFCS scheme. This procedure is run by the sender A .

Input: A secret message m e M and the fuzzy public commitment key F .

• •    Compute c = g ( m ).

• •    Choose a random witness x e„ X .

R

• •    Compute the commitment E = F k ( m , x ) .

• •    Compute the difference vector 5 = x — c .

Output: A fuzzy commitment y = ( e , 5 ) .

The sender A sends the fuzzy commitment y to the receiver B at time t₂ . When the time reaches t >  t₂ ( ( 1 3 ) ), the sender reveals the opening key op_ke = x ' to the receiver. Then the receiver make use of the opening key to execute the open phase according to Algorithm 3 labeled by Open (event e ) occurs at time t .

Algorithm 3: Open phase of the OFCS scheme. This procedure is run by the sender B .

Input: A commitment y , fuzzy public commitment key F and the opening key op_te = x '.

• •    Compute f ( c ') = f ( x ' — 5 ) .

• •    Fuzzy decision making; verify F_d( f ( c ')) = 1. If true,

• •    Compute     the     crisp     commitment

e ' = F_k ( f ( c '),( 5 — f ( c '))).

• •    Crisp decision making; verify C_d ( e ') = 1 . If true, Output:  The committed message is accepted as

m = m ' = g *( f ( c ')) . Otherwise an error message, invalid opening key is revealed.

• V.    security analysis

In the design of any commitment scheme, hiding and binding properties are the most important security aspects to be considered. In this Section we investigate the security of the proposed ordinary fuzzy commitment scheme with respect to all power computation receiver (hiding property) and computationally bounded sender (binding property). To simplify our analysis, It should be noted that the definitions of message space is M = { 0,1 } k , the witness set X = { 0,1 } n and code set C c { 0,1 } n . These sets are independent random variables over the same sample space { 0,1 } n . Furthermore, these sets are finite and all their associated probabilities distributions are discrete. Also we will assume that the operation “+” is exclusive OR and denoted by “ ® ”.

• A.    Hiding Property

The hiding property characterizes the resistance of the scheme against attempts carried out by an adversary receiver B * to determine the codeword c or the witness x , from the fuzzy commitment y = ( e , 5 ) . We assume that the adversary receiver B * knows F k and has an access to the fuzzy commitment pair y = ( e , 5 ) . Then an adversary may be compromises the committed codeword from either the difference vector 5 or the conventional commitment E = F_k ( c , x ) .

Lemma 1: Suppose that X and Y are two independent random variables over the same sample space ψ . Let Z be a random variable obtained by exclusive “OR” of X and Y. Then, the three random variables X, Y, and Z are pair-wise independent.

Proof : Let X and Y are two independent random variables over the same sample space ψ . So we have, Prob[X = u,Y = v] = Prob[X u]Prob[Y

<------

|X||Y|

Now, let Z = w , such that w = u © v , and thus v = w © u. Since the variables X = u and Y = w © u are independent random variables, therefore X and Z. Similarly, Y and Z are independent.

Theorem 1: Suppose that X (witness space) and C (error correcting code set) are two independent random variables over the same sample space {0,1}n , and let

Z = { 5 = x © c : x g X, c g C } be a random variable obtained by “exclusive OR” of elements of X and C . Then, the probability that an adversary receiver B * is able to compute either c or x from the difference vector is no more than 2^{- k} , where k is the size of the error correcting code C .

Proof: Assume that X and C be two independent random variables over the same sample space {0,1}ⁿ , clearly |C | = 2 ^k and k <  n , thus

Prob[X = x ,C = c ] = Prob[X = x ]Prob[C = c ] < Tq¹ (5)

Let Z = { 5 = c © x : c g C, c g X} be an event obtained by “exclusive OR” elements of X and C . Thus Z, X , and C are pair-wise independent random variables (Lemma1). Hence we have

Prob[X = x | Z = 5 ] = Prob[X = x ] <  T ,           (6)

and

Prob[C = c | Z = 5 ] = Prob[C = c ] <  T              (7)

Therefore

Prob[X = x |Z = 5 or C = c | Z = 5 ] =Max{Prob[X = x ], Prob[C = c ]} <  2 - ^k (Max: means minimum of two numbers).

Definition 7: [Statistically hiding measure]

The OFCS scheme is X -hiding if for any two codewords, c = g ( m ) and c₂ = g ( m ) , such that ^H dist ^{( c} 1^{, c} 2⁾ >  t_sh are secured using the same F_k . The distributions D ( c ) and D ( c ) given by:

D ( c ) = Prob[ F ( c , x ) = 8 , for some x g X]

= £ Prob[ x ]HProb[ 8 | x ]                             ⁽⁸⁾

xgX and

D ( c ₂) = Prob[ F ( c ₂, x ) = 8 , for some x g X]

= £ Prob[x]HProb[8 | x]                              , xgX

(9) are two probability distribution over the same sample space.

Then,

S ds ( D( q X D( c 2 )) = X                           (10)

Eq (10) states that an adversary able to distinguish between what sender committed to, only to extend of measurable difference given by X . To provide a measure of the hiding property, X = 0 -hiding represents the perfect OFCS hiding and the weakest OFCS hiding is given by X = 1 -hiding. In the following theorem bound derivation for statistically-hiding property.

Theorem 2 [Hiding-Measurement] For any k g K , let F: C x X >  Ybe a fuzzy public commitment key. Then, an ordinary fuzzy commitment scheme based on F is X -hiding and the value of X is always computed as: For c = g ( m ) and c₂ = g ( m )in C

S_dlst ( D (q), D ( c 2 )) = 2 ^{- 2} n £ | p_E c - p , . c ₂ | = X         (11)

8GE

Proof :

For given c = g ( m ) g C , let D ( c ) be a probability distribution on the code set C , defined as D ( c ) = Prob[ C = c : F ( c , x ) = 8 ].

For any 8 g E, let p_gc be the size of pre-image set

Q ₈ ( c ) = { x : F_k ( c , x ) = 8 } .

For fixing 8 g E , D ( c ₀) is defined by:

D ( c _k) = Prob[ C = c ₀ : F ( c ₀, x ) = 8 ₀, for some x g X] = £ Prob[ x ]DProb[ F ( c ₀, x ) = 8 | x ]

x g X

Then for some value x₀ g X,

^Pro b[ ^F k ( c o , x o ) = ⁸ 0 1 x o ] = Prob x o : F k ⁽ c o , x o ) = ⁸ 0^]

2^{- n if} x o ^g^ 8 ( c o )

0 Otherwise

Hence

D ( c ₀) = Prob[ F ( c ₀, x ) = 8 ₀, for some x g X]

= £ Pro^b[ x I Probl F k ⁽ c o , x ) = ⁸ o | x ^]          (14)

x g X

2 - n   X ¹    -- n    /^-2 n _

£  2  = 2  P8o, co xg^80 (co )

Assume that the receiver can find two codewords c and c₂ in C , such that H_dist ( c_x , c ₂) >  t_sh and F ( c , x ₁) = F ( c ₂, x ₂) = 8 for some x_x , x₂ g X . Thus,

S dist ( D ( c 1 ), D ( c 2 )) = ∑ |Prob[ F k ( c 1 , x ) = ε ] - Prob[ F k ( c 2 , x ) = ε ]|

= ∑ | ∑ Prob[ x ]Prob[ F ( c , x ) = ε ] - ∑ Prob[ x ]Prob[ F ( c , x ) = ε ]|

ε ∈ E x ∈ X                                      x ∈ X

≤ ∑ |2 ^{-2 n} ∑ 1 - ∑ 1|

ε ∈ E         x ∈Ω _ε ( c ₁)      x ∈Ω _ε ( c ₂)

= 2 ^{-2 n} ∑ | ρ ε , c ₁ - ρ ε , c ₂ | = λ ε ∈ E

• B.    Binding Property

The binding property of our OFCS scheme characterizes the resistance against attempts carried out by an adversary receiver A * to determine the codeword c ' such that H_dist ( c , c ') > t_sh and F_k ( c , x ) = F_k ( c ', x ') = ε , for some x ' ∈ X.

Definition 8 [Computationally-binding measure] The OFCS scheme is η -binding if for any distinct codeword c ' ≠ c ∈ C such that H ( c , c ') >  t      and

F ( c , x ) = F ( c ', x ') = ε , for some x , x ' ∈ X , with knowledge of public commitment key F and the fuzzy commitment ε . Then:

p rob [ c ', H_dist ( c ', c ) > t_sh : F_k ( c ', x ') = ε , x ' ∈ X] ≤ 2 ^{-2 n} ρ_{ε , c '} = η      (15)

Theorem 3 [Binding -Measurement] Let F : C × X → Y be the fuzzy PCK. Then, an ordinary fuzzy commitment scheme based on the fuzzy PCK is η –binding and the value of η is always be computed as follows:

Prob[ c ', H_dist ( c ', c ) > t_sh : F_k ( c ', x ') = ε , x ' ∈ X] ≤ 2 ^{- 2 n} ρ_{ε , c '} = η

Proof :

Assume that c = g ( m ) ∈ C , x ∈ X , and F ( c , x ) = ε be the commitment in the fuzzy commitment y . Let ρ be the size of pre-image set Ω ( c ) = { x : F ( c , x ) = ε } .

Our task is to find the probability that an adversary sender A* finds an opening key x ' ∈ X, with H_dist ( x , x ') = H_dist ( c , c ') > t_sh such that the equality F ( c , x ) = F ( c ', x ') = ε , holds.

Fix a codeword c ' ∈ C and Using Eq.(13) and (14)

Prob[ c ' : F ( c ', x ') = F ( c , x ) = ε , x ' ∈ X]

= ∑ Prob[ x '] Prob[ F ( c ', x ') = ε | x '] x ' ∈ X

≤ 2 ^{- 2 n} ρ ε , c ' = η

• VI.    Constructions of ordinary fuzzy commitment

SCHEMES

This section introduces several constructions of an ordinary fuzzy commitment schemes. We distinguish between number-theoretic constructions [29,  32-34]

applying the hardness of factoring for instance, existence of collision-free hash functions –based constructions and complexity-based construction using general cryptographic assumptions like the existence of Pseudorandom generator.

• A.    Factoring –Based Construction

The factoring-based ordinary fuzzy commitment scheme is based on Halevi’s conventional commitment [29]. To set up the factoring–based OFCS scheme the trusted third party Ted runs a Setup (1 ^k ) which will generate a composite number n = p q as a parameter of the fuzzy public commitment key, where p and q are two prime numbers chosen randomly, such that p = 3 (mod8) and q = 7 (mod8) . Halevi used the Goldwasser-Micali-Rivest (GMR) claw-free permutation pairs [18], P , and then the parameter n is given to both the sender and the receiver

To commit to the message m ∈ M the sender chooses a random witness x ∈ X , computes the crisp commitment ε = F ( c , x ) = P ( x ² ) (mod n ) and the difference vector δ = x - c , where c = g ( m ) is the encoded message, then the crisp commitment and the difference vector together sends to the receiver as fuzzy commitment termed F( m , x ) = ( ε , δ ) .

During the open phase, the sender sends the receiver the opening key opkey = x' in which sufficient “close” to the original op = x , according to appropriate distance metric,, but not necessary identical, should be able      to      reconstruct      the      codeword f (c') = f (x'-δ) = f ((x'- x) -c) from the difference vector δ and translate x' into the direction of x , x''=δ-f (c'). After that the receiver computes the crisp commitment ε' = F ( f (c'), x'') and matches ?

against the stored crisp commitment ε , ε ' = ε . If it fails, the receiver does not accept op_key = x ' as an opening key. Otherwise the receiver accept and retrieve the secret message m = m ' = g ^{- 1} ( f ( c ') ) ..

• B.    Collision-Free Hash Function –Based Construction with universal Hash

The collision-free hash function-based ordinary fuzzy commitment scheme is based on Halevi and Micali’s conventional commitment [16]. To set up the collision-free hash function –based OFCS scheme the trusted third party Ted runs a Setup (1 ^k ) which will generate a collision-free hash function h : {0,1}^* → {0,1} ^k , and then the collision-free hash function will given to both the sender and the receiver.

To commit to the message m g M= { 0,1 } k the sender chooses a random witness x g_r X= { 0,1 } n , computes the conventional commitment s = F_k ( c , x ) = ( h ( c ), u ) , where u :{0,1} ⁿ ^ {0,1} ^k be a universal hash function chosen randomly such that u ( c ) = x ,and the difference vector 5 = x - c , where c = g ( m) is the encoded message, then the commitment and the difference vector together sends to the receiver as fuzzy commitment termed F( m , x ) = ( s , 5 ) .

During the open phase, the sender sends the receiver the opening key op_key = x ' in which sufficient “close” to the original x , according to appropriate distance metric,, but not necessary identical, should be able to reconstruct the codeword f ( c ') = f ( x ' - 5 ) = f ( ( x ' - x ) - c ) from the difference vector 5 and translate x ' into the direction of x ,   x ’’ = 5 - f ( c ') . After that the receiver checks

?

u ( f ( c ') ) = x ”. If it fails, the receiver does not accept the opening key. Otherwise, computes the conventional commitment s ' = F_k ( f ( c '), x ") and matches against the

?

stored conventional commitment s , s ' = s . If it fails, the receiver do not accept op_key = x 'as an opening key. Otherwise, the receiver accept and retrieve the secret message m = m ' = g ^{- 1} ( f ( c ') ) .

• C.    Pseudo-Random Generator –Based Construction

The pseudo random generator-based ordinary fuzzy commitment scheme is based on Naor’s conventional commitment [30]. To set up the pseudo random generator–based OFCS scheme the trusted third party Ted runs a Setup (1 ^k ) which will generate a pseudo random generator G:{0,1} ⁿ ^ {0,1}^{2 n} defined as G ( x ) = B (1) B (2).... B (2 n ) , where B(i ) is i^th bit of G ( x ) and a random vector R = ( r 1 , r ₂, , r _{2 n} ) , Such that H dist (0, R ) = n , where r g {0,1} for 1 <  i <  2 n . Then the parameters ( G , R ) are given to both the sender and the receiver.

To commit to the message m g M= {0,1}k the sender chooses a random witness x gr X= {0,1}n, computes the conventional                            commitment f B (i) if r = 0

s = F ( c , x ) = {            i     and the difference vector

• ^k        [ B ( i ) ® c if r = 1

5 = x - c , where c = g ( m ) is the encoded message, then the conventional commitment and the difference vector together sends to the receiver as fuzzy commitment termed F( m , x ) = ( s , 5 ) .

During the open phase, the sender sends the receiver the opening key opkey = x' in which sufficient “close” to the original x , according to appropriate distance metric, but not necessary identical, should be able to reconstruct the codeword f (c ’) = f (x ’- 5) = f ((x ’- x) - c) from the difference vector 5 and translate x' into the direction of x , x' = 5 - f (c ’). After that the receiver computes the conventional commitment s' = Fk (f (c ’), x") and matches

? against the stored conventional commitment s , s ' = s . If it fails, the receiver does not accept op_key = x 'as an opening key. Otherwise, the receiver accept and retrieve the secret message m = m ' = g ^{- 1} ( f ( c ’) ) .

• VII. Fuzzy Biometrics Authentication with

Renewable Template using smart card

The lacks of secrecy of biometrics (e.g., leaving fingerprint impressions on the surfaces we touch, face and eye images being captured by hidden cameras) are identified as the main problems of biometric systems [31]. Unlike replacing key or password in traditional authentication systems, once the biometric template is compromised, there is no way to use it directly again even in secure biometric authentication. In this section, we propose fuzzy biometric authentication with the renewability of protected biometric templates property to overcome this problem, in which the template is privacy protected and multiple fuzzy commitments of the templates can be derived from the same biometric template for the purpose of template renewability. If the biometric template is compromised, then the user needs to register again using the same biometric template with selection of different codeword.

• A.    Registration phase

When the user U needs to register with the system S , they perform the following steps:

• 1.    U chooses a random codeword c from a code set

• 2.    U presents her/his personal biometric data B on the specific device which will generate a biometric template x , and provides the codeword c , and the identity ID to the system S via secure channel.

• 3.    S computes the fuzzy commitment F ( c , x ) = ( s , 5 ) and the ciphertext E ( c ) of the codeword (for the reregistration purpose).

• 4.    S stores ( s , E ( c ), ID ) in the system database and loads ( s , 5 , ID ) in U ‘s smart card, and then sends it to U via secure channel.

C ( n , k ).

• B.    Authentication phase

Whenever the user U wants to login to the system S , she/he must perform the following steps:

• 1.    U inserts her/his smart card into the card reader and presents her/his personal biometric data B on the

• 2.    The smart card computes the codeword f ( c ') = f ( x ' - 5 ) and x " = 5 + f ( c ') , and then the commitment s ' = F_k ( f ( c '), x ") . The commitment s ' matches against the stored s in the system database i.e. ?

• 3.    If the above mentioned verifications failed, the scheme will be terminated and as a result U will not pass this stage. Otherwise, if the above verification holds, the user is authenticated.

specific device which will generate a biometric template x ' .

s ' = s .

• VIII. Conclusion

In this paper, we developed a general fuzzy commitment scheme called an ordinary fuzzy commitment scheme (OFCS), in which many fuzzy commitment schemes with variety complexity assumptions constructed and the security of Juels and Waterberg fuzzy commitment scheme is resolved. The proposed scheme is proved to be resistance to all power computation adversary receiver and computation bounded adversary sender. The efficiency of our scheme offers different security assurance and the trusted third party involved only in the setup phase.

The characteristic of our scheme makes it more effective and promising to design high secure biometrics protection scheme. This paper also proposed fuzzy biometric authentication scheme based on OFCS scheme with the renewability of protected biometric templates property, in which the template is privacy protected and multiple fuzzy commitments of the templates can be derived from the same biometric template for the purpose of template renewability.

Acknowledgment

We would like to thank King Fahd University of Petroleum and Minerals for providing facilities for this research.