Статистическая динамика энергосберегающего рабочего органа для шелушения зерна

технологическая схема шелушения зерна, предусматривающая установку на одном валу подвижного (нижнего) диска, над которым в общей обойме установлены шесть неподвижных рушащих вставок для шелушения шести фракций гречихи. Под каждую неподвижную вставку подведен зернопровод. Таким образом, на каждом рушащем поставе размещен один подвижный диск, шесть рушащих вставок, шесть зернопроводов и шесть бункерных емкостей с шестью разными фракциями гречихи для получения крупы . Плоскости между поверхностями подвижного диска и рушащими вставками параллельны . Зазоры между и общей поверхностью подвижного диска и плоскостями неподвижных рушащих вставок разные и соответствуют размерам для шелушения шести фракций зерна.

Анализ составных элементов функционирующей системы позволяет установить физико-механические закономерности, сопровождающие рабочий процесс, синтезировать общую технологическую и конструктивную схему миникомплекса и определить его качественные показатели. Кинетика процесса подачи и закономерности распределения зернового потока на круге носят случайный характер и могут быть описаны математическим аппаратом случайных функций и их вероятностно-статистическими моделями. Для построения статистической модели входящего потока зерна будем считать его как неубывающий случайный процесс X(t), принимающий дискретные целочисленные значения. Функция X(t) определяет количество зерен, поступающих на рушащий орган, и сохраняет динамические свойства всего потока на интервале (t + At). В виду большого числа совокупно действующих факторов и сложности детерминированных методов исследования динамики рабочего процесса, при построении модели входящего потока на него накладываются ограничения.

• 1)    Статистические процесс пода чи з е рна, режимные пара м е тры ус тро йс тв а и и х х а ра кте р ис т ик и приняты установив ш и мис я и не из м е н яются в о времени. Этим оп ре дел яе тся ус л овие с та ц иона рнос т и входящего пото к а в си с т е му. Ве роятнос ть поя в л ени я зерна на интервале ( t + At ) не зависит от его расположения н а диске, а определ яе тс я т о л ько интенсивностью пода чи ин те рв а л а , д л я ко торого вероятность равна [1], [2], [3], [4], [5], [6], [7]:

P k ( t,t + At ) = P_k. (1)

Стационарность потока означает е го не и зменность во времени и пространстве.

• 2)    Геометрические соотношения зерна и и х размещение на диске приведены на рисунке 1. Средняя площадь, перекрываемая рабочую ча с ть диска одним зерном, определяется его размерами, которыми являются ширина А , толщина В и длина С . Принятая шири на потока ис к л юча е т попада н ие на интервал t более одного зерна, если t < d_cp. Тогда средневзвешенный размер зерна составл яет :

d _cp = 3/ A • B • C . (2)

Проход для одн ого з е рна чере з ра с х одное сечение на радиусе R ₁ соответствует некоторому среднему углу а, с другой стороны, S = aR 1 .

Если выделим дугу S с углом а обхвата зерна, то мгновенная вероятность (при At ^ 0) попадания двух и более зерен на эту дугу стремится к нулю:

^Р2 ( d cp ) ^ 0, или

Р2 (At )^ 0 •At = 0, где Р2 (At) – вероятность появления двух и более зерен на отрезке дуги S;

0•At - величина второго порядка малости, убывающая быстрее, чем величина угла и соответственно дуга aR 1 .

Таким образом, общий поток зерна разделен на сумму ординарных потоков, проходящих через дугу S окружности радиуса R ₁.

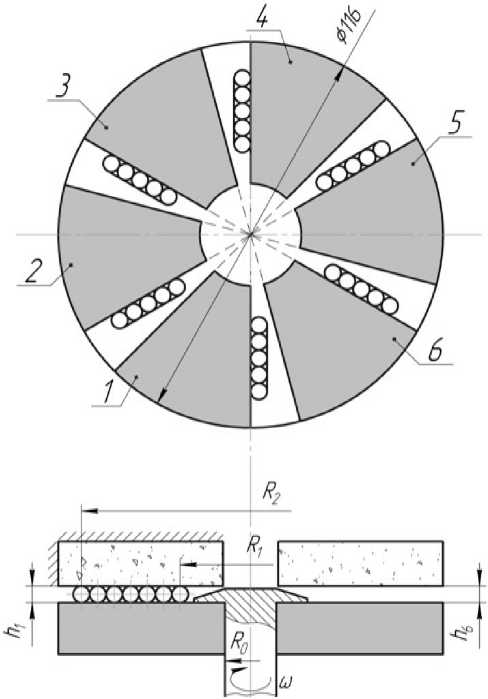
Рисунок 1 – Схема к обоснованию ординарного потока Эрланга динамической модели шелушения зерна

• 3)    Вероятность появления зерна не зависит от того, сколько зерен находится на интервале ( 0 ^t ) , поскольку в ходе рабочего процесса они распределяются случайным образом, хаотично. При этом можно наложить на поток ограничение отсутствия последствия в распределении зерен в пределах площади, ограниченной углом а. Принятая геометрическая модель предполагает такое движение частиц, при котором траектории их центров масс не пересекаются. Принятые и наложенные ограничения и допущения позволяют рассматривать дискретный поток зерна как простейший и применить для его описания хорошо разработанный вероятностный метод исследования, установить закономерности качественных параметров работы системы . Минимальная площадь расходного сечения ординарных потоков равна сумме площадей зерен, находящихся на радиусе подачи R 1 , перпендикулярно к плоскости крута, а высота расходной щели равна среднему размеру зерна d cp , принятого за ширину полосы ординарного потока. Эта площадь равна:

7    2nR,•d

S p = n i • d 2p =       ^{1 cp} = 2nR i • d cp .

d cp

Определим геометрические вероятности использования площади рабочей части круга. При соблюдении условия ординарности на радиусе можно разместить n ₂ зерна:

= R 2 - — d_cp

Тогда общее количество зерен n с учетом пропускной способности площади расходного сечения на радиусе подачи R 1 составит:

2л—, ( —₂ - —, )

n = n i • П 2 =---------- ¹² .         (4)

d c²p

Если средняя площадь миделева сечения зерна принять, равной площади ординарного потока S3 = d2p, то суммарная площадь рабочей части кольца, перекрываемая n зернами, составит:

n

ЕS i = S ₃ • n , или

ESi = dcp • n, откуда

n

ES i = d 2p • n • 0 2 -

Заменяя n1 и n2 их значениями, получим:

n         2 n — ( —9 — — )

E S ₃ = d 2p —¹ •   ----- = 2 n — i ( — 2 — — 1 ) (5)

1              d cp d cp

Если площадь кольца рабочей части круга составляет:

S k — n ( — 2 —— 2 ) ,                 (6)

то геометрическая вероятность использования всей площади круга равна отношению площадей (5) и (6):

P = Fl = dr"-" ;

^{s    S}k     n ( — 2 —— 2 )

Окончательно имеем:

P = -2—^.

^s — 2 + — 1

Уравнения (7) и (8) подтверждают, что принятые допущения и наложенные ограничения не влияют на ход рабочего процесса, который определяется размерными параметрами диска R 1 , R 2 , физикомеханическими параметрами зерна через d_cp .

В этой связи необходимо исследовать вероятностно-статистические характеристики размеров зерна и входящего потока заданной интенсивности, принимая во внимание, что он удовлетворяет условию стационарности, ординарности и отсутствия последействия. Исследуем вероятность (8), полагая, что начальный радиус R1 = 1. Тогда можно записать:

P = -^— s —2 +1

.

Взяв отношение R₂ /R₁ = ( 1, 2, 3, ..., n) и подставив их в уравнение (9), получим экспоненту и числовой ряд (табл. 1) вероятности загрузки диска в зависимости от соотношений R ₂ /R ₁ .

Таблица 1 – Вероятность загрузки диска при изменении радиуса

X — l2/l	1	3	5	7	9	11	13	15	17
P s	1,0	0,5	0,33	0,25	0,2	0,16	0,14	0,12	0,11

Взяв бесконечно малое приращение радиуса — 2 + A—2 и текущие значения радиуса X< — 2, можно продифференцировать равенство (9) и определить скорость изменения вероятности в зависимости от увеличения радиуса R2. Данные таблицы 1 показывают, что увеличение отношения R2 /R1 более чем в 4-5 раз не приводит к значительному росту вероятности использования полезной площади диска рушащего органа. Для натурной оценки полигона распределения семян по плоскости диска, согласно уравнению :

dP s         2

----—--— . dx      ( x + i ) ²

необходимо сохранить соотношение R₂ определить начальный радиус подачи R ₁.

Экспериментальная         проверка рекогносцировочные опыты показали,

/R1 и и что

технологический процесс получения крупы в вероятностном соотношении, при 99-100-процентном выходе продуктов переработки, можно описать потоком Эрланга 98-99 порядка.

Схема формирования потока Эрланга (потока просеивания) приведена на рисунке 2. Если считать, что каждое второе зерно на интервале (t, dt) (рис. 2) будет уходить из системы без обработки, то в этом случае формируется поток просеивания первого порядка, если каждое третье, то соответственно второго порядка. Тогда для потока 99-го порядка будет уходить в брак каждое сотое зерно.

Если суммарная интенсивность Л распадается на поток отказов и поток обработки продукта, то отношение интенсивности подачи к интенсивности ц отказов характеризуется параметром загрузки системы а а —X / ц.

Этот показатель определяет основные характеристики технологического процесса. Так, если уходит каждое второе зерно, система равновероятна. Задача состоит в том, чтобы в условиях производства технологической процесс и закономерности формирования потока зерна после шелушения удовлетворяли требованиям ведения рабочих процессов на предприятиях перерабатывающего комплекса. Для построения модели выходящего потока основной характеристикой является закономерность распределения интервалов между зернами в одинарном потоке.

Для одинарного потока длиной (t + dt), с площадью сечения dc2p , равной среднему размеру зерна, расстояния между зернами t1, t2, t3, ..., tn. Оно зависит от интенсивности потока и является ее обратной функцией.

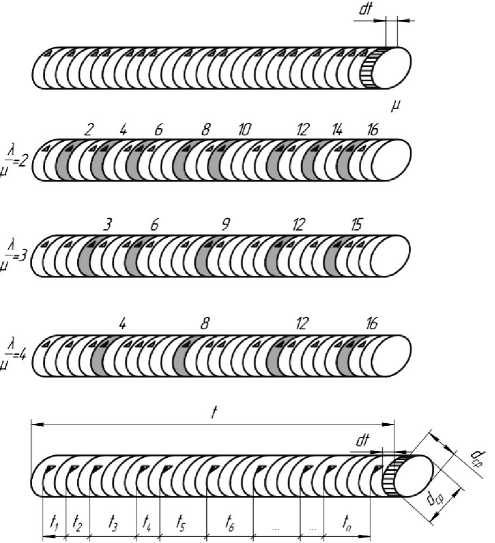
Рисунок 2 – Формирование потока Эрланга с отказами

Тогда расстояние равно сумме интервалов t 1 , t 2 , t 3 , ..., t n между зернами:

n t = 2 t n .

Вероятность распределения интервалов на полосе ординарного потока определяется по показательному закону:

P_k = Xe ^{-X t} .

Рассмотрим элементарный объем для интервала At :

V = d 2p -A t.

Тогда плотность распределения зерен в объеме (V + AV) при d cp = const будет определяться только размерами участка (t + At).

Вероятность попадания одного зерна на интервал At будет равна:

P 1 = X-At,                 (11)

а вероятность попадания k зерен на участке t:

P k ( t ^-(^T" e " ^{X t}.            (12)

k!

При отсутствии последействия вероятность попадания зерен на участок (t + At) равна произведению вероятностей P1 и Pk (t). Или, заменяя их значениями:

P - ( t + At ) = X-At М- e ^{-X t}.      (13)

k!

Переходя к пределу

P - ( t ) =

( Xt ) k k !

e t , получаем

уравнение плотности вероятностей распределения интервалов между зернами потока Эрланга k -го порядка. При k = 0 получаем показательный пуассоновский поток вероятностей:

P_k = Xe ^{-X t} .

Числовые характеристики потока Эрланга – его математическое ожидание, дисперсия и среднеквадратическое отклонение равны :

mk

k + 1

= 2 m o

= (k +1 ) -m o ;

D

_ k + 1 ^k = X ²

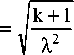
Таким образом, в потоке Эрланга статистические параметры выражаются через интервалы между зернами.

Для оценки интервалов между зернами в потоке Эрланга и определения функции распределения зернового потока необходимо решить уравнения:

^{-X t}

F k = 1 = ^e ;

F k = 2 = e ^{-X t} ( 1 + Xt ) ;

F k = 3

= e ^{-X t} 1 + X t + ^2 2!

^Fk = 4

= e -X t 1 +X , +M. + M

2!

3!

^{-X t}

F k = 5 = ^e

1 + X t +

( X t ) ²

2!

₊M ₊(X t ) l 3!       4!

F_k_ ₆= e -X t 1 + Xt+M. +&£ + M + M [             2!       3!       4!       5!

Ограничиваясь числом Эрланга для потока k-го порядка, функция распределения интервалов определяется по уравнению [8], [9], [10], [11], [12], [13]:

F k = 1 - R ( X ,k,t ) .

Тогда функция распределения интервалов между зернами определяется согласно уравнению (9), (10):

-it-k. Ж

F = ^{1 e :}r ( k - 1)-

Или, заменяя сумму степенным рядом для первых шести членов разложения, получаем:

F k = 1 - e ^{-X t}

1 +X t +

( X t ) ² ₊ (X t) 3 ₊(X t) l ₊(X t) 5

2!       3!       4!       5!

Уравнения показывают, что с увеличением порядка закона разделения смеси при шелушении интервалы, между зернами возрастают и приближаются к регулярному потоку с нулевой дисперсией. Поэтому lim D(t ) = k^^

X² ( k -1 )

а обработанный поток зерна с параметрами

— = const; D(t) = 0 ; k ^ ^ X стремится к регулярному, у которого расстояния между зернами равны между собой, т.е. поток становится более равномерным. При этом плотность вероятности распределения будет равна произведению вероятности появления зерна на интенсивность потока:

P k = ^ P ( k, x ,t ) .

С увеличением порядка потока отказов в работе рушащего органа плотность распределения интервалов между зернами в общем потоке уменьшается. Плотность распределения вероятностей расстояния между зернами определяется по уравнению и таблицам [1] пуассоновского распределения потоков.