Статистическая модель механической части электропривода подъема мостовых кранов

Механическая часть электропривода подъема мостовых кранов отличается сложностью и разнообразием конструкции, что делает конкретный расчет этой части крана весьма трудоемким и нерациональным. В то же время всеми авторами и разработчиками проектов признается существенное влияние упругих податливостей в механической системе на процессы в электроприводе подъема мостового крана. Одним из важнейших параметров, учет которых необходим при проектировании электроприводов мостовых кранов, является прогиб пролетных балок. Прогиб связан с рядом характеристик мостового крана, которые зависят от конструкции крана, режима его работы, времени нахождения в эксплуатации, длины пролетных балок, циклов нагружения и т. п. Влияние перечисленных показателей на величину прогиба достоверно не известно.

Целью настоящей работы является установление степени влияния перечисленных параметров на прогиб пролетных балок.

В качестве основного метода исследования был принят метод статистического анализа экспериментальных данных.

Основанием для анализа упомянутой зависимости, явились данные наблюдений по 38 мостовым кранам с различными техническими параметрами, важнейшими среди которых были: g_HOM -номинальная грузоподъемность, т; L_m - пролет крана, м; Т - возраст крана (отрезок времени от даты его производства до даты проведения испытаний), год и N - число циклов за время эксплуатации (под циклом понимается одна рабочая операция, включающая в себя подъем, перемещение и опускание груза). Величина прогиба пролетных балок мостового крана, Умм, рассматривалась как отклик системы на различные комбинации технических характеристик, перечисленных выше.

В процессе синтеза модели крана, описывающей зависимость величины прогиба его пролетных балок от эксплуатационных параметров, решались следующие стандартные статистические задачи:

• -    корреляционный анализ предикторов (эксплуатационных характеристик) с целью выявления линейных связей между ними [1,2];

• -    дисперсионный анализ предикторов с целью выявления наиболее значимых показателей [1,3];

• -    регрессионный анализ линейной зависимости прогиба пролетных балок мостового крана от эксплуатационных показателей, с целью получения расчетных соотношений [2, 3].

Все расчеты проводились с использованием пакета программ статистического анализа SPSS-15 [4, 5] (лицензия ГОУ ВПО ЮУрГУ L №071115 от 15 ноября 2007 года с продлением на 2008,2009 гг.).

Корреляционный анализ предикторов позволил установить, что все включенные в анализ переменные значимо коррелируют с переменной прогиб пролетных балок, однако, имеет место т. н. коллинеарность предикторов - переменные 5_Н0м, L_mTnN связаны.

Результаты регрессионного анализа представлены в таблице.

Таблица

Линейная модель для мостовых кранов представима в виде

Усынин Ю.С., Заляпин В.И., Бутаков М.С.

Y_mm = 7,877 + 0,062 ■ Q, + 0,352 • L_m -

• —О,088• T_vear -0,738- kod_cycl.

Здесь переменная cod _ су cl = N 10”⁵. Как видно из таблицы, значимыми переменными являются L_m и cod _ су cl . Именно они, в основном, определяют изменчивость переменной ¥_тт .

Значения множественного коэффициента корреляции (Л=0,74) и коэффициента детерминации (Л² =0,598) говорят о достаточно хорошей аккумуляции моделью информации, заключенной в исходных данных - модель аккумулирует около 60 % экспериментальной информации. Значение критерия Фишера (Г=Х2, 290) свидетельствует об адекватности регрессионной модели экспериментальным данным (уровень значимости менее 0,001).

Допустимая погрешность в величине прогиба мостового крана обычно определяется экспериментальным путем при нагружении крана предельно допустимым для него грузом и измерении величины прогиба. Нормативные документы не оговаривают величину допустимой погрешности при экспериментальном определении прогиба балки [6, 7]. Исходя из опыта проведения подобных экспериментов, допустимая погрешность определяется применяемой приборной базой и может быть принята АУ = ± 1 мм.

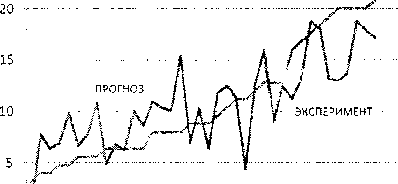
Можно считать эту величину вполне приемлемой при проектировании привода. С этой точки зрения интересно сравнить величину прогиба, прогнозируемую регрессионной моделью, с наблюдающейся экспериментально. На рисунке по оси абсцисс отложены номера мостовых кранов, упорядоченные по возрастанию величины наблюдаемого в эксперименте прогиба, по оси ординат -величина прогиба: экспериментальная и прогнозируемая регрессионной моделью. Анализ отклонений экспериментальных данных от прогнозируемых показывает, что, несмотря на верный качественный характер модели, в количественном плане модель нуждается в совершенствовании. Средняя абсолютная ошибка прогноза составляет 2,8 мм, средняя относительная - около 26 %.

Выводы

Методами статистического анализа показано, что величину прогиба мостового крана можно

Статистическая модель механической части электропривода подъема мостовых кранов

1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39

прогнозировать с помощью математической модели, представляющей собой уравнение множественной линейной регрессии. Наиболее значимыми факторами, определяющими величину прогиба, являются пролет мостового крана и количество циклов работы крана за срок эксплуатации. Остальные параметры (грузоподъемность и возраст крана) слабо влияют на модель.