Статистическая оценка индексов достоверности символов, формируемых в системе с мягким декодированием

Одним из наиболее эффективных направлений обеспечения требуемого качества цифровой передачи информации в условиях высокого уровня мешающих факторов является развитие средств помехоустойчивого кодирования и совершенствование алгоритмов декодирования корректирующих кодов.

Доказано, что декодеры таких кодов целесообразно строить с использованием мягких схем декодирования. Указанный подход обеспечивает повышение эффективности избыточного кода, обеспечивая энергетический выигрыш относительно жестких схем декодирования в пределах 2 дБ. Получение выигрыша приводит к усложнению решающего правила при обработке сигнала на выходе непрерывного канала связи. В мягком декодере каждый двоичный символ сопровождается индексом достоверности символа (ИДС), который в ряде источников определяется как оценка надежности информационного символа.

Принято считать, что с наибольшим эффектом ИДС могут быть применены в системах со сверточными кодами [1]. Вместе с этим, техноло- гические успехи в реализации больших объемов памяти привели к тому, что неалгебраическое (списочное) декодирование блоковых кодов стало объектом пристального внимания ряда исследований. В [2] показана возможность мягкого декодирования таких кодов за пределами их конструктивной корректирующей способности.

Известны несколько способов формирования ИДС:

• -    на основе логарифмического отношения функций правдоподобия [1];

• -    на основе квантования модулируемого параметра сигнала на несколько уровней – схема первого типа [1];

• -    на основе кортежа стираний в случае организации стирающего канала связи – схема второго типа [3].

Логарифмическое отношение функций правдоподобия обеспечивает не целочисленные значения ИДС, что отрицательно влияет на реализацию приемника. Но этот способ может быть легко связан со схемой первого типа, поскольку внутри кванта отношение функций правдоподобия является непрерывное оценкой.

Целью данной работы является статистическое моделирование процессов обработки сигналов с выработкой ИДС в канале с гауссовским шумом для схем первого и второго типов, получение для них сравнительных характеристик и выработка рекомендаций для реализации схем мягкого декодирования.

Выбранный класс модели для процедуры выработки ИДС во многом определялся трудностя- ми аналитической трактовки решающей схемы выполненной на основе стирающего канала связи.

Приводятся сравнительные результаты моделирования системы выработки ИДС по квантам и по кортежу стираний.

Постановка задачи

Пусть в месте приема наблюдается сигнал ^{z ( t} ) = s i ( t ) + ^{n ( t} ) ,                     (1)

где s i ( t ) - двоичный сигнал, принимающий при i = 1 значение двоичной единицы, а при i = 2 значение двоичного нуля, n ( t ) - аддитивная помеха, представляющая собой вклад гуссовского шума с нулевым средним и дисперсией σ ₀ ² .

Значение величины z ( t ) также будет случайной гауссовской величиной со средними значениями M ₁ > 0 и M ₂ < 0 в зависимости от переданного сигнала, при этом M ₁ = M ₂ В процессе детектирования сигнала принимается решение о том какая двоичная единица была передана. Это решение вырабатывается на основе сравнения z ( t ) с порогом, который в указанных условиях равен нулю.

Обычно выход демодулятора настраивается в виде жесткой схемы принятия решения относительно того, представляет ли условная вероятность p ( z | s 1 ) или p ( z | s ₂ ) значение ноль или единицу. В этой ситуации выход демодулятора квантуется на два уровня.

Полученную схему можно настроить таким образом, чтобы значение z ( t ) квантовалось на несколько уровней. Для этого в интервале значений от M _i до нуля назначается определенное число порогов. Интервалы нумеруются таким образом, чтобы наибольшему значению соответствовал интервал со значением |z(t)| «|M i|. В этом случае номер интервала служит ИДС, и логарифм отношения правдоподобия в интервале от M ₂ до M ₁ достигаетсвоегомаксимальногозначенияименно в точках |z(t)| = M J, а его минимальное значение определяется в точке |z( t )| = 0 . Если по указанной схеме назначить восемь интервалов, то индексы достоверности будут пронумерованы от 0 до 7, при этом интервал с ИДС имеющим номер 0 будет находиться возле точки z ( t )=0. Это справедливо как для положительных значений z ( t ), так и для его отрицательных значений.

Вместе с этим, для любой оценки существует вероятность неправильной идентификации принятого символа. Возникает вопрос: в какой мере полученным индексам достоверности следует доверять при обработке информации в декодере.

Необходимо отметить, что описанная схема получения ИДС не является единственной. В [3] предлагаетсядляэтихцелейиспользоватьстираю-щий канал связи. В таком канале назначается всего два порога, что упрощает конструкцию решающей схемы и способствует повышению скорости обработки информации в ней. Пороги выбираются как доля р от величины 2 M 1 , здесь 0 <  р < 1 . Следует отметить, что при таком подходе декодер не предназначен исправлять образовавшиеся в кодовой последовательности стирания, поэтому величина порога не ограничивается соображениями минимизации доли ложных стираний, а всего лишь обеспечивает наилучшее совпадение ИДС с правильно принятыми символами.

Для определения ИДС по кортежу стираний назначаются два скользящих окна размерам K ₁ и K ₂ битов каждое. При этом целесообразно принять K ₁ = K ₂ . Демодулятор, работая по жесткой схеме, образует поток информационных битов, в то же время в этом устройстве имеет второй выход, на котором фиксируется поток стираний

.. .x t + з ; x t + 2 ; x t + i ; x t ; x t - i ; x t - 2 ; x t -з . . в порядке возрастания номеров t . Обе последовательности между собой синхронизированы.

В потоке стираний не стертым позициям соответствуют нули, а стертым позициям соответствуют единицы. Окна следуют по потоку стираний одно за другим, перекрываясь между собой на интервале одного символа. ИДС вырабатывается для бита с номером t, попавшего в оба окна по принципу подсчета числа стираний в окнах K ₁ и K ₂ .

Первоначально каждому окну присваивается вес K _l + 1 , при l = 1 окно захватывает символы с уменьшающимся индексом t , одновременно с этим при l = 2 другое окно захватывает символы с увеличивающимися значениями t . Если в окно попало η _j стираний ( 0 ≤ y _j ≤ K _l ), то вес окна уменьшается на эту величину. Общая оценка R для символа определяется как сумма оценок первого и второго окна, но определяется по-разному для случая, когда оцениваемый символ стирание и когда такой символ принят без отметки стирания. Для стертого символа оценка определяется выражением:

t + 2 t

Rn = ^{( K} 1 ^{+ 1} - ^ ⁿ j ) ⁺ ( K 2 ^{+ 1} - ^ ⁿ j ) -¹ . (2) j = t j = t -2

Это увеличивает различимость оценок и обеспечивает повышение эффективности процедуры декодирования.

Для нестертого символа ИДС определяется как t+2                          t

R o = (K + 1 - ^ n j ) + (K 2 + 1" E n j ) ■ (3) j = t                     j = t -2

Легко проверить, что для R _n предельным значением является оценка 1 (все символы в окнах стерты), а для R ₀ – оценка 8 (среди символов, попавших в окна, нет ни одной единицы). Такая нумерация легко переводится в трехразрядные ИДС с номерами от 0 до 7. Следовательно, имея для обоих вариантов построения решающей схемы одинаковый набор оценок, легко получить сравнительные характеристики для каждого значения ИДС.

Актуальным является разработка такой решающей схемы, которая обеспечивала бы лучшее совпадение высоких оценок с правильно принятыми символами с целью обеспечения эффективной работы мягкого декодера избыточного кода.

Описание моделей демодуляции

Модели демодуляции и образования ИДС разработаны для противоположных сигналов в системе MATLAB, при этом область оптимального решения для таких сигналов определяется выражением:

min{| z ⁽ t ) ^- M J 2 ^- N о In PVmi ]},         (4)

где z(t) - уровень принятого сигнала, Mi - мате- матическое ожидание номинального уровня сигнала, N0 - спектральная плотность мощности белого шума, Pmi ] - априорная вероятность i-го сигнала [4].

Таким образом, ошибки при передаче M1 воз- никают тогда и только тогда, когда составляющая шума n(t) превышает значение d /2, где d- расстояние между сигналами M1 и M2 .

Если сигналы имеют минимальную энергию и, следовательно, являются противоположными, то длина каждого вектора 4Mi , так что d = 24Mi

и

/ I- . , A ^M"

P [ M ] = Q

⎜ N ⎟

⎝     0⎠

для двух равновероятных противоположных сигналов, где q ( - ) - гауссовый интеграл ошибок.

Изменяя значение N0 = 2σ 2 , получаем зависимость вероятности ошибки на бит как функцию параметра отношения сигнал-шум:

M i- дБ = 10lg M

^N 0         ^N 0

Поток исходных двоичных сигналов формируется датчиком случайных чисел с равномерной плотностью распределения вероятностей (ПРВ). Взависимостиот Mi датчикомснормальнойПРВ формируется значение z(t), которое подвергается проверке по правилу решающего устройства (первого или второго типа). Принятое решение сверяется с данными, полученными от датчика с равномерной ПРВ. Для достижения требуемой статистической погрешности в модели формируется не менее 106 битов. Данные о правильно принятых символах и ошибках накапливаются в счетчиках отдельно для каждой оценки.

Следует указать, что в случае z ( t ) >  M 1 и z ( t ) <  M 2 принятый символ получал ИДС равный 7, то есть решающее устройство моделировалось по принципу ограничителя с кусочно-линейный преобразованием, имеющем характеристику [5]

⎪- M2 при z(t) ^ m 2; z(t) = • zi (t) при M2 < z(t) < M 1; (7) ⎪M1 при z(t) > M1, здесь z1 (t) - символ принятый с i-м ИДС, причем 0≤i≤7.

В схеме первого типа расстояние d разбивается на 16 интервалов, которые нумеруются в возрастающем порядке от точки пространства сигналов z(t) = 0 до M по восемь значений для положительных и отрицательных z ( t ).

В схеме второго типа для каждого такта учитывалась последовательность пяти текущих битов. Обозначим символ стертый в момент времени t в кортеже стираний через x t .

Если на приемной стороне образовалась последовательность символов, пронумерованная относительно анализируемого символа x t по оси времени влево и вправо, тогда в правое окно при K 1 = 3 попадают символы x t ; x t -1 ; x t -2, , а в левое окно K 2 - символы X t + 2 ; X t + 1 ; X t , как показано на рис. 1.

2 .2 .2 2 2 .2 .2.„ Xt + 3 ; Xt + 2 ; Xt +1; XL ; Xt —1; Xt —2 ; Xt —3 ... ■

Рис. 1. Пример анализа стертых позиций

После оценивания символа X t , при получении очередного значения x t _{+ 4} , приемник одновременно сдвигает окна влево на такт, захватывая x t +4 , и оценивает символ x t +4 описанным способом. Символ x t - 2 на этом шаге из анализируемой последовательности удаляется. Установлено, что в такой схеме оценки меньшего веса сопровождают стертые позиции и могут служить ИДС для синхронизированных с ними символов информационного потока.

При организации стирающего канала связи условие (7) исключает контроль параметров модулируемого параметра по максимуму [6] и фор- мирование сигнала стирания при достижении z(t) > Mi| . Это в наибольшей степени соответствует принятым принципам построения решаю- щих схем.

В ходе моделирования стирающего канала связи изучался вопрос влияния на ИДС интервала стирания, задаваемого параметра ρ . В модели этот параметр изменялся от значения р = 0,1 до значения р = 0,7 с шагом 0,1.

Условная ПРВ двух гауссовских сигналов s1 и s2 показывает, что значение вероятности ложного стирания pf.s. при симметричном ин- тервале стирания и передаче s1 в условиях гауссовских шумов всегда будет превосходить значе- ние вероятности правильного стирания pt.s. :

j p(z | s i ) dz <

-ρ

ρ jP(z I si)dz .

Аналогичный результат получается в предположении, что передавался сигнал s ₂ . С увеличением интервала стирания ρ отрицательный эффект p f _.s. усиливается. Наличие в потоке стираний ложных решений о стираниях снижает эффективность схем второго типа и меру их влияния на ИДС можно установить только в ходе моделирования.

Результаты моделирования

Результаты моделирования системы выработки ИДС первого типа приведены на рис. 2. Для каждой оценки в ходе моделирования были получены частость совпадения этих оценок с ошибочно принятыми символам N ⁱ _f и частость совпадения с правильно принятыми символами N _t ⁱ .

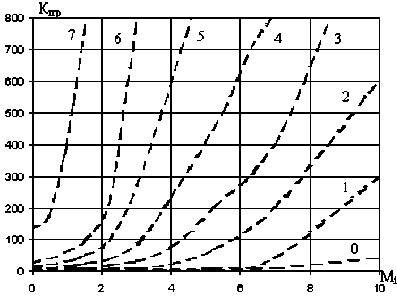
Рис. 2. Отношение правдоподобия ИДС для метода квантования

В отдельности указанные характеристики не дают полной вероятностной картины. Для более наглядного представления полученных результа- тов для одинаковых i было выбрано отношение правдоподобия

i

K пр = _N^N _i ^t _f .                    (9)

и построены зависимости K пр ( M i / N 0 ) .

Графики показывают, что отношение правдоподобия для оценок 7 и 6 резко возрастает даже при низких отношениях сигнал-шум. Для других оценок этот показатель монотонно увеличивается по мере роста энергетики сигнала относительно шума, но для этих оценок характерен едва заметный рост значения K _пр даже при относительно хороших условиях приема сигналов. Как и следовала ожидать, ИДС от 0 до 3 не могут быть однозначно использованы декодером для качественного декодирования кодовых комбинаций избыточного кода. Символы с такими оценками требуют проверки и восстановления.

Длясистемывторого типапри значении p = 0,1 результаты моделирования приведены на рис. 3. Заметно, что ИДС в зависимости от отношения сигнал-шум образуют два семейства оценок. При этом поведение индексов с оценками 7 и 6 заметно хуже относительно метода разбиения на кванты. В семейство высоких оценок попадает оценка 2. Это объясняется редким, но возможным для гауссовского канала сочетанием стертых позиций, на коротком интервале времени, когда в оба окна попадают до 4 стираний. Учитывая низкий вес такой оценки, декодер однозначно не должен использовать ее без дополнительной проверки в ходе восстановления кодовой комбинации.

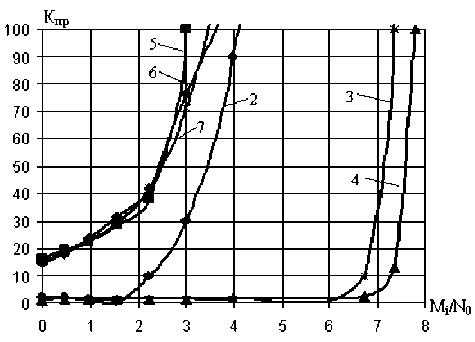
Рис. 3. ИДС при интервале стирания 0,1

При увеличении интервала стирания поведение ИДС становится более отчетливым. Например, при р = 0,7 оценки от 7 до 5 формируют вполне обособленную группу, имеющую резкий рост коэффициента правдоподобия в пределах отношения сигнал-шум от 1 до 2 дБ. Характеристики ИДС для данного случая приведены на рис. 4.

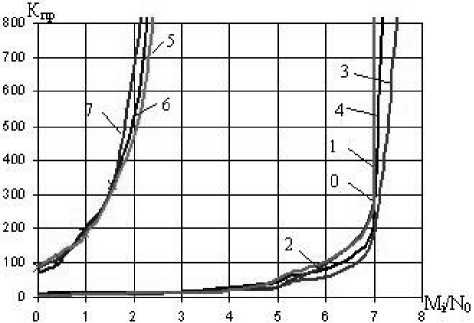
Рис. 4. ИДС при интервале стирания 0,7

В традиционной схеме со стиранием элементов введение указанного интервала недопустимо из-за резкого роста p f.s. .

В рассматриваемой схеме приема подобный подход дает положительное решение: оценки с высокими ИДС образуют обособленное семейство, в то время как, оценки с худшими ИДС формируют свою группу, сильно проигрывающую по отношению сигнал-шум первой. Анализ полученных результатов указывает на то, что символы с низкими ИДС могут быть использованы декодером как стирания, но в отличие от классической схемы эти стирания имеют вес, указывающий на степень группирования стертых позиций на длине окон анализа.

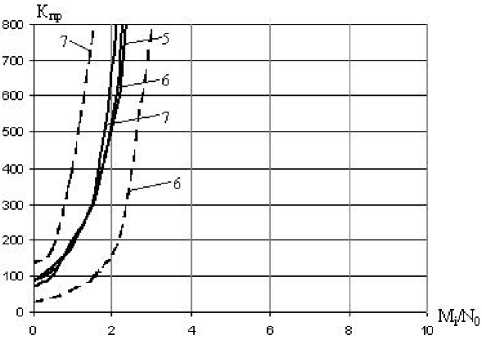
Рис. 5. Сравнение ИДС для схем первого (пунктир) типа и второго типа пределены по диапазону Mi / N0 , а для второй схемы различия для оценок 7, 6 и 5 практически незаметны. Это обеспечивает снижение сложности декодера, поскольку такие оценки могут быть приняты за один показатель с высоким ИДС. Оценки от 4 до 0 декодер восстанавливает, считая такие символы принятыми с высокой вероятностью ошибочно.

Общие данные для схем первого типа (пунктир) и второго типа приведены на рис. 5.

Выводы

Использование стирающего канала связи обеспечивает также как и в методе квантования целочисленные значения ИДС.

Применение в решающей схеме стирающего канала связи обеспечивает всего два порога сравнения, а метод квантования требует решения как минимум 8 неравенств. Снижение числа порогов упрощает реализацию решающей схемы.

Наиболее важной особенностью формирования ИДС по кортежу стираний является резкий рост отношения правдоподобия для оценок от 7 до 5 при большом интервале стирания и малом отношении сигнал-шум. Это способствует повышению эффективности процедуры мягкого декодирования за счет лучшего различения гипотез о принятом кодовом векторе.