Статистическая оценка вероятности правильного обнаружения веществ в ИК Фурье-спектрометрии

Проблема дистанционного контроля загрязнения атмосферы, а также химического контроля воздушной среды промышленных и других важных объектов на сегодняшний день является достаточно актуальной. Причиной этому служит всё больший рост числа загрязняющих веществ, а также производств, выбросы которых не удаëтся определить в непосредственном контакте. Вследствие этого уже более двух столетий ведутся разработки по созданию технологий и методов бесконтактной идентификации. Одним из характерных свойств, являющимся сугубо индивидуальным для каждого вещества, является оптический спектр, что позволяет использовать его как некий идентификатор. Одним из распространëнных методов получения спектров веществ является инфракрасная (ИК) спектрометрия. Выбор именно ИК-области обусловлен тем, что излучение этого диапазона возбуждает колебательное движение молекул или их отдельных фрагментов, вследствие чего происходит ослабление интенсивности только на частотах колебаний молекул, поэтому спектры каждого из веществ являются уникальными, а линии спектра селективными и ярко выраженными.

ИК-спектрометры разделяются на дифракционные и фурье-спектрометры на базе интерферометров. В данной работе будет рассмотрен второй класс приборов, однако описанные методы можно применять и для дифракционного метода. Особенностью фурье-спектрометров является возможность работы с более низкими интенсивностями [1] нежели в дифракционных установках, что позволяет детектировать спектры собственного излучения.

Важной задачей, возникающей при разработке ИК фурье-спектрометра, является выбор способа иден- тификации вещества по восстановленному спектру. Разумеется, возможен анализ химического состава по наличию некоторых характерных полос в спектре, однако более надëжным и точным методом является последовательное сравнение полученного спектра со спектрами уже известных веществ, хранящихся в базе данных эталонных спектров. Очевидно, что идентифицируемый сигнал может быть значительно зашум-лëн, что ещё сильнее усложняет ситуацию. В настоящее время известно множество различных методов и средств решения задач распознавания, таких как: обучаемые нейронные сети [2], использование нечëт-кой логики [3], методы PCA (principal component analysis) [4], а также введение различных мер схожести между данными [5– 11]. Основные работы по поиску и сравнению спектров веществ в базе данных были сделаны Клерком [12] и Луинджи [13]. Также фундаментальная работа по расчëту мер схожести в базе данных была проделана в [14]. Одной из возможных мер схожести является статистический коэффициент корреляции Пирсона [15] (здесь и далее будем считать, что спектры представлены в виде числовых векторов конечной длины):

( x ^- x ^{) T}( y ^- y )

• ■ II x - x llll y - y l ’                                       ^(}

где x, y - векторы сравниваемых спектров, x - среднее арифметическое компонент вектора x , ||x || - евклидова норма вектора.

Здесь и далее выражение x - x означает вычитание из всех компонент вектора одинаковый скаляр.

Известно, что r ∈ [-1,1], причëм равенство единице достигается только если сигналы линейно зависи- мы, что в случае спектров даëт повод говорить об их идентичности. Чем менее «схожи» спектры, тем ближе величина (1) к нулю. Заметим, что из стремления (1) к единице следует стремление нормы разности спектров к глобальному минимуму. В работах [16– 22] описан метод идентификации по коэффициенту корреляции: сначала величина (1) рассчитывается для исследуемого спектра со всеми спектрами из базы данных, далее выбирается вещество с максимальным коэффициентом корреляции, и если (1) превысили заранее заданный эмпирический порог, то вещество считается идентифицированным.

1.    Вероятностные характеристики коэффициента корреляции

Фишер и Кенни в [23, 24] получили точное теоретическое выражение для функции плотности вероятности коэффициента корреляции Пирсона в случае, когда сравниваются две случайные величины с двумерным гауссовым распределением в известной корреляции. Существенным ограничением является то, что оба вектора должны быть случайными. В свою очередь, при идентификации по базе данных в ИК фурье-спектрометрии эталонные спектры могут считаться точно известными, так как были получены в лабораторных исследованиях путëм множественных усреднений. Также невозможно заранее знать вероятностный коэффициент корреляции без набора множественной статистики.

Предположим, что исследуемый вектор зашумлëн белым аддитивным шумом, имеющим нормальное распределение, тогда итоговый спектр будет иметь такие же характеристики шума из-за свойств преобразования Фурье. То есть исследуемый спектр может быть представлен в виде:

т   т*   т     т   т*

x =τ +ξ , y =τ ,                           (2)

где т*- вектор эталонного спектра, ^ - шумовой вектор, каждая компонента которого имеет нормальное распределение с известными характеристиками N(0,σξ2).

Обозначим через r j коэффициент корреляции спектра X с веществом из базы данных под номером j = 1,..., M , где M – число веществ в базе данных. Будем считать, что база включает в себя вещество со т спектром τ , и пусть его номер j .

Получим явное выражение для коэффициента корреляции в случае, когда спектр X сравнивается со спектром т * . Подставив (2) в (1), получим:

_* r^j

σ ˆ _τ * + σ_ξ r _ξ ^{j *} σ ˆ _τ ² * + δ ² + 2 σ ˆ _τ * σ_ξ r _ξ ^{j *}

-    II т* —т*|2

где σ ² * =          – среднеквадратичное отклонение

т*

спектра τ , характеризующее его интенсивность,

*

^j r _ξ

ЛT ( т * -т * )

N σ σ ˆ ξ _τ

– коэффициент корреляции чистого шума с эталонным спектром т * ,

_δ 2 ₌ ξ-ξ ² N

среднеквадратичное отклонение шума,

N – число точек в экспериментальном спектре.

Видно, что r ^{j *} является функцией от двух случайных величин (4) и (5), имеющих нормальное и хи-квадрат распределения соответственно. Точный анализ функции (3) в этом случае представлен в [25]. Однако можно воспользоваться тем фактом, что в рассматриваемых спектрах число N достаточно велико (обычно от 200 до 800) для того, чтобы рассматривать выражение (5) как точечную оценку дисперсии σ_ξ ² . Заметим, что в знаменателе (3) складываются

δ ² и величина 2 σ ˆ _τ * σ_ξ r _ξ ^{j *} . Если принять δ ² = σ_ξ ² , то

(2 N - 2) σ_ξ ⁴ ошибка такой оценки будет составлять

N ²

*

[26], а дисперсию величины 2 σ ˆ _τ * σ_ξ r _ξ ^j можно полу-

4 σ_ξ ² σ ˆ ² *

чить по теореме о сумме случайных величин:    N ^τ

Если выполнено условие

(2 N - 2) σ_ξ ⁴ N ² σ ˆ 2_*

^    » 0,5

^σ ξ ²

4 σ ² σ ˆ ²

« — ^

-

N

1 2 N

,

то можно принять величину δ2 за детерминированную и равную σξ2 . В левой части выражения (6) сто- ит отношение сигнал/шум (SNR). Таким образом, условие (6) можно интерпретировать как требование значительного превышения уровня сигнала над уровнем шума.

С учëтом (6) выражение (3) может быть представлено в виде:

SNR + r ξ ^{j *} r^j =                             _*

SNR + 1 + 2 SNR r _ξ ^j

.

Сходный результат был получен в [27], однако при учëте того, что r _ξ ^{j *} ≡ 0 , что возможно только при N →∞ .

Коэффициент корреляции (7) является функцией только одной случайной величины с известным рас- пределением:

w ( r _ξ ^{j *}) =

N 2 π exp

(т С И ^

/

С использованием функции (8), могут быть полу- чены моменты всех порядков.

Для случая j ^ j * коэффициент корреляции за-

пишется в виде

r^j _

*

r^Jj ^SNR + r j

' SNR + 1 + 2 4SNRr^' ’

Математически вероятность такого события запишется следующим образом

P correct _ P [ ( r j * >  J V j * j * ) Л ( r ^J * >  r * ) ]         (11)

где введено r

* _ ( T ^j -T ^j ) T ( T - T * )

Рассмотрим отдельно каждую из скобок. Подставим в (11) полученные ранее выражения (7) и (9), тогда

^T j -

t ^j |K -*1 ’

r _s ^J определяет

ся аналогично (4), но для спектра т ^J , T ^J - эталонный спектр вещества j в базе данных.

Функция (9) зависит от двух случайных величин, причëм стоит учитывать, что эти величины не являются независимыми. Чтобы найти их совместное распределение, нужно знать корреляционную функцию шума. Примем, что шум является некоррелированным (S i S j / _ о ^ 8 ij , где 8 ij - символ Кронекера. Тогда с учëтом (8) ковариация коэффициентов корреляции запишется

*** jj jj j j cov^ , г ) ^_ \ г , г ^ ) \ ^ /\ г ) ^_

_ ( Т * -T * ) T ( ^{т J} -T ^J )_ r^{J                         (10)}

_    N 2о .д,    _ N ’ т тJ а вероятностный коэффициент корреляции будет равен r jj* .

Таким образом, получены упрощëнные формулы для коэффициентов корреляции (7) и (9), а также найдены свойства случайных величин, входящих в них.

2. Правильное обнаружение вещества

Поскольку исследуемый спектр является зашумлённым, не всегда удаëтся правильно идентифицировать вещество. Возможны случаи, когда, например, будет идентифицировано другое вещество, либо когда сигнал будет расценён как чистый шум и пропущен. На практике необходимо знать, с какой вероятностью было произведено обнаружение. Конкретизируем понятие правильного обнаружения.

Пусть исследуется спектр X вещества j * из базы данных. Тогда обнаружение считается правильным, если коэффициент корреляции r ^{j *} превысил коэффициент корреляции со всеми другими веществами, и к тому же превысил некоторый заранее заданный порог r_j * .

(      ² ( 1 - r ^1y )

1 + r ²¹¹

-

Е

N

( r +

r 1 j ^*

)

1 - r^1f

1 + r ^1,2 - ( r ^{1 J} + r ^{2 J} )

2 ( 1 - r^2j* )

1 - r^2j*

Совместная плотность вероятности для вектора Л будет иметь вид

w ( Л )      1---- exp I - ¹ Л T ЕЛ

,п е I ²

r( - r { > SSN R ( r j - 1 ) .

Введем величину Ф j :

*

^ф * ^{_ r} ^ ^j

j r^

S T ( т * -T * ) S T ( T j -T j )

N o_Ed, ^S T

N o_Ed ,

S T ^J

.

Из формулы (11) видно, что вероятность правильного обнаружения можно представить как функцию

только одного

Л _ { ф_р Ф 2 , ^ ,Г²’, ^ ,

случайного

вектора

Ф M } , имеющего длину M (чис-

ло веществ в базе данных), и на позиции j ^* стоит величина r ^ ^J * . Видно, что все компоненты вектора Л статистически зависимы и вместе подчиняются многомерному Гауссову распределению. Чтобы найти их совместное распределение, построим ковариационную матрицу для величин Ф i и Ф j . Воспользуемся условиями из (10) для корреляции шума, тогда

cov ( ф i , Ф * ) _

/ .л -л \

1 + r i - ( r i + r^J )

где i , j ^ j *.

Ковариация величин

/ j * _ \ 1 - r^JJ cov r , Ф , _------.

\ ^{S J}) N

N

,

*

r ^ ^j и Ф j будет равна:

.

Рассмотрим выражение во второй скобке Подставив (7), получим: *

V SNR + r _S ^j SNR + 1 + 2^ SNRrS"

*

= >  r, .

*           j ^*

в

Обозначим верхнее и нижнее решение этого выражения относительно r ^ ^J как Г up и Г _down соответственно.

Совместив (13) и (14) и с учетом формулы (8), получим итоговую ковариационную матрицу:

1 - r ^{1 j *}

1 - r

2 j ^*

••

В итоге вероятность (11) может быть найдена как интеграл от (15) по области допустимых значений:

Pcorrect _ J W(Л) dЛ ,(16)

Г

где Г - область, ограниченная Г up , Г down и неравенством (12).

Опишем кратко полученный алгоритм расчёта вероятности правильного обнаружения:

• 1.    Исследуемый спектр последовательно сравнивается со всеми веществами из базы данных.

• 2.    Выбирается вещество, коэффициент корреляции с которым оказался максимальным.

• 3.    Если максимальный коэффициент корреляции превысил эмпирический порог, то вещество считается идентифицированным.

• 4.    Запоминается номер идентифицированного вещества.

• 5.    По этому номеру строится ковариационная матрица X и находятся границы области значений Г .

• 6.    По формуле (16) находится вероятность правильного обнаружения.

3.    Экспериментальная проверка

Для проверки полученных результатов были проведены численные эксперименты с реальной базой данных спектральных коэффициентов пропускания, состоящей более чем из 50 спектров. Численное моделирование проводилось в MATLAB путём генерации случайных величин с последующим расчëтом различных статистических характеристик. Обычно эксперимент повторялся 1000 – 10000 раз с различны- ми веществами и статистически находились несме-щëнные вероятностные оценки математического ожидания.

На рис.1 изображено сравнение теоретических средних значений, полученных по формулам (7) и (9), с математическими ожиданиями коэффициента корреляции (1) (на рисунке показаны точками). Видно хорошее совпадение результатов, что говорит о применимости оценки (6) для расчётов моментов первого порядка. Далее, на рис. 2, показаны эксперименты по расчёту среднеквадратичного отклонения в сравнении с дисперсиями коэффициентов корреляции для двух пар тестовых веществ. Однако, в этом случае уже наблюдается расхождение при низких значениях отношения «сигнал/шум».

Из (15) и (16) видно, что для расчëта вероятности правильного обнаружения необходимо вести интегрирование по области очень большой размерности (в данном случае dim(Г) = 58 ). Этот факт существенно замедляет скорость работы реальных систем и полностью исключает возможность работы в режиме реального времени. Однако в ходе численных экспериментов было установлено, что в качестве оценки величины (16) может выступать математическое ожидание вероятностей превышения коэффициента корреляции rj над всеми остальными r j :

Р , correct

= — У Р ^ >  г M ^ ⁽

j ) P ( r j >  j ) ,

причём каждая вероятность в сумме (17) выражается через функции ошибок:

P ( rj * > rj ) = 2 X

^X erf

I

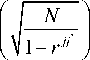
+ erf

*

N • SNR (1 - r j )

V 4

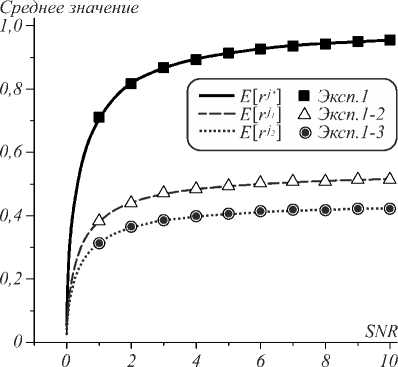
Рис.1. Зависимость среднего значения E [ r ^j ] коэффициента корреляции от отношения «сигнал/шум»

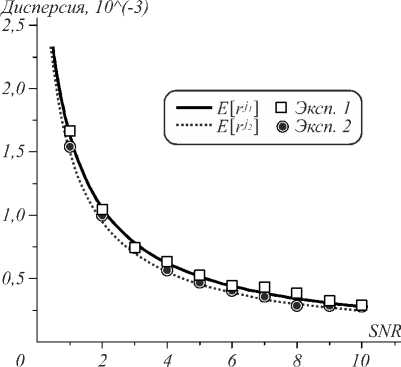
Рис.2. Зависимость дисперсии D [ r ^j ] коэффициента корреляции от отношения «сигнал/шум» SNR

Результаты сравнения (17) с экспериментом показаны на рис. 3. Каждая экспериментальная точка просчитывалась 1000 раз и затем усреднялась. Результаты совпадают даже для низких значений «сигнал/шум». Для случая SNR > 1 для всех веществ показано, что вероятность события r j * <  r j крайне мала. Поэтому решающую роль играет правый множитель в (17):

Г up ( r j* , SNR )

P ( r j * >  r j * ) =      j     w ( r i * ) d r(.                (19)

г down ( r j* , SNR )

Выражение (19) удаëтся представить через неэлементарные функции, однако запись является слишком громоздкой, чтобы приводить её в статье. Заметим, что с помощью (19) можно находить пороги для заданной вероятности правильного обнаружения. Хотя зависимость r** (Pcorrect) не выражается явно, опреде- ление порога обнаружения при заданной вероятности может вестись с помощью алгоритма интерполяционного поиска, так как P(rj**) является монотонно убывающей функцией. Трудоëмкость такого алгоритма [28] можно оценить как O(log2 [log2 (1/ε)]) , где ε – допустимая погрешность. Этот результат даёт возможность находить пороги обнаружения веществ при различных отношениях «сигнал/шум», гарантируя заданную вероятность правильного обнаружения (рис. 4).

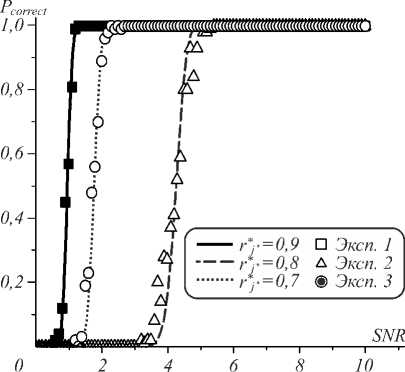
Рис. 3. Вероятность правильного обнаружения Pcorrect от отношения «сигнал/шум» SNR

Заключение

В работе рассмотрен метод определения вероятностных характеристик коэффициента корреляции Пирсона в случае, когда один из сигналов имеет аддитивную добавку из гауссовского δ-коррелиро-ванного шума, а другой является незашумлëнным. Данный метод предлагается применять для идентификации веществ по их спектрам в фурье-спек-трометрии. Основное допущение метода основывается на замене величины с распределением хи-квадрат на еë статистическую оценку. Показано, что такое приближение применимо при больших отношениях сигнал/шум.

На основе полученных вероятностных характеристик введено понятие вероятности правильного обнаружения вещества и найдено явное теоретическое выражение для этой вероятности. Также найдены уп-рощëнные выражения, позволяющие находить вероятность гораздо быстрее при численном расчёте.

Показано, что вероятность правильного обнаружения зависит от порогового коэффициента корреляции, который ранее определялся эмпирическим путём. Предложена методика, позволяющая находить порог обнаружения по заданной вероятности правильного обнаружения и отношению сиг-нал/шум.

Разработанные методы проверены на реальной базе данных спектров веществ, состоящей из 58 веществ, и показана применимость предложенных методов при выполнении введëнных приближений.

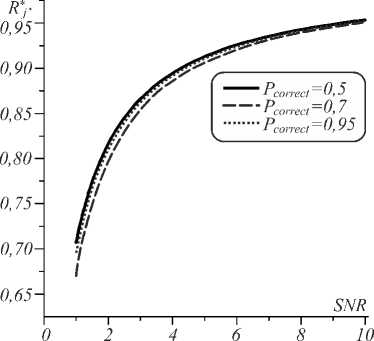
Рис. 4. Пороговый коэффициент корреляции в зависимости от отношения «сигнал/шум» SNR для заданной вероятности правильного обнаружения