Статистические характеристики двоичных псевдослучайных сигналов, формируемых на основе систем Дмитриева-Кислова и Анищенко-Астахова

Нелинейные системы с динамическим хаосом используются в качестве формирователей сигналов для систем широкополосной связи. Наряду с принципиально новыми подходами к формированию сигналов на основе нелинейного подмешивания, сверхширокополосных хаотических радиоимпульсов системы с динамическим хаосом могут применяться в качестве формирователей двоичных псевдослучайных последовательностей [1]. В [2-3] были рассмотрены двоичные последовательности, формируемые на основе систем Лоренца и Чуа. Наряду с данными системами в настоящее время широко исследованы системы ДК и АА, описывающие поведение радиоэлектронных схем с хаотической динамикой. Рассмотрение последовательностей, сформированных на основе данных систем, позволит уточнить их место в ряду иных известных последовательностей.

Автокорреляционные функции (АКФ) являются одними из наиболее информативных характеристик псевдослучайных сигналов. Снижение интервалов корреляции АКФ двоичных псевдослучайных сигналов является важной задачей для систем широкополосной связи и криптографических систем. Исследования показали, что улучшение характеристик формирователей сигналов на основе нелинейных систем с динамическим хаосом возможно за счет введения квазирезонансных управляющих воздействий на параметры систем и параметры временной дискретизации [3].

Целью работы является анализ статистических характеристик двоичных псевдослучайных сигналов, сформированных на основе нелинейных систем ДК и АА с динамическим хаосом в условиях квазирезонансных воздействий на параметры временной дискретизации.

В качестве объекта исследования в работе выбраны системы АА:

X = mX*Y-XZ ,Y = -X;

Z = -gZ^-\QCY           (1)

и ДК:

TX + X = MZ exp(-Z²);

Y = X-Z , Z = Y-Z/Q,        (2)

описывающие поведение ряда радиоэлектронных схем с хаотической динамикой. В (1)-(2) X,Y,Z – пространственные переменные нелинейных систем с динамическим хаосом; m,g – параметры системы АА, 1(A2 – ступенчатая функция Хэ-висайда; T,M,Q – параметры системы ДК [1].

Формирование двоичных псевдослучайных последовательностей на основе систем (1), (2) проводилось по методике [2] путем сравнения исходных реализаций с пороговым уровнем, равным медиане сигналов X,Y,Z. Период сравнения выбирался близким интервалу корреляции исходного хаотического сигнала. В процессе формирования сигналов использованы значения параметров систем АА m = l,g = 0,6 и ДК T = 2,M = 7,2 = 10 . Параметр численного интегрирования систем (1)-(2) K , определяющий отношение периода квазирезонансных колебаний к шагу численного интегрирования систем, выбирался не менее К = 500.

Погрешности по равновероятности появления в двоичных последовательностях символов «0» и «1» являются одними из наиболее часто рассматриваемых их характеристик. В работе получены оценки погрешности, равные разности вероятностей появления символа «1» и символа «0».

На рис. 1 приведены распределения последовательностей в зависимости от погрешности по равновероятности. Из рис. 1 видно, что погрешности по равновероятности для последовательностей двоичных чисел, сформированных на основе системы (1), ниже, чем погрешности для системы (2).

Автокорреляционные функции сигналов характеризуют внутреннюю связность символов в последовательностях. Оценка автокорреляционных функций двоичных последовательностей традиционно сопровождается оценкой максимального уровня боковых лепестков [1].

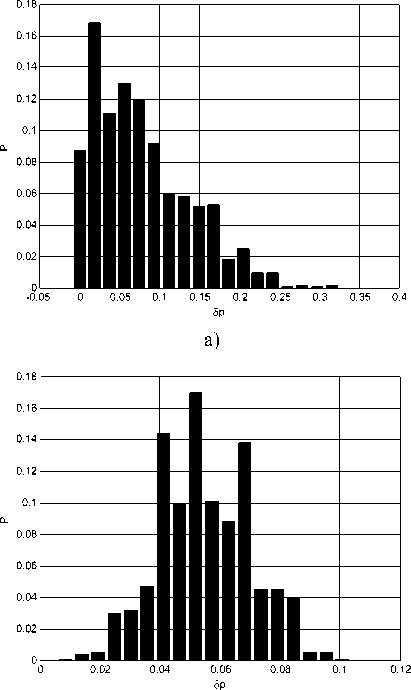
б)

Рис. 1. Гистограммы последовательностей в зависимости от значения погрешности по равновероятности: а) система (1), б) система (2)

Проведенный анализ показал, что для систем (1) и (2) максимальный уровень боковых лепестков АКФ не превышает 0,27. В системе (1) можно отметить наличие последовательностей с уровнем боковых лепестков АКФ от 0,12 до 0,26; но общая доля таких последовательностей в исследуемом массиве не более 5%. Снижение интервалов корреляции двоичных псевдослучай- ных сигналов является одной из основных задач в формирователях двоичных псевдослучайных сигналов. Одним из видов управляющих воздействий на параметры нелинейных систем и параметры временной дискретизации являются квазирезонансные воздействия вида [4]

m(O = m_o(l + W^Y (3)

где т^ и m_Q – мгновенное и начальное значения выбранного параметра системы, f (0 – функция, определяющая форму воздействий, M – коэффициент, влияющий на глубину модуляции параметра системы.

С целью исследования влияния глубины модуляции воздействий вида (3) на корреляционные характеристики сигналов систем (1), (2) были получены распределения вероятностей интервалов корреляции для TV = 1000 реализаций двоичных чисел по 512 бит при вариации глубины модуляции M . Формирование двоичных сигналов на основе систем (1) и (2) выполнено при вариации начальных условий систем. В качестве модулируемого параметра выбран параметр временной дискретизации, показавший высокую эффективность в управлении корреляционными характеристиками хаотических сигналов [3; 5].

В таблице 1 приведено распределение последовательностей, сформированных на основе системы АА, в зависимости от глубины модуляции M по значениям интервалов корреляций.

Таблица 1. Распределение последовательностей, сформированных на основе системы АА

Глубина модуляции м	Доля последовательностей с интервалом корреляции, %
	3	4	5
0	0	0	100
0,33	0	100	0
0,50	22	78	0
0,67	100	0	0
0,75	100	0	0

Из таблицы 1 видно, что увеличение глубины модуляции приводит к пропорциональному изменению интервалов корреляции. Увеличение глубины модуляции параметра временной дискретизации (1) приводит к сокращению интервала корреляции с 5 (для M = 0) до 3 (для M = 0,75).

В таблице 2 приведено распределение последовательностей, сформированных на основе сис- темы ДК, в зависимости от глубины модуляции M по значениям интервалов корреляций.

Таблица 2. Распределение последовательностей, сформированных на основе системы ДК

Глубина модуляции М	Доля последовательностей с интервалом корреляции,%
	1	2	3	4
0	0	0	83	12
0,05	0	0	86	1
0,13	0	1	90	0
0,20	0	0	100	0
0,29	0	24	43	0

Из таблицы 2 видно, что без квазирезонанс-ных воздействий интервалы корреляции последовательностей на основе системы (1) равны 3. Глубина модуляции параметра временной дискретизации системы (2) M может меняться в меньших пределах по сравнению с системой (1), а также по сравнению с системой Лоренца и Чуа. При M = 0,29 среди последовательностей появляются интервалы корреляции 2, но при этом среди последовательностей появляются интервалы корреляции порядка 10. Поэтому дальнейшее увеличение глубины модуляции M > 0,29 становится нецелесообразно.

По таблицам 1-2 можно отметить то, что несмотря на применение модуляции параметра временной дискретизации интервалы корреляции последовательностей, сформированных на основе (1)-(2), не достигают интервалов корреляции M -последовательностей. В системе Лоренца при максимальной глубине модуляции M = 0,8 половина последовательностей ансамбля может иметь интервал корреляции 1, в системе Чуа практически все последовательности ансамбля обладают интервалом корреляции 1 [6].

Максимальный уровень боковых лепестков АКФ является дополнительной оценкой, характеризующей уровень внутренней связности последовательности. Уровень боковых лепестков АКФ системы (1) существенно не изменяется при изменении глубин модуляции M и не превышает 0,26. В системе (2) при увеличении глубины модуляции происходит увеличение числа последовательностей с меньшими по отношению к последовательностям, полученным от систем без модуляции, интервалам корреляции (см. рис. 2).

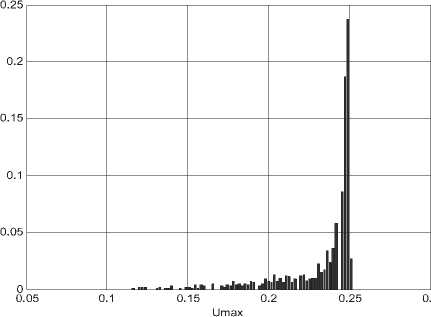
Рис. 2. Гистограммы распределения последовательностей на основе (2) в зависимости от модуля максимального уровня боковых лепестков АКФ M = 0,05

Из рис. 2 видно, что при увеличении M до 0,05 доля последовательностей с уровнем боковых лепестков 0,23…0,26 уменьшается более чем на 10%. В системе Лоренца максимальный уровень боковых лепестков равен 0,18; наиболее вероятные значения уровня боковых лепестков АКФ 0,12…0,13. В системе Чуа максимальный уровень боковых лепестков равен 0,22 с наиболее вероятными значениями 0,12…0,14. Уровень боковых лепестков АКФ систем Лоренца и Чуа в условиях квазирезонансных воздействий на параметр временной дискретизации в два раза выше, чем у М -последовательностей. Для систем (1)-(2) этот уровень выше в четыре раза.

Взаимокорреляционные функции двоичных псевдослучайных последовательностей имеют особенно важное значение для систем связи на основе прямого метода расширения спектра. При этом основным параметром, оцениваемым по взаимокорре-ляционной функции, является максимальный уровень бокового лепестка. Уровень боковых лепестков важен при выборе порога устройств приема систем с кодовым разделением каналов. Проведенный анализ показал, что максимальный уровень боковых лепестков взаимокорреляционых функций не превышает 0,28 для системы (1) и 0,26 для системы (2). Этот уровень практически не изменяется при модуляции параметров временной дискретизации систем, так же как и для систем Лоренца и Чуа [6]. В целом, уровень боковых лепестков ВКФ для всех четырех исследованных систем сопоставим с М -последо-вательностями. Системы Лоренца и Чуа обладают преимуществом в меньших значениях интервалов корреляции формируемых двоичных последовательностей и большей гибкостью управления этими интервалами в сравнении с системами ДК и АА.

Выводы

Квазирезонансные воздействия на параметры временной дискретизации нелинейных систем ДК и АА с динамическим хаосом являются эффективным средством управления корреляционными характеристиками двоичных псевдослучайных сигналов, сформированных на их основе. Применение ква-зирезонансных воздействий на параметры временной дискретизации сигналов систем ДК и АА позволяет управлять интервалами корреляции двоичных псевдослучайных последовательностей, сформированных на основе этих систем, и сократить интервалы корреляции двоичных последовательностей в два раза по сравнению с сигналами систем без управляющих воздействий. Изменение глубины модуляции параметров временной дискретизации в системах ДК и АА не приводит к значимым изменениям в уровнях взаимной корреляции двоичных последовательностей, сформированных на их основе.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (проект РФФИ №10-08-00178-а) и ОАО «НПО «Радиоэлектроника» им. В.И. Шимко».