Статистические характеристики информационных потоков прибытия составов поездов на станцию Челябинск-Главный

Введение ¹

Одной из актуальных задач, стоящих перед Южно-Уральской железной дорогой является сокращение непроизводительных потерь на сортировочных станциях. Южно-Уральская железная дорога – филиал ОАО «РЖД» сегодня обеспечивает перевозку грузов как внутри, так и вне Российской Федерации (Республика Казахстан). К перевозочному процессу возрастают требования по обеспечению качественной услугой клиентов компании [1]. Движение информационных сообщений между системами обладает в некоторых случаях большой инерционностью, и некорректный ввод информации сотрудниками в систему приводит к значительным искажениям результатов прогнозирования.

Точное время прибытия поезда на станцию определяет дежурный по станции с соответствующим вводом (регистрации) информации в Гид «Урал-ВНИИЖТ». При этом существенную роль играет человеческий фактор в прогнозировании времени прибытия. Это влияет на качество прогноза работы станции, так как из-за отклонений информация становится недостоверной и теряет свою актуальность. Чем шире интервал прогнозирования, тем больше отклонения.2

При использовании статистического анализа для составления прогноза оперативные работники станции получают данные, составляющие существенную компоненту системы поддержки принятия стратегических решений, что позволит прогнозировать работу сортировочной станции в заданном доверительном интервале [2].

Статистический анализ

Для статистической обработки информационных потоков поступающих составов поездов выбраны данные о поступивших поездах на станцию Челябинск-Главный за 7 суток. Выборка произведена на станции Челябинск-Главный с помощью существующей автоматизированной системы АСУСТ. Данные о времени прибытия содержат два времени прибытия составов поездов на станцию: первое время – время, которое введено в Гид «Урал-ВНИИЖТ» дежурным по станции – зарегистрированное время, и второе время – фактическое время прибытия состава на станцию.

На рис. 1 представлена гистограмма соотношения частоты от интервалов разности во времени прибытия составов на станцию.

• 1.    Математическое ожидание

• 2.    Дисперсия

• 3.    Среднеквадратическое отклонение составляет

y 4si _x

M(x) = ^ = 6,75 минут на состав.(1)

5 4 ^s1 М[|Х-М(х)| ²]

D(X) = —-----------1 = 55,77 (минут) на состав.(2)

• 6    = ^D (х) = 7,47 минут на состав.(3)

Эти величины характеризуют отклонение времени в поступлении составов поездов, зарегистрированного дежурным по станции в Гид «Урал-ВНИИЖТ», и фактического, зарегистрированного в АСУ СТ. Отклонения влияют на достоверность составления прогноза поездообразования внеклассной сортировочной станции Челябинск-Главный. В статье приводятся средние показатели времени, взятые за 7 суток в период с 1 по 8 ноября 2011 г. Все данные содержатся в анализе работы сортировочной станции в период с 1 по 10 ноября 2011 г.

Следовательно, необходимо осуществлять прогноз поездообразования с применением статистических методов.

Вероятность разности между зарегистрированным и фактическим временем прибытия состава поезда в интервале [0; 10] мин по распределению Пуассона равна сумме вероятностей соответствующих значений либо площади фигуры, расположенной в данном интервале:

Р [0,10]= П=о ^ = 0,98. (5)

Вероятность разности между зарегистрированным и фактическим временем прибытия состава поезда в интервале [0; 10] мин по экспериментальным данным

Р [0,10]= Е П=о ^ п = 0,75, (6) где P _n - вероятность прибытия состава поезда в интервале разности времени n по экспериментальным данным.

Из анализа гистограммы на рис. 1 следует, что разница между зарегистрированным и фактическим временем поступления поездов на станцию Челябинск-Главный характеризуется распределением Пуассона (рис. 2).

Расхождение теоретических и экспериментальных вероятностей прибытия состава поезда в доверительном интервале [0; 10] мин связано с тем, что распределение Пуассона «содержится» в более узких рамках по времени обработки состава, а экспериментальные данные распределены по всем значениям.

Проверим предположение о распределении Пуассона в доверительном интервале с соответствующей вероятностью с помощью теоремы Пирсона.

Для статистического анализа информационных потоков прибытия составов поездов на станцию Челябинск-Главный интервалы разности между зарегистрированным и фактическим временем

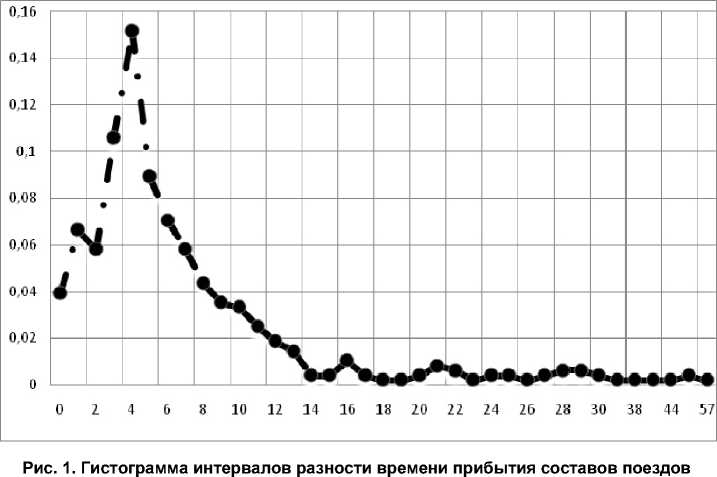
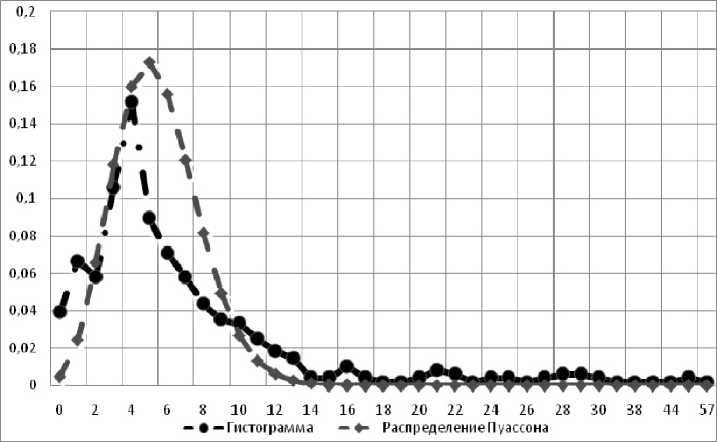
Рис. 2. Гистограмма плотности распределения

Таблица 1

i	0	1	2	3	4	5	6	7	8	9	10	11	12
n i	19	32	28	51	73	43	34	28	21	17	16	12	9
i	13	14	15	16	17	18	19	20	21	22	23	24
n i	7	2	2	5	2	1	1	2	4	3	1	2
i	25	26	27	28	29	30	31–33	34–38	39–40	41–44	45–54	55–57
n i	2	1	2	3	3	2	1	1	1	1	2	1

Таблица 2

i 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 ni 19 32 28 51 73 43 34 28 21 17 16 12 9 9 9 8 8 6 6 6 прибытия поездов на сортировочную станцию разбили на 38 промежутков времени, в каждом из которых регистрировалась разность зарегистрированного и фактического времени прибытия состава поездов на станцию.

Результаты приведены в табл. 1, где наблюдаемые частоты n_i – число промежутков из 38 интервалов, в которых было зарегистрировано соответствующее число i ( i = 0,1, …, 57) составов поездов, прибывших на станцию, с разницей между зарегистрированным и фактическим временем прибытия n i .

На уровне значимости α = 0,05 необходимо проверить гипотезу о том, что случайная величина Х – число прибывших составов поездов на сортировочную станцию во временной промежуток длительностью Δτ – разность между зарегистрированным и фактическим прибытием составов поездов на станцию – подчиняется распределению Пуассона:

I

Р(Х = 1) = _Р1 = ^е~ ^а , (7) где i = 0, 1, …, 57.

Поскольку значение n_i в некоторых столбцах исходной таблицы меньше 5, то объединим их с предыдущими столбцами и получим табл. 2 для расчетов.

Число интервалов i при разбиении отрезка обычно определяют по формуле Старджесса [3]:

i = 1 + 3,32 lnn, (8) где n – число составов поездов, прибывших на станцию в среднем за сутки в период с 01.11.2011 г. по 08.11.2011 г.: i ~ 22 интервала, что практиче- ски совпадает с количеством интервалов на практике (в результате преобразований получено 20 интервалов времени).

Используя данные таблицы, вычислим значение Т оценки неизвестного параметра а распределения Пуассона (Т = х, где х - выборочное среднее):

х = ^⁹₀гп₁, (9) где и - число составов поездов, прибывших на станцию в среднем за сутки в период с 01.11.2011 г.

по 08.11.2011 г. (и = 436). 2694

х =    = 6,18 = т.

436               ^е

Заменим в гипотетическом распределении а ‘

Пуассона P i = —е ^a неизвестный параметр с значением его оценки Т , вычисленным по экспериментальной выборке, Т = 6,18.

Таким образом, проверке подлежит гипотеза Н_о :

р ^ -р Ое -^ ^-^                    (11)

против альтернативы Н₁: р ^ ^ р^о _е , i = 0, 1, ..., 19 на уровне значимости α = 0,05. Заметим, что проверяемая гипотеза Н _о - сложная, так как распределе -ние содержит неизвестный параметр a , значение которого заменено значением его оценки се [3].

В табл. 3 приведен расчет величины у2 — У19 (™.—Vie?

^Х е - L i=o 7^5    .                        ⁽¹²⁾

np ie

Заметим, что при расчете «теоретических» вероятностей в случае целочисленного распределения для крайних значений выборки следует крайние интервалы считать полубесконечными. В интервале i > 13 значения и вычисления соответст- венно необходимо отбросить, так как данные интервалы содержат мало случаев. Таким образом, табл. 3 преобразуется в табл. 4 значений, которые стоит учитывать.

В методе хи-квадрат для случая сложной гипотезы статистикой критерия служит Х²_к-1-1 [3], где l – число параметров, оцениваемых по выборке; k – максимальное значение числа i , зарегистрированное в данном эксперименте (аналог числа интервалов разбиения, используемого в методе хи-квадрат при проверке гипотезы о непрерывном распределении); в данном случае k = 37.

Учтем, что 17 последних столбцов исходной таблицы были объединены в несколько, поэтому k* = k – 17 = 20, а также то, что в неизвестное зна-

Таблица 3

i	n i	i n i	р Ое	Пр Ое	(^ 1 - Пр Ое ) 2 ^р Ое
0	19	0	0,002070	0,995876	325,4909
1	32	32	0,012795	6,154512	108,5365
2	28	56	0,039537	19,01744	2,121377
3	51	153	0,081447	39,17593	3,568736
4	73	292	0,125835	60,52682	2,570436
5	43	215	0,155533	74,81115	3,381679
6	34	204	0,160199	77,05548	3,007207
7	28	196	0,141432	68,02898	3,92558
8	21	168	0,109257	52,55239	3,157336
9	17	153	0,075023	36,08597	2,523656
10	17	170	0,046364	22,30113	1,260115
11	12	132	0,026048	12,52918	0,02235
12	9	108	0,013415	6,452528	1,005747
13	9	117	0,006377	3,067433	11,47388
14	9	126	0,002815	1,354052	43,17448
15	8	120	0,001160	0,55787	99,28002
16	8	128	0,000448	0,215477	281,2308
17	6	102	0,000163	0,078332	447,659
18	6	108	0,000056	0,026894	1326,611
19	6	114	0,000018	0,008748	4103,398
	436	2694	1,0	436,0	Х е 2=6773,399

Таблица 4

i	ni	i ni	р Ое	Пр Ое	(^ 1 - ^р 0е ) 2 ^р Ое
2	28	56	0,039537	19,01744	2,121377
3	51	153	0,081447	39,17593	3,568736
4	73	292	0,125835	60,52682	2,570436
5	43	215	0,155533	74,81115	3,381679
6	34	204	0,160199	77,05548	3,007207
7	28	196	0,141432	68,02898	3,92558
8	21	168	0,109257	52,55239	3,157336
9	17	153	0,075023	36,08597	2,523656
10	17	170	0,046364	22,30113	1,260115
11	12	132	0,026048	12,52918	0,02235
12	9	108	0,013415	6,452528	1,005747
	333	1847	1,0	468,5	Х е 2=26,54422

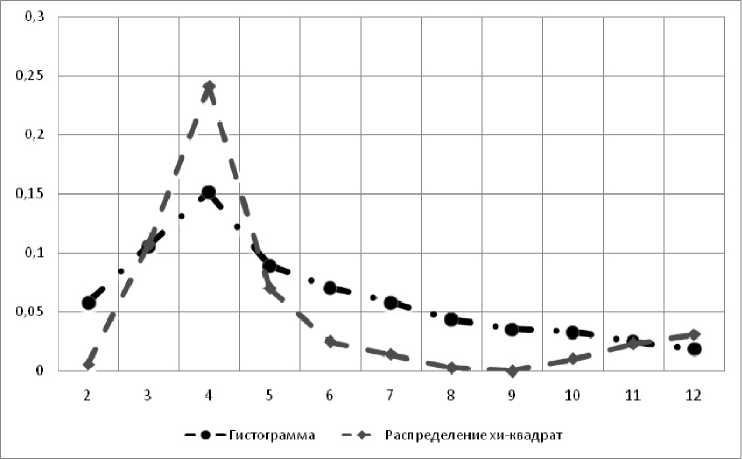
Рис. 3. Гистограмма и функция хи-квадрат в отрезке [2; 12]

чение параметра распределения а было заменено значением его оценки о ^ , поэтому число степеней свободы равно окончательно k* - l - 1 = 19.

Квантиль порядка 0,95 распределения X2 с числом степеней свободы, равным 19,

Х² кр = X² _19:0-95 = 30,14 3 5. (13)

Поскольку А² _е = 26,54422 < 30,1435 = Х²_кр, нет оснований для отклонения гипотезы Н₀.

Таким образом, гипотеза Н ₀ о том, что случайная величина - количество составов поездов, прибывших на сортировочную станцию Челя-бинск-Главный с разницей зарегистрированного и фактического времени прибытия на станцию за промежуток времени Ат, подчиняется распределению Пуассона с параметром, равным а ^ = 6,18, не противоречит результатам наблюдений и может быть принята на уровне значимости а = 0,05 на отрезке [2; 12].

На рис. 3 представлены гистограмма и функция хи-квадрат на отрезке разности между зарегистрированным и фактическим временем прибытия [2; 12] мин.

В результате аппроксимации и проверке гипотезы о распределении Пуассона разности во времени прибытия составов поездов на станцию между зарегистрированным и фактическим установлено, что подчиняется распределению Пуассона с параметром, равным а^ = 6,18, не противоречит результатам наблюдений и может быть использовано с доверительной вероятностью 0,95 на отрезке [2; 12]. Следовательно, при регистрации сообщения о прибытии поезда на станцию дежурным по станции в Гид «Урал-ВНИИЖТ», разность между прогнозируемым и фактическим временем прибытия составов поездов на станцию будет в пределах [2; 12] мин в 95 % случаев.

Заключение

Использование статистического анализа в качестве вспомогательного инструмента для составления прогноза поездообразования на сортировочной станции Челябинск-Главный и в принятии решений позволит повысить достоверность прогноза в заданном интервале времени путем минимизации влияния человеческого фактора. Разность между зарегистрированным и фактическим временем прибытия состава поезда характеризуется законом Пуассона в пределах отрезка [2; 12] мин с доверительной вероятностью 0,95.