Статистические характеристики поля апертурной случайной антенны

Типовые варианты реализации апертурных СА относятся к подклассу антенн со случайной конфигурацией и случайными характеристиками возбуждения, куда входят как одиночные СА, так и антенные решетки со случайным числом и расположением элементов [1-2]. Практическая значимость анализа и моделирования параметров таких СА обусловлена тем, что источники электромагнитного излучения (ЭМИ), связанные с формированием каналов утечки конфиденциальной информации (КИ) – апертурные утечки КИ [3], можно рассматривать как апертурные СА. Примерами апертурных СА являются дефекты герметичных по ЭМИ конструкций (щели, зазоры, поврежденные швы и стыки в экранирующих корпусах и камерах), технологические отверстия, двери и окна в помещениях, подлежащих защите (ПЗП), оборудованных для ведения переговоров, обмена и обработки КИ. С точки зрения статистической теории антенн (СТА) представляют интерес две проблемы: исследование процессов возбуждения апертурных СА исходными КИ-сиг-налами (имеющими в ряде случаев отличную от ЭМИ физическую природу) и анализ структуры ЭМИ, создаваемых ими во внешней среде, – кото- рые связаны, соответственно, с внутренней [4-5] и внешней [6-8] задачами электродинамики.

В [2; 4-5; 7-9] показано, что эффективным средством решения указанных задач является метод СИМ, использующий метод Монте-Карло. Возможности СИМ позволяют воспроизводить и анализировать структуру ЭМИ на разных расстояниях от СА и при разных вероятностных моделях случайных отклонений от заданных детерминированных значений пространственных координат, амплитуд, фаз и временных сдвигов сигналов, возбуждающих элементы СА (геометрических, амплитудных, фазовых и временных ошибок), что является традиционным содержанием СТА. Из новых задач можно отметить исследование стохастических поляризационных эффектов в СА разной конструкции; анализ и моделирование энергетического потенциала конкретных СА; построение вероятностных моделей сигналов, создаваемых СА, с целью сопоставления их с законами Релея, Райса и другими известными распределениями, а также с моделями, полученными в условиях применимости обобщенной центральной предельной теоремы теории вероятностей на основе семейства одномерных устойчивых законов [10-11].

Цель статьи – описание предметной области и определение исходных данных для проведения СИМ в рамках построения вербальной модели апертурной СА, а также анализ результатов СИМ применительно к возбуждаемой случайным КИ-сигналом СА, состоящей из трех прямоугольных апертур, которая моделирует поверхность стены ПЗП с окнами, ориентированными в направлении возможного перехвата КИ.

Вербальная и математическая модели СА. Исходные данные для проведения СИМ

Геометрию решаемой задач иллюстрирует рис. 1. Трехэлементная апертурная СА расположена на поверхности S_A , совпадающей с внешней стеной ПЗП и плоскостью X0Y прямоугольной системы глобальных координат; размеры одной прямоугольной апертуры Ixh, расстояние между соседними апертурами (шаг решетки вдоль оси y ) равняется d ; расстояние от S_A до плоскости S_М , в которой определяется структура ЭМИ, равно R_A ; расстояние от элемента СА, расположенного в точке М_А на поверхности S_A , до точки наблюдения М_S на плоскости S_М есть r_A .

Будем считать, во-первых, что источник КИ-сигнала, расположенный слева от S_A в глубине ПЗП, создает на раскрыве СА сложное по структуре (неравномерное, несинфазное, стохастическое и т.п.) возбуждающее поле E_o с круговой частотой CO к, соответствующей k -ой гармонике его частотного спектра. Во-вторых, что возбуждающее СА поле можно представить в виде суперпозиции регулярной (квазидетерминированной) и нерегулярной (случайной) составляющих, как это принято в СТА. На регулярное поле, равномерное (или квазиравномерное) в пространстве по амплитуде и фазе, накладывается нерегулярная составляющая в виде совокупности амплитудных и фазовых случайных «ошибок» (далее без кавычек), представляющих собой случайные отклонения от равномерных распределений амплитуд и фаз.

В-третьих, если расположение и режим работы источника КИ, влияние конфигурации и инфраструктуры ПЗП, а также другие случайные факторы, воздействующие на СА, при постановке и решении внутренней задачи приемлемым (достаточно определенным и достоверным) образом описать не удается, взаимно независимые (или коррелированные) значения ошибок в рамках метода СИМ допустимо «разыгрывать» с помощью метода Монте-Карло для заданного априори вероятностного закона (равномерного, нормального, устойчивого и т.п.). При этом отметим, что возможности СИМ позволяют достаточно просто оценивать степень робастности вариантов решения внешней задачи и исследовать влияние кумулятивности исходных данных на точность и достоверность получаемых результатов – что представляется одним из важных достоинств данного метода [2; 4-5; 7-8]. Исходные данные для проведения СИМ могут быть конкретизированы и уточнены экспериментальным путем на моделях и в реальных ПЗП, а в тестовых случаях – при помощи упрощенных расчетных соотношений.

При переходе от вербальной к математической модели апертурной СА будем считать, что элемент СА, расположенный в точке М_А , представляет собой излучатель Гюйгенса dS = dx-dy, в котором виртуальный электрический ток 1_Э = E_o dx! Z_Q ; магнитный ток 41 — Eq dy, и для гармонического режима работы излучателя комплексная амплитуда его напряженности поля в локальной системе совмещенных прямоугольных x ; y ; z и сферических r ; 9; ф координат (см. рис. 2) представляет собой [8]

_    Eodxdy .    /        x_ dEe = —-------sin ф (I + cos 9) e, dE = ^ ^X^ cos ф (1 + cos 61) e~'"'',(1)

^TA где A = 2л Vo !o) k – длина волны, соответствующая гармонике CO k"i Eo И Zq — соответственно, волновое сопротивление и скорость света в окружающей среде; x; y; z – прямоугольные глобальные координаты точки МА на плоскости SA ; xm; ym; zm – прямоугольные глобальные координаты точки МS на плоскости SM ; другие обозначения соответствуют рис. 1-2.

Отметим, что в (1) учтено предполагаемое равенство значений волнового сопротивления среды в апертуре СА и внешнем пространстве, а также что расстояние 4 =>i5I-xf+U4^yf4z^ здесь соответствует условию krA >> 1 для дальней (волновой) зоны Фраунгофера, где k = 2л IX – волновое число, а размеры каждого излучателя Ex ® dx и Ay ~ dy должны соответствовать kEx « 1; kEy « 1, и это необходимо будет учитывать при разбиении апертуры СА на элементы с учетом текущих значений rA и X.

Выполним преобразование локальных сферических и прямоугольных координат

.             у                       X sin ф =         ^ ; COS ф = .       =

Vx2+y2        yx-^y- и преобра зование при переходе от локальных прямоугольных координат к глобальным координатам:

sin^p = Ут V ;

X^хrn --v)² +(z„ -y)²

COS ф =

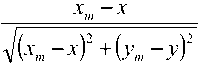
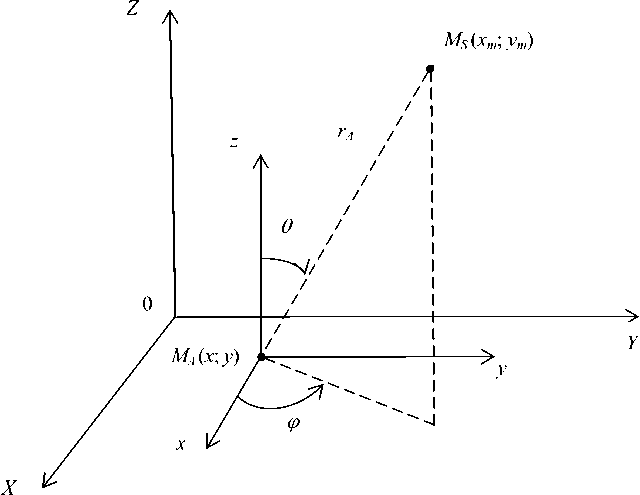
Рис. 2. Расположение излучателя Гюйгенса dS = dx-dy в точке М_А(х\ у) на плоскости S_A в совмещенной системе прямоугольных и сферических глобальных и локальных координат

cos 9 =——

*'а после чего получим (1) как

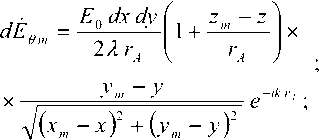
y ). Ориентацию указанных составляющих вектора E в точке наблюдения M_S ( x_m ; y_m ) для излучателя, размещенного в центре координат, иллюстрирует рис. 3 – где ортогональные составляющие в прямоугольных координатах условно показаны в точке M_A .

dE,

Eo dx dy

IX rA

zm — z

ГА

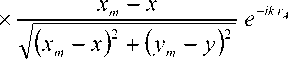
Представим (2) в тригонометрической форме

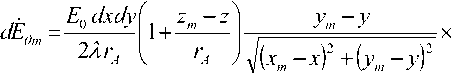
х [cos(^r () - / sin(h; ()];

dE„m

E_odxdy ( ! z_m -z

x [cos(^r₄) - i si n(A/;_l)]

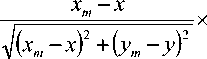
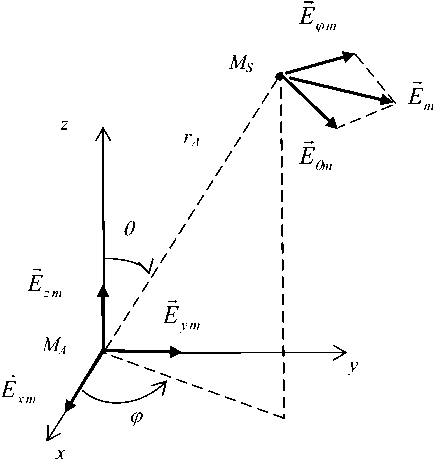
Рис. 3. Пространственная ориентация составляющих вектора E_m

и разложим составляющие и по базису глобальной системы прямоугольных координат, чтобы рассчитать суперпозицию полей от совокупности произвольно расположенных излучателей M_A ( x ;

Правильность последующих преобразований контролируется по двум условиям: во-первых, ортогональные составляющие E' _m в точке наблюдения для глобальной и локаль-

ной систем прямоугольных координат должны быть равны между собой, так как орты у этих систем параллельны друг другу; во-вторых, модуль вектора Е должен быть одинаковым в любой системе координат. Поскольку dE9m = (х0 cos^> cos5 + у0 sin#? cos5-

• - z₀ sin0^,„;

dE^ = (-x0 sin ф + y0 cos^2) dE^, (4) получаем в комплексной форме dExm = dЁ9m cosy cos0 - dE^ sin^;

dE_ym = dЁ_вm &тф cos 5 + dE^ cosp; (5)

dEzm = —dE9m sin 5, и в итоге dE xm = dEm0 (cos 0 - 1) sin ф cos ф x . x [cos (kr 4) - z sin (kr4)];

dE_ym = dE_m0 (sin² ф cos 0 + cos² ф^ x . ₍₆₎ x [cos (At^ ) - z sin ^kr_A)];

dE,_m = -dE_nM sin ф sin 0 [cos (Ar,) - г sin (kr_A)]

EMxdv_ где dEm0 =------— (l + cos5). Модуль ком- комплексной амплитуды вектора, соответствующего правой части (6), равняется dEm0, поэтому второе условие здесь выполняется. Выделив в (6) действительные и мнимые части, можно интегрировать их по апертуре СА путем численного суммирования, поскольку орты Х(рУ(Мо у глобальной и локальной систем прямоугольных координат одинаковы и не меняют свою ориентацию при перемещении точки наблюдения Ms в окружающем пространстве – то есть первое условие при этом выполняется автоматически.

Результатом интегрирования (6) по всем трем прямоугольным апертурам, входящим в состав СА (см. рис. 1), являются действительные и мнимые части составляющих напряженности поля f; E_v; E_ . Модуль напряженности поля при этом есть

\Ё I = [(Re Ё ) + (imE Y + (Re Ё ) +

'        /        / <7)

+ (lm£v )2 + (Re£, )2 + (imE. )2 ]1/2.

Метод моделирования коррелированных ошибок в апертуре СА

Амплитудные и фазовые ошибки вводятся в (5)-(6) принятым в СТА и оговоренным выше способом:

Ё_т0 = Е₀(1 + а_Е)ехр(-]ф_ЕЕ (8)

где aE = ML / Eo; ML – амплитудная ошибка; Фе – фазовая ошибка. Тогда (6) в прежних обозначениях будет иметь вид dExm = dEm0 (1 + aE )(cos 5-1) sin ф cos ф x x [cos (h-4 + фЕ)- z sin ^krA + фЕ)];

dE_ym = dE_m0 (\ + a_E )(sin² ф cos5 + cos² ф^ x ^ x [cos(Az'₄ + ф_Е ) - z sin (kr_A + ф_Е)];

dE.m = -dEm0 (1 + aE ) sin ф sin 0 x x [cos (krA +фЕ)-1 sin (krA + фЕ )].

Значения ошибок ^aE ^и Фе ’ которые фигурируют в (9), в рамках метода СИМ необходимо «разыгрывать» методом Монте-Карло для заданных законов распределения этих ошибок [4-5] и с учетом их возможной корреляционной зависимости друг от друга. Схема моделирования при этом такова: амплитудные a_F и фазовые Фе ошибки можно считать взаимно независимыми [7], однако их собственными пространственными связями пренебрегать нельзя. В то же время разыгрывать независимые значения ошибок, а затем производить их преобразование в последовательности коррелированных ошибок по аналогии с [9] тоже нельзя – поскольку в данном случае матрица преобразования, с учетом множества элементов Гюйгенса, используемых в расчетах, оказывается неприемлемо большой.

Поэтому вместо общепринятых в СТА моделей коэффициента пространственной корреляции вида R,„„ =exp[-(r„ -F,J2/E2] и Rnm ^exp(-|r„ -rm\/R0\ где ^0 – радиус корреляции ошибок для элементов СА с координатами rn и rm , было предложено ввести эффективный кластерный коэффициент корреляции Rg , который способен принимать два дискретных значения: R3 = 1 в пределах каждого кластера в апертуре СА и ^3 = 0 за пределами данного кластера. Другими словами, значения однотипных ошибок предполагаются постоянными: aE = const и ^P E = const в пределах каждого кластера, а от кластера к кластеру изменяются случайным и независимым друг от друга образом. Поскольку в данном случае геометрические размеры (определяющие площадь) прямоугольного кластера выполняют роль радиуса пространственной корреляции R 0 9 усилению связи между однотипными ошибками (росту r о) соответствует уменьшение числа кластеров NK в составе апертурной СА, а ослаблению корреляционной связи (уменьшению 7?0), напротив – увеличение числа кластеров NK.

Предложенная модель ориентирована специально на исследование апертурной СА с применением метода СИМ и в какой-либо дополнительной адаптации – в отличие, например, от [9], не нуждается. При тестировании СИМ-модели можно исходить из того, во-первых, что в обоих предельных случаях: при N_K. = 1 (что эквивалентно R о >>  L_m , где L_m – максимальный линейный размер СА) и при N_K. >> 1 (что эквивалентно L_m >> 7? 0 ) влияние ошибок на уровни напряженности поля СА является минимальным, поэтому распределения E(S_M) или E4S_M) наплоскости _М (см. рис. 1) при наличии и отсутствии ошибок будут отличаться друг от друга на величину погрешности проводимого компьютерного (численного и имитационного) эксперимента. Во-вторых, что между предельными значениями N_K. = 1 и N_K. >> 1 должен быть (или может быть) вариант, соответствующий максимальному влиянию коррелированных ошибок Q _E и Фе на функцию указанных распределений напряженности поля СА.

Для проверки обоих утверждений методом СИМ были исследованы реализации распределения ^E4s_M^ для семи моделей пространственной корреляционной связи между ошибками в трехэлементной апертурной СА:

• 1)    при отсутствии кластеров, когда в СА все QE COnSt и ф_Е = const, то есть ошибки на форму E\S_M) не влияют;

• 2)    при N_K. = 1, когда в пределах каждой из трех апертур в составе СА (см. рис. 1) значения a_E = const и ф_Е = const, но при переходе от апертуры к апертуре ошибки изменяются независимым друг от друга образом;

• 3)    при N_K. = 4, когда в пределах 1/4 площади каждой из трех апертур в составе СА значения a_E = const и ф_Е = const, но при переходе от одной части апертуры к другой и от апертуры к апертуре ошибки изменяются случайным и независимым друг от друга образом;

• 4)    при N_K. = 16, когда вышесказанное относится к 1/16 площади каждой из трех апертур в составе СА;

• 5)    при N_K. = 64, когда вышесказанное относится к 1/64 площади каждой из трех апертур в составе СА;

• 6)    при N_K. = 256, когда вышесказанное относится к 1/256 площади каждой из трех апертур в составе СА;

• 7)    при N_K. = N_Г. , где N_Г. >> 1 – число элементов Гюйгенса в составе СА.

По результатам СИМ был сделан вывод о том, что наихудшим случаем, с точки зрения влияния на неискаженную ошибками функцию E\S_MV является вариант N_K. = 1 – отсюда следует, что разыгрывать независимые ошибки с помощью метода Монте-Карло [4-5] достаточно лишь при переходе от одной апертуры в составе трехэлементной СА к другой. Отметим также, что предлагаемый способ учета влияния корреляционных связей между ошибками в апертуре является достаточно гибким и универсальным в том смысле, что позволяет исследовать свойства СА вне зависимости от режима ее работы (гармонический, шумовой, импульсный и т.д. [7]).

Комплексное тестирование программы расчета характеристик апертурной СА

Тестирование проводилось в четыре этапа: на первом этапе качественно проверялись косвенные признаки правильности работы детерминированной части программы: по характеру пространственно-углового распределения (динамика уровней, симметричность относительно оси Z на рис. 1 и т.п.) действительных и мнимых частей составляющих E_x; E_v и E_ в пределах плоскости S_М с размерами 20×20 м² для трехэлементной решетки синфазно возбужденных апертурных СА (подробнее см. далее) в отсутствие амплитудных и фазовых ошибок. На втором этапе рассчитанные уровни ^Ex^ ^Ey ^{И E}z в волновой зоне Фраунгофера для уединенной прямоугольной апертуры на расстояниях R>2L4A, где L – максимальный размер апертуры; λ – длина волны, сопоставлялись с аналитическим результатом ^Eo для прямоугольной синфазной излучающей поверхности [6].

Критерием количественной оценки при этом была относительная погрешность 5_e =(|Ё|- E_nME_n, где ^ соответствует (7) с учетом ^E v » ^Ez и ^Ex = 0. На третьем этапе, по аналогии с [4-5], контролировались процедуры «разыгрывания» методом Монте-Карло слу-

Таблица 1. Результаты тестирования программы определения Re( E_v._ ); Im( E_v._) на частоте 1 МГц

Точка на SM	-10	-5	0	5	10
МЁ0	6,20839-10"4	6,96274-10"4	7,24619-10"5	6,96274-Ю"4	6,20839-10"4
Im( Ёу )	-4,84577-10"4	-5,16098-10"4	-5,27626-10"4	-5,16098-Ю"4	-4,84577-Ю"4
Ке(Ё:)	2,0519-10"4	1,14995-Ю"4	-1,86194-Ю"19	-1,14995-Ю"4	-2,0519-10"4
Im( Ё.)	-1,6077-10"4	-8,55825-10"5	—1,35104-Ю'19	8,55825-Ю"5	1,6077-Ю"4

Таблица 2. Результаты тестирования программы определения Re( E_v. _); Im ( E_v., ) на частоте 100 МГц

Точка на SM	-10	-5	0	5	10
МЁ0	-3,706-10"2	4,258-Ю"2	8,880-Ю"2	4,258-10"2	-3,706-Ю"2
ШЁ^	8,497-Ю"3	-5,888-Ю"2	-9,673-10"3	-5,888-Ю"2	8,497-10"3
МЁЛ	-1,Ю0Ю"2	4,853-10"3	1,004-10"14	-4,853-Ю"3	1,100-Ю"2
1т(£.)	5,959-Ю"3	-1,105-Ю"2	-3,188-Ю"15	1,105-Ю"2	—5,959-Ю"3

Таблица 3. Результаты тестирования программы определения Re( Ё _); Im ( Е_у. _) на частоте 0,5 ГГц

Точка на SM	-10	-5	0	5	10
МЁ0	-4,65857-10"3	-8,81731-10"2	0,352541	-8,81731-Ю"2	-4,65857-Ю"3
Im( Ёу )	0,101535	-9,25303-10"2	-0,210944	-9,25303-10"2	0,101535
Re(K)	2,34612-10"3	-1,78865-Ю"2	-6,61333-Ю"18	1,78865-Ю"2	-2,34612-10"3
Im( Ё,)	2,97967-10"2	-9,30067-Ю"3	1,11519-Ю"16	9,30067-Ю"3	-2,97967-10"2

Таблица 4. Результаты тестирования программы определения Rel E^ _); Im(£'v.T) на частоте 1 ГГц

Точка на SM	-10	-5	0	5	10
^(Ёу)	0,104	-0,233	0,309	-0,233	0,104
1т( Ёу)	-1,601-10"2	-5,442-Ю"2	-0,539	-5,442-Ю"2	-1,601-Ю"2
Re(£.)	3,063-Ю"2	-2,606-Ю"2	-1,ЗО5-Ю"13	2,606-Ю"2	-3,063-10"2
1т( Ё.)	-5,459-10"3	-7,015-Ю"3	-2,665-10"14	7,015-10"3	5,459-10"3

чайных значений ^ е ^ Фе ’ фигурирующих в (9), для заданных законов распределения этих ошибок и с учетом их корреляционной зависимости (или независимости) друг от друга. На четвертом этапе определялись уровни Ех; Е у и Е-_ при полностью коррелированных ошибках (для NK = 1) и при отсутствии ошибок а Е; фЕ в рассматриваемой трехэлементной СА – в соответствии с высказанным предложением использовать меру различия между ними для оценки погрешности проводимого компьютерного (численного и имитационного) эксперимента.

Результат тестирования иллюстрирует таблицы 1-3, где в качестве примера представлены значения ^^ЕУ^ и \ш^Е..ф для рассматриваемой трехэлементной апертурной СА на частотах 1 МГц; 10 МГц;

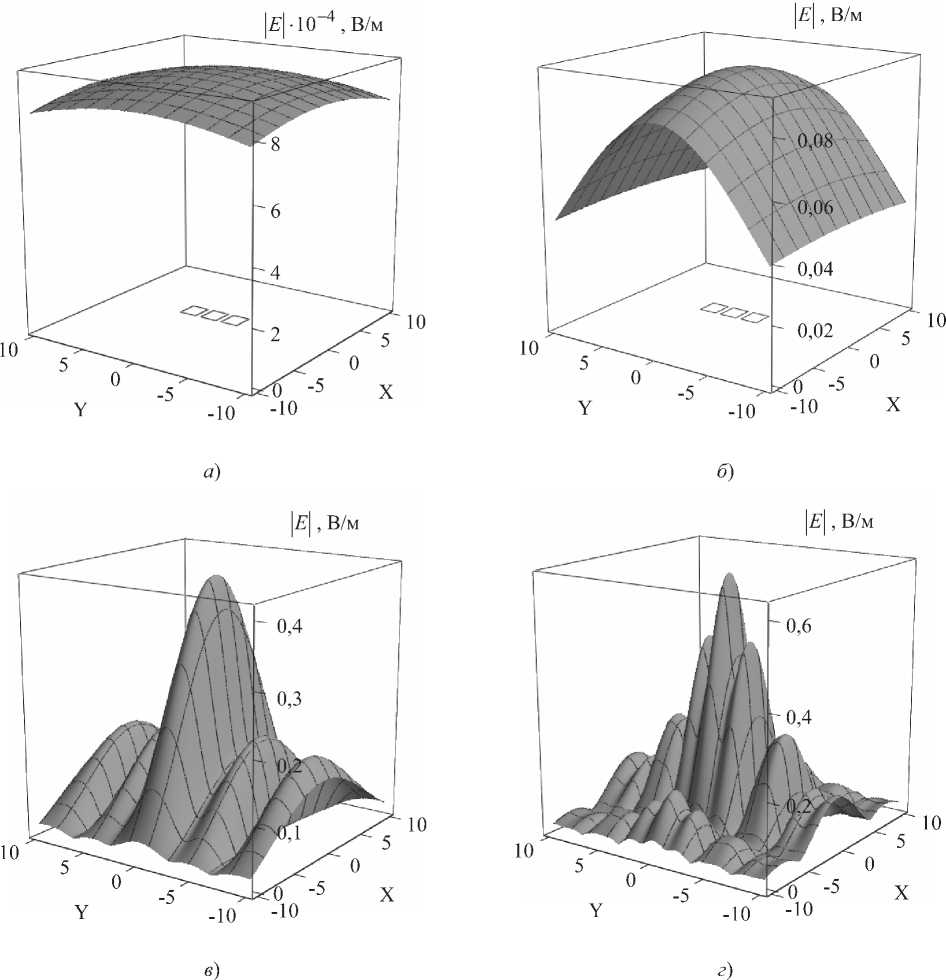
Рис. 4. Распределения модуля £ в пределах плоскости SmC размерами 20x20 м² для трехэлементной решетки апертурных СА при отсутствии амплитудных и фазовых ошибок:

а) частота 1 МГц; б) 100 МГц; в) 0,5 ГГц; г) 1 ГГц.

0,5 ГГц и 1 ГГц соответственно, полученные двумя указанными способами в пяти точках на плоскости S_М с координатами Z = R_А = 30 м; Y = 0; ±5 м; ±10 м (см. рис. 1), которые оказались совпадающими между собой до всех указанных цифр. Приведенные в таблицах 1-3, а также полученные на предыдущих этапах данные позволяют считать итоги тестирования вполне удовлетворительными и приступить к анализу статистических характеристик напряженности поля рассматриваемой апертурной СА.

Статистические характеристики амплитуды и фазы комплексного вектора напряженности поля апертурной СА

На рис. 4 а-в представлены графики распределения модуля 1^1 в пределах плоскости S_М с размерами 20×20 м² для трехэлементной решетки апертурных СА с параметрами l = 1,8 м; h = 1,5 м; d = 0,5 м при R_А = 30 м (здесь и далее обозначения а-в соответствуют частотам 1 МГц; 100 МГц; 0,5

PW

0,3

0,2

0,1

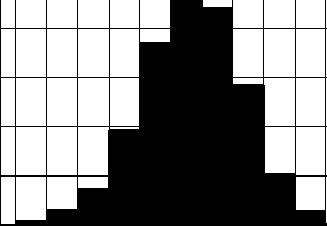
-30   -20   -10    0    10    20

д£, %

а)

Р(М

PW

0,3

О

0,2

0,1

-40   -30   -20   -10    0    10    20

-35   -25   -15   -5     5     15

-70   -50   -30   -10   10    30    50

-60   -40   -20    0    20    40

5Е, %

5Е, %

в)

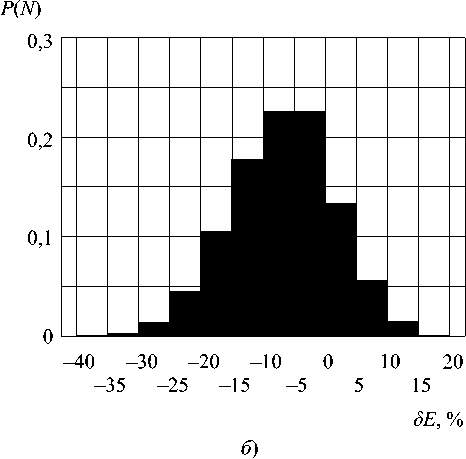
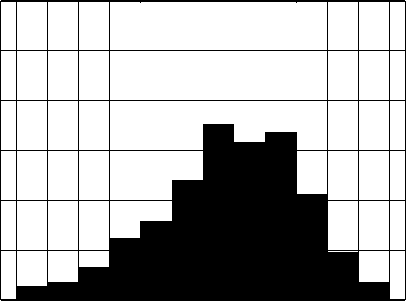
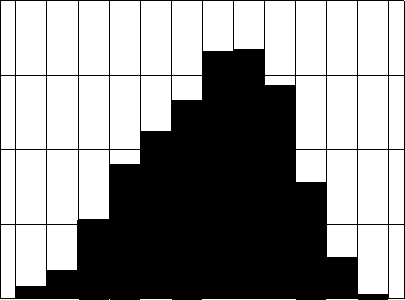
Рис. 5. Гистограммы распределения относительной погрешности 6е, % для модуля S

а) частота 1 МГц; б) 100 МГц; в) 0,5 ГГц; г) 1 ГГц.

ГГц и 1 ГГц) в случае отсутствия амплитудных а_Е и фазовых Фе ошибок.

Данные рис. 4 отражают характер структуры ЭМИ в представляющей интерес с точки зрения защиты КИ достаточно обширной пространственно-частотной области.

Совместное влияние амплитудных аЕ и фазовых Фе ошибок на модуль напряженности поля в точке Z = RА = 30 м; Y = 0 иллюстрируют представленные на рис. 5а-в гистограммы P(dE) = W„/W() относительных случайных отклонений ^ =(|£|-|FJ)/|£J, в процентах, где 1^1 " N – модули комплексных амплитуд напряженности поля (точки сверху опущены), найденные согласно (7) с помощью метода СИМ. Закон распределения ошибок – равномерный в пределах аЕ [–0,2; 0,2] и Фе [–45°; 45°].

Гистограммы на рис. 5 построены для наихудшего с точки зрения искажения формы распределений, показанных на рис. 4, случая N_K = 1, при наличии и отсутствии ошибок соответственно; W_n – число значений |S| ’ попадающих в n -ый интервал на оси абсцисс; W ₀ = 10³ – общее число реализаций |е| . По гистограммам, аналогичным приведенным на рис. 5, могут быть найдены оценки среднего значения, дисперсии, доверительного интервала и др., необходимые для проектирования систем защиты КИ.

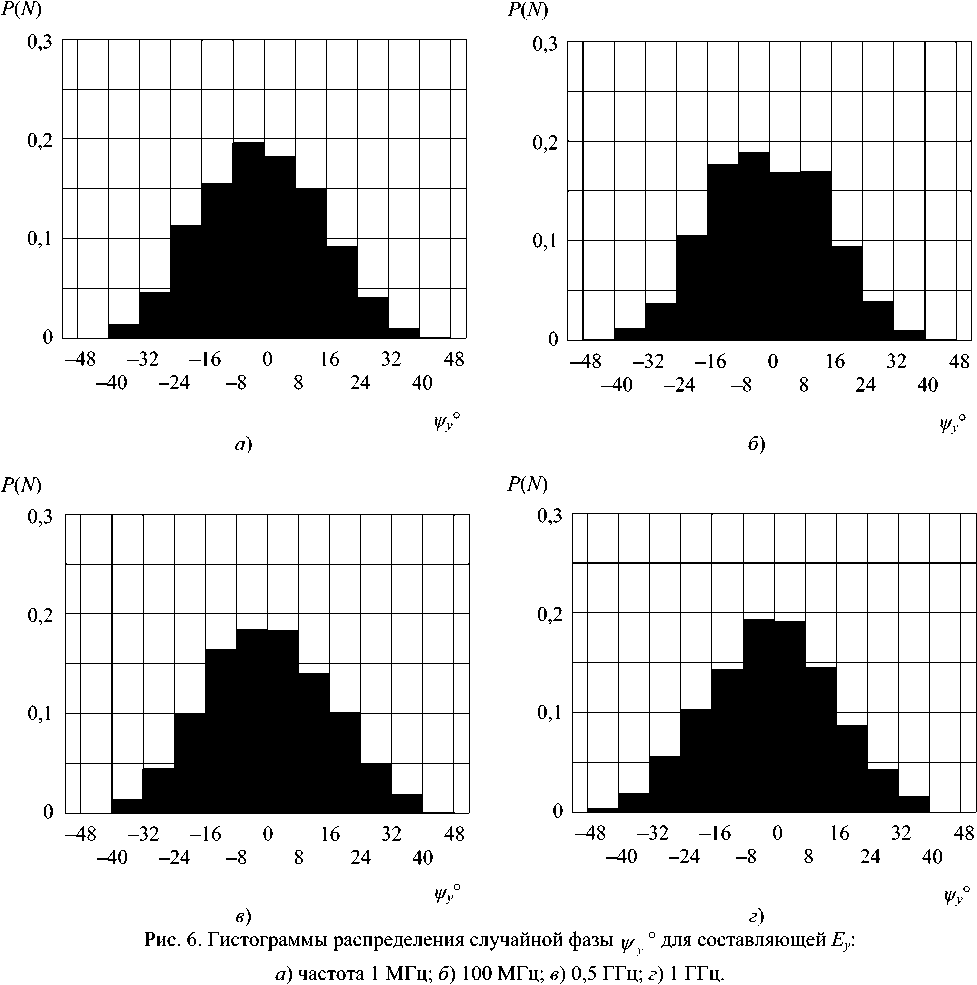
На рис. 6 представлены гистограммы Р(ψ°) значений случайного фазового угла

= arctg

lm(E,)'

i^J

- WyO >

где нижние индексы z относятся к E , приведены на рис. 7. Значения углов Vy^ VzO и их разности на частотах 1 МГц; 100 МГц; 0,5 ГГц и 1 ГГц представлены в таблице 4.

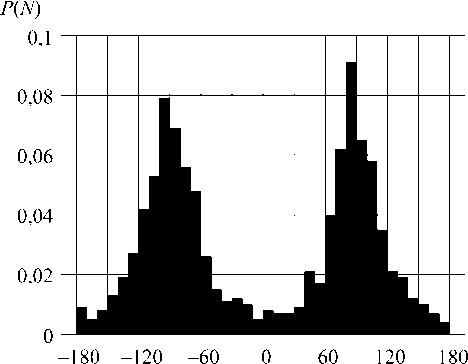
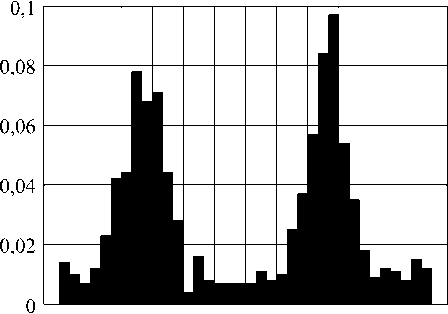
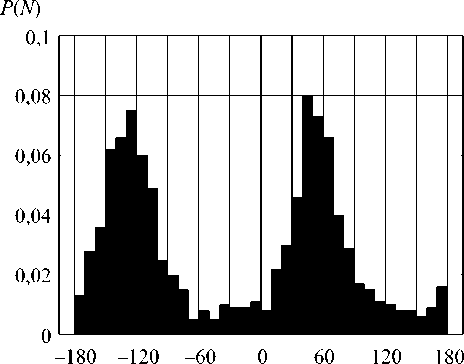
где ^ vO – фаза E_T при отсутствии ошибок, аналогичные приведенным на рис. 5. Гистограммы P(Ey°) случайной разности фаз

ipv -yp = arctg

Im(£v)' КеШ,

- arctg

ImfcJ'

<),

- ^, 0 + VzO

Таблица 4. Фазы составляющих E_v; E. и их разность при отсутствии ошибок

Частота	1 МГц	100 МГц	0,5 ГГц	1 ГГц
^, o °	-36,06°	-6,2°	-30,9°	-60,2°
VzO °	144,04°	161,1°	93,4°	7,4°
VyO-VzO°	-180,1°	-167,3°	-124,3°	-67,6°

PW

-150 -90   -30   30    90   150

-180 -120 -60    0    60   120   180

-150 -90   -30   30    90   150

P(N)

-150 -90   -30   30    90   150

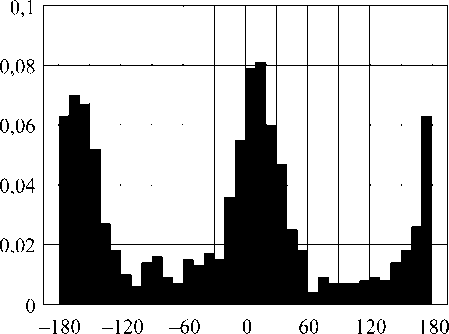
-150 -90   -30   30    90   150

в)

УгУ:?

Рис. 7. Гистограммы распределения случайной разности фаз у/, ° - у/.°: а) частота 1 МГц; 6) 100 МГц; в) 0,5 ГГц; г) 1 ГГц

Данные рис. 7, с учетом результатов расчета амплитуд составляющих Е_х ; Е и Е , позволяют исследовать поляризационные свойства рассматриваемой СА. Поскольку в данном случае E_v » Е, , а Е_х = 0, в центральной точке Z = R_А = 30 м; Y = 0 на частотах до 0,5 ГГц для большинства реализаций |Е| имеет место сто х астическая эллиптическая поляризация вектора Е , где левое и правое направления вращения практически равновероятны, а поляризационный эллипс сильно вытянут и ориентирован вдоль горизонтальной оси Y (см. рис. 1). На частоте 1 ГГц ситуация иная: здесь чаще всего имеет место стохастическая поляризация, близкая к линейной.

При необходимости из гистограмм, аналогичных представленным на рис. 6-7, также может быть извлечена информация относительно числовых характеристик фазовых распределений всех составляющих напряженности поля СА в заданной пространственно-частотной области.

Заключение

Актуальность и значимость исследования СА методом СИМ обусловлены практическим применением этого одного из наиболее перспективных направлений развития СТА в интересах проектирования систем активной защиты КИ [8; 12]. Теоретический интерес представляют возможности СИМ, связанные с исследованием структуры ЭМИ на разных расстояниях от СА и при разных вероятностных моделях амплитудных и фазовых ошибок, что является основным и традиционным содержанием СТА. Кроме того, представленные в настоящей статье результаты анализа и моделирования характеристик апертурной СА в гармоническом режиме целесообразно дополнить аналогичными данными, относящимися к шумовому, импульсному и радиоимпульсному режимам работы СА [7], что также представляет интерес для проектирования перспективных систем защиты КИ.