Статистические методы анализа трафика мультисервисных сетей

Анализ мультисервисного трафика - тема актуальная и распространенная, в особенности в академической среде. Публикации по данной тематике регулярно выходят как в Российской Федерации, так и за рубежом. В отраслевой сфере данной теме уделяется не так мало внимания, что обусловлено, скорее всего, потребительским характером взаимодействия представителей нашей сферы телекоммуникаций по отношению к оборудованию, производимому за рубежом. Тем не менее, в среде ученых тема анализа систем массового обслуживания, потока заявок, трафика компьютерных сетей, вероятностей распределения до сих пор активно обсуждается. Есть ряд не решенных проблемных мест в данной области, и несколько подходов к попыткам их решить. Кто-то рассматривает поток заявок, как процесс самоподобный, кто- то называет его регенеративным, кто-то считает, что трафик можно считать экспоненциальным при больших загрузках и строит свои выводы из этого предположения. Несомненно во всех случаях только одно - поток пакетов в компьютерной сети есть абсолютно случайный процесс, требующий к себе соответствующего отношения.

Когда речь идет об абсолютно случайном процесс мы как правило подразумевает невозможность применения по отношению к нему известных из статистики математических приемов. И в свое время человечество придумало некий псевдослучайные последовательности, которые в той или иной степени в состоянии имитировать случайный процесс. Здесь речь можно вести о так называемых вероятностях распределения. Данный термин подразумевает, что есть некий псевдослучайные последовательности чисел, которые подчиняются заведомо известному закону распределения вероятностей, но данное обстоятельство неочевидно. Определения псевдо случайности возможно только при соблюдении определенных условий.

Если считать, что интервалы времени между приходами пакетов на порт сетевого оборудования есть величины случайные, то возможно имитировать этот процесс применив заведомо известный закон распределения, на основании которого сформировать соответствующую выборку. Мы же предлагаем идти от обратного. Имея на руках выборку временных интервалов между пакетам в сети постараемся определить их принадлежность к какому либо закону распределения. Так как описанные процессы абсолютно случайны и имеют бесконечную энтропию, то однозначного соответствия мы здесь никогда не найдем.

Здесь нам на помощь приходят критерии согласия, смысл которых в проверке неких статистических гипотез. Статистической гипотезой называется любое предположение о законе распределения генеральной совокупности или его параметрах. Обычно гипотезы обозначаются буквой H с индексом. В нашем случае мы будем оценивать статистическую гипотезу, связанную с законом, функцией или плотностью распределения.

Среди критериев согласия выделяют простейший критерий и тест Жарка-Бера. Сразу стоит отметить, что данные критерии производят оценку гипотезу о том, что генеральная совокупность имеет нормальное распределение. Трафик мультисервисной сети есть величина хоть и абсолютно случайная, но тем не менее подчиняющаяся элементарным законом логики. В частности, понятно, что временные интервалы между пакетами не могут быть величиной отрицательной. Нормальное распределений имеет в качестве основных параметров величину первого начального момента и дисперсию. Если дисперсия будет достаточно высока, а математическое ожидание близко к нулю, то возникнет немалая вероятность появления в генеральной совокупности отрицательного распределения. Для случай с моделью реального трафика это неприемлемо. Тем не менее мы провели проверку реального трафика по простейшему методу и по тесту Жарка-Бера, как начальный этап работы. Имея в распоряжении шесть разных фалов данных, различающихся различным условиями получения статистики (разные приборы, протоколы и направления трафика в сети), везде фиксировали одинаковый результат при различных уровнях значимости. А именно непринятие основной гипотезы.

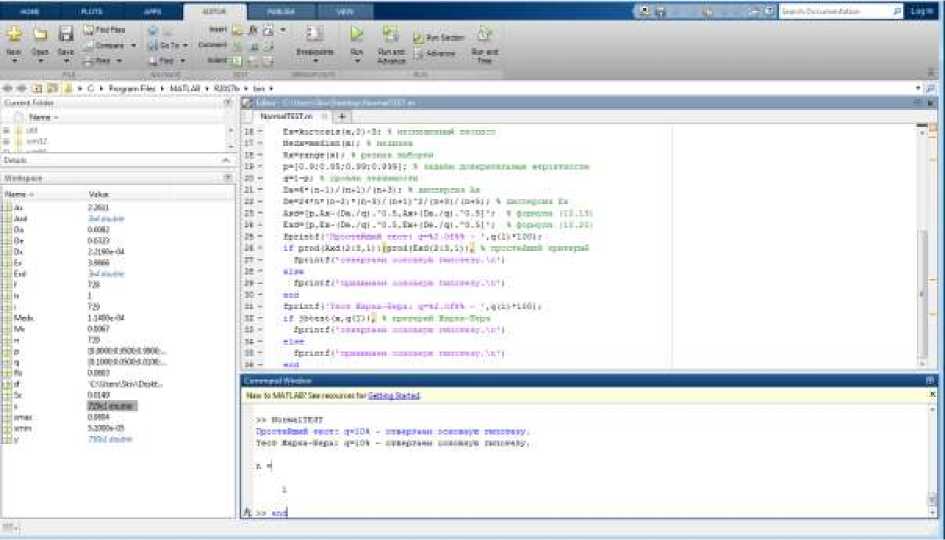
Рисунок 1. Окно MatLab с результатом

Это еще раз приводит нас к мысли о неприменимости некоторых статистических проверок по отношению к реальному сетевому трафику или же о не нормальном характере его распределения.

Дальнейшие действия направлены на выбор подходящего распределения и выбор критерия согласия, способного сравнить выборку с предполагаемым распределением.

Выбор предполагаемого распределения будем проводить методом визуального анализа гистограмм распределения нашей выборки по трафику.

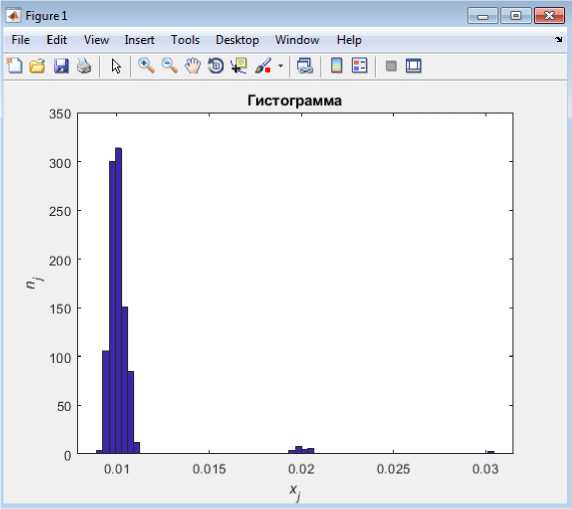
Рисунок 2. Пример гистограммы распределения

Следующим этапом мы подбираем параметры предполагаемого распределения. Для этих целей опять воспользуемся Матлаб.

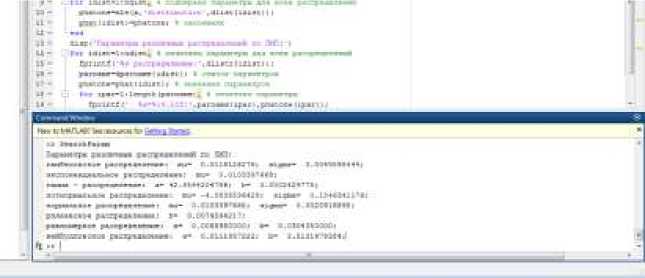
Рисунок 3. Результат подбора параметров

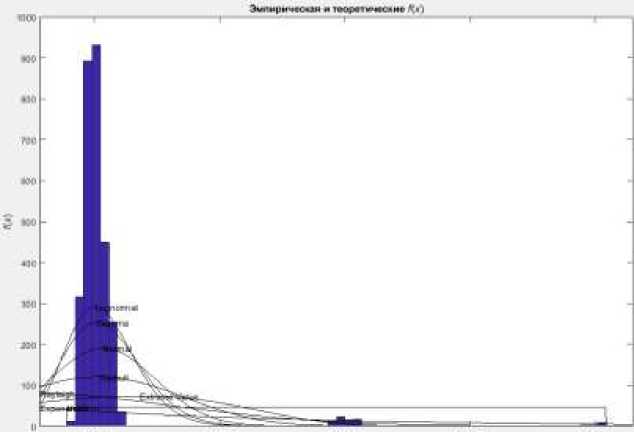
м-t             wi            ам            ем»

Рисунок 4. Построение распределений

Как видно из рисунка 4 подбор распределения под реальный трафик дело не простое и скорее всего необходимо более обширное исследование вариантов генеральной выборки. Тем не менее данный результат еще не является конечным.

Осталось проверить правильность гипотезы о принадлежности указанного трафика одному из соответствующих распределений. Для этих целей воспользуемся одним из известных критериев согласия. Критерий согласия Колмогорова. Он оптимален для наших целей так как в качестве меры различия используется максимум модуля разности между выборочной функцией распределения и теоретической. То есть критерий работает на сравнении генеральной выборки с любой другой в независимости от ее вида. Что нам и подходит. С точки зрения выборочного метода максимальная по модулю разность между выборочной и генеральной функцией:

D = max|F*(x) — F(%)|

VXER

Результат моделирования показал, что по критерию согласия Колмогорова лучше всего подходит логнормальное распределение.

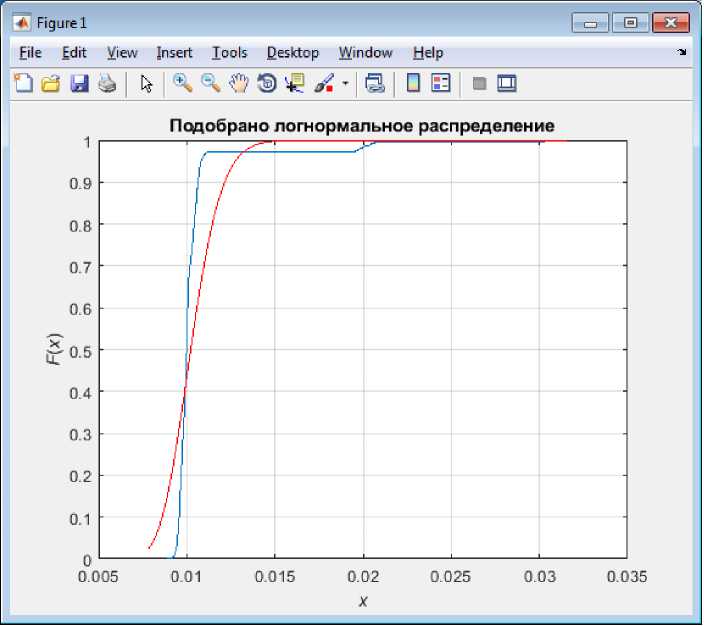
Рисунок 5. Результат