Статистические модели рыночной стоимости публичных компаний России

Автор: Берлин Ю.И., Юдкина Л.В., Коробейник В.А.

Журнал: Экономика и социум @ekonomika-socium

Статья в выпуске: 3-1 (12), 2014 года.

Бесплатный доступ

Короткий адрес: https://sciup.org/140108336

IDR: 140108336

Текст статьи Статистические модели рыночной стоимости публичных компаний России

Данное исследование продолжает опубликованные ранее Юдкиной Л.В. и Берлин Ю.И. результаты [1,2,3,4,5,6] и направлено на актуализацию регрессионных моделей формирования капитализации и стоимости российских публичных компаний на основе отчетных данных 2012 года. В частности, разработаны и представлены регрессионные модели взаимосвязи капитализации (также стоимости компаний) и стоимости активов (капитала) и собственного капитала.

Для выполнения исследования сформированы базы данных соответствующих показателей на основе публичной открытой информации, размещенной на сайтах российских компаний-эмитентов. Использовалась информация аудированной консолидированной отчетности по МСФО, а также отчетности по стандартам GAAP(США) как наиболее достоверно и полно отражающих показатели деятельности по группе в целом. Все данные по компаниям представлены в долларах США для устранения влияния рублевой инфляции. Если отчетность представлена в рублях или евро, то производился пересчет по соответствующим курсам валют по данным сайта Банка России. База данных капитализации рассматриваемых компаний сформирована на основе данных сайта Московской биржи. Данные капитализации взяты на конец каждого рассматриваемого года. В выборки включены российские компании нефтегазового сектора, энергетические компании, телекоммуникационные, горнодобывающие и металлургические, предприятия нефтехимической и химической промышленности, транспорта, автомобилестроения, потребительского сектора и др. (за исключением банковского сектора), акции которых торгуются на биржевых площадках, при наличии доступной информации о финансовых показателях по международным стандартам.

Рыночная капитализация (MC – Market Capitalization)- это произведение количества акций соответствующей категории (типа) на рыночную цену одной акции.

В качестве рыночной стоимости компании использован показатель EV (Enterprise Value):

EV = MC + ND

, где ND – чистый долг (Net Debt), или обязательства за вычетом денежных средств и их эквивалентов.

В таблицах 1-3 и на рисунках 1-2 представлены описательные статистики по исследуемым переменным.

Таблица 1 – Отраслевая принадлежность компаний, включенных в выборку

Отрасль	Число компаний		В процентах к общей сумме
Отрасль	Едини ц	В процента х к итогу	Капитализац ия	Стоимост ь компани и	Стоимост ь активов.	Собственны й капитал
Нефть и газ	5	11,4	60,3	57,4	64,2	70,0
Энергетика	17	38,6	10,8	11,6	14,4	15,4
Металлургия	6	13,6	13,5	13,5	9,3	7,3
Машиностроен ие	3	6,8	0,3	0,7	0,7	0,5
Химия и нефтехимия	4	9,1	5,0	3,7	2,2	2,1
Другие	9	20,5	10,2	13,1	9,2	4,8
Всего	44	100	100,0	100,0	100,0	100,0

Таким образом, самая многочисленная группа - это компании энергетического сектора. Их доля в выборке составляет 39 %, но доля в капитализации не превышает 11 %, а доля активов – 15 %. Компании нефтегазового сектора составляют в выборке 11,4 %, но дают наибольший вклад (от 57 до 70 %) в общую сумму каждого показателя.

В выборке присутствуют компании большой, средней и малой капитализации, а также разной степени ликвидности их акций. В связи с этим 9 компаний выборки (имеющих наибольшую капитализацию и ликвидность акций) отнесены к так называемым «голубым фишкам», таблица 2. Фактор отнесения компании к данной группе будет использован при построении моделей взаимосвязи капитализации/стоимости компании с объемом вложенного в компанию капитала.

Таблица 2 – Структура компаний по признаку «голубые фишки»

Категория «Голубые фишки»	Число компаний
Категория «Голубые фишки»	Единиц	В процентах к итогу
Да (отнесены к группе)	9	20,5
Нет (не отнесены к группе)	35	79,5
Всего	44	100,0

Таблица 3 – Описательные статистики переменных (млн. дол.)

Показател ь	Число компан ий, ед.	Миним ум	Максим ум	Средне е значен ие	Медиа на	Кварти ль 1	Кварти ль 2	Коэффиц иент вариации, %
Капитализа ция	44	17,0	112004,7	12022, 1	2231,0	654,6	11868, 3	193,1
Стоимость компании	44	317,9	209049,3	19680, 3	4737,8	1747,4	20210, 1	193,2
Стоимость активов	44	185,0	397335,1	24136, 5	5701,3	2486,8	18076, 5	259,2
Собственн ый капитал	44	-108,0	286477,5	15345, 6	3403,5	1248,7	10455, 0	291,5
Собственн ый капитал >0	43	121,0	286477,5	15705, 0	3540,0	1366,3	11090, 0	287,8

Как видно из таблицы, распределения всех показателей имеет существенную правостороннюю асимметрию (в совокупности преобладают компании со значениями рассматриваемых признаков меньшими, чем средние) и вариацию. В частности, половина представленных компаний имеют капитализацию не более 2231,0 млн. дол., 25 % компаний имеют капитализацию менее 654,6 млн. дол., а 25 % компаний - более 11868,3 млн. долларов (за счет чего среднее значение капитализации по выборки составляет 12022,1 млн. дол.).

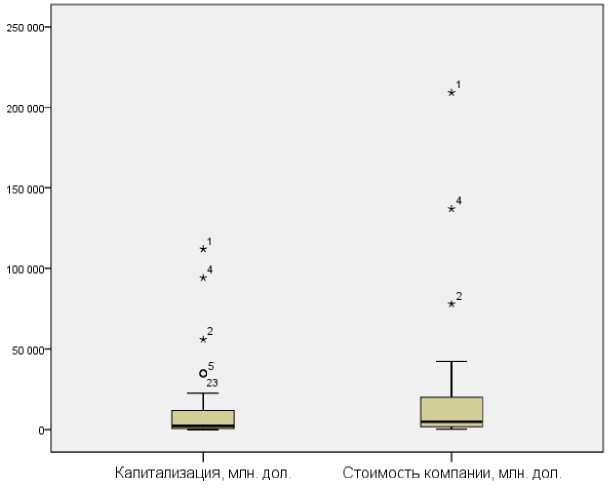
Рисунок 1 – Ящичная диаграмма компаний по капитализации и стоимости

На ящичной диаграмме рисунка 1 видно, что 3 компании имеют значения капитализации и стоимости, значительно отличающиеся от остальных: это «Газпром» (1), «Роснефть» (4) и «Лукойл» (2).

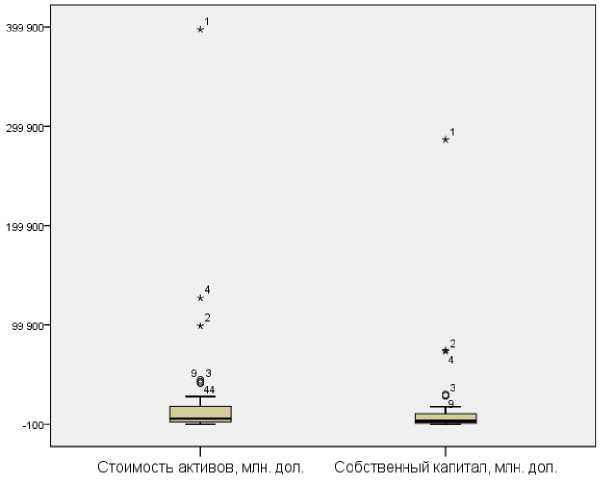
Рисунок 2 – Ящичная диаграмма компаний по стоимости активов и собственного капитала

На рисунке 2 видно, что стоимость активов компаний «Газпром», «Роснефть», «Лукойл» также значительно отличаются от других.

В таблице 4 представлены результаты проверки гипотезы о нормальном распределении изучаемых переменных.

Таблица 4 – Результаты проверки характера распределения

Критерии нормального распределения

Показатель	Колмогорова-Смирноваa			Критерий Шапиро-Уилка
Показатель	Статистика	ст.св.	Значимость	Статистика	ст.св.	Значимость
Капитализация, млн. дол.	,292	37	,000	,583	37	,000
Стоимость компании, млн. дол.	,305	44	,000	,516	44	,000
Стоимость активов, млн. дол.	,370	37	,000	,379	37	,000
Собственный капитал, млн.дол.	,384	37	,000	,347	37	,000
LN_капитализация**	,106	37	,200*	,971	37	,425
LN_стоимость компании	,118	44	,143	,970	44	,307
LN_стоимость активов	,120	37	,194	,958	37	,178
LN_собственный капитал	,089	37	,200*	,977	37	,634

* Это нижняя граница истинной значимости.

a. Коррекция значимости Лильефорса

** LN_ – натуральный логарифм соответствующего показателя

Результаты таблицы 4 показывают, что закон распределения всех показателей соответствует логарифмически нормальному (на уровне значимости 0,05). Это учтено в дальнейшем при проверке гипотез о различии компаний, а также при построении моделей влияния факторов на капитализацию/стоимость.

На рисунках 3-4 представлены результаты проверки различий по уровню капитализации, стоимости активов и финансовых результатов компаний, относящихся к разным отраслям, а также разделенных по принадлежности к «голубым фишкам». Поскольку распределения всех показателей значимо отличаются от закона нормального распределения, для проверки гипотезы о различиях будем использовать непараметрические критерии Манна-Уитни и Краскела-Уоллеса (при малой численности групп их точные аналоги).

Результаты, приведенные на рисунках 3-4, свидетельствуют о том, что капитализация/стоимость и капитал компании зависят как от отраслевой принадлежности, так и от классификации компании по признаку «голубые фишки).

Итоги по проверке гипотезы

	Нулевая гипотеза	Критерий	Знач.	Решение
1	Распределение Капитализация, млн. дол. является одинаковым для категорий Отраслевая принадлежность компании.	Критерий Крускала-Уоллиса для независимых выборок	,003	Нулевая гипотеза отклоняется.
2	Распределение Стоимость компании, млн. дол. является одинаковым для категорий Отраслевая принадлежность компании.	Критерий Крускала-Уоллиса для независимых выборок	,003	Нулевая гипотеза отклоняется.
3	Распределение Стоимость активов, млн. дол. является одинаковым для категорий Отраслевая принадлежность компании.	Критерий Крускала-Уоллиса для независимых выборок	,004	Нулевая гипотеза отклоняется.
4	Распределение Собственный капитал, млн. дол. является одинаковым для категорий Отраслевая принадлежность компании.	Критерий Крускала-Уоллиса для независимых выборок	,003	Нулевая гипотеза отклоняется.

Выводятся асимптотические значимости. Уровень значимости равен ,05.

Рисунок 3 – Результаты проверки гипотезы о различиях компаний разных отраслей по изучаемым показателям

Итоги по проверке гипотезы
	Нулевая гипотеза	Критерий	Знач.¹	Решение
1	Распределение Капитализация, млн. дол. является одинаковым для категорий «Голубые фишки».	Критерий U Манна-Уитни для независимых выборок	2,9·10^-5	Нулевая гипотеза отклоняется.
2	Распределение Стоимость компании, млн. дол. является одинаковым для категорий «Голубые фишки».	Критерий U Манна-Уитни для независимых выборок	2,4·10^-5	Нулевая гипотеза отклоняется.
3	Распределение Стоимость активов, млн. дол. является одинаковым для категорий «Голубые фишки».	Критерий U Манна-Уитни для независимых выборок	8,2 10^-6	Нулевая гипотеза отклоняется.
4	Распределение Собственный капитал, млн. дол. является одинаковым для категорий «Голубые фишки».	Критерий U Манна-Уитни для независимых выборок	1,9 10^-5	Нулевая гипотеза отклоняется.
Выводятся асимптотические значимости. Уровень значимости равен ,05.
¹Приводится точная значимость критерия.

Рисунок 4 – Результаты проверки гипотезы о различиях компаний по изучаемым показателям в зависимости от отнесения компании к «голубым фишкам»

Различия в значениях показателей для компаний, различающихся по признаку «голубые фишки», представлены на рисунке 5.

Капитализация, млн. дол.

Стоимость компании, млн.

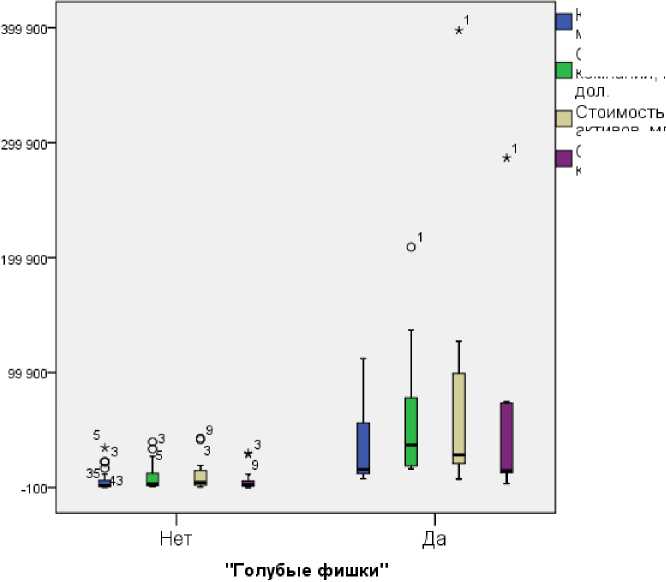
активов, млн. дол. Собственный капитал, млн. дол.

Рисунок 4 – Ящичные диаграммы по изучаемым признакам для компаний, отнесённых и не отнесенных к «голубым фишкам»

Как видно, медианные значения всех показателей у «голубых фишек» выше, чем у компаний, не имеющих такого статуса.

Апостериорные сравнения позволяют выявить, в каких именно отраслях наблюдаются различия. Результаты апостериорных сравнений приведены в таблице 5.

Таблица 5 – Попарные различия компаний разных отраслей на уровне значимости <0,05

Показатель	Имеются значимые различия на уровне значимости <0,05 между отраслями
Капитализация компании	Нефть и газ	Энергетика
		Машиностроение
		Другие
Стоимость компании	Нефть и газ	Энергетика
		Машиностроение
Стоимость активов	Нефть и газ	Энергетика
		Машиностроение
Собственный капитал	Нефть и газ	Машиностроение
		Другие

Таким образом, по уровню капитализации, стоимости компании, стоимости активов и собственного капитала имеются попарные различия в группах нефтегазовых и машиностроительных компаний. По уровню капитализации, стоимости компании и стоимости активов различаются также компании нефтегазового и энергетических секторов. Компании, отнесенные к группе «другие», также отличаются от компаний нефтегазового сектора по уровню капитализации и стоимости собственного капитала. Других попарных различий в указанных показателях у компаний, относящихся к разным отраслям, на уровне значимости 0,05 не отмечено.

Поскольку факторы «отраслевая принадлежность» и статус «голубые фишки» оказывают влияние на капитализацию и стоимость компании, они также будут учтены при моделировании.

Таким образом, в дальнейшем при моделировании зависимости капитализации от представленных факторов на основе линейного регрессионного анализа будут построены логарифмические уравнения вида:

LN(Капитализация) = Bo + Bx • LN(фактор) , что соответствует экспоненциальной зависимости:

Капитализация = e^B • фактор^в

Аналогичные зависимости моделируются для стоимости компании. В таких моделях коэффициент регрессии B 1 является коэффициентом эластичности и показывает, на сколько процентов изменяется отклик (капитализация / стоимость компании) при изменении фактора на 1 %.

Факторы «стоимость активов» и «стоимость собственного капитала» являются мультиколлинеарными (линейный коэффициент корреляции r =0.97, коэффициент роста дисперсии VIF=16,7>5), т.к. собственный капитал составляет основную долю активов. Из-за мультиколлинеарности включить оба фактора в модель не представляется возможным, поэтому будут построены однофакторные модели. Результаты моделирования представлены в таблице 6.

Таким образом, для логарифмированного отклика «капитализация компании» получена следующая модель:

ЬМ(Капитализация) = -2,262 + 1,245 • L^(Актив)

Коэффициенты модели являются значимыми на уровне 0,05; модель является адекватной (значимость F=0,000<0,05) и практически пригодной

Таблица 6 – Результаты оценки линейной регрессии для натурального логарифма капитализации, фактор – натуральные логарифм активов

Сводка для моделиb

Модель R R-квадрат Скорректиров анный R-квадрат Стандартная ошибка оценки 1 ,877a ,769 ,764 1,03311 a. Предикторы: (константа), LN_актив b. Зависимая переменная: LN_кап

ANOVA

Модель	Сумма квадратов	ст.св.	Средний квадрат	F	Знач.
1 Регрессия	149,266	1	149,266	139,853	,000
Остаток	44,827	42	1,067
Всего	194,093	43

Модель Нестандартизованные коэффициенты Стандартизованн ые коэффициенты t Знач. 95,0% Доверительный интервал для B B Стандартна я Ошибка Бета Нижняя граница Верхняя граница 1 (Констант а) LN_актив -3,262 1,245 ,947 ,105 ,877 -3,446 11,826 ,001 ,000 -5,172 1,032 -1,351 1,457 для прогнозирования (R2=76,9 %). Остатки модели на уровне значимости 0,05 удовлетворяют требованиям: имеют закон распределения, соответствующий нормальному (значимость критерия Шапиро-Уилка 0,454); нулевое среднее значение (значимость одновыборочного t-критерия 1,000); не зависят от расчетных значений (значимость линейного коэффициента корреляции 1,000).

Полученная модель соответствует уравнению:

Капитализация = 0,038 ∙ Актив1,245

Результат показывает, что при увеличении активов на 1 % капитализация компании в среднем увеличивается на 1,2 %. Средняя относительная ошибка модели составляет 13 %.

Аналогичные адекватные по всем критериям и достаточно точные модели получены для зависимости капитализации от стоимости собственного капитала, а также для описания зависимости стоимости компании от стоимости активов и стоимости собственного капитала. Результаты представлены ниже.

Таблица 7 – Результаты оценки линейной регрессии для натурального логарифма капитализации, фактор – натуральные логарифм собственного капитала

Сводка для моделиb Модель R R-квадрат Скорректиров анный R-квадрат Стандартная ошибка оценки 1 ,880a ,774 ,768 1,01415 "Экономика и социум" №3(12) 2014 228

a. Предикторы: (константа), LN_ск b. Зависимая переменная: LN_кап

ANOVA

Модель	Сумма квадратов	ст.св.	Средний квадрат	F	Знач.
1 Регрессия	144,177	1	144,177	140,180	,000^b
Остаток	42,169	41	1,029
Всего	186,346	42

Модель

Нестандартизованные коэффициенты

Стандартизованн ые коэффициенты

Знач.

95,0% Доверительный интервал для B

Стандартна я Ошибка

Бета

Нижняя граница

Верхняя граница

1 (Констант

а) LN_ск

-2,162

1,207

,859

,102

,880

-2,516

11,840

,016

,000

-3,897

1,001

-,427

1,413

Полученная модель соответствует уравнению:

Капитализация = 0,115 ∙ Собственный_капитал1,207

Результат показывает, что при увеличении стоимости собственного капитала на 1 % капитализация компании в среднем увеличивается на 1,2 %. Средняя относительная ошибка модели составляет 12,3 %.

Факторы отраслевой принадлежности, а также статуса «голубые фишки» не являются значимыми на уровне 0,05 (т.е. не влияют на уровень капитализации), поэтому в модели не включены.

В моделях взаимосвязи стоимости компании и ресурсов капитала константа не является значимой на уровне значимости 0,05, поэтому исключена из модели.

Таблица 8 – Результаты оценки линейной регрессии для натурального логарифма стоимости, фактор – натуральные логарифм активов Сводка для моделиc,d

Модель	R	b R-квадрат	Скорректированный R-квадрат	Стандартная ошибка оценки
1	,998^a	,997	,997	,51852

a. Предикторы: LN_актив
b. Для регрессии через начало координат (модель без свободного члена) R-квадрат показывает, какая доля вариабельности зависимой переменной относительно начала отсчета объясняется регрессией. Это НЕЛЬЗЯ применять к R-квадрат для моделей, включающих в себя свободный член.
c. Зависимая переменная: LN_стоим
d. Линейная регрессия через начало координат

ANOVA

Модель Сумма квадратов ст.св. Средний квадрат F Знач. 1 Регрессия 3427,936 1 3427,936 12749,620 ,000c Остаток 11,561 43 ,269 Всего 3439,497d 44 d. Эта полная сумма квадратов не скорректирована с учетом константы, так как эта константа равна нулю для регрессии, проходящей через начало координат.

Модель	Нестандартизованные коэффициенты		Стандартизованные коэффициенты	t	Знач.	95,0% Доверительный интервал для B
Модель	B	Стандартная Ошибка	Бета	t	Знач.	Нижняя граница	Верхняя граница
1 LN_актив	,981	,009	,998	112,914	,000	,964	,999

Полученная модель соответствует уравнению:

Стоимость компании = Актив0,981

Результат показывает, что при увеличении стоимости активов на 1 % стоимость компании в среднем увеличивается на 0,98 %. Средняя относительная ошибка модели составляет 4,8 %. Факторы отраслевой принадлежности и статуса «голубые фишки» также не являются значимыми на уровне 0,05 и в модель не включены.

Поскольку отраслевая принадлежность компании является переменной в номинальной шкале, для включения этого фактора в модель используем dummy-переменные, которые принимают значение 0 или 1. Коэффициент регрессии при dummy показывает, на сколько единиц в среднем отклик при данном уровне фактора отличается от значения отклика при базовом уровне фактора. За базовый уровень принят нефтегазовый сектор.

Таблица 9 – Результаты оценки линейной регрессии для натурального логарифма стоимости, факторы – натуральные логарифм собственного капитала и отраслевая принадлежность

Сводка для моделиc,d

Модель R b R-квадрат Скорректированн ый R-квадрат Стандартная ошибка оценки 1 ,998a ,996 ,996 ,59596 a. Предикторы: d6, d5, d4, d3, d2, LN_ск

b. Для регрессии через начало координат (модель без свободного члена) R-квадрат показывает, какая доля вариабельности зависимой переменной относительно начала отсчета объясняется регрессией. Это НЕЛЬЗЯ применять к R-квадрат для моделей, включающих в себя свободный член.
c. Зависимая переменная: LN_стоим
d. Линейная регрессия через начало координат

ANOVA

Модель Сумма квадратов ст.св. Средний квадрат F Знач. 1 Регрессия 3389,619 6 564,936 1590,616 ,000c Остаток 13,141 37 ,355 Всего 3402,760d 43 d. Эта полная сумма квадратов не скорректирована с учетом константы, так как эта константа равна нулю для регрессии, проходящей через начало координат.

Модель	Нестандартизованн ые коэффициенты		Стандартизова нные коэффициенты	t	Знач.	95,0% Доверительный интервал для B
Модель	B	Стандарт ная Ошибка	Бета	t	Знач.	Нижняя граница	Верхняя граница
1 LN_ск	1,026	,024	,972	43,60 3	,000	,978	1,073
d2-Энергетика	-,123	,238	-,009	-,515	,610	-,605	,360
d3-Металлургия	,626	,321	,026	1,948	,059	-,025	1,276
d4- Машиностроение	,556	,379	,016	1,468	,151	-,211	1,323
d5-Химия и нефтехимия	-,063	,350	-,002	-,179	,859	-,771	,646
d6 -Другие	,900	,276	,044	3,262	,002	,341	1,459

Таким образом, получена следующая модель (средняя относительная ошибка модели 5,1 %):

/^(Стоимость компании ) = -0,123d2 + 0,626d3 + 0,556d4 — 0,063c/5 + 0,900d6 + 1,026 • L^(Собственный_капитал),

где d2=1, если компания относится к сектору энергетики;

d3=1, если компания относится к сектору металлургии;

d4=1, если компания относится к сектору машиностроения;

d5=1, если компания относится к сектору химии и нефтехимии;

d6=1, если компания отнесена к группе отраслей «другие».

Полученные результаты говорят о том, что при изменении стоимости собственного капитала на 1 % стоимость компании в среднем увеличивается на 1,03 %. При прочих равных условиях стоимость компании из группы «другие» будет выше, чем стоимость компании нефтегазового сектора, в среднем в 2,5 раза. При прочих равных условиях стоимость компании в отраслях «энергетика», «машиностроение», «химия и нефтехимия» значимо (на уровне 0,05) не отличается от стоимости компании нефтегазового сектора. Различия в стоимости металлургических и нефтегазовых компаний имеется на уровне значимости 0,06 (с вероятностью 0,94): при прочих равных условиях стоимость металлургической компании будет выше, чем стоимость компании нефтегазового сектора, в среднем в 1,9 раза.

Полученные регрессионные модели являются адекватными и могут быть использованы для принятия стратегических решений и прогнозирования стоимости компаний в системе финансового менеджмента.

Статья