Статистические закономерности кедровых шишек для создания универсальных устройств

Введение . В настоящее время для лесного хозяйства не в полной мере решены вопросы применения средств механизации по первичной переработке кедровых шишек в местах их заготовки [1]. Вследствие чего возникла необходимость в разработке универсального устройства, выполняющего технологические операции дробления кедровых шишек и сортировки орешек. Основой конструктивных решений узлов устройства являются статистические характеристики естественных показателей размеров шишек и орешек.

Цель исследований . Определить естественные статистические размерные закономерности кедровых шишек и орешек.

Задачи исследований . Выявить степень корреляционной связи между параметрами шишки и отдельно шишки и орешков. Определить аналитическую зависимость между параметрами шишки. Построить математическую модель функциональной зависимости между шириной орешка и параметрами шишки.

Методы и результаты исследований . Был использован статистический и математический аппарат обработки экспериментальных данных кедровых шишек [2].

В качестве исходного, экспериментального материала для проведения исследований использовались шишки сосны сибирской кедровой урожая 2009–2010 гг., заготовленные в трех географических районах Красноярского края: Таежинском, Ермаковском и Манском лесничестве.

При заготовке, сборе и переработке кедровых шишек выполнялись требования «Основы рекомендаций по заготовке кедровых шишек» [1]. Для исследований был сформирован случайным образом массив кедровых шишек из урожая трех районов. Из общего массива для исследования каждого вида случайным образом были созданы массивы, элементы которых были случайны и независимы. Объем выборки для исследования определялся из условий: оценки выборочного среднего при известной и неизвестной дисперсии с относительной точности 8 = 0,05; коэффициента вариации ■д = 0,22; доверительной вероятности а = 0,95. Расчетные значения объема находились в диапазоне 15–45 единиц. Окончательно принят объем выборки n = 102 шт. из условия значимости критерия χ² Пирсона [3, 4].

Размерные характеристики кедровых шишек определялись по показателям: длина – L, диаметр – D и масса – M, ll – длина орешка, b – наибольшая ширина орешка, mm – масса орешка.

В качестве инструментальных средств использовались: электронный штангенциркуль ШЦЦ 906.821 ( с регулируемым усилия сжатия), весы лабораторные электронные VIBRACT. Относительная ошибка измерений составила: по длине шишки – 1,043; по диаметру шишки – 0,783; по массе шишки – 0,834; по массе орешка – 0,083.

При проведении исследований основные статические показатели выборок определялись при помощи пакета прикладных программ Statgrapchics 5.1.

Выборки проверялись на принадлежность нормальному распределению по критерию согласия χ ² К. Пирсона.

Для применения параметрических показателей выполним проверку исходных данных на принадлежность нормального закона распределения.

Визуальный анализ гистограмм (рис. 1) и вид аппроксимирующих кривой позволяет определить, что исходные данные имеют распределение, близкое к нормальному закону распределения с незначительной положительной асимметрией. Гистограммы симметричны относительно математического ожидания, наибольшие частоты располагаются в центре распределений и не содержит пропущенных классов и выбросов.

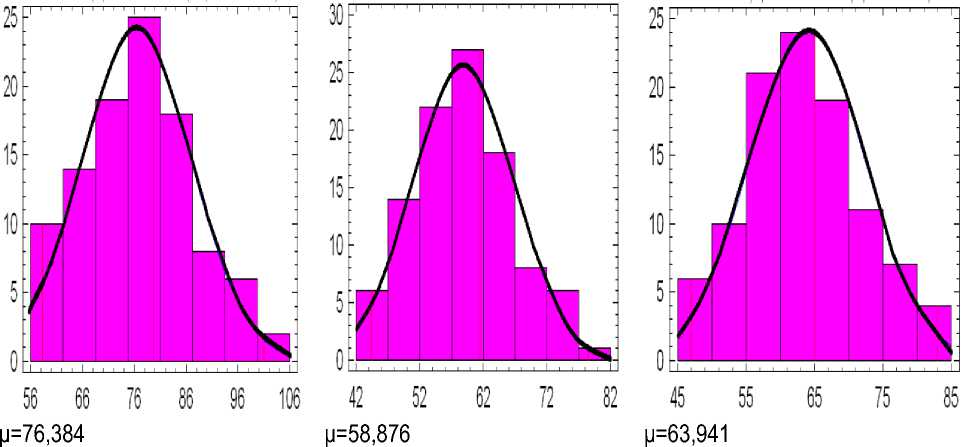
χ² р =3,11                           χ² р =2,44                          χ² р =3,28

n=102                        n=102                       n=102

Длина шишек, L             Диаметр шишек, D              Масса шишек, M

Рис. 1. Распределение шишек по основным размерным характеристикам

Расчетные значения критерия Пирсона х² р не превышают табличные значения ^х а = 0 . 05 . Полученные соотношения X 2 <  Х = 0.₀₅ позволяют с доверительной вероятностью а = 0,95 принять гипотезу о нормальном распределении размерных показателей кедровых шишек. Препятствий для применения параметрических методов статистического анализа нет [4].

На основании графических зависимостей (рис. 2–4) наблюдается корреляционная зависимость между аргументом и функцией. Статистический анализ позволил определить коэффициент корреляции r = 0,86 ÷ 0,93 и коэффициент детерминации R ² = 0,75 ÷ 0,86, что позволяет использовать для аппроксимации как линейную, так и полиноминальную регрессию второго порядка.

Дальнейшие исследования проводились для выявления парных и совокупных исходных данных статической закономерности (изменчивости) между размерными показателями шишки: L – длина шишки, D – диаметр шишки, M –масса шишки, ll – длина орешка, b – наибольшая ширина орешка, mm – масса орешка. Исходные данные параметров шишек были представлены в виде матрицы 6 × 102, из них 4 переменные измерены в одной и 2 в другой интервальных шкалах.

Выполним корреляционный анализ для оценки количественного метода определения тесноты и направления взаимосвязи между выборочными параметрами кедровой шишки и орешками. Для этой цели используем коэффициент корреляции Пирсона «r» , который отражает степень линейной связи между переменными. В общем виде выборочные коэффициенты корреляции определяются по аналитической зависимости

=

∑ t=l (   ̅)( II ̅)

√∑i=i( Xi- ̅) ²∑ ”=1( Y- ̅) ^,

где – среднее переменной Х;

^̅ – среднее переменной Y.

Для определения коэффициентов корреляции используем процедуру Multiple-VariableAnalysis стат. пакета Statgraphics. Результаты анализа отображены в матрице 6 × 6 таблицы 1.

В ячейках таблицы 1 содержатся:

– в верхней строке ячеек приведены значения коэффициентов корреляции Пирсона в виде парных значений параметров кедровых шишек;

– в средней строке – число экспериментальных данных, значения которых используются для вычисления каждого коэффициента;

– в нижней строке – значение р – уровень значимости коэффициентов корреляции.

Матрица линейной парной корреляции параметров кедровых шишек

Таблица 1

Параметр	L	D	M	ll	b	mm
L	1,0000	0,9127 102 0,0000	0,8600 102 0,0000	0,2572 102 0,0091	0,2656 102 0,0070	0,2422 102 0,0142
D	0,9127 102 0,0000	1,0000	0,9069 102 0,0000	0,2327 102 0,0186	0,2350 102 0,0174	0,2252 102 0,0229
M	0,8600 102 0,0000	0,9069 102 0,0000	1,0000	0,3172 102 0,0012	0,3310 102 0,0007	0,3083 102 0,0016
ll	0,2572 102 0,0091	0,2327 102 0,0186	0,3172 102 0,0012	1,0000	0,9595 102 0,0000	0,9134 102 0,0000
b	0,2656 102 0,0070	0,2350 102 0,0174	0,3310 102 0,0007	0,9595 102 0,0000	1,0000	0,9323 102 0,0000
mm	0,2422 102 0,0142	0,2252 102 0,0229	0,3083 102 0,0016	0,9134 102 0,0000	0,9323 102 0,0000	1,0000

Качественная оценка связи оценивается на основании парных коэффициентов корреляции (см. табл. 1), что по шкале английского статистика Чеддока оценивается как высокая и весьма высокая:

– для параметров шишки r L-D = 0,9127; r L-M = 0,8600; r D-M = 0,9069;

– для орешков r ll-b = 0,9595, r ll-mm = 0,9134, r b-mm = 0,9323;

– для параметров шишек и орешков как слабая и умеренная: r mm-L = 0,2422;

– r mm-D = 0,2252; r mm-M = 0.3083; r b-L = 0.2656; r b-D = 0,2350; r b-M = 0,3310;

– r ll-L = 0,2572; r ll-D = 0,2327; r ll-M = 0,3172.

Адекватность коэффициентов корреляции оценивается статистическим уровнем значимости, a= p. Уровень значимости – показатель, который находится в убывающей зависимости от доверительной вероятности P. Большему значению уровня значимости a=p соответствует низкий уровень доверительной вероятности P, низкому значению a = p – высокому уровню доверительной вероятности P. Соотношение между уровнем значимости и доверительной вероятности выражается зависимостью a=1-p,

где a – уровень значимости;

P – доверительная вероятность.

Уровень значимости для параметров шишки и орешков принимают значения P < 0,05 , которые соответствуют статически значимым ненулевым корреляциям на уровне достоверности (с доверительной вероятностью), соответствующей P = 0,95.

Согласно расчетным количественным показателям (см. табл. 1), между размерными параметрами шишки: длины L, диаметра D и массы М и отдельно для орешков: длины ll, ширины b, массы mm, – существует высокая и весьма высокая корреляционная зависимость, на основании которой можно предположить о существовании объективной природно-причинной связи. Корреляционная зависимость между параметрами шишки и орешков относится к слабой и умеренной, которая приводит к большей изменчивости размерных показателей шишки и орешек. Другими словами у шишки большой длины и ширины могут быть мелкие орешки и наоборот.

Для получения функциональной зависимости размерных параметров кедровых шишек выполним регрессионный анализ [3].

Графическое отображение линейной и полиноминальной функций между показателями шишек представлено на рисунках 2–4.

Линейные модели, приведенные на рисунках 2–4, согласно дисперсному анализу при уровне значимости p< 0,01, соответствуют статистически значимым соотношениям между L и D, M и D, М и L с доверительной вероятностью 0,99. Высокие значения коэффициентов корреляции r L-D = 0,93, r M-D = 0,92, r M-L = 0,75 соответствуют высокой и весьма высокой качественной оценке связи между параметрами в линейной модели.

ШИШКИ

L = 3,71702 + 1,23424D r = 0,93

L = 26,19 + 0,471583D + 0,00635705D2

R2= 0,86

Рис. 2. Линейная и полиноминальная функции взаимосвязи длины (L) шишек от диаметра (D)

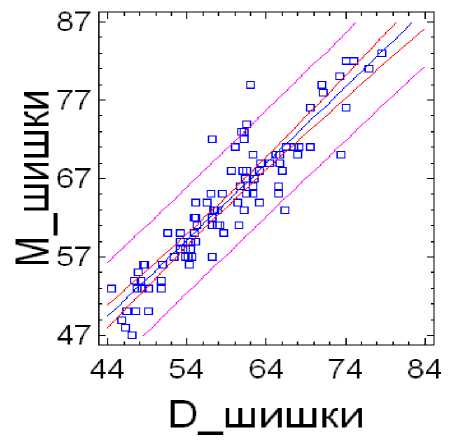
M = 6,47665 + 0,976027D r = 0,92

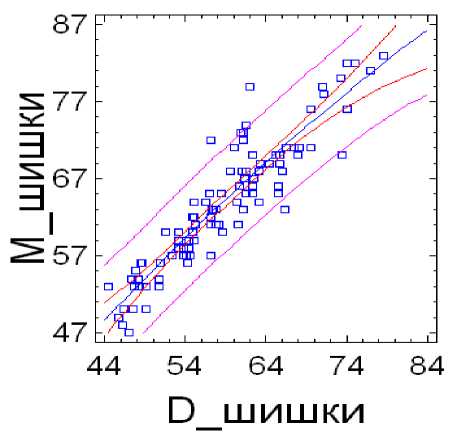
M=–8,11302+1,47115D–0,00412706D2

R2= 0,84

Рис. 3. Линейная и полиноминальная функции взаимосвязи массы (M) шишек от диаметра (D)

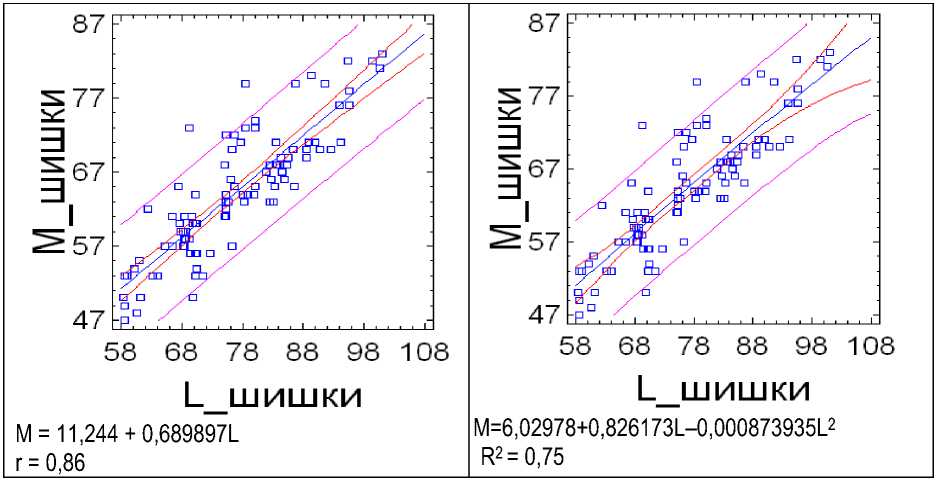
Рис. 4. Линейная и полиноминальная функции взаимосвязи массы (M) шишек от длины (L)

Коэффициент детерминации этих моделей находится в границах R2 = 0,86; 0,85, 0,74 и объясняет все изменчивости в данных общими факторами L = f(D), M = f(D), M = f(L) с вероятностью 0,86; 0,85; 0,74, с вероятностью 0,16; 0,15; 0,26 связана изменчивость неустановленных факторов.

Полиноминальные модели второго порядка, приведенные на рисунках 2–4, значимы с доверительной вероятностью, равной 0,99 при уровне значимости 0,01. Коэффициент детерминации этих моделей находится в границах R2 = 0,86; 0,84; 0,75 и объясняет изменчивость общими факторами L = f(D), M = f(D), M = f(L) с вероятностью 0,86; 0,84; 0,75, с вероятностью 0,14; 0,16; 0,25 связана изменчивость неустановленных факторов.

Выполненные исследования дали возможность установить устойчивые статистические зависимости на качественном и количественном уровне между параметрами кедровой шишки и орешков, которые позволяют получить обобщенную зависимость изменения ширины орешка «b» в зависимости от параметров шишки в целом методом многофакторного линейного регрессионного анализа. Данные исследования позволяют решить ряд задач прикладного характера при разработке сортировочного узла устройства.

Многофакторный регрессионный анализ используем для получения статистической зависимости ширины орешка «b» (зависимой величины – функции) от размерных величин и весовых значений кедровых шишек и орешков, выбранных независимыми аргументами [3] (табл. 2).

Результат построения многофакторной линейной модели для «Ь» (множественный регрессионный анализ)

Таблица 2

Независимая переменная	Оценка коэф.ур-ния	Стандартная ошибка	t-статистика	p-значение
Свободный член	–0,69492	0,319674	-2,17384	0,0322
Длина шишки, L	0,0030959	0,0042132	0,734804	0,4642
Ширина шишки, D	–0,0091481	0,0069248	-1,32105	0,1896
Масса шишки, M	0,0065414	0,0053291	1,22747	0,2226
Длина орешка, ll	0,599683	0,0572522	10,4744	0,0000
Масса орешка,mm	7,09631	1,29629	5,47431	0,0000

Результаты аппроксимации многофакторной регрессионной модели d = f(L, D, M, ll, mm):

– коэффициент детерминации R2= 0, 9411;

– коэффициент детерминации R2 (с поправкой на D.F.) = 0,9380;

– стандартная ошибка Est. = 0,180739;

– средняя абсолютная ошибка = 0,14075.

Полученная функциональная модель в виде многофакторной линейной аналитической зависимости имеет вид b = – 0,694921 + 0.003096*L – 0.009148*D + 0.006541*M+ +0,59968*ll + 7,09631*mm.

Из таблицы 3 дисперсионного анализа следует, что модель информационно способна, так как коэффициент детерминации параметра «b» достаточно большой, R2-квадрат = 0, 9380. Значение «b» с доверительной вероятностью 0,9380 обусловлено влиянием контролируемых факторов: L, D, M, ll, mm. Модель значима, так как критерий Фишера F = 306,6 >F 0,001 (уровень значимости p< 0,001). Поскольку p-значение в таблице меньше 0,001, то статистически значимая взаимосвязь между переменными соответствует доверительной вероятности = 0,999.

Таблица 3

Результат построения многофакторной линейной модели для «b» (дисперстный анализ)

Источник	Сумма квадратов отклонений	Число степеней свободы	Средний квадрат	F-отношение	p-значение
Модель	50,0658	5	10,0132	306,6	0,0000
Остаток	3,1360	96	0,0327
Всего	53,2018	101

Выводы. На основе статистической обработки экспериментальных данных для кедровых шишек в целом были определены естественные статистические закономерности в виде аналитических зависимостей:

• 1)    установлена корреляционная связь, которая оценивается парными коэффициентами связи параметров шишки и орешков как высокая и весьма высокая, связь между шишками и орешками слабая и умеренная;

• 2)    определены аналитические выражения параметров шишки в виде линейной и квадратичной зависимости;

• 3)    получена математическая модель функциональной зависимости на основе многофакторной линейной регрессии между шириной орешка и параметрами шишки.