Статистический анализ IP и VOIP трафика

Анализ статистических данных трафика в различных типах сетей с пакетной коммутацией выявил некоторую общность его свойств.Сходство заключается в том,что поток информации состоит из повторяющихся, «похожих» друг на друга фрагментов. Вероятность появления той или иной случайной величины в пределах одного фрагмента (базовой структуры) описывается некоторым законом распределения вероятностей, причем этот закон подходит для описания остальных базовых структур. Такое свойство было названо самоподобием [4].

Целью работы является исследование доступными методами структуры реального сетевого и голосового трафиков,направленное на выявление его самоподобных свойств.

Массивы данных, рассматриваемые далее, были собраны на сети компании ЗАО «Самара Телеком» в процессе мониторинга двух клиентских каналов в течение 7 дней, потребляющих в первом случае только Internet трафик, а во втором случае только VoIP. Массивы состоят из значений, полученных суммированием числа всех переданных пакетов за каждые 15 минут. Рис. 1 иллюстрирует колебания собранной нагрузки сети от времени суток.

а)                                                   б)

Рис. 1. Зависимость нагрузки сети от времени суток: а) для IPтрафика; б) для VoIPтрафика

Анализ IP и VoIP реализаций

Анализ полученных данных производится в следующем порядке:

• -    оцениваются плотности распределения изучаемых временных рядов;

• -    оцениваются и анализируются автокорреляционные функции изучаемых временных рядов;

• -    анализируются энергетические спектры изучаемых временных рядов;

• -    оценка коэффициента Хэрста производится двумя методами: методом R / S статистики и методом периодограмм.

Вычисление автокорреляционных функций производилось по формуле

R ( k ) =

2 ( x - x )( x   - x )

i          i + k

1 i ---:----------------------------

N - т        a ² ( X )

где X – выборочное среднее ряда X , о ² ( X ) - выборочная дисперсия ряда X , k g Z ₊ = { 0;1;2... } [2]. Графики автокорреляционных функций для исследуемых временных рядов приведены на рис. 3.

б)

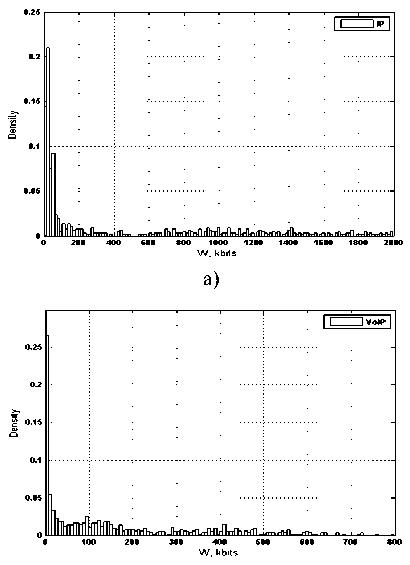
Рис. 2. Гистограммы изучаемых реализаций: а) IPтрафик; б) VoIPтрафик

а)

б)

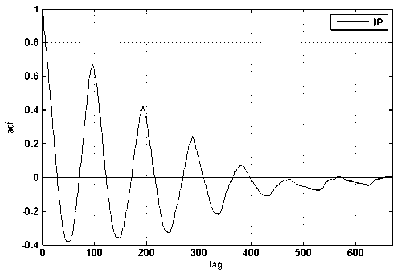
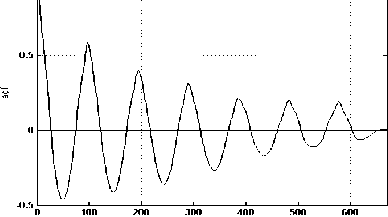
Рис. 3. Графики автокорреляционных функций: а) для IPтрафика; б) для VoIPтрафика

Произведем оценку плотностей распределения для анализируемых реализаций (см. рис. 2). Визуальный анализ гистограмм изучаемых временных рядов позволяет сделать следующие выводы:

• -    изучаемые трассы, скорее всего, подчиняются распределению с так называемым «тяжелым хвостом»;

• -    для IPтрафика характерно более равномерное распределение пакетов больших размеров (вероятность появленияпакетов размеромот1000 кбайт и до 2000 кбайт практически одинакова);

• -    для VoIPтрафикахарактерноплавноеумень-шение плотности распределения при увеличении размера пакета, причем основная нагрузка приходится на пакеты малого и среднего размера.

Из рис. 3 видно, что коэффициенты автокорреляции хоть и медленно, но все же стремятся к 0. Можно с уверенностью сказать, что процессы обладают большими последствиями, однако остается открытым вопрос об их самоподобии.

Процесс X называется асимптотически самоподобным, если для достаточно больших k автокорреляционная функция

R(k,X^{( m )}) ^ R(k,X) при m ^да , (2) где процесс X ^{( m )} получен усреднением исходного процесса по неперекрывающимся блокам размера m [1].

Таким образом, автокорреляционная функция асимптотически самоподобного процесса не вы- рождается при m → ∞ . У стохастического процесса, напротив, при m → ∞ автокорреляционная функция вырождается. Если же процесс строго самоподобен, то при усреднении по блокам размера m автокорреляционная функция вообще не меняет своего значения [3].

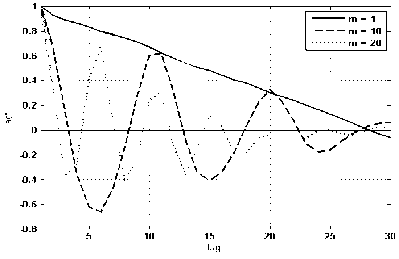
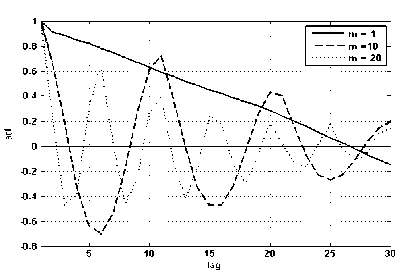
Проследим тенденцию изменения автокорреляционной функции при увеличении числа m (см. рис. 4).

а)

б)

Рис. 4. Зависимость автокорреляционной функции от m : а) IP трафик; б) VoIPтрафик

Из рис. 4 видно, что увеличение размера блока m приводит к более быстрому затуханию автокорреляционной функции, то есть необходимое условие самоподобия выполняться не будет. Однако не следует забывать о двух условиях, при которых должно выполняться (2).

Во-первых, (2) справедливо при m → ∞ . На практике это означает, что в интервал m должно попадать такое количество базовых структур, чтобы в случае попадания начала интервала m на какой-либо определенный участок базовой структуры, это не вызывало статистически значимых изменений величин усредненного процесса. Если, например, все значения из блока m _i попадут на возрастающий участок базовой структуры, то значения блока m i+1 могут попасть на убывающий участок, и значения автокорреляционной функции будут обратными [3]. Такого не случится, если блок m включает в себя достаточно большое количество базовых структур, по которым усредняется значение ряда. Таким образом, лучше исключить из анализа блоки, охватывающие лишь часть базовой структуры. Для рассмотренного примера максимальное число отсчетов, входящих в блок m = 20 , что составляет 0,2 базовой структуры. Поэтому наблюдаемая тенденция не отражает действительности.

Во-вторых, условие (2) выполняется для больших лагов автокорреляции k . Автокорреляционная функция исходного процесса (см. рис. 3) медленно приближается к 0. Автокорреляционная функция процесса, усредненного по блокам m большого размера, не вырождается. То есть, несмотря на небольшое значение автокорреляционной функции усредненного процесса в самом начале, она убывает значительно медленнее и, начиная с какого-то значения лага, ее значения будут совпадать со значениями автокорреляционной функции исходного процесса [4].

Энергетические спектры

Известно, что в частотной области медленно убывающая зависимость (МУЗ) отражается на степенном законе поведения спектральной плот-

а)

б)

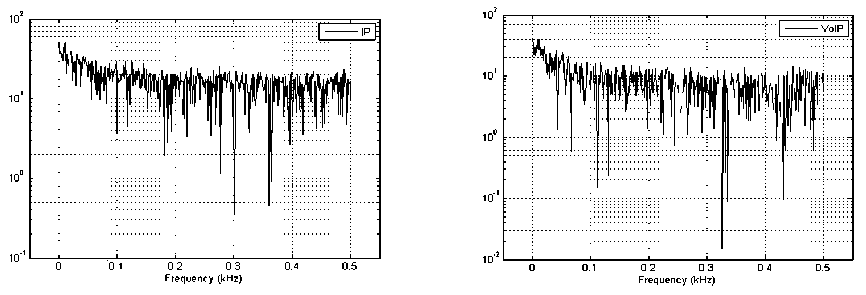
Рис. 5. Энергетические спектры реализаций трафика: а) IPтрафик; б) VoIPтрафик

ности рассматриваемого процесса. Можно констатировать, что процесс X обладает МУЗ, если

log< M

RW

S (n)

> ~ H log(n) + log(c) при n ^^ . (7)

f (X) ~ Xе-1 L2 (X), X > 0, 0< в < 1,     (3)

Таким образом, параметр Н можно оценить,

где L ₂ – медленно изменяющаяся в нуле функция, f ( X ) = V R ( k ) e ^ikX - спектральная плотность.

k

Таким образом, с точки зрения спектрального анализа, процесс с МУЗ обладает плотностью с особенностью в нуле (то есть f ( X ) процесса стремится к бесконечности, по мере того как частота λ стремится к нулю) [6].

Рассчитанные энергетические спектры реализаций представлены на рис. 5, где на оси абсцисс отложена частота λ (кГц), а по оси ординат – спектр в логарифмическом масштабе.

изобразив график log < M

R (n) S (n)

> от log(n), и, ис-

пользуя полученные точки, подобрать по методу

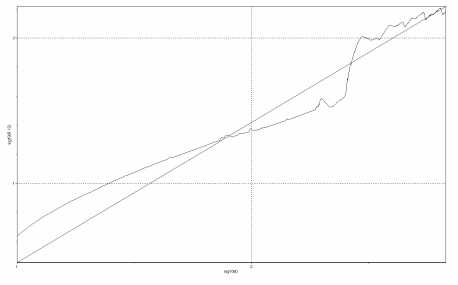
наименьших квадратов прямую линию с наклоном Н [1]. Для нашего случая получаем для IP трафика Н = 0,7655, для VoIPтрафика Н = 0,702. Графики представлены на рис. 6.

Коэффициент Хэрста

Коэффициент Хэрста Н является показателем степени самоподобия процесса, а также свидетельствует о наличии у него долговременной зависимости. В случае 0,5 <  H < 1 говорят о наличии свойства самоподобия у процесса; при 0 <  H < 0,5 самоподобным свойством процесс не обладает [2].

Оценим показатель Хэрста Н методом нормированного размаха ( R / S ).

а)

Для заданного

X = { х n , n e Z + }    с

набора наблюдений выборочным средним

1n

X = — у X j размах определяется как ⁿ j =1

R(n) = max A, - min A,,          (4)

1≤ j ≤ n ^j 1≤ j ≤ n ^j

k где д k = V Xi i=1

- kX, W = 1, n, есть разность меж-

ду максимальным и минимальным отклонением. Для описания изменчивости более удобна нормированная безразмерная характеристика:

R (n) S (n)

max A j - min A

1 <  j <  n ^J 1 <  j <  n

¹ V [ X j ⁿ j = 1

-

Хэрст назвал это соотношение нормированным размахом и показал, что справедливо следующее эмпирическое соотношение

M

R(n) S (n)

~ cn H

при n → ∞ ,

где с – положительная конечная константа, не зависящая от n . Прологарифмировав обе части (6), получим

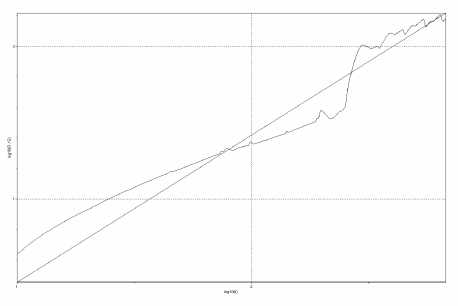
б)

Рис. 6. Графики R / S -статистики: а) IPтрафик; б) VoIP трафик

Оценка, основанная на графике спектральной плотности, составляет суть метода, который обеспечивает большую статистическую строгость, чем оценка методом нормированного размаха ( R / S ). Периодограмма (или «функция интенсивности») I N ( to ) оценивает спектральную плотность дискретного стохастического процесса Х_t и может быть оценена рядом на интервале времени N :

IN И =

2n N

N ²

V X k e»^m k = 1

to e [0; n]

где { X _k } - временной ряд; N - длина временно-

го ряда.

Учитывая, что самоподобность влияет на характер спектра S( ю ) при ю >  0 , должен получиться график зависимости спектральной плотности вида

I N ( го ) ~ [ го ] ¹ 2 H при ю >  0           (9)

Построив зависимость log [ l N ( го ) ] от log( ro ), подбирают касательную прямую линию к кривой. Наклон линии будет приблизительно равен 1 – 2 Н [1]. В нашем случае для IPтрафика Н = 0,802, для VoIPтрафика Н = 0,758. Графики представлены

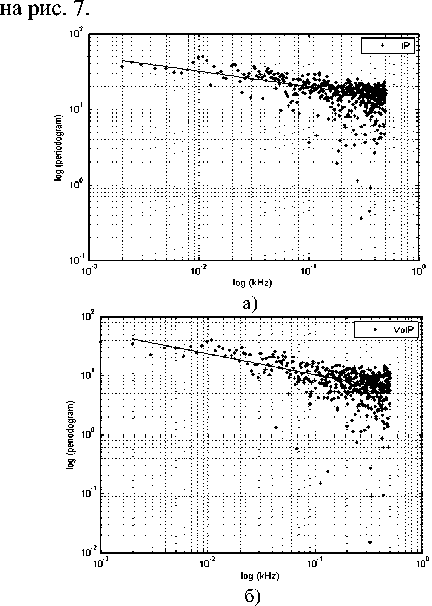
Рис.7. Графики периодограмм: а) IPтрафик; б) VoIP трафик

Выводы

Подводя итоги выполненного анализа сетевых реализаций IPи VoIPтрафиков, можно сделать следующие выводы:

• -    трассы исследуемых протоколов,скорее всего, подчиняются некоторому распределению с так называемым «тяжелым хвостом»;

• -    автокорреляционные функции исследуемых рядов имеют отчетливую периодическую структуру, а также можно сказать, что процесс обладает большим последствием;

• -    на основании результатов,полученных при из-мерениикоэффициента Хэрста Н методами R / S -статис-тики и методом периодограмм,можно отметить,что изучаемые трассы обладают свойством самоподобия.

Таким образом,исследуемые реализации можно классифицировать как сложные,похожие на случай-ные,однако предсказуемые процессы.В связи с этим увеличение эффективности обработки трафика может основываться на алгоритмах прогнозирования. Использование техники прогнозирования позволит решить ряд задач в области обеспечения заданного уровня качества обслуживания QoS,чему будут посвящены дальнейшие исследования.