Статистический анализ показателей состояния и охраны окружающей среды в Российской Федерации

Вопрос защиты окружающей среды и всех видов природных ресурсов неоспоримо является одним из главных вопросов, стоящих на мировом масштабе, так как не существует практически государства, которое бы в той или иной мере не пыталось решить данную проблему. Однако при этом возникает потребность соответствующей статистической информации. Существуют ряд различных методов и концепций анализа влияния экономической деятельности на окружающую среду, а также анализа обратного воздействия. Нередко в практике рассчитывается оценка ущерба от выбросов в окружающую среду и показатели эффективности природоохранных мероприятий.

Актуальность данной темы обусловлена тем, что нарушение естественных балансов экологии и излишняя нагрузка экосистем, как правило, становятся причинами множества необратимых процессов и являются реальной угрозой для существования и жизнедеятельности человечества. Загрязнение и перегрузка растительных, энергетических и других сырьевых ресурсов на сегодняшний день достигли лимитов возможного самоочищения и воспроизводства природы. В Мировой океан попадает около 10 млн. тонн нефти. Каждый год в атмосферу выбрасывается более 150 млн. тонн диоксида серы. Ежегодно уменьшаются площади почв, пригодных для земледелия, на 7-8 млн. гектар, в среднем из недр земли добывается до 100 млрд. тонн руды, топлива и других различных материалов, в том числе до 5 млрд. тонн нефти и природного газа.

Для расчета параметров уравнения регрессии применим табличный редактор MS Excel, результаты расчетов представим в таблице 1.

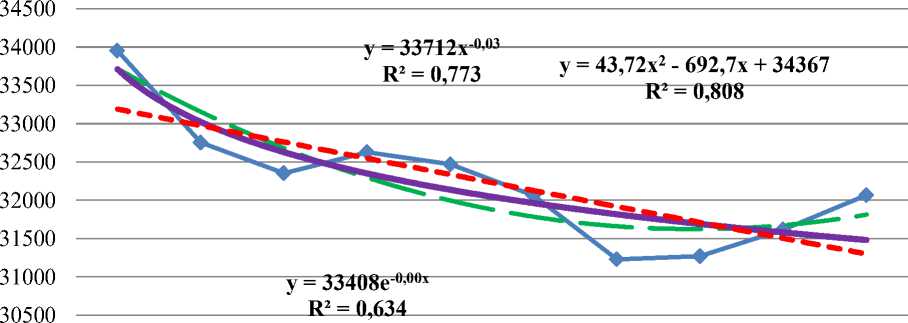
объем выброса загрязняющих атмосферу веществ

Полиномиальная (объем выброса загрязняющих атмосферу веществ) Степенная (объем выброса загрязняющих атмосферу веществ)

Экспоненциальная (объем выброса загрязняющих атмосферу веществ)

Рисунок 1 – Динамика объёма выброса загрязняющих атмосферу веществ в Российской Федерации, тренды развития

Для определения оптимального уравнения тренда необходимо обратить внимание на наибольший коэффициент аппроксимации и наименьшую среднеквадратическую ошибку.

Критерий оценки устойчивости уравнения регрессии в целом дает R2, в результате расчетов в случае параболы значение данного показателя выше, чем у прямой. Именно такой тренд будем использовать для приятия решений и прогнозирования.

Таблица 1 – Характеристики трендов развития уровня объёма выброса загрязняющих атмосферу веществ в Российской Федерации

Форма тренда	Модель	R2
Степенная	y = 33712x-0,03	0,773
Парабола второго порядка	y = 43,72x2 - 692,7x + 34367	0,808
Экспонента	y = 33408e-0,00x	0,634

По полученным данным наилучшим является полиномиальный тренд второго порядка, т.к. у него самый высокий R ².

Уравнение полиномиального тренда второго порядка объема выброса загрязняющих атмосферу веществ в Российской Федерации имеет вид:

y = 43,72x2 - 692,7x + 34367

Именно его будем использовать для прогнозирования.

F -критерий для данной модели равен:

F. = факт

—n ( n - 2 ) = 1 - R ^{2V 7}

0,808

1 - 0,808

( 10 - 2 ) = 33,67.

Так как ^табл < Fфакт, , то H0 - гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность.

Сделаем точечный и интервальный прогноз объема выброса загрязняющих атмосферу веществ в Российской Федерации на ближайшие три года (на 2018 – 2020 гг.).

Прогноз должен иметь вероятностный характер, как любое суждение о будущем. Для этого вычислим среднюю ошибку прогноза положения тренда на год за номером t _m , обозначающая m , по формуле:

1117729,80

S> = .        2   = 373'79

R (11 - 6,5)2

'      -з7.  ^-     9..        -.2

Рассчитаем доверительный интервал прогноза положения тренда по формуле:

Уточ ± 2,201 • 119,21

Прогнозирование по тренду имеет качественное ограничение: оно допустимо в условиях сохранения основной тенденции.

Таблица 2 – Прогнозные значения объёма выброса загрязняющих атмосферу веществ в Российской Федерации

Год	Нижняя доверительная граница прогноза	Объём выброса загрязняющих веществ	Верхняя доверительная граница прогноза
2018	31775,03879	32037,42	32299,80121
2019	32087,89879	32350,28	32612,66121
2020	32488,19879	32750,58	33012,96121

При сохранении наметившейся тенденции на ближайшее время, можно ожидать, что в 2018 г. объём выброса загрязняющих атмосферу веществ в Российской Федерации составит 32037,42 тыс.т., в 2019 г. – 32350,28 тыс. т., а в 2020 г. объём выброса загрязняющих атмосферу веществ в Российской Федерации составит 32750,58 тыс. тонн.

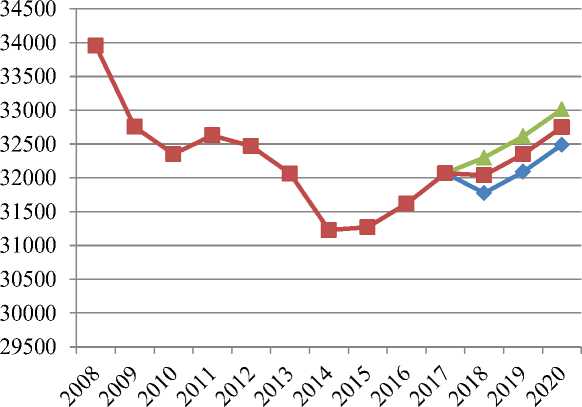
—♦—нижняя доверительная граница

—*— верхняя доверительная граница

-■- объём выброса загрязняющих атмосферу веществ

Рисунок 2 – Доверительная граница прогнозных значений объёма выброса загрязняющих атмосферу веществ в Российской Федерации

Это означает, что тренд в 2018 г. пройдет через точку с ординатой 32037,42 тыс. т., в 2019 г. – через точку 32350,28 тыс. т., а в 2020 г. – через точку 32750,58 тыс. т. Однако параметры тренда, вычисленные по ограниченному периоду, - это лишь выборочные оценки генеральных параметров. На рисунке представлена верхняя и нижняя доверительные границы прогноза.

На объём выброса загрязняющих атмосферу веществ воздействует ряд различных факторов. Попробуем изучить взаимосвязь величины объёма выброса загрязняющих атмосферу веществ и других экономических явлений, происходящих в Оренбургской области. Если закрепить влияние какого-нибудь фактора на результат и другие факторы, включенные в модель, в корреляционно-регрессионном анализе его возможно ликвидировать. В анализе временных рядов, когда тенденция закрепляется через введение фактора времени в модель в роли независимой переменной, широко используется данный прием.

Для проведения корреляционно-регрессионного анализа используем следующие факторные признаки:

• У – объём выброса загрязняющих атмосферу веществ, тыс. тонн;

Х1 – интенсивность выброса вредных веществ, г/с;

Х2 – среднее атмосферное давление, мм рт. ст.;

Х3 – средний температурный режим, оС;

Х4 – средняя влажность воздуха, %.

При помощи метода наименьших квадратов (МНК) оценим параметры модели с введением фактора времени.

Таблица 3 – Корреляционная матрица влияния факторов на объём выброса загрязняющих атмосферу веществ в Оренбургской области

	У         Х1          Х2          Х3        Х4
У Х1 Х2 Х3 Х4	1 -0,18130359             1 -0,70952893  0,247635845             1 -0,36344378  0,149721326   0,56283937              1 -0,07149155   -0,24155908   -0,41466671    -0,82339298         1

Из корреляционной матрицы между результативным (У) и факторными признаками (Х1, Х2, Х3, Х4) наблюдается значительная взаимосвязь.

ВЫВОД ИТОГОВ

Регрессионная статистика

Множественный R R-квадрат Нормированный R-квадрат Стандартная ошибка Наблюдения

0,938076 0,879986 0,783976 373,9812 10

Дисперсионный анализ

	df	SS	MS	F
Регрессия	4	5127611	1281903	9,165486
Остаток	5	699309,8	139862
Итого	9	5826921
		Стандартная	t-	P-
	Коэффициенты	ошибка	статистика	Значение
Y-пересечение	317475,2	78725,91	4,032664	0,009995
Переменная X 1	-238,17	243,3694	-0,97864	0,372704
Переменная X 2	-334,297	104,218	-3,20767	0,023791
Переменная X 3	-187,086	63,22844	-2,95889	0,031559
Переменная X 4	-287,944	72,88502	-3,95066	0,010844

Проведем регрессионный анализ. По результатам регрессионного анализа получено следующее уравнение регрессии:

у = 317475,2 - 238,17 ⋅ х - 334,297 ⋅ х - 187,086 ⋅ х - 287,944 ⋅ х

В результате построения уравнения регрессии получили следующие результаты.

Таблица 4 – Результаты построения регрессии

Показатели	Значения
Коэффициент корреляции R	0,938
Коэффициент детерминации R2	0,88
Скорректированный коэффициент детерминации R2	0,784
Фактическое значении F-критерия Фишера	9,17
Табличное значении F-критерия Фишера	2,02
Стандартная ошибка	5,11

Следовательно, построенная модель на основе её проверки по F-критерию Фишера в целом адекватна, и все коэффициенты регрессии значимы. Такая модель может быть использована для принятия решений и осуществления прогнозов.