Статистический анализ размерных характеристик пыли, образующейся при механической обработке металлов

Funding information: The research is done on theme “Development of the basics for designing integrated systems and means of operator protection from exposure to hazardous and harmful production factors” no. 5,6968,2017/БЧ within the frame of the government task of the Ministry of Education and Science of the Russian Federation in R&D.

Введение. Пыль, образующаяся при механической обработке (резании, сверлении, шлифовании, полировке и пр.) твердых металлов и сплавов способна нанести прямой или косвенный ущерб здоровью человека, привести к загрязнению природной среды. Для исключения этих негативных последствий широко используются циклоны ― устройства общей и местной очистки воздуха, использующие аэродинамический захват пыли силами инерции с последующим отсевом ее из воздушной струи в накопитель [1]. Эффективность циклонов обеспечивается расчетом, цель которого ― гарантированно уловить взвешенные в воздушной струе твердые частицы заданной категории при минимальных экономических издержках. Поскольку улавливание частиц обеспечивается за счет конкуренции инерционных и аэродинамических сил, соответствующие физические критерии составляют основу расчета циклонов [2]. Важнейшими элементами этих критериев служат размерные и массовые характеристики пылевых частиц. Вследствие естественной неоднородности производственной пыли эти характеристики имеют статистическую природу, что выдвигает жесткие требования к корректности их осреднения при расчетах систем пылеочистки (циклонов). Таким образом, достоверные научные сведения о размерных и массовых параметрах пыли при различных видах механической металлообработки являются актуальными, поскольку их практическое применение позволяет рационально организовать пылеулавливание посредством циклонов.

Машиностроение и машиноведение

Цель настоящего исследования ― отработка математических методов корректного осреднения размерно-массовых параметров пыли при механической обработке твердых металлов. Полученные результаты использовались для рационализации станка местного отсоса, а отработанные авторами математические модели и алгоритмы без существенных ограничений применимы для параметрического анализа любой пыли, подлежащей улавливанию циклонами.

Теоретические основы исследования. Пылевая частица находятся под действием силы тяжести и силы инерционной природы, которая пропорциональна массе частицы, равной р- x ³, где р — плотность образующего материала в [кг/м³]; x — характерный размер частицы в [мкм]. Следовательно, знание инерционных свойств пыли сводится к знанию ее плотности и характерного размера. Величина аэродинамической силы, действующей на такую частицу со стороны потока, пропорциональна квадрату ее характерного размера x ² и не зависит от плотности. Фигурирующее в критерии эффективности циклона отношение этих сил соответственно пропорционально комплексу р- x . Однако здесь следует учесть два важных обстоятельства: во-первых, пылевые частицы существенно отличаются по размерам и, во-вторых, форма каждой пылинки уникальна и далека от используемых эталонов (сфера, куб и др.). Эти особенности выдвигают весьма жесткие требования к процедуре двойного осреднения величины характерного размера пылевой частицы по составляющим размерам и форме. Очевидно, что методика, осредняющая характерный размер пылинок, носит целевой характер: в нашем случае она соответствует расчету эффективности циклонов.

Впервые параметрическое осреднение полидисперсных сред систематически исследовал Заутер [3, 4]. Основные результаты его работ сводятся к следующему:

• 1.    Для различных целей важны специфически осредненные средние размеры частиц из неоднородной совокупности. Поскольку средний размер представляет собой величину, выражаемую долями метра, очевидным является следующий способ размерного осреднения ансамбля частиц с функцией распределения F ( x ) и соответственно плотностью вероятности P ( x ) = dF ( x )/ dx :

• < x > у = [ j P ( x ) x i dx / j P ( x ) x dx ]^1/( i ^- j ) .                                            (1)

• 2.    Формула (1) подразумевает, что все пылевые частицы характеризуются единственным размером, т. е. имеют форму шара. Поэтому величину < x > j называют заутеровским диаметром и обозначают D ij (чаще всего под заутеровским диаметром понимается величина D 32 ).

• 3.    Если форма частиц существенно неправильна и характеризуется двумя или темя параметрами, в рассмотрение вводят также коэффициент формы. Физический смысл и практическое применение различных заутеровских диаметров приведены в табл. 1, а важные сведения о коэффициенте формы — в работе [5].

Многочисленные исследования дисперсности различных сред и материалов позволяют утверждать [6], что полученные в результате однократного дробления твердые частицы распределены по размерам согласно двухпараметрическому закону Розина — Раммлера:

F ( x , D , n ) = 1 - e^-( x / ^D ) n ,         P ( x , D , n ) = 1/ D - ( x / D ) n ^-1 - e^- x / ^D ) n ,                             (2)

где величина  = D - Г(1 + 1/ n) характеризует средний размер частиц, ап — степень размерной неоднородности ансамбля (чем меньше n, тем выше полидисперсность порошка).

При многократном измельчении порошки состоят из частиц, размеры которых удовлетворяют двухпараметрическому логнормальному распределению Гаусса — Колмогорова [6]:

• 1 ( lg x -lg D /

P ( x , D , a)  ^g e--e ^{21 lg}.                                   (3)

• V 2n - lg a - x

В распределении (3) параметр lg D отвечает условному среднему размеру частицы, а параметр lg a — разбросу реальных размеров частиц вокруг условного среднего.

Принципиальным достоинством модели Гаусса — Колмогорова является удобство пересчета величин D ij по линейным соотношениям Хэтча — Шоута [7], связывающим их с величинами D и a . Форма этих соотношений такова, что при известных двух любых величинах D nm и D_kl можно вычислить все прочие.

Важно отметить, что анализируемый авторами порошок (отходы резания рельса) не обязательно описывается приведенными здесь классическими моделями. Во-первых, технологический процесс резания содержит элементы как уникальности (каждый контакт абразивного круга с материалом рельса неповторим), так и множественности (подобные взаимодействия повторяются чрезвычайно многократно). Во-вторых, форма металлических опилок далека от сферической. Наконец, наряду с металлическими опилками, отходы резания содержат частицы выкрашивающегося абразива. Содержание последних в силу особенностей процесса и требований к инструменту может существенно различаться. Таким образом, исследование распределения отходящей пыли по размерам частиц представляется практически важной и научно значимой задачей.

Экспериментальные данные. Первичный физический анализ отходов резания осуществлялся при помощи лабораторно-измерительного комплекса Fritsch Analysette 22 Compact, использующего метод LALLS — low angle laser scattering [8]. Встроенное программное обеспечение реализует результаты измерений в первичной графической, и цифровой формах. Недостатками программной части комплекса являются: отсутствие детальных сведений об алгоритмах преобразования измеряемых величин и характере выводимых данных, а также количественные погрешности данных, отображаемых в форме графиков. В частности, может показаться, что шкала дифференциальной функции распределения (плотности вероятности) приводится на распечатках с погрешностью в несколько раз. Более глубокое рассмотрение позволяет заключить, что фактически на этом графике приведена зависимость величины P(xk) dxk от xk, причем разбиение частиц по размерам на группы шириной dxk не является равномерным. Кроме того, вычисляемые программой интегральные характеристики распределения частиц по размеру Dij не документированы, что требует их проверки на соответствие как исходным графическим данным, так и классическим моделям Розина — Раммлера и Гаусса — Колмогорова.

Отмеченные обстоятельства при оценке результатов анализа, выводимых встроенной программой, обусловливают проведение дополнительных мероприятий: нормирование исходной кривой дифференциальной функции распределения, а также проверку согласия интегральных показателей D ij как этой функции распределения, так и базовым модельным распределениям. Реализация этих задач требует высококачественной оцифровки графических результатов фракционного состава, предоставляемых прибором Fritsch Analysette 22 Compact , а для этого необходимы специализированное программное обеспечение [9, 10] и разработка надлежащих алгоритмов верификации данных.

Техника оцифровки и верификации экспериментальных данных. Для оцифровки первичных графических данных дисперсионного анализа, полученных при помощи прибора Fritsch Analysette 22 Compact , использовалась специализированная программа Grafula [11]. Этот свободно распространяемый информационный продукт позволяет перевести графически представленные зависимости в табличный вид. Процедура оцифровки сводится к считыванию графика, размещению на нем осей декартовых координат, заданию масштабов и нанесению на линию, отображающую зависимость, достаточного числа маркеров.

Результат автоматической оцифровки относится к положению введенных пользователем точек и формируется в Excel -совместимую таблицу. Погрешность получаемых в результате цифровых данных имеет несколько составляющих:

• •    погрешность формирования графика, обусловленная особенностями комплекса Fritsch Analysette 22 Compact ;

• •    дефекты печати принтером или отображения в качестве электронной фотографии (скриншота);

• •    неточности оцифровки графика программой Grafula ;

• •    невозможность достаточно точно маркировать кривую на графике вследствие ограничений как в разрешении системы, так и в психомоторных возможностях человека.

Последняя из перечисленных погрешность, по-видимому, является самой существенной. Отмеченные обстоятельства требуют дополнительных проверок результатов оцифровки с целью исключить критичные ошибки и верно оценить погрешность результата.

Для верификации результатов оцифровки данная работа выполнялась в несколько этапов. Вначале применительно к данным в нормальном по размеру частиц представлении применительно к представленным в логарифмическом масштабе, затем результаты первичного анализа сопоставлялись графически. При этом оба оцифрованных ряда подвергались перенормировке с целью исключить систематическую погрешность и обеспечить выполнение важного для функции распределения F ( x ) условия: F ( да ) = 1. Впоследствии на основе каждого из результатов строились однотипные модельные распределения, эмпирические параметры которых определялись методами математического программирования [12] и сопоставлялись. Последним этапом проверки служило сравнение рассчитанных по построенным модельным распределениям осредненных показателей размерного состава пыли с интегральными характеристиками распределений, которые выдаются программным обеспечением прибора Fritsch Analysette 22 Compact .

Машиностроение и машиноведение

Оказалось, что искажение функции распределения F ( x ) в результате невозможности извлечь ее из инструментального прибора непосредственно в цифровом представлении составляет 15 % при оцифровке графика в линейном (по размеру частиц) масштабе и 8 % при оцифровке графика в логарифмическом масштабе. О согласовании полученных двумя способами данных позволяет судить рис. 1, из которого следует, что оба восстановленных распределения практически совпадают, начиная с диаметра 10 мкм. В то же время полтора десятка первых точек, доступных для считывания с графика, имеющего логарифмическую шкалу размеров, свидетельствуют о наличии значительной доли мелких, наиболее опасных для человека частиц размером менее 10 мкм. Данное обстоятельство является второстепенным, поскольку активные системы очистки воздуха захватывают преимущественно мелкие частицы.

Тот факт, что при х ≥ 10 мкм выводимые прибором Fritsch Analysette 22 Compact в различных масштабах графические распределения совпадают, подтверждается следующей проверкой. Если аппроксимировать кривой Розина ― Раммлера оба ряда экспериментальных данных и сопоставить полученные кривые, можно количественно оценить влияние погрешности оцифровки на конечный результат.

Сравнительна оцифровка 0,04 0,03 J             С линейной шкалы размера

®   0,02             - С логарифмической шкалы размера

0,01              " * e ■ e

0 -I-----------          ' г ■ ■ t •— ■— ]

0         50        100        150        200

Диаметр частиц, мкм

Рис. 1. Результаты оцифровки данных дисперсионного анализа металлоабразивной пыли

Для аппроксимации моделью (2) сравниваемых данных, представленных на рис. 1, численно решалась оптимизационная задача, относящаяся к математическому программированию [12]. Минимизировалась невязка между фактическим и теоретическим распределениями частиц по размерам. Если невязку определять по удобной для вычислений декартовой норме, требуется минимизировать функционал:

Ф(х, D, n) = ∑[P(xk,D,n)-Pk]2 → min, k где k ― номер узловой (табличной) точки; Pk ― значение экспериментальной плотности вероятности; D и n — описанные выше параметры модельного распределения Розина ― Раммлера.

Решая эту задачу средствами Excel , получаем следующий результат. Для данных, полученных с графика линейного по х , величины D и n равны соответственно 48,37 мкм и 1,588 мкм. При этом аппроксимирующая Р ( х , D , n ) кривая характеризуется средней невязкой с экспериментальными точками 0 00274 и коэффициентом корреляции 0 894. Аналогично решая задачу для 35-ти правых точек, восстановленных с логарифмического по размеру графика, получаем значения D = 48,61 мкм, n = 1,346, невязка ― 0,00187, коэффициент корреляции ― 0,934. Близость параметров D и n для обеих таблиц совместно с малой невязкой и высокой корреляцией свидетельствуют о примерной равноценности исследованных графических образов анализируемого результата. Об отличии представления данных в формульном виде, полученных из сравниваемых графических источников, позволяет судить корреляция функций Р ( х , D , n ) с вычисленными и приведенными выше значениями параметров. Ее величина равна 0,99.

Поскольку важны размерные характеристики пыли, осредненные на основании некоторого реалистичного распределения, вычислим набор показателей Dij согласно инициализированной выше модели Розина ― Раммлера при значениях параметров D и n , полученных разными способами. Затем сравним результаты между собой и с интегральными показателями D ij , которые регистрируются прибором Fritsch Analysette 22 Compact .

Цель сравнения анализируемых графических распределений с регистрируемыми прибором интегральными показателями D ij ― выяснить, какое именно распределение приведено на этих графиках. То обстоятельство, что на экране прибора Fritsch Analysette 22 Compact величина D 43 совпадает со среднеарифметическим диаметром в пяти десятичных знаках, а величина D 32 ― со среднегеометрическим размером столь же точно, позволяет предположить, что по ординате графика регистрируется не параметр P ( x k ), а дифференциал взвешенной на x 3 функции распределения:

dF ( x k ) = P ( x k ) x k ³ dx k .                                                (4)

Это обстоятельство является ключевым при интерпретации результатов размерного анализа пылевых частиц на основе распечатанных прибором гистограмм. Проверим предложенную гипотезу, рассчитав моменты D ij . Результаты сравнения расчетов при принятии или отвержении гипотезы авторов с соответствующими числовыми данными, регистрируемыми прибором Fritsch Analysette 22 Compact , приведены в табл. 1.

Таблица 1

Диаметр, мкм	Гипотеза (4) не верна		Гипотеза (4) верна		Числовые данные прибора, мкм
	D = 48,4 мкм, n = 1,588	D = 48,6 мкм, n = 1,346	D = 48,4 мкм, n = 1,588	D = 48,6 мкм, n = 1,346
D 43	90,2	107,1	43,4	44,4	43,5
D 42	83,2	97,9	30,4	27,5	20,9
D 41	75,2	87,1	15,6	12,5	8,18
D 40	65,5	73,6	7,61	6,11	4,23
D 32	76,7	89,5	21,3	17,0	10,0
D 31	68,6	78,5	9,38	6,62	3,55
D 30	58,9	64,9	4,26	3,15	1,95
D 21	61,4	68,8	4,13	2,57	1,25
D 20	51,6	55,2	1,90	1,35	0,66
D 10	43,4	44,4	0,88	0,71	0,59

Сопоставление заутеровских диаметров пыли на основе аппроксимаций оцифрованных графических данных

Как видно из таблицы, гипотеза о сути данных, полученных с помощью сервисной программы Fritsch Analysette 22 Compact , верна. Это заключение является принципиальным при интерпретации результатов размерного анализа пыли.

Результаты статистического анализа графических данных и их интерпретация. Чтобы лучше описать мелкодисперсную часть пыли воспользуемся графическими данными (рис. 1) в логарифмическом масштабе размера и аппроксимируем их пятипараметрическим распределением, отвечающим взвешенной сумме двух логнормальных распределений:

P ( x , D 1 , D 2 , d, ^ 2 , a ) = -g=- ■ + —

V2n^ x L°"i c2

_ 1 (lg x-1g D f                 | ( 1g x-1g D2 V a^ e 21 1gai J + (1-a) ■ e 21 1ga2 J

где D 1 и D ₂ — положение пиков, o 1 , g ₂ — ширина пиков, a — доля частиц, приходящихся на первую моду.

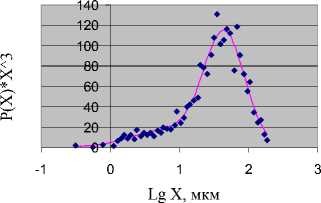
Решение соответствующей оптимизационной задачи средствами Excel дает следующий результат: D1 = 45,2 мкм, D2 = 7,0 мкм, о1 = 1,97 мкм, с2 = 2,1 мкм, a = 0,858. Средняя невязка между аппроксимирующей функцией и исходными данными составляет 31 %, а коэффициент корреляции ―  0,977. Это удовлетворительное соответствие, учитывая высокую погрешность экспериментальных значений (рис. 1). Отметим, что этот результат относится к взвешенной на х3 истинной функции распределения пыли по размерам. Трактовать его можно следующим образом: основную массу пыли (около 85 %) составляют частицы размером более 10 мкм, поэтому для практической очистки воздуха это распределение можно заменить двухпараметрическим логнормальным (2) с параметрами: D = D 1 = 45,2 мкм и a1 = а1 = 1,97 мкм. Однако, такое упрощение не позволит качественно аппроксимировать Dij с j < 3, в то время как учет мелкой фракции важен для некоторых приложений, например, для вычисления всех используемых диаметров Dij и моментов функции распределения P(x). Ниже приведены результаты сопоставления двойной логнормальной и логнормальной аппроксимаций P(x). На рис 2 представлена аппроксимация экспериментальных данных двойным логнормальным распределением:

1 ( lg x -1,65 f                    1 ( lg x -0,898 f

_T’I                  I                                ~T'I                     I

P ( x ) = 0,176 ^ e ² ^ °'⁴¹⁶ ' + 0,563 ^ e ² ^ ⁰ ' ⁷⁹¹ ' .

Среднеквадратичная относительная погрешность составляет  0,31,  коэффициент корреляции с экспериментальными точками ― 0,977.

Машиностроение и машиноведение

Двойное логнормальное ненормированное

Эксперимент

Аппроксимация

Рис. 2. Аппроксимация экспериментальных данных двойным логнормальным распределением

На рис 3 представлена аппроксимация экспериментальных данных логнормальным распределением: 1 ( lg x -1.63 7

P ( x ) = 0.563 - e ^{2 1 11435 1} .

Среднеквадратичная относительная погрешность составляет 1,23, коэффициент корреляции с экспериментальными точками — 0,970.

Логнормальное ненормированное

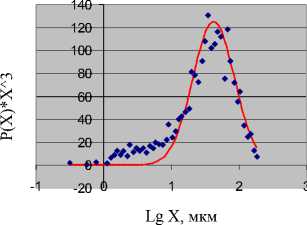
Рис. 3. Аппроксимация экспериментальных данных логнормальным распределением

Эксперимент

Аппроксимация

Также изучалась возможность приблизить экспериментальные данные распределениями Розина ― Раммлера:

• •    классическим обобщенным трехпараметрическим:

P ( x , D , n, m ) = ( x I D ) m - e^{- x /} D ) n / J ( x I D ) m - e^{- x /} D ) n ^x );

• •    упрощенным экспоненциальным:

P ( x ) = 1/ D - e^{- x 1 D} , n = 1.

На рис. 4 представлена аппроксимация экспериментальных данных распределением Розина — Раммлера:

P ( x ) = 7,73 - 10^-3 - x ^0.322 - exp[-( x /48,89)^1.322].

Среднеквадратичная относительная погрешность составляет  0,47,   коэффициент корреляции с экспериментальными точками — 0,972.

На рис. 5 — аппроксимация экспериментальных данных трехпараметрическим распределением типа Розина — Раммлера:

P ( x ) = 6,66 - 10^-3 - x ^0.4 - exp[-( x /66,18)^1.235].

Среднеквадратичная относительная погрешность составляет 0,51, коэффициент корреляции — 0,972.

Розина- Раммлера ненормированное

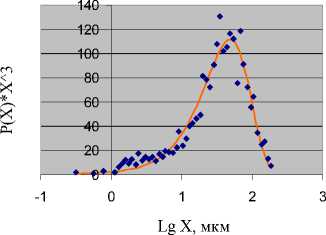
Рис. 4. Аппроксимация экспериментальных данных распределением Розина — Раммлера

Эксперимент

Аппроксимация

Трехпараметрическое типа Розина - Раммлера ненормированное

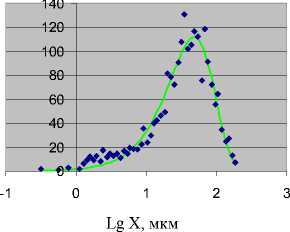
Рис. 5. Аппроксимация экспериментальных данных трехпараметрическим распределением типа Розина — Раммлера

Эксперимент

Аппроксимация

Из проведенного анализа следует, что для задач, отличных от расчетов циклонов, экспериментальные данные авторов удобно аппроксимировать однопараметрической монотонно убывающей функцией: P ( x ) = 1/ D - e^- x / D На рис. 6 представлена аппроксимация экспериментальных данных экспоненциальным распределением P ( x ) = 1/47.13 - e^- x ^/47.13. Среднеквадратичная относительная погрешность составляет 0,42, коэффициент корреляции с экспериментальными точками — 0,948.

Розина - Раммлера при n = 1 -экспоненциальное ненормированное

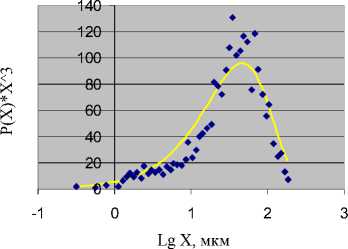
Рис. 6. Аппроксимация экспериментальных данных экспоненциальным распределением

Эксперимент

Аппроксимация

В табл. 2 приведены интегральные показатели дисперсности пыли, рассчитанные на основе модельных распределений в сопоставлении с оцененными программными средствами прибора Fritsch Analysette 22 Compact . Модельные распределения инициализированы по графическим данным.

Машиностроение и машиноведение

Таблица 2

Интегральные показатели дисперсности пыли

Параметр	Математическая модель, использованная для оценки					Фактическое значение
	о о о к о	о о о в о в о о в >в о Й	со X! & а	о 1=5 S S св л S о рц	о й к о о Г)
D 43 , мкм	51,7	44,8	44,7	45,2	43,6	43,5
D 42 , мкм	41,2	23,0	27,3	28,1	21,4	20,9
D 41 , мкм	32,0	9,45	12,2	12,9	8,61	8,18
D 40 , мкм	25,0	4,87	5,99	6,32	4,40	4,24
D 32 , мкм	32,8	11,8	16,6	17,5	10,3	10,0
D 31 , мкм	25,2	4,34	6,4	6,92	3,79	3,55
D 30 , мкм	19,6	2,32	3,07	3,28	2,03	1,95
D 21 , мкм	19,4	1,59	2,46	2,74	1,39	1,25
D 20 , мкм	15,1	1,03	1,32	1,42	0,904	0,858
D 10 , мкм	11,8	0,666	0,704	0,738	0,586	0,588
Мода, мкм	52,1	45,2	48,9	48,4	43,9	43,4
СКО σ , мкм	35,0	37,2	33,6	33,8	39,9	35,7
Асимметрия	1,49	1,17	1,19	1,20	1,41	1,25
Эксцесс	2,28	1,49	1,46	1,50	1,66	1,66

Данные рис. 4–6 и табл. 2 позволяют сопоставить соответствующие результаты между собой и с данными аппроксимации логнормальной и двойной логнормальной функциями. Эти результаты свидетельствуют о близком качестве аппроксимации, достигаемом с использованием пятипараметрического двойного логнормального, трехпараметрического типа Розина ― Раммлера, двухпараметрического классического типа Розина ― Раммлера и однопараметрического экспоненциального модельных распределений P ( x ). В то же время логнормальное распределение не соответствует опытным данным, поскольку не отражает присутствие в пыли существенной числовой доли очень мелких частиц. Вместе с тем это распределение лучше прочих соответствует практической цели работы ― оптимизации системы воздухоочистки.

Аппроксимация однопараметрической монотонно убывающей функцией P ( x ) = 1/ D ⋅ e^– x / D демонстрирует хорошее согласие с экспериментом для малоразмерных фракций пыли, которые вследствие представительности существенно влияют на среднеквадратичную относительную погрешность аппроксимации.

Выводы. Выполненный авторами анализ экспериментальных данных относительно распределения образующихся при резании рельса частиц по размерам сводится к следующему:

• 1.    Прибор Fritsch Analysette 22 Compact не является оптимальным для исследования фракционного состава пыли поскольку не представляет данных измерений в первичной числовой форме. Оцифровка предоставляемых этим прибором графиков служит главным источником погрешности в интерпретации соответствующих данных.

• 2.    Для детального анализа распределения пылевых частиц по размерам на основе доступных (имеющихся у авторов) экспериментальных данных лучше прочих подходит простейшее экспоненциальное распределение частиц по размерам P ( x ) = 1/47,13 ⋅ e^– x /47,13. . На основе этого распределения можно верно воспроизвести все интегральные показатели, предоставляемые инструментальным измерительным комплексом, наряду с графическими данными.

• 3.    Задачи воздухоочистки требуют использовать классическое логнормальное распределение:

• 4.    Ввиду того, что на эффективность циклона влияет не только величина D 32 , но и плотность дисперсного материала, состоящего из стали и абразива, для обеспечения эффективности воздухоочистки требуется уточняющий анализ. Его предметом является раздельное исследование дисперсности металлической и абразивной пыли, возникающей в результате работы рельсорезного станка.

_ 1 Г lgx-1.63 Y P(x) = 0,563- e '0435 X , параметры которого вычислены авторами методами математического программирования. Они позволили рассчитать важную для проектирования циклонов величину D32 = 32,8 мкм, втрое превышающую числовое значение, выдаваемое прибором Fritsch Analysette 22 Compact. Это означает, что ориентация в расчете циклона на предоставляемые названным прибором числовые значения приведет к неспособности удалять из рабочей зоны практически все крупные частицы.