Статистический анализ результатов педагогического эксперимента с использованием номограмм

Педагогический эксперимент — основной метод «экспериментальной» педагогики, в ходе которого исследователь получает новые опытные данные, характеризующие изучаемое педагогическое явление, ставит и решает задачи оценки эффективности методов обучения и воспитания [1].

Планируя педагогический эксперимент, педагог определяет объект исследования, педагогические методы воздействия на него, описывает средства измерения результатов эксперимента. Объект измерения в педагогике — человек. В экспериментах это не абстрактное человеческое сообщество, а вполне конкретное множество людей, связанных одним учебным процессом, образованием, возрастом и т. п.

Среди бесконечного множества характеристик этого объекта нас будут интересовать только числовые переменные. Традиционно они подразделяются на индикаторы (их можно измерить непосредственно в ходе эксперимента) и латентные (скрытые, неявные) переменные (их невозможно измерить непосредственно). Математической (иногда метрической) моделью эксперимента называется связь или выражение индикаторов через латентные переменные (см. [2, 3]). Присвоение конкретных значений индикаторам производится в ходе специальной измерительной процедуры, в роли которой выступают тестирование, экзамен, контрольная работа и т. п. При необходимости достичь высокого качества педагогических измерений к подобным процедурам необходимо предъявлять общепринятые требования: объективность, полнота, воспроизводимость, непротиворечивость и многие другие. В данной работе мы не будем на этом останавливаться подробно, подразумевая выполнение всех необходимых требований.

Важно отметить, что числовое значение, присвоенное индикатору, представляет собой отметку на определенной шкале. Широко известны номинальная (наименований), порядковая (ранговая), интервальная (количественная) шкалы, шкала отношений (или пропорциональная шкала). В отдельных случаях приходится конструировать нелинейные шкалы, наиболее подходящие для данного эксперимента.

Сама формулировка цели эксперимента приводит нас к пониманию того факта, что проверка гипотез будет иметь статистический характер и будет проводиться статистическим методом. В педагогических экспериментах это основной математический метод исследования. Его теоретическая посылка — представление о бесконечной генеральной совокупности. В математической статистике это понятие является абстракцией, отражающей представление, что эксперимент можно повторять бесконечно много раз. При этом предполагается, что относительная частота интересующего нас события обладает свойством статистической устойчивости, более того, при неограниченном возрастании объема выборки эта частота приближается к некоторому «истинному» значению [4, с. 165].

Однако эти предположения именно в педагогических экспериментах вызывают обоснованную критику. Причин здесь несколько: весьма ограниченные объемы выборок, слабая воспроизводимость результатов педагогических экспериментов, имеющая место из-за «человеческой» природы как объекта измерения, так и «прибора» измерения. Указанные обстоятельства иногда приводят исследователя к получению недостоверных результатов обработки данных, слабо обоснованных выводов, а то и к вульгаризации итогов исследования.

Статистический подход приводит к построению эмпирического распределения оценок, выделения интервалов, которым будет присвоена одинаковая итоговая оценка. При этом в исследованиях выдвигаются гипотезы о том или ином теоретическом распределении, которым якобы соответствуют полученные гистограммы, оцениваются параметры, проверяются критерии согласия и однородности, вычисляются доверительные вероятности и т. п. Все это, так или иначе, строится на предположении о статистической однородности результатов эксперимента и нормальности всех используемых распределений. Как уже отмечалось, эти предположения вызывают обоснованную критику и должны проверяться специальными процедурами.

Математические методы обработки данных и проверки статистических гипотез весьма развиты, разнообразны, однако содержат трудоемкие процедуры, включая табличные вычисления специальных функций. Здесь мы предложим алгоритмы, используемые в наиболее часто встречающихся в практике педа- гогических экспериментов статистических процедурах, но в которых вместо таблиц специальных функций используются вычислительные номограммы. При этом предварительные вычисления сведены к минимуму и могут быть осуществлены на обычном калькуляторе.

Номография — раздел вычислительной математики, в котором «инструментом» вычисления является специальный график (номограмма) и, возможно, геометрическое «устройство» — линейка [5]. Номограмма позволяет не только (и не столько) получить числовой результат, сколько по ходу решения провести минимальное исследование зависимости переменных величин, участвующих в задаче. Точность, достижимая в номограммах (2—3 верных цифры), вполне достаточна для приложений. Тезис «Цель расчетов — понимание, а не числа», безусловно, должен лежать в основе любого исследования педагогических данных.

Многочисленные справочники по математической статистике (см., например, [6]) содержат алгоритмы вычислений и подробные таблицы специальных функций распределений : нормального, Стьюдента, Фишера, хи-квадрат, но в них нет ни одной номограммы. По таблицам трудно даже для специалиста проанализировать соотношение между точностью оценок и их достоверностью. Число, считанное из таблицы или подсчитанное одним из мощных пакетов анализа статистических данных (SPSS, Statistika и пр.), представляется безапелляционной истиной, не подлежащей ни обсуждению, ни уточнению.

Первым алгоритмом статистической обработки педагогических данных часто является процедура проверки гипотезы о принадлежности экспериментальной выборки генеральной совокупности с нормальным распределением. Необходимость проверки этой гипотезы вызвана тем, что большинство статистических методов принятия решений основаны на предположении о нормальности распределений случайных величин. Причиной распространенности нормального распределения в прикладных науках, в том числе в педагогике, является общепринятое предположение о многочисленности и независимости факторов, влияющих на значение случайной величины — результата эксперимента, а также о том, что ни один фактор в отдельности не является определяющим.

Под выборкой будем понимать набор оценок, полученный в результате применения педагогического теста успешности обучения (или уровня формирования качества знаний, например, уровня информационной культуры личности [3] и т. п.) к группе объектов (школьников, студентов, слушателей). Предполагается, что с помощью применения различных методов шкалирования «оценка» обладает значительным числом фиксированных уровней, то есть представляет собой, по существу, количественную (интервальную) оценку, к которой могут быть применены любые математические процедуры.

Итак, в результате эксперимента получена выборка M (i = 1.....п) . Требуется проверить гипотезу Н , что эта выборка извлечена из некоторой нормально распределенной генеральной совокупности. Параметры этой совокупности обычно неизвестны и определяются по выборке

, где О=-У(х;-аУ — несмещенная вы-я—1 v 1      '

борочная оценка дисперсии.

Вычислим нормированные значения выборки:

• t, = (х^-а)/» .

По известным свойствам нормального распределения, если гипотеза Н верна, то (tj будет выборкой из стандартной нормальной генеральной совокупности с параметрами а = О, о = 1 .

Разобьем отрезок [О;1] на к (к = 2,3,...) одинаковых по длине промежутков и вычислим

_Zj = ф-^'/к), (j = 1,2,..., к- 1), где Ф^С/к) — обратная функция к функции стандартного нормального распределения.

Вычисление значений Zj упрощает номограмма, приведенная на рисунке 1. Достаточно нижнюю шкалу на номограмме разбить на k одинаковых частей, что легко сделать по специально нанесенным точкам разбиения в том случае, если k является делителем числа 24 (то есть k = 2, 3, 4, 6, 8, 12, 24). При этом на верхней шкале считываем значения z^ .

Тем самым мы получаем k непересекающих-ся промежутков: (-«-_fz3,(zv,zA...,(z_k-v,^ .

• ■             *                            X^J X .± Д. J ^г       \ И 1           jF

  

  Рис. 1. Номограмма для вычисления прямой и обратной функций распределения стандартного нормального распределения

  
  

Подсчитаем количество элементов tj выборки, попавших в каждый из этих интервалов. Пусть это будут числа и,- (/ = 1,2,...,к).

Очевидно, 2^_^Tiy = 71. Подсчитаем число к

Z2 =^У ^-^.       (1)

П £-^ 1

1=1

Это и есть величина /2 — мера отклонения экспериментального распределения выборки от стандартного нормального распределения.

Поясним этот факт преобразованием величины X² из работы [4, с. 454]:

„2 _ yk С^я7~^и^)^г

Z " ^=1 ^

HPj

^ V1 2

? 1               71 -       71 ■ ,

TiPj             71      *

где Ру — вероятность нормальной стандартной случайной величины попасть в j -й из указанных

1             ' V 1

промежутков, причем Pj = г для всех j и LPj = 1.

Как известно из работы [4, с. 457], если гипотеза H верна, то величина X должна быть мала, или она отличается от 0 только в силу случайных причин, точнее: большие отклонения X от 0 маловероятны. Это означает, что если величина X велика (произошло редкое событие), то гипотезу H следует отвергать. Однако следует понимать, что при этом мы можем допустить ошибку: отвергнуть все же верную гипотезу H !

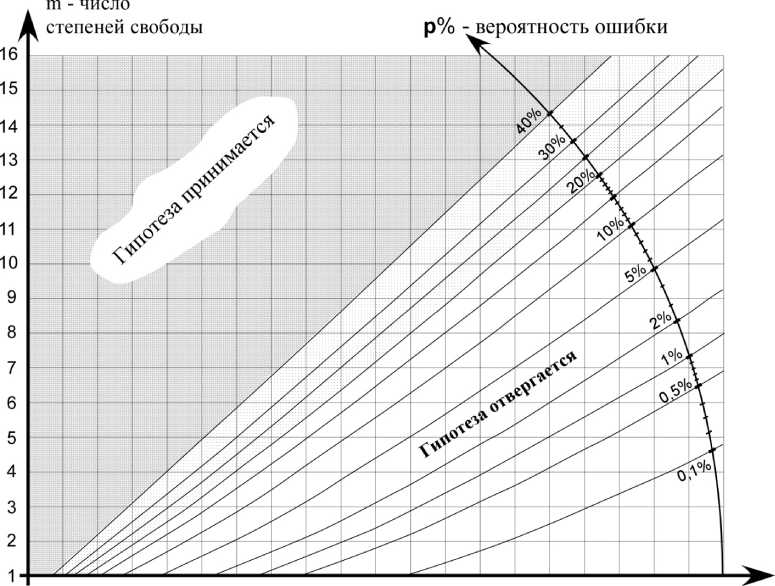
Вероятность этой ошибки p% , то есть вероятность отвергнуть верную гипотезу о принадлежности рассматриваемой выборки некоторой нормальной генеральной совокупности, может быть подсчитана с помощью специальной номограммы, приведенной на рисунке 2.

О 2       4       6       8      10      12      14      16     18      20       .

Значение %

Рис. 2. Номограмма для вычисления правосторонней функции X -распределения

Номограмма предназначена для решения уравнения

M>z²) = p%/100, где £ — случайная величина с X -распределением с т степенями свободы.

При использовании номограммы потребуется указать параметр т — число степеней свободы. В нашем случае он подсчитывается так: m = к — 3, если параметры нормального распределения оценивались по выборке, т = к — 1 — если параметры нормального распределения были заданы заранее. Кривые на рисунке 2 представляют собой линии одинаковой вероятности ошибки p% .

Для «вычисления» достаточно известные два числа из трех (х2 и m или p% и m) отло- жить на соответствующих шкалах номограммы; тогда на третьей шкале можно прочитать значение недостающей переменной.

Если полученная вероятность ошибки p% велика (например, более 40 %), то гипотезу H можно принимать, то есть признать нормальное распределение рассматриваемой выборки. Более осторожным (но и более надежным) является совет повторить эксперимент, получить новую выборку и еще раз проверить гипотезу.

Если эта вероятность мала (например, 5 % и меньше), то гипотезу о нормальности распределения выборки следует отвергать. В промежуточных случаях исследователь должен принимать решение, опираясь на свой опыт и уровень ответственности за то или иное принятое решение.

Можно следовать рекомендациям справочников по статистической обработке данных: заранее задаться уровнем значимости p% (обычно p = 0,1; 1 или 5 %); зная число степеней свободы m, вычислить по номограмме значение X ^1фИТ (оно называется критическим p -процентным уровнем значимости). Теперь, если вновь вычисленное по выборке значение X ^ ЛГкрит, то наша выборка обнаруживает значимое отклонение от гипотезы H (то есть экспериментальное распределение значимо отличается от нормального распределения), и мы должны гипотезу H отвергать на p% -м уровне значимости. Вероятность того, что такое положение возникнет в случае, когда гипотеза на самом деле справедлива и, следовательно, была отвергнута ошибочно, равна p% . Если вычисленное значение X — Лаурит, то это значение можно считать совместимым с гипотезой H .

Для проведения этапа планирования педагогического эксперимента следует отметить, что чем больше число степеней свободы (то есть число к – количество интервалов разбиения), тем надежнее будут результаты. Однако при этом должно быть выполнено условие, чтобы все п, >10[4, с. 457].

В качестве примера математического моделирования нами было сгенерировано по алгоритму Марсалье [7, с. 465] 1000 выборок по 1000 значений в каждой, выбранных из генеральной совокупности со стандартным нормальным распределением. Подсчитывая для каждой выборки величину X по описанной выше методике (для к = 12, т = 11), получили, что гипотеза о нормальности распределения выборки отвергается на 0,1 %-м уровне значимости ( X ^ Л^крит 31,3) всего 1 раз, на 1 %-м уровне значимости ( X. ^ 24,7) — 7 раз, на 5 %-м уровне значимости (/^ ^ ЛГмрит 19,6) — 46 раз. Эти данные укладываются в расчетные величины для х^г -распределения, что подтверждает как справедливость предлагаемой методики, так и хорошие качества использованного алгоритма генерации.

Отметим, что формула (1) подсчета величины X остается справедливой и для любого другого теоретического распределения генеральной совокупности. Например, для ло- гарифмически-нормального распределения набор промежутков (^-i? ^-] , 0 = 1,2,....^, вычисляется аналогично, но перед вычислением H; значения выборки X1 следует прологарифмировать по любому основанию. Для равномерного распределения на отрезке [a; b] достаточно этот отрезок разделить на /f одинаковых частей — это и будут точки zi . Расчеты по номограмме на рисунке 2 сохраняют свой смысл, только следует учитывать, что величина X будет иметь необходимое распределение только в асимптотическом смысле (при П -» co) .

Часто при статистической обработке педагогических данных возникает необходимость проверки гипотезы о независимости двух выборок. Например, в ходе тестирования слушателей с целью оценки успешности обучения фиксировался возраст слушателя. Вопрос: возраст и оценка коррелируют друг с другом или нет?

Рассмотрим гипотезу о независимости двух случайных величин X и Y , представленных своими выборками (^xi) и b'J. Подсчитаем выборочную ковариацию

(x, - х)(у6 - y) = - > Xjy, - xy

1 v cokZ—1

1=1 1 = 1

и вычислим выборочный коэффициент корреляции Пирсона cov(X,Y} r =----------,

Он характеризует характер и силу линейной зависимости случайных величин между собой. Всегда выполнено неравенство -1 < r < 1. Для независимых величин . Если верна гипотеза о независимости случайных величин, то значение r должно быть близко к нулю, то есть отклонение от 0 вызвано случайными, незначащими причинами. Оказывается [4, с. 438], в этом случае величина t = Vn- 2r/-Vl-r² имеет известное распределение Стьюдента с (n — 2 ) степенями свободы. Этот факт можно использовать для оценки вероятности ошибиться, отвергнув истинную гипотезу о независимости.

Подсчитаем в (2) числовое значение абсолютной величины коэффициента корреляции Пирсона |r| для данной выборки. Под- считаем по номограмме на рисунке 3 величину p%. Для этого достаточно обычной линейкой соединить две точки на соответствующих шкалах и на третьей шкале прочитать ответ. Это и будет вероятность ошибки, то есть вероятность отвергнуть верную гипотезу о независимости X и Y.

Если эта вероятность велика (например, более 40 %), то гипотезу о независимости следует принимать, то есть признать статистическую независимость этих случайных величин. Если эта вероятность мала (например, 5 % и меньше), то гипотезу о независимости следует отвергать, то есть признать статистическую зависимость этих случайных величин. В промежуточных случаях исследователь должен сделать вывод, опираясь на свой опыт и уровень ответственности за свое решение.

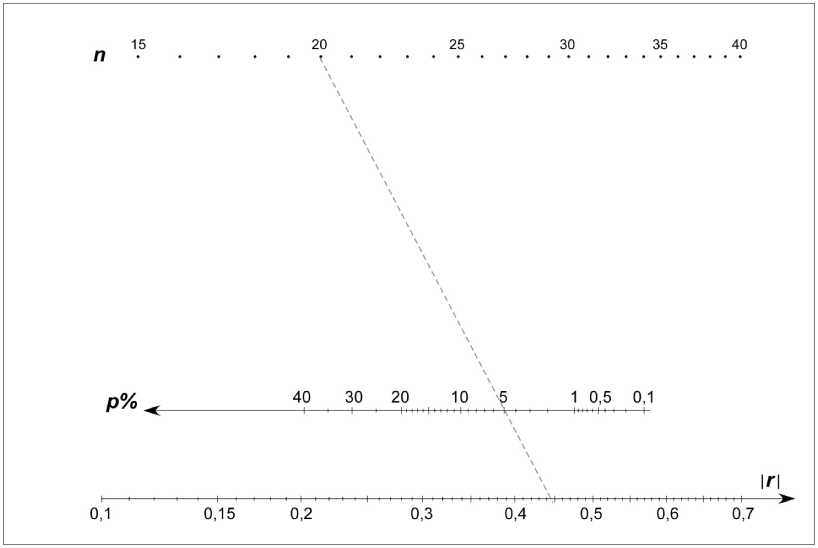
Рис. 3. Номограмма из выравненных точек для распределения Стьюдента (здесь n — количество элементов выборки; p% — вероятность допустить ошибку, отвергнув верную гипотезу о независимости; т — выборочный коэффициент корреляции Пирсона)

Можно поступить иначе: задаться заранее доверительной вероятностью p% (например, р = 10 %) и увеличивать п (если это возможно на стадии планирования эксперимента) или уменьшать 71 (может быть, за счет отбрасывания недостоверных результатов эксперимента), пересчитывая каждый раз по новой выборке коэффициент корреляции Г. Если при этом удается добиться, чтобы стало И > 6 (критическое значение 3 находится по номограмме на шкале |г| ), то гипотезу о независимости X и Y можно отвергать. При этом вероятность ошибиться в случае, если гипотеза все же верна, будет не больше p% .

В педагогических экспериментах часто ставится задача статистически проверить влияние или эффективность того или иного педагогического воздействия (новой методики, формы, средства, приема и т. п.). В этом случае формируются две группы испытуемых: группа 1 из испытуемых, подвергнутых изучаемому воздействию, и так называемая «контрольная группа 2», оставшаяся без указанного воздействия. В обеих группах отслеживается одинаковый признак, например, достигнутый уровень информационной культуры личности (или просто успеваемость по рассматриваемому предмету). Признак квантуется на к уровней, которые могут быть выражены как в порядковой, так и в номинальной шкале.

По окончании эксперимента составляется таблица («таблица сопряженности») количества обучающихся в каждой группе, находящихся на каждом из уровней успеваемости (табл. 1).

Таблица 1

Сопряженность признаков

Успеваемость	Группа 1	Группа 2	Всего	Доли
Уровень 1	31	hl	Si + hl	tii
Уровень 2	9г	^2	9: — ^2	ti2
		…
Уровень k	9k		9 k + ^k
Всего	m	n	m+n
			z2 =

Здесь ^i = 9iK9t + М, to = m/(m + n).

Величину z теперь можно вычислить по формуле, удобной для практических расчетов [4, с. 485]:

1 л

£U ( 1 — co)                      .

Вычислив в (3) по данным проведенного эксперимента величину z и сравнивая ее с ZspHT , вычисленной по номограмме на рисунке 2 при m = k – 1 степенях свободы, принимаем решение о значимости изучаемого педагогического воздействия: если Z -^ Zkpht , то гипотезу об однородности групп следует отвергать, и при этом вероятность ошибиться в случае, если гипотеза все же верна, будет не больше p% . В противном случае гипотезу об однородности групп по данному признаку можно принимать, что трактуется как отсутствие значимого влияния педагогического воздействия. Наоборот, неоднородность распределений трактуется как значимость исследуемого педагогического воздействия. Величину p% заранее берут малым числом (обычно 1, 5 или 10 %).

Статистическое обоснование данной процедуры следующее: число z является случайной величиной (так как зависит от случайной выборки), причем асимптотическое распределение этой величины известно. Если верна гипотеза об однородности двух выборок (то есть они извлечены из одной и той же генеральной совокупности), то значение / должно быть близко к нулю, и можно считать, что отклонение z от 0 вызвано случайными, незначащими причинами, причем вероятность этого отклонения может быть подсчитана.

• 1.    Жаркова, Г. А. Использование вычислительных номограмм при обработке данных педагогических экспериментов / Г. А. Жаркова // Сибирский педагогический журн. 2012. № 3. С. 13—19.

• 2.    Аванесов, В. С. Педагогическое измерение латентных качеств / В. С. Аванесов // Педагогическая диагностика. 2003. № 4. С. 69—78.

• 3.    Жаркова, Г. А. Метрическая модель информационной культуры учащихся / Г. А. Жаркова // Сибирский педагогический журн. 2011. № 3. С. 84—92.

• 4.    Крамер, Г. Математические методы статистики / Г. Крамер. М. : Мир, 1975. 648 с.

• 5.    Хованский, Г. С. Номография и ее возможности / Г. С. Хованский. М. : Гл. ред. физ.-мат. лит-ры изд-ва «Наука», 1977.

• 6.    Гайдышев, И. Анализ и обработка данных : спец. справ. / И. Гайдышев. СПб. : Питер, 2001. 752 с.

• 7.    Каханер, Д. Численные методы и математическое обеспечение : пер. с англ. / Д. Каханер, К. Моулер, С. Нэш. М. : Мир, 1998. 575 с.