Статистический анализ рисков информационной безопасности в автоматизированных системах

Современные условия функционирования систем защиты информации предполагают чрезвычайно динамичное развитие и высокую скорость реакции на возникновение и изменение внешних угроз. Для выполнения данной задачи активно используются различные экспертные системы.

Перспективным механизмом для реализации таких систем нам представляется вероятностный анализ процессов, протекающих в автоматизированной системе. Некоторые возможные реализации вероятностных моделей изолированных автоматизированных систем, а также анализ марковских процессов в этих системах с помощью формирования графа спонтанных переходов и построения на основе них системы уравнений Колмогорова рассматривались в некоторых работах [1]. Перспективным в практическом смысле развитием этой идеи представляется более подробное рассмотрение автоматизированной системы с описанием ее составных частей и влияния выхода из строя одних из них на надежность функционирования других и системы в целом, а также рассмотрением самого процесса реализации атаки на автоматизированную систему. Рассмотрение состава современных систем защиты информации не является предметом данной статьи, поэтому в рамках данной работы будем считать, что система защиты информации состоит из трех простых элементов (для примера рассматривается система из антивирусной системы, межсетевого экрана и системы шифрования критических данных). На этапе разработки модели такой подход позволит упростить теоретические выкладки без ограничения общности решаемой задачи. Добавление или исключение элементов системы защиты информации может производиться итеративно, тем же способом, что построение описываемой системы.

Процесс развития атаки на автоматизированную систему можно представить в виде трехдольного графа (рис. 1).

Рис. 1. Процесс развития атаки на автоматизированную систему.

Таким образом, автоматизированная система обладает набором полезных ресурсов, используемых в ходе ее функционирования. Система защиты информации обладает набором возможных уязвимостей, через которые реализуются некоторые возможные угрозы. Задача злоумышленника, осуществляющего атаку – обнаружить и реализовать угрозу через доступную уязвимость и, в результате, повредить или захватить какие-либо ресурсы автоматизированной системы, тем самым нарушив ее функционирование.

Серьезной проблемой применяемых на практике статистических моделей является необходимость набора статистики функционирования системы. Чем больше и полнее накопленный объем статистических данных, тем точнее может быть дан прогноз.

Типичными условиями применения экспертных систем на основе вероятностного анализа процессов можно считать их применение к уже функционирующей системе, статистика по которой, как правило, ограничивается логами систем защиты информации и журналом инцидентов. Экспертные методы позволяют частично исключить присутствующие в данных источниках ошибки первого и второго рода и получить пригодные для первичной оценки данные. Точность таких методов, ввиду субъективности, невелика, однако она может быть несколько повышена при декомпозиции и, следовательно, упрощении задачи. При построении нашей модели мы ограничимся частью графа, приведенного на рис. 1, приходящей к единственному ресурсу автоматизированной системы. Такое выделение элементов позволит проанализировать вероятность выхода из строя одного из ресурсов автоматизированной системы, при этом общность решаемой системы не нарушается: для остальных ресурсов анализ может быть повторен.

Прямое описание угроз и уязвимостей реальной системы чрезвычайно сложно реализовать, поскольку их статистику, как правило, значительно сложнее восстановить, чем статистику инцидентов. В связи с этим мы не будем производить попыток формализовать угрозы и уязвимости для анализируемой системы в общем виде, ограничившись описанием состояний, вызванных нарушением работоспособности элементов системы защиты информации или их группы. Такой подход позволит максимально упростить восстановление статистики и интерпретацию результатов для реальной системы, сохраняя возможность анализа сложных систем и многоступенчатых атак.

Система, используемая в нашей модели, будет состоять из трех базовых состояний: S 0 – работа системы в нормальном режиме, S 1 – система атакована, S 2 – работоспособность системы нарушена, исследованный ресурс поврежден или захвачен. Кроме того, в системе присутствуют до

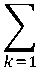
№ k\(N -к)\

состояний нарушенной работоспособности [2], где N – число рассматриваемых элементов системы защиты. Для нашего слу- чая (3 элемента) таких состояний может быть до семи, обозначим их Sнi,…l, где индексами обозначены антивирусная система (индекс 1), межсетевой экран (индекс 2) и система шифрования (индекс 3) критических данных. В данных состояниях часть элементов системы (с номерами, соответствующими индексам i,…l) защиты неработоспособна или захвачена.

При таком подходе атака развивается следующим образом: злоумышленник атакует нормально функционирующую систему, и она переходит в атакованное состояние, результатом атаки может быть нарушение функционирования системы, то есть повреждение выбранного ресурса или нарушение работоспособности одного или нескольких элементов системы защиты информации, через которые уже осуществляется дальнейшее развитие атаки (многоступенчатая атака).

Для рассматриваемой системы возможны переходы из S 1 в S н1 , S н2 , S н3 и S н12 , из S н1 в S н12 и S 1 , из S н2 в S н12 и S 1 и сложное состояние S н12 . Граф состояний такой системы приведен на рис. 2.

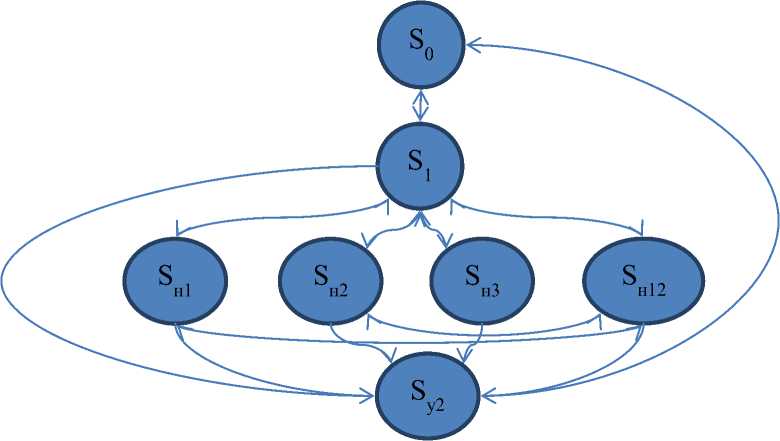
Рис. 2. Граф состояний реальной системы.

Уравнения Колмогорова [3] для данной системы примут следующий вид (4):

Pq = ^l;0 ‘ Pl to + ^y2;0 ' Py2 to — ^0;l ' Poto(2.1)

Pl = ^0;l " Poto + ^Hl;l " PHlto + ^н2;1 ' Ph2 to + ^нЗ;1 ’ Рнз(0 + ^н12;1 ' Рн12(0(2.2)

• - (Л1;0 + ^1;н1 + ^1;н2 + ^1;нЗ + ^1;н12 + ^1;у2) ’ ^Plto

Рн1 = ^н12;и1 ' Ри12(0 + ^1;и1 * Plto — (^н1;н2 + ^н1;н12 + ^н1;у1) ’ Рн1(0(2.3)

Рн2 = ^н12;и2 ' Рн1г(0 + ^1;н2 ' P1W — (^н2;н1 + ^-н2;н12 + ^н2;1) ’ Рн2 W(2.4)

РнЗ ~ ^1;иЗ " Р1(0 — (^нЗ;1 + ^нЗ;у2) ' РнЗ (О(2.5)

Рн12 = ^н1;и12 ' Ри1(0 + ^н2;и12 ' Р»г(С — С^н12;н1 + ^-н12;н2 + ^н12;1 + ^-н12;у2)(2.6)

' Pnl2(t)

Ру2 = ^1;у2 - P«l(t) + ^,2;у2 ‘ В/гСО + ^нЗ;у2 ’ Р»3 to + ^н12;у2 ' PW12to + ^1;у2 ' Р1(0(2.7)

• — Ху2;0 " Ру2 to

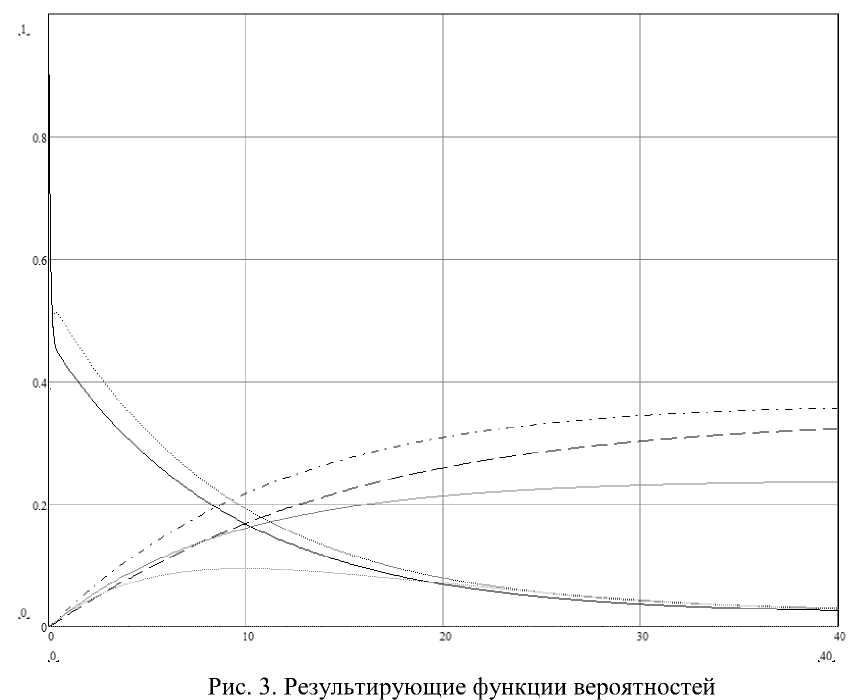
Для характерных для практических систем чисел результирующие функции могут иметь такой вид (см. рис.3).

На графике рис. 3 по оси абсцисс отложено время, по оси ординат – вероятности, линиями обозначены: сплошная черная – S0, точечная черная – S1, точка-пунктирная черная – Sн1, пунктирная черная – Sн2, сплошная серая – Sн3, пунктирная серая – Sн12, точка-пунктирная серая – Sу2. Полученные кривые наглядно демонстрируют процессы, которые будут протекать в системе. После приблизительно двух недель ее работы вероятности падения антиви- русной системы или межсетевого экрана весьма велики, вероятность падения их обеих или системы шифрования – значительно меньше. Вероятность повреждения исследуемого ресурса имеет пик в районе десятого дня, но, в целом, имеет небольшую величину.

Таким образом, такой подход позволяет численно охарактеризовать устойчивость автоматизированной системы и системы защиты в ее составе поэлементно на основе статистических данных о них, не прибегая к чрезмерно сложным вычислениям.