Статистический эксперимент на имитационной модели уборочно-транспортного комплекса и его результаты

Автор: Николаев Николай Николаевич

Журнал: Вестник аграрной науки Дона @don-agrarian-science

Рубрика: Механизация и электрификация животноводства, растениеводства

Статья в выпуске: 1 (17), 2012 года.

Бесплатный доступ

Представлена методика проведения статистических экспериментов с применением методов имитационного моделирования. Имитационное моделирование позволяет исследовать работу уборочно-транспортного комплекса на уборке зерновых колосовых культур с различными параметрами, которые изменять в полевых условиях не представляется возможным. При планировании эксперимента и обработке экспериментальных данных использовались современные компьютерные технологии.

Имитационная модель, уборочно-транспортный комплекс, статистический эксперимент, матрица, план, факторы, параметр, оптимизация, адекватность, дисперсия, поверхность, отклик, регрессия

Короткий адрес: https://sciup.org/140204138

IDR: 140204138

Текст научной статьи Статистический эксперимент на имитационной модели уборочно-транспортного комплекса и его результаты

При проектировании процессов и технических средств необходимо уметь определять номинальные параметры машин, оптимальные режимы работы линий, которые зависят от соотношения параметров взаимодействующих машин, их компоновки, конструктивно-технологических характеристик, способов компенсации несовпадения циклов.

Существуют два основных подхода к моделированию, учитывающих случайную природу процессов. Это аналитические и статистические методы моделирования. К аналитическим методам относится теория массового обслуживания. Эти методы обладают известными недостатками [1]. К статистическим методам относится метод имитационного моделирования. Сущ-26

ность метода состоит в следующем. При проведении полевых испытаний или наблюдений за работой в условиях сельхозпредприятия проводится хронометраж всех ключевых элементов процесса. Затем проводится статистическая обработка полученных выборок случайных величин с целью определения законов их распределения. Далее, при разработке модели на ПК случайные элементы процесса моделируются как случайные величины, распределенные по полученным законам, путем преобразования по соответствующим алгоритмам закона равномерной плоскости либо используются функции, включенные в системы математического моделирования.

Нами совместно с И.Н. Черноусовым разработана «Имитационная модель функционирования уборочно-транспортного комплекса на уборке зерновых колосовых культур с использованием системы оперативного управления», которая зарегистрирована в реестре программ для ЭВМ Российской Федерации [2].

Данная модель позволяет воспроизводить работу двух уборочно-транспортных групп на уборке зерновых колосовых культур с высокой степенью детализации. При этом можно рассмотреть шесть режимов работы (с бункером-накопителем и без него, при наличии оперативного управления и его отсутствии, а также с возможностью вызова резерва транспорта и без резерва). На этой модели можно производить разнообразные исследования с целью определения оптимальных параметров уборочно-транспортных комплексов и границ рационального использования той или иной технологии.

В данной статье рассмотрена методика статистического эксперимента с использованием программы STATISTICA 6.

Для создания плана эксперимента и его последующей обработки используется модуль Experimental Design (Планирование эксперимента). На стартовой панели модуля необходимо выбрать тип плана эксперимента (рис. 1) с учетом его целей.

Quick Advanced

! ^_r 2"4K p) standard designs (Box. Huntes, t Huntes)

^c 2-level screening |PlacketiBurman| designs

^r 2“(Kp) max unconlounded or min aberration designs

For Mfaaorul designs. hierarchicily nested models« des»flhs with unbatoneed nenng. wsd mixedmodrt (гамет etfeot) designs, see *0 \*іжке Comoowes andGUd

^^ 3”|Kp) and Box-Behr* en designs

^t Mixed 2 and 3 level designs

1^ Central composite, nonlactoual. surface designs

;|Ц Latin squares. Greco Latin squares

Taguchi robust design experiments (orthogonal arrays) ^ Mixture designs and triangular surfaces [pi] Designs for constrained surfaces and mixtures [d] 0- and A- (T ■) optimal algorithmic designs

(^ Open Bata I

«sis 1 I О Й I

Рис. 1. Стартовая панель модуля «Планирование эксперимента»

Затем необходимо выбрать наиболее рациональный план эксперимента с учетом числа факторов.

Для целей нашего исследования подходят трехуровневые планы (рис. 2).

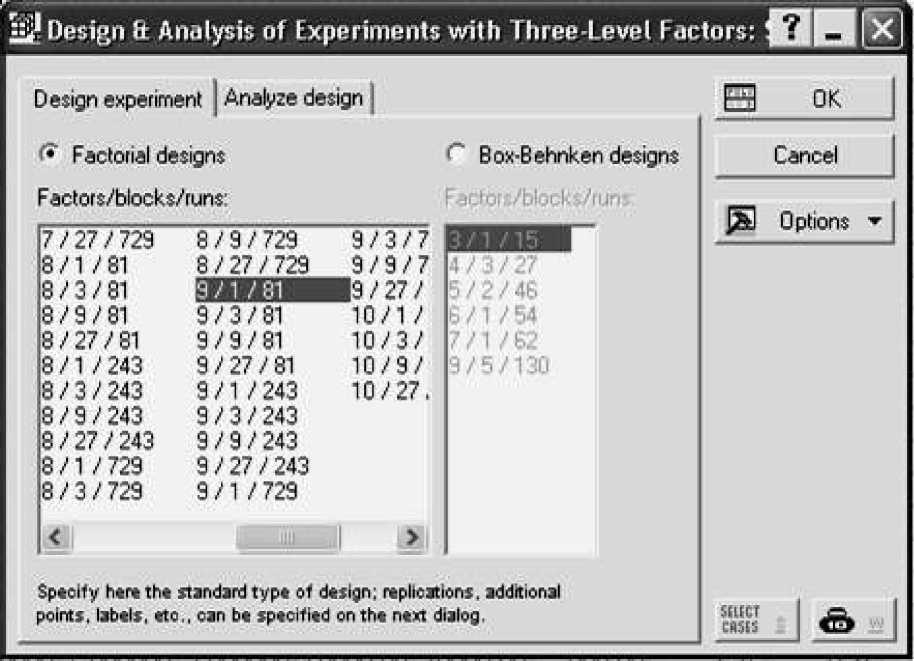
Рис. 2. Трёхуровневые планы

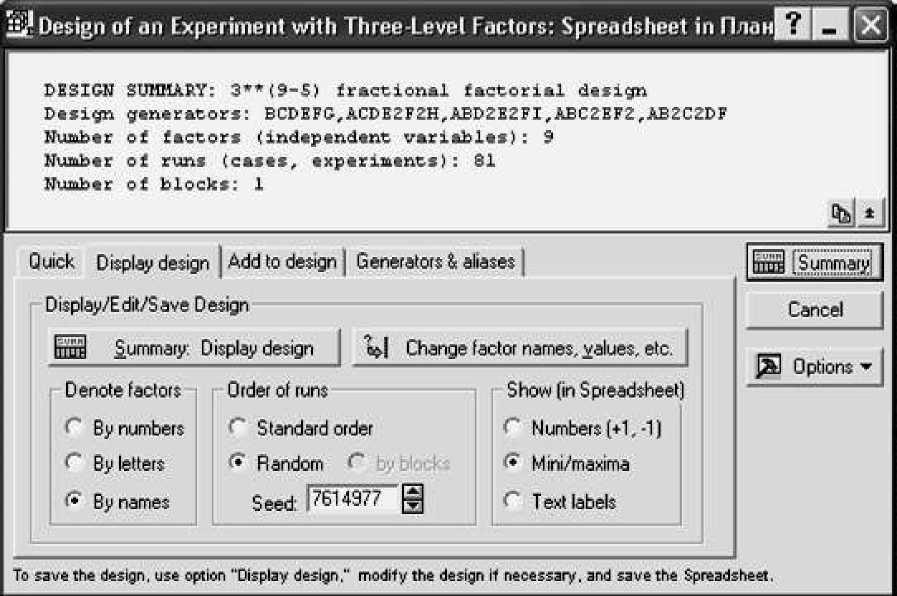
Рис. 3. Параметры плана эксперимента

Поле этого в открывшемся окне необходимо задать параметры выбранного плана (порядок проведения опытов, количество параметров оптимизации, количество опытов в центре плана и другие) (рис. 3).

В результате нами получен трехуровневый девятифакторный план эксперимента с дробной репликой дробностью 5. Для его реализации необходимо провести 81 опыт (рис. 4).

3**(9-5) fractional factorial design, 1 block ,81 runs (Spreadsheet in Workbook!)

Standard Run	n1	mt	Һ2 m2	Up1	Up2 L1 12	Lgroup W1	W2	W
2	1 ,□□0000	1,00000	1,000000 10,00000	6,000000	6,000000 10500,00 1000,00	5250,00 4,54	11.03	15,57
47 17	3.000000 1.000000	19,00000 10,00000	1,000000 10,00000 5,000000 10,00000	2,000000 2,000000	2,000000 1000,00 10500,00 6,000000 1000,00 20000,00	5250,00 2.44 5250,00 3,84	2,46 11,97	4,90 15.81
62	5,000000	1,00000	5,000000 10,00000	6,000000	6,000000 20000,00 20000,00	10000,00 2,67	10,50	13,16
29	3,000000	1,00000	1,000000 10,00000	2,000000	4,000000 10500,00 20000,00	10000,00 2,68	3,51	6,39
44	3,000000	10,00000	5,000000 10,00000	4,000000	4,000000 1000,00 10500,00	10000,00 9,23	12,40	21,63
25	1,000000	19,00000	5,000000 1,00000	4,000000	4,000000 1000.00 1000,00	5250,00 15,55	13,50	29,05
4	1,000000	1,00000	3,000000 1,00000	6,000000	4,000000 20000,00 20000,00	5250,00 2.16	2,38	4,54
28	3,000000	1,00000	1,000000 1,00000	4,000000	6,000000 1000,00 20000,00	5250,00 12,48	2.22	14,69
50	3,000000	19,00000	3,000000 10,00000	6,000000	4,000000 20000,00 1000,00	10000,00 4,50	8.89	13.40
13	1,000000	10,00000	3,000000 1,00000	6,000000	6,000000 1000,00 1000,00	10000,00 13,88	5,96	19,83
69 60	5,000000 5,000000	10,00000 1,00000	3,000000 19,00000 3,000000 19,00000	6,000000 6,000000	4,000000 20000.00 10500,00 2,000000 10500,00 1000,00	500,00 12.51 10000,00 4,50	3,52 14.42	16.04 18,92
57	5,000000	1,00000	1,000000 19,00000	2,000000	6,000000 20000,00 10500,00	5250,00 1,86	4,16	6,01
27	1,000000	19,00000	5,000000 19,00000	6,000000	6,000000 20000,00 1000,00	500,00 5,69	26,11	31,80
53	3,000000	19,00000	5,000000 10,00000	4,000000	6,000000 10500,00 20000,00	500,00 5,01	16,65	21,66
74	5,000000	19,00000	1,000000 10,00000	4,000000	6,000000 1000,00 1000,00	10000,00 14,57	12,55	27,13
40	3,000000	10,00000	3,000000 1,00000	2,000000	4,000000 1000,00 20000,00	500,00 9,08	2,65	11.74
30	3,000000	1,00000	1,000000 19,00000	6,000000	2,000000 20000,00 20000,00	500,00 2,62	2,88	5,50
79	5,000000	19,00000	5,000000 1,00000	2,000000	6,000000 1000,00 10500,00	500,00 17,34	3.90	21,23
58	5,000000	1.00000	3,000000 1.00000	4,000000	5,000000 20000,00 1000,00	500,00 4.73	8.23	12.96
5	1 .oooooo	1,00000	3,000000 10,00000	4,000000	2,000000 1000,00 20000,00	10000,00 3,97	5,50	9,47
63	5,000000	1,00000	5,000000 19,00000	4,000000	4,000000 1000,00 20000,00	500,00 7.10	20,72	27,81
61	5,000000	1,00000	5,000000 1,00000	2,000000	2,000000 10500,00 20000,00	5250,00 4,51	3.92	8,43

Рис. 4. План эксперимента (фрагмент)

В плане эксперимента факторами являются (слева направо): количество комбайнов и автомобилей в первой и второй уборочно-транспортной группах, урожайность на полях, убираемых первой и второй группами, расстояние от них до тока, расстояние между этими полями. В качестве параметров оптимизации выбраны: производительность первой и второй группы и комплекса в целом.

В имитационной модели предусмотрено получение результатов по нескольким заданным сменам работы, что позволяет сбалансировать воздействие случайных факторов.

После получения параметров оптимизации необходимо произвести обработку плана эксперимента с целью анализа влияния различных факторов на параметры оптимизации и получение коэффициентов уравнения регрессии. Для этого выбираются параметры оптимизации и факторы, относительно которых будет проводиться анализ (рис. 5).

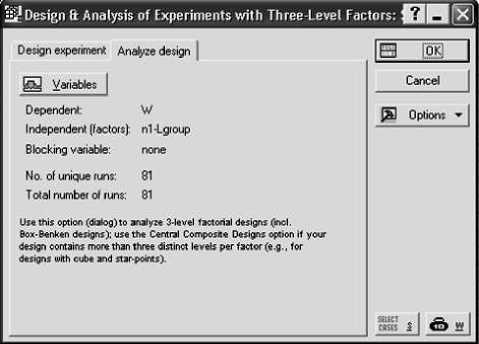
Рис. 5. Выбор параметров анализа плана эксперимента

При анализе можно получить коэффициенты уравнения регрессии в кодированном виде, оценить эффекты факторов, выявить значимые составляющие уравне- ния, а также оценить адекватность аппроксимации через коэффициент детерминации и скорректированный коэффициент детерминации (рис. 6).

Effect Estimates; Var.:W; R-sqr= ,75721; Adj: ,68672 (Spreadsheet in План экспериментаЗв(9-5)с yn без;

9 3-level factors, 1 Blocks, 81 Runs; MS Residual=23,11687

DV; W

Factor	Effect	Std.Err.	t(62)	P	-95,% Cnf.Limt	495,% Cnf.Limt	Coeff.	Std.Err. Coeff.	-95,% Cnf.Limt	+95,% Cnf.Limt
Mean/lnterc.	13,852051	0,534222	25,92937	0,000000	12,7842	14,91994	13,85205	0,534222	12,78415	14,91994
0)n1 (L)	4,40818	1,308572	3,36869	0,001303	1,7924	7,02397	2,20409	0,654286	0,89619	3,51199
nt (Q)	-1,65447	1,133257	-1,45993	0,149358	-3,9198	0,61087	-0,82724	0,566628	-1,95991	0,30544
(2)m1 (L)	4,45673	1,308572	3,40580	0,001162	1,8409	7,07253	2,22837	0,654286	0,92047	3,53626
mt (Q)	2,14884	1,133257	1,89617	0,062600	-0,1165	4,41419	1.07442	0,566628	-0,05825	2,20710
C3)n2 (L)	6,50495	1,308572	4,97103	0,000006	3,8892	9,12075	3,25248	0,654286	1,94458	4,56038
n2 (0)	-0,63905	1,133257	-0,56391	0,574850	-2,9044	1,62629	-0,31953	0,566628	-1,45220	0,81315
(4)m2 (L)	0,67072	1.308572	0,51256	0,610080	-1,9451	3,28652	0,33536	0,654286	-0,97254	1,64326
m2 (Q)	1,68718	1,133257	1,48879	0,141611	-0,5782	3,95253	0,84359	0,566628	-0,28908	1,97627
(5)Up1 (L)	10,00977	1,308572	7,64939	0,000000	7,3940	12,62557	5,00489	0,654286	3,69699	6,31279
Up1 (Q)	0,27956	1,133257	0,24669	0,805964	-1,9858	2,54491	0,13978	0,566628	-0,99289	1,27246
(6)Up2 (L)	4,86126	1,308572	3,71493	0,000438	2,2455	7,47705	2,43063	0,654286	1,12273	3,73853
Up2 (Q)	0,66595	1,133257	0,58764	0,558908	-1,5994	2,93130	0,33297	0,566628	-0,79970	1,46565
(7)L1 (L)	-9,45746	1,308572	-7,22731	0,000000	-12,0733	-6,84166	-4,72873	0,654286	-6,03663	-3,42083
L1 (Q)	-0,44565	1,133257	-0,39325	0,695486	-2,7110	1,81970	-0,22283	0,566628	-1,35550	0,90985
(8)12 (L)	-2,69149	1,308572	-2,05681	0,043918	-5,3073	-0,07569	-1.34574	0,654286	-2,65364	-0,03784
12 (Q)	-2,53634	1,133257	-2,23810	0,028816	-4,8017	-0,27099	-1,26817	0,566628	-2,40084	-0,13550
O)Lqroup (L)	-1,76681	1,308572	-1,35018	0,181867	-4,3826	0,84899	-0,88340	0,654286	-2,19130	0,42450
Lgroup (Q)	1,13742	1,133257	1,00367	0,319438	-1,1279	3,40277	0,56871	0,566628	-0,56396	1,70138

Рис. 6. Оценки эффектов факторов

При этом установлено, что коэффициент детерминации равен 0,75, а скорректированный коэффициент детерминации равен 0,69, то есть качество аппроксима- ции достаточно высокое.

Также можно получить коэффициенты уравнения регрессии в раскодированном виде (рис. 7).

Regr Coefficients; Var,:W; R-sqr= ,75721. Adj: .68672 (Spreadshei 9 3-level factors. 1 Blocks. 81 Runs; MS Residual=23,11687 DV: W

Factor	Regressn Coeff.	StdErr	t(62)	P	-95.% Cnf Limt	♦95.% Cnf Limt
Mean/lnterc.	-5.03726	6,727246	•0,74879	0,456818	-18,4848	8,410309
(1)n1 (L)	-1.37967	1.731078	•0,79700	0,428493	•4.8400	2,080709
nt (Q)	0,41362	0,283314	1.45993	0,149358	•0,1527	0.979955
0m1 (L)	0,77818	0,289106	2,69166	0,009128	0,2003	1,356090
ml (Q)	-0,02653	0,013991	-1,89617	0,062600	-0.0545	0.001438
S)n2 Д.1_	0,66766	1.731078	0,38569	0,701047	-2,7927	4,128034
n2 (Q)	0,15976	0,283314	0,56391	0,574850	-0.4066	0,726100
(4) m2 (L)	0,45385	0,289106	1.56984	0,121542	-0.1241	1,031766
m2 (Q)	-0,02083	0,013991	-1.48879	0,141611	-0,0488	0,007138
(5)U p1 (L)	3,06157	2,290001	1,33693	0,186131	-1,5161	7,639215
Up1 (Q)	-0,06989	0,283314	•0,24669	0,805964	■0.6362	0.496446
№2 JL^ Up2 (Q)	2,54721 -0,16649	2,290001 0,283314	1,11232 •0,58764	0,270296 0,558908	-2.0304 •0,7328	7,124856 0,399850
QL1 (L)	-0,00060	0,000273	-2,20686	0,031035	-0.0011	■0.000057
И (Q) № (L)	0,00000 -0,00073	0,000000 0,000273	0,39325 -2,68522	0,695486 0,009287	■0,0000 -0,0013	0,000000 -0,000187
L2 (Q)	0,00000 0.000000		2,23810	0,028816	0.0000	0,000000
(9)Lgroup (L)	0,00034	0,000545	0,62990	0,531075	-0.0007	0,001433
Lgroup (Q)	-0,00000	0,000000	-1.00367	0,319438	-0.0000	0.000000

Рис. 7. Коэффициенты уравнения регрессии

После этого могут быть получены различные поверхности отклика (рис. 8).

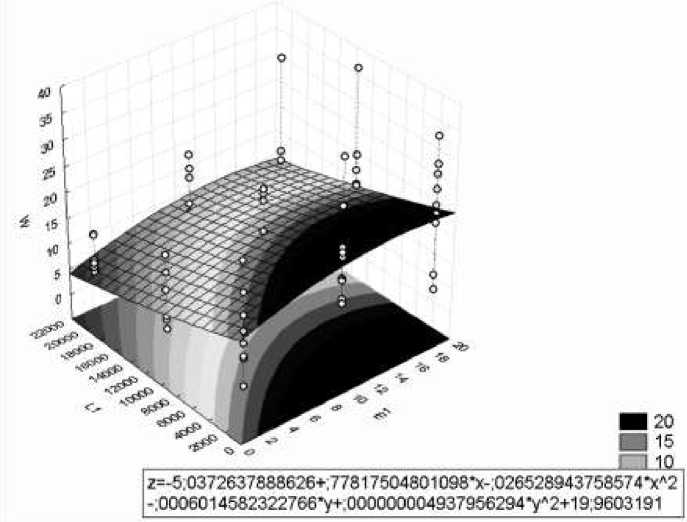
і t6

Z=-5;0372637888626*.77817504801098*X-:026528943758574*xA2

-000601458232276буһ000000004937956294-уА2+19;9603191

Рис. 8. Поверхность отклика

При этом выводится уравнение, описывающие данную поверхность отклика, отражающую зависимость параметра оптимизации от двух выбранных переменных факторов при фиксации остальных на определенных исследователем уровнях.

В процессе статистических экспериментов получены коэффициенты уравнений регрессии как в кодированном, так и в раскодированном виде. Уравнения описывают исследуемый процесс и образуют математическую модель, позволяющую определить оптимальные параметры системы для заданных условий её работы.

Статья научная