Статистический метод исследования эстетических предпочтений российской и западной киноаудиторий

аждую неделю в российский кинопрокат выходит несколько фильмов. Например, в 2008 г. по данным сайта в прокат вышли 339 кинофильмов.

Используя Интернет, можно узнать самые различные сведения об этих фильмах: просмотреть трейлер, галерею, составленную из отдельных кадров, прочитать аннотацию, рецензии профессиональных и непрофессиональных рецензентов.

В настоящее время можно говорить о существовании массового интернет-сообщества, охватывающего широкие круги любителей кино (синефилов), которые участвуют в постоянно проводимых опросах на сайтах для киноманов. На этих сайтах автоматически обобщаются статистические характеристики выражения мнений.

БОЯРШИНОВА Елена

ГААХ

Непосредственно мнение синефилов по отношению к каждому фильму выражается в виде оценки по десятибалльной шкале в индексах Top250 и IMDB . Индекс Top250 используется русскоязычной публикой, а индекс IMDB является интернациональным. Количество оценок фильмов, вышедших в мировой прокат, на сайте IMDB в десятки раз больше, чем на сайте Top250 . Средние оценки фильмов, публикуемые этими индексами, могут служить для сравнения вкусов активных кинозрителей. Кроме непосредственных оценок, выраженных баллами, имеется показатель, характеризующий интерес синефилов, – это количество людей, поставивших свою оценку фильмам на сайтах Top250 и IMDB .

Статистическая сводка мнений профессиональных англоязычных кинокритиков (количество англоязычных рецензий и доля среди них положительных рецензий, а также средняя оценка фильмов рецензентами по десятибалльной шкале) доступна на сайте Кроме того, сборы фильмов в кинопрокате позволяют сравнивать интерес публики к различным фильмам. Сборы от проката в России и (отдельно) в США также доступны на этом сайте.

В данной статье используется информация обо всех указанных оценках по 142 из 339 фильмов, вышедших в российский кинопрокат в 2008 г.

Как правило, с помощью Тор250 составляется и постоянно корректируется список 250 самых лучших фильмов, в журналах со- ставляются десятки лучших фильмов. Мы предлагаем несколько иной инструмент, который позволяет выделять различия в оценке фильмов независимо от того, в какой части рейтингового списка они находятся.

Рассмотрим вопрос на языке математической статистики. О некотором количестве объектов (в нашем случае – фильмов) известны две количественные характеристики. В нашем случае их можно выбрать из широкого списка: оценка синефилов Top250 ; оценка синефилов IMDB ; количество людей, выразивших свое мнение в рейтинге Top250 ; количество людей, выразивших свое мнение в рейтинге IMDB ; сборы фильма в российском прокате; сборы фильма в прокате США; оценка, данная фильму англоязычными рецензентами; процент англоязычных рецензентов, положительно оценивших фильм; общее количество англоязычных рецензий; а также любые другие количественные характеристики зрительского внимания или зрительского восприятия, которые можно найти в Интернете.

Мы имеем дело с парой количественных характеристик для некоторого количества объектов (фильмов). Обозначим эти характеристики {x_i;y_i} . Индекс i – это порядковый номер, он меняется от 1 до n . Существует математический критерий – коэффициент корреляции, который позволяет оценить степень обоснованности применения линейной зависимости для описания связи между величинами y и x . Этим критерием является коэффициент линейной корреляции. Для его вычисления разумно использовать следующую формулу:

_ COV xy _ ( x • У ) - x • У r" D x       X 2 - ( X ) ^{2           .}

В этой формуле горизонтальные черточки над выражениями означают усреднение. В частности:

nnnn

____ 2 ( X i • y. )     2 X i _ 2 y. _ 2 x ² i

( x • y ) _ j_ 1--------- ; x _ ' ; y _ ' ; x² _ ^= 1 .

nnnn

Следует иметь в в иду, что x² * ( x ) . Величины      cov_xy = ( x • y ) - x • y        и

D _x = x ² - ( x ) называются в статистике соответственно ковариацией и дисперсией.

Коэффициент линейной корреляции изменяется в пределах от –1 до +1. Если коэффициент корреляции больше нуля, говорят о положительной корреляции. В этом случае большим значениям одной из переменных чаще соответствуют большие значения другой переменной. В случае отрицательной корреляции все наоборот: большим значениям одной из исследуемых величин соответствуют меньшие значения другой величины. Считается, что абсолютное значение коэффициента корреляции является мерой тесноты связи двух величин. Чем ближе к единице, тем теснее связь. Если коэффициент корреляции отличается от нуля менее чем на 0,2 … 0,3, то это указывает на отсутствие связи между величинами или ее крайне низкую степень.

Сама по себе величина коэффициента линейной корреляции говорит о многом. Например, по результатам проката 2008 г. коэффициент корреляции между оценкой синефилов Top250 и сборами проката отсутствует: коэффициент корреляции равен 0,047. Это очень важный результат. Сборы никак не связаны с художественным и эстетическим качествами фильмов. Зато количество людей, давших свою оценку фильмам, зависит от сборов очень заметно. Коэффициент корреляции количества оценок на Top250 и сборов в РФ составляет 0,635. Это достаточно ожидаемый результат – количество просмотревших фильм синефилов определяется интенсивностью его проката.

Еще теснее корреляция оценок Top250 и IMDB – для этой пары величин коэффициент корреляции равен 0,794; а количества проголосовавших коррелируют с коэффициентом 0,743. Значит, в целом оценка фильма и внимание к нему со стороны отечественных и зарубежных синефилов определяются эстетическими критериями.

Но наибольший интерес представляют различия. Повторяем, мы имеем дело с парой количественных характеристик для некоторого количества фильмов. Мы обозначили эти характеристики {x_i; y_i} , где индекс i – это порядковый номер, он меняется от 1 до n .

Если изобразить эти точки на координатной плоскости XOY, то они образуют в большей или меньшей степени вытянутое облачко. Сразу появляется желание изобразить зависимость между y и x с по- мощью прямой линии, то есть линейной функции:

y _i = kx_i + b .

Оправданность такого приближения тем выше, чем больше коэффициент линейной корреляции. Известен с эпохи Возрождения метод построения таких зависимостей. Он носит название метода наименьших квадратов. Этот метод заключается в подборе таких значений параметров зависимости (в нашем случае это k и b ), чтобы сумма квадратов отклонений теоретических значений от фактических была бы минимальной. Отклонение факт и ческого значения ( y_i ) от теоретического ( y _i ) выража е тся формулой

ε _i = y_i – y _i= y_i – kx_i –b .

Эта задача давно решена и имеет простое решение:

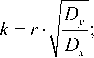
b = y - k • x .

Величина отклонения фактических значений от расчетных ( ε _i ) является мерой соответствия теоретической зависимости фактической для каждого конкретного случая. Среднее квадратичное отклонение фактических значений от теоретических (остаточная дисперсия) является мерой точности соответствия зависимости фактическому положению дел в целом. Производной от нее величиной является остаточное среднее квадратичное отклонение, обычно обозначаемое греческой буквой сигма ( ). Эти величины легко вычислить по формулам:

n

Z e 2

= -^1;^    =. D .

ост .          * ^;^ ост .    у    ост .

n - 2

Значение этих величин трудно переоценить. Напомним так называемое правило «трех сигм». Очень редко случайная величина отклоняется от своего среднего значения более чем на три средних квадратичных отклонения (три сигма).

Если такое отклонение происходит, то применительно к объекту можно утверждать, что объект является особенным. Проиллюстрируем вышесказанное примером.

Если в качестве пары величин ( y и x ), между которыми исследуется степень зависимости, использовать две величины:

количество любителей кино, давших свои оценки на Top250 , и сборы в РФ (коэффициент корреляции этих величин 0,635; количество фильмов, для которых имеются эти данные – 317), то выяснится интересный факт. Более чем на три сигма (или чуть меньше) превосходит ожидаемый со стороны синефилов интерес к следующим фильмам: «Сумерки» (8,5 ), «Темный рыцарь» (7,0 ), «ВАЛЛ-И» (5,8 ), «Я – легенда» (3,7 ), «Заложница» (3,3 ), «Железный человек» (2,6 ), «Суиннитод: демон-парикмахер с Флит-стрит» (2,6 ).

Ажиотажное внимание фильму «Сумерки» обеспечила аудитория, состоящая из молодых зрительниц. Понятно преувеличенное внимание к фильму «Темный рыцарь». В этом фильме сыграл свою последнюю роль трагически ушедший из жизни актер Хит Леджер. Остальные три фильма выделились благодаря своим художественным качествам и сниженному интересу к ним со стороны массового зрителя.

Несопоставимо мало внимания синефилы уделили следующим фильмам: «Мадагаскар-2» (–3,4 ), «Адмирал» (–2,6 ), «Мумия: Гробница Императора Драконов» (–2,6 ). Это отставание легко интерпретировать. Фильмы оказались востребованы аудиторией, состоящей из людей, не принадлежащих к интернет-сообществу. Фильмы «Мадагаскар-2» и «Мумия: Гробница Императора Драконов» были кассово успешны, но рассчитаны на детскую аудиторию. Фильм «Адмирал» не заслужил внимания у любителей кино по эстетическим причинам. Казалось, новый подход к изложению событий революции и гражданской войны не мог не привлечь внимание синефилов старших возрастов, однако последние редко высказывают свои взгляды через Интернет.

Для исследования зависимости между количеством любителей кино, давших свои оценки на Top250 , и сборами в РФ было использовано 317 фильмов. Примененный нами метод позволил выделить из этой массы 10 фильмов. Это менее 3%. Таким образом, использованный нами метод позволяет сконцентрировать внимание исследователей на фильмах, чья оценка различными киноаудиториями отличается в наибольшей степени, хотя эти фильмы могут находиться в общей рейтинговой массе.