Статистический учет многорежимности в задаче оптимальной компенсации реактивных нагрузок при построении интеллектуальных электроэнергетических систем

В настоящее время в Российской Федерации активно реализуется политика перехода к цифровой экономике. В 2019 г. Правительством Российской Федерации была разработана национальная программа «Цифровая экономика Российской Федерации», утвержденная протоколом заседания президиума Совета при Президенте Российской Федерации по стратегическому развитию и национальным проектам от 04.03.2019 № 7, началось формирование отраслевых программ цифрового перехода, в том числе в сфере энергетики. При этом цифровую энергетику следует рассматривать как неотъемлемую составляющую цифровой экономики, особым предметом которой является экономическая деятельность, коммерческие транзакции и профессиональные взаимодействия, построенные на принципах использования информационнотелекоммуникационных технологий.

Так, в [1] сделаны выводы, что существующий технологический уклад в электроэнергетике достиг предела своей эффективности и в перспективе пяти лет в ряде сфер, где потребители предъявляют более высокие требования к надежности, качеству, доступности, экологичности электроснабжения, будет иметь меньшую конкурентоспособность по сравнению с решениями цифровой энергетики. При этом характерным признаком цифровой энергетики является ее ки-берфизический характер [2]. Он становится возможен, когда так называемые интеллектуальные системы начинают формировать и использовать цифровые модели физического мира. Именно это обеспечивает самостоятельность принятия ими решений в режиме, близком к реальному времени. Для этого они должны руководствоваться не жесткими стандартами, а заданными алгоритмами, целевыми функциями и цифровыми моделями реальных электроэнергетических систем.

Методы исследования

В этих условиях оптимизация режимов электроэнергетических систем (ЭЭС) по реактивной мощности позволяет значительно повысить эффективность их функционирования. Решение названной задачи в общей проблеме оптимального функционирования интеллектуальных ЭЭС требует учета многообразия их режимов (многорежимности), определения интегральных характеристик режимов, таких как потери электрической энергии, диапазоны изменения режимных параметров и др. Непосредственный переход к многорежимным моделям резко увеличивает размерность и трудоемкость решения оптимизационной задачи.

В [3, 4] реализован стохастический подход учета многорежимности, вызванный изменением электрических нагрузок, для целей анализа и оптимизации режимов ЭЭС по реактивной мощности, позволяющий учесть стохастическую природу значительной части информации о нагрузках. Аналитическое моделирование изменения нагрузок методом факторного (компонентного) анализа дает возможность резко снизить объем информации без существенной потери точности получаемых решений. На основе полученной статистической факторной модели нагрузок реально коррелированные электрические нагрузки различных узлов ЭЭС представляются в виде линейной комбинации небольшого количества М (достаточно принять равным трем-четырем ) независимых случайных величин (коэффициентов) - главных факторов, именуемых обобщенными (ортогональными) графиками нагрузок (ОГН) [5, 6].

ОГН представляют собой совокупность статистически независимых базисных векторов, ориентированных так, что каждый из них отражает большую часть связи исходной совокупности графиков нагрузок, вносит наибольший вклад в дисперсию исходных переменных. Выделенные факторные модели отражают общие закономерности, основные свойства изменения конфигурации электрических нагрузок, обладают свойствами универсальности, придают статистическому методу и в целом процессу моделирования многорежимности свойства линейности и аддитивности и позволяют с достаточной точностью восстановить исходные параметры изменения нагрузок на рассматриваемом временном интервале [7].

Результаты и их обсуждение

В случае моделирования графиков нагрузки методом главных компонент на основе представительной выборки N исходных графиков нагрузок определяется матрица корреляционных моментов (МКМ) и выделяются М максимальных собственных чисел λi и соответствующие им собственные векторы со следующим построением ОГН:

G»=i А' М Aft )=V. ЬкМ.                (1)

Z=1                Z=1

где u'_/n, и^. - компоненты собственного вектора \н- МКМ; A Pij , A Qij - компоненты j центрированных графиков активной Pi и реактивной Qi нагрузок узла i с d интервалами постоянства.

Данное статистическое преобразование МКМ позволяет достаточно точно моделировать исходные графики электрических нагрузок Pij, Qij с помощью известных математических ожиданий MPi, MQi и моделируемых отклонений нагрузок от математических ожиданий в виде М линейных комбинации статистически устойчивых ОГН:

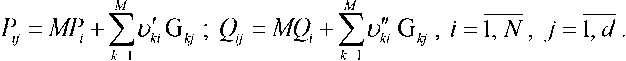
Нагрузочные потери электроэнергии получены в виде суммы основной составляющей M A E , определяемой для режима средних нагрузок, и дисперсионной составляющей oA E , учитывающей отклонение нагрузок от средних значений:

АЕ - М^ \ а\р- Ы\МУ, МЬ^Т^

1 ^{N N                 N N}         ?r\P

+ -уужуо-^^+ууодд)-—

2и^ av^ им ³ av^

• 1    ^{N N}         сГ\Р

+-УУ^8,)— 17,

• 2    и и 55,55, ^J

где M^J^MV ,МЬ^ k^Vj ) ^(^<5 _f) 4 (5,5 _f)- потери мощности, корреляционные моменты, вычисленные для модулей MVM 5 напряжений в точке, соответствующей математическим ожидани-

Э"АР a'NP a'NP ям нагрузок;---вторые производные выражения потерь мощности по со-

8У^У. a^dSj 65^6j ответствующим переменным, вычисленные относительно той же точки; N – количество узлов в схеме без балансирующего.

Статистическая модель электрических нагрузок позволяет перейти от громоздких задач определения интегральных характеристик и оптимизации, переменными которой являются часовые (поинтервальные) нагрузки, к задаче, параметрами которой выступают математические ожидания нагрузок и небольшое М число ОГН, моделирующих отклонения нагрузки от математического ожидания. Показано, что учет многорежимности ортогональными графиками приводит к значительному упрощению решения многорежимных задач. Размерность названных задач, объем вычислений резко уменьшаются. Для определения интегральных характеристик необходимо выполнить одно решение нелинейной системы уравнений узловых напряжений для режима математических ожиданий нагрузок и М решений систем алгебраических уравнений с постоянной матрицей Якоби. Решение данной оптимизационной задачи сводится к ее стандартной форме - задаче нелинейного математического программирования, для решения которой применен наиболее эффективный и широко апробированный метод приведенного – 889 – градиента (МПГ), общая структура которого описана в известных работах Л. А. Крумма, например [8] и др.

МКМ напряжений получают на основе системы уравнений, представляемой аналогично линеаризованным уравнениям узловых напряжений (УУН):

epjdbj ; dPjdvA asz.

afi/a^tWa^A^

^Qt

U = l,N ,

где АР , -, A Qi , AVi , AS i - отклонения активных, реактивных мощностей, модулей, фаз напряжений узлов от своих математических ожиданий.

Поскольку отклонения напряжений и мощностей от своих математических ожиданий приближенно связаны системой УУН (4), центрированные случайные параметры (изменения фаз и модулей напряжений) Δδ _i , Δ V_i , так же как и величины Δ P_i , Δ Q_i , аналогично (2) представляются линейными комбинациями ОГН:

м             м               __

^Ж+Е/УЗ. б^Мб.^у^,, i = VN. ^х.а.         (5)

к=\                           ^=1

После подстановки отклонений параметров режима из выражений (2) и (5) в систему (4) коэффициенты у'_ь, у^ , моделирующие отклонения фаз и модулей напряжений от средних значений, вычисляются из решения уравнений, эквивалентных системе линеаризованных УУН

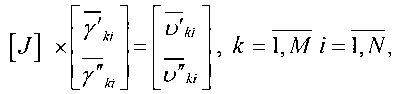
где коэффициенты u_kj у_к1 и^Д определяются с помощью исходных (восстановленных) графиков нагрузок и ОГН согласно (2) формулами вида

Р-,  ' ^V<, \/' ; р =-УО_нАО_й k = \,Mi = L N .

у 2-^ v Ч ’ to у 2-^    *4 ^Ч ^{9           9}

М у=1                  U j=x

Стохастическая модель графиков нагрузок позволяет выразить элементы МКМ напряжений и мощностей с помощью моделирующих коэффициентов

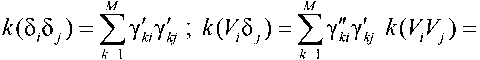
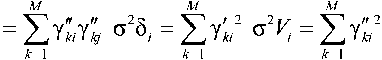
Аналогичные выражениям (8) для элементов МКМ мощностей определяются в виде мм мдру^2 U'tiu’tj, едду=2 v'Mu-tj, кЩйу к=\к=1

ММ

= T.Uki»i,j.a\Qi'i=yjyp k=Yк=\

С учетом корреляционных моментов модулей и фаз напряжений (8) традиционное выражение нагрузочных потерь электроэнергии (3) представляется в виде

NE = [ NP^MV, Мб) + оДР] T =

_   _   1 М N N