Статистическое кодирование при компрессии изображений на основе иерархической сеточной интерполяции

В настоящее время объёмы информации, соответствующие изображениям, продолжают увеличиваться. Примером может являться продолжающийся рост объёмов данных при съёмке Земной поверхности летательными аппаратами [1–3]. Если раньше распространены были только снимки с самолётов и спутников, содержащие одну или несколько компонент, то в настоящее время приходится иметь дело с мультиспек-тральными и гиперспектральными данными, которые могут содержать сотни большеформатных каналов высокого разрешения. Массовое применение беспилотных летательных аппаратов и доступность результатов их работы ещё больше усугубляет проблему объёма данных, соответствующих изображениям.

Конечно, съёмка земной поверхности не является единственным примером. Увеличение разрешения и количества изображений имеет место в различных отраслях знаний, таких как геоинформатика, медицина, полиграфия, криминалистика и т.п. Использование компрессии изображений в такой ситуации не имеет альтернативы, а актуальность повышения эффективности методов компрессии не вызывает сомнений.

Многие методы компрессии изображений основаны на декорреляции [4] данных, которые затем квантуются [5] и кодируются [6–7] (дожимаются). Например, в дифференциальных методах [8] компрессии изображений декорреляция производится посредством перехода к разностному сигналу (разности между исходными и предсказанными значениями пикселов). Разностный сигнал затем квантуется и кодируется.

В методах кодирования с преобразованием, основанных на дискретных косинусных преобразованиях [9] (JPEG [10]) или вейвлет-преобразованиях [11] (JPEG-2000 [12]), кодированию подвергается квантованное поле трансформант (результатов преобразования).

При компрессии на основе иерархической сеточной интерполяции (ИСИ) [13 –14] пиксели изображения ин- терполируются на основе прореженных версий того же самого изображения, ошибки интерполяции (постинтерполяционные остатки) квантуются и кодируются.

Во всех рассмотренных случаях в конечном итоге кодированию подвергается некий квантованный сигнал. Естественно, этап декорреляции во всех методах компрессии строится так, чтобы квантованный сигнал был как можно удобнее для кодирования («дожа-тия»). Поэтому квантованный сигнал имеет, как правило, специфичную (существенно неравномерную) плотность распределения вероятностей. Чтобы наилучшим образом использовать эту неравномерность для повышения коэффициента компрессии, квантованный сигнал обычно подвергается статистическому (энтропийному) кодированию [6 –7], т.е. кодированию, использующему неравновероятность отсчётов сигнала для сокращения объёма данных.

Таким образом, возникает задача выбора (или построения) алгоритма статистического кодирования для метода компрессии изображений. Наиболее широкое распространение имеют алгоритмы Лемпеля–Зива [15], Хаффмена [16] и арифметического кодирования [17]. Большая часть остальных алгоритмов так или иначе использует идеи, заложенные в этих трех.

Вычислительная сложность арифметического кодера достаточно велика. Ещё более существенным недостатком является то, что арифметические кодеры достаточно «плотно» запатентованы. Алгоритм Лемпеля–Зива также имеет большую сложность и, кроме того, недостаточно эффективен без дополнительного «дожимающего» алгоритма, в качестве которого обычно используют алгоритм Хаффмена. Поэтому наиболее привлекательным представляется собственно алгоритм Хаффмена, сложность которого меньше, а коэффициент является наилучшим среди всех кодов переменной длины.

Однако специфика распределения вероятностей кодируемого сигнала приводит к тому, что прямое применение алгоритма Хаффмена может повлечь за собой существенную потерю эффективности кодирования. Кодируемый (квантованный) сигнал зачастую содержит некоторое значение (обычно нулевое), которое встречается гораздо чаще остальных. Собственно причина потери эффективности заключается в том, что алгоритм Хаффмена не может назначить никакому символу (даже очень часто встречающемуся) длину кода, меньшую одного бита. Коэффициент сжатия, таким образом, не может превысить разрядности кодируемого сигнала, а объём сжатых данных (в бит на отсчёт) может существенно превысить энтропию сжимаемого сигнала, что означает потерю эффективности кодирования (заметное отставание от теоретического предела).

В данной работе предлагается двухпотоковый статистический кодер, учитывающий специфику распределения вероятностей кодируемого сигнала при компрессии изображений. Построение предлагаемого кодера производится для иерархического метода компрессии, однако предложенная идея может быть использована для широкого класса методов компрессии, основанных на декорреляции и последующем квантовании сжимаемого сигнала.

Иерархическое представление изображения

Метод иерархической сеточной интерполяции (ИСИ) [18 -19] основан на иерархическом представлении компрессируемого изображения. Изображение представляется в виде набора из L масштабных уровней. Старший масштабный уровень, т.е. уровень номер ( L -1), представляет собой двумерный массив отсчетов исходного изображения, прореженного в 2 L ^-1 раз по каждой координате. Следующий масштабный уровень, т.е. масштабный уровень номер ( L - 2), представляет собой исходное изображение, прореженное с шагом 2 L ^-2 , из которого исключены отсчеты предыдущего масштабного уровня номер ( L -1), и так далее вплоть до уровня номер 0 (рис. 1).

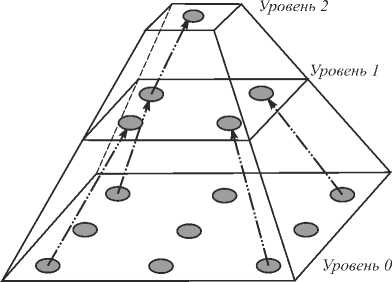
Рис. 1. Иерархическое представление изображения в виде набора масштабных уровней

Такое представление похоже на квадродерево (пирамидальное представление изображения) [4 -5], но имеет преимущество перед ним, т.к. является безыз-быточным. В формализованном виде иерархическое представление изображения X в виде набора масштабных уровней X ₁ может быть представлено следующим образом:

L - 1

X = и X I , X L - 1 = { Xl - 1 ( m , n ) } ,

¹ = ^{0                                                              (1)}

Xl = { xl (m,n)}\{ xl+1 (m,n)}, 0 < 1 < L , где {xi(m,n)} - массив пикселов изображения, прореженный с шагом 21 по обеим координатам, L - количество масштабных уровней.

Описанное иерархическое представление дает возможность компрессировать масштабные уровни последовательно, начиная со старшего уровня X l- 1 , причем пиксели более прореженных (менее детальных) масштабных уровней будут использоваться для интерполяции пикселов менее прореженных (менее детальных) масштабных уровней. Запишем процедуру компрессии формально.

Иерархическая компрессия изображения

При компрессии масштабные уровни изображения обрабатываются последовательно, от старшего к младшему, т.е. в порядке X l- 1 , X l-2 , . . X 1 , X o . Вид процедуры компрессии старшего масштабного уровня X L— 1 неважен, так как его доля в общем объёме данных очень мала (меньше чем полпроцента для числа уровней больше четырёх). Поэтому запишем процедуру компрессии произвольного нестаршего масштабного уровня X i (l< L -1), которая состоит из следующих этапов (см. также рис. 2).

• 1)    Интерполяция

К моменту интерполяции масштабного уровня X ₁ уже обработаны все более прореженные масштабные уровни ( X к , 1 <  k < L -1). Их объединение составляет прореженное с шагом 2 ^{1 +1} изображение{ x i+i ( m , n )}, для всех пикселов которого уже вычислены восстановленные значения x i + 1 ( m , n ) , совпадающие со значениями, которые будут получены при декомпрессии. Обозначим X к множество восстановленных пикселов, соответствующих масштабному уровню X k . Таким образом, интерполяция пикселов масштабного уровня X 1 производится на основе восстановленных пикселов, соответствующих уже обработанным более прореженным масштабным уровням:

Г L - 1    А

• X 1 ( m , n ) = P I U X к 1 = P ( x + 1 ( m , n ) ) ,           (2)

V к = I + 1      )

где P - функция, задающая некоторый интерполятор.

• 2)    Вычисление разностного сигнала

Вычисляется разностный сигнал, т.е. массив разностей истинных и предсказанных значений отсчетов (постинтерполяционные остатки):

f ( m , n ) = x₁ ( m , n ) - X₁ ( m , n ) .                       (3)

• 3)    Квантование разностного сигнала

Выполняется квантование приведенного выше разностного сигнала qi(m, n). При этом каждое раз- ностное значение fi(m, n) заменяется на квантованное значение:

q i ⁽ m , n ) = Q e ( fl ⁽ m , n ) ) , ⁽⁴⁾ где Q e (...) - функция, задающая некоторый квантователь, а q l ( m , n ) - квантованный разностный сигнал (или просто «квантованный сигнал»).

4) Восстановление

На этом этапе по квантованным значениям q i ( m , n ) вычисляются восстановленные значения x i ( m , n ) пикселов масштабного уровня. Для этого необходимо сначала вычислить восстановленные значения разностного сигнала:

f i ⁽ m , n ) = Q d ( q i ⁽ m , n ) ) , ⁽⁵⁾ где Q d (..) - функция деквантования, формирущая приближенное значение отсчета разностного сигнала из его квантованного значения, а затем вычислить собственно восстановленные значения:

x i ( m , n ) = f ( m , n ) + x_i ( m , n ) . (6)

Эти восстановленные значения пикселов идентичны тем, что будут получены при декомпрессии (процедура компрессии как бы включает в себя процедуру декомпрессии). Восстановленные значения нужны для интерполяции более прореженных иерархических уровней ( X k , 0< k < i ). Поэтому на этапе компрессии данная операция выполняется для всех масштабных уровней (кроме масштабного уровня X ₀). Наличие описанной обратной связи (рис. 2), то есть использование для интерполяции восстановленных, а не исходных пискелов, позволяет гарантировать, что и при компрессии, и при декомпрессии интерполятор будет работать идентичным образом (вычислять одни и те же значения), что обеспечивает возможность контроля погрешности.

5) Статистическое кодирование

Выполняется статистическое кодирование квантованного сигнала q i ( m , n ). Т.к. распределение вероятностей этого сигнала является существенно неравномерным, при кодировании можно достигнуть значительного сокращения объема данных, которое собственно и является целью компрессии изображения.

На этом описание общей структуры алгоритма иерархической компрессии завершено. Для конкретизации метода компрессии необходимо указать алгоритмы интерполяции, квантования и статистического кодирования.

В контексте настоящего исследования, посвящён-

ного статистическому кодированию, вид алгоритма интерполяции неважен. Для квантования в данной работе использовалась равномерная шкала [4 -5] ([..] обозначает выделение целой части числа):

q_i ( m , n ) = sign ( f_t ( m , n ) )

| fi ^{( m} , ⁿ )|

+ 8

max

2 s

max

+ 1

гарантирующая, что декомпрессированное изображение будет отличаться от исходного не более чем на величину заданной максимальной погрешности s ma _x:

| ^f( ( m , n )| = | ^x ( m , n )^- X ( m , n )| <  ^S max .                ⁽⁸⁾

Алгоритм статистического кодирования описан далее.

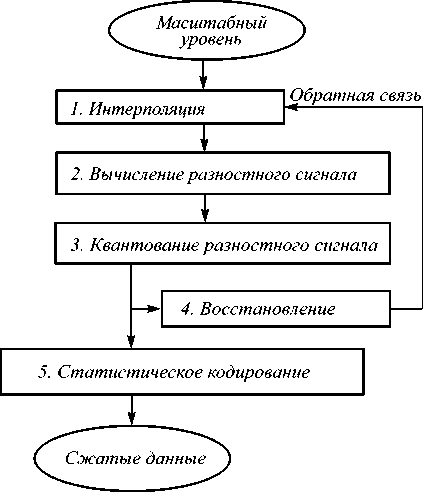
Рис. 2. Компрессия иерархического уровня X l (l < L–1)

Статистическое кодирование при компрессии изображений

Статистическому кодированию [6 -7] при иерархической компрессии подвергается квантованный разностный сигнал q i ( m , n ). Распределение вероятностей этого сигнала очень похоже на распределение вероятностей «неквантованного» разностного сигнала f ( m , n ), то есть имеет максимум в нуле и быстро спадает по обе стороны от нуля симметричным образом [4-5]. Отличие распределения вероятности квантованного сигнала заключается в том, что оно является более узким за счет объединения значений при квантовании.

Для кодирования сигналов такого вида, характеризующихся ярко выраженной неравномерностью распределения вероятностей, часто используются коды переменной длины [6] (часто встречающимся символам назначаются короткие коды, редко встречающимся - более длинные коды). Эффективность кодера в этом случае определяется средней длиной кодового слова [7], которая в данном случае совпадает с объёмом сжатых данных, который измеряется в битах на отчёт:

N - 1

в = Е Pb , (9) i = 0

где N - количество возможных значений кодируемого сигнала, p i , b i - вероятности и длины кодов кодируемых значений.

Именно среднюю длину кодового слова B и необходимо минимизировать при построении кодера. Однако согласно теореме Шеннона [6] у средней длины кодового слова есть теоретический предел: она не может быть меньше энтропии [7]:

N - 1

H = ^- E P i log 2 p>. ⁽¹⁰⁾ i = 0

Из последних двух выражений нетрудно видеть, что средняя длина кодового слова достигает теоретического предела (т.е. энтропии), если при построении кода удаётся обеспечить следующие длины кодов:

b i =- log₂ p i ,0 <  i <  N . (11)

Однако при иерархической компрессии специфика распределения вероятностей кодируемого (квантованного) сигнала зачастую не позволяет это сделать, что приводит к потере эффективности кода переменной длины для этого сигнала. Этот эффект следует объяснить подробнее.

Чем точнее интерполятор и чем большее значение имеет заданная погрешность квантования S max , тем больше нулевых значений в кодируемом сигнале. Вероятность нуля p 0 в этом случае может существенно превышать значение 0,5. Количество информации в нулевом символе равно (–log 2 (1 / p 0 )) и может быть значительно меньше одного бита при p 0 > 0,5, в то время как кодер переменной длины присваивает этому сообщению код длины один бит, за счет чего и происходит потеря эффективности кодирования, которая увеличивается с ростом погрешности, вносимой при компрессии. Чтобы избежать указанной потери эффективности, в данной работе предлагается двухпотоковый алгоритм статистического кодирования, учитывающий долю нулей в кодируемом сигнале (рис. 3).

Алгоритм работает следующим образом. Если вероятность нуля p о <  0,5, то описанной потери эффективности нет, поэтому для кодирования используется наилучший из кодов переменной длины – кодер Хаффмена [16].

Если вероятность нуля p 0 > 0,5, то кодируемый сигнал разбивается на два потока: в первый поток направляются значения всех ненулевых отсчетов, во второй поток направляется бинарная датирующая [8] последовательность: на место ненулевых отсчетов входного потока записываются единицы, а на место нулевых – нули. Далее потоки кодируются независимо.

В первом потоке наиболее вероятными символами являются 1 и (–1), причем из симметрии распределения следует, что вероятность любого из этих символов меньше 0,5, благодаря чему для кодирования первого потока может применяться стандартный алгоритм Хаффмена, который не теряет эффективности в данном случае.

Второй (бинарный) поток кодируется различными способами, в зависимости от доли нулевых значений. Если вероятность нуля не превышает некоторого порогового значения p ₀ <  p R ^LLE (т.е. вероятность нуля «велика, но не слишком»), то используется алгоритм, основанный на алгоритмах кодирования длин серий

(КДС) [7] и Хаффмена [16]. Сначала осуществляется переход от бинарной последовательности к последовательности, состоящей из укрупненных символов КДС вида 1, 01, 001, ... , 00..01, 00..00. Отличие от стандартного КДС заключается в том, что количество N RLE различных укрупненных символов может не являться степенью двойки.

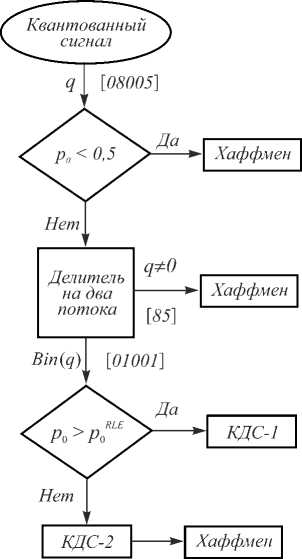
Рис. 3. Структура предлагаемого двухпотокового кодера (в квадратных скобках – пример кодируемого сигнала)

Затем каждому объединенному символу ставится в соответствие не код фиксированной длины, как в «обычном» КДС, а код Хаффмена. Для того, чтобы при этом не происходило описанной выше потери эффективности, обусловленной слишком большой вероятностью одного из символов, параметр N RLE выбирается из соотношения:

p N^{RLE - 1} <  0,5. (12)

Благодаря неравномерности распределения вероятностей объединенных символов, такое кодирование более эффективно, чем стандартный КДС, однако требует передачи кодовой книги.

Если вероятность нуля p ₀ >  p^RLE , то для бинарного потока используется стандартный КДС. От дополнительного кодирования по Хаффмену приходится отказываться из-за того, что объединенных символов становится слишком много, размер кодовой книги оказывается чрезмерно большим, что ухудшает коэффициент сжатия (адаптивное кодирование по Хаффмену также не используется, чтобы избежать чрезмерного усложнения алгоритма в целом).

Для завершения описания предложенного алгоритма статистического кодирования следует отметить, что он может использоваться не только при иерархической компрессии изображений, но и в со- ставе других методов компрессии, порождающих де-коррелированный сигнал с существенно неравномерным распределением вероятностей.

Исследование эффективности алгоритма статистического кодирования

Для исследования эффективности разработанного двухпотокового кодера он сравнивался с алгоритмами кодирования ARJ и ZIP [6–7] на специфических данных метода ИСИ, т.е. на квантованном разностном сигнале, полученном при сжатии реальных изображений. В качестве показателя эффективности в данном случае использовался объём сжатых данных B (в бит/отсчет).

Типичные результаты показаны на рис. 4 (для изображения «Портрет», представленного на рис. 5).

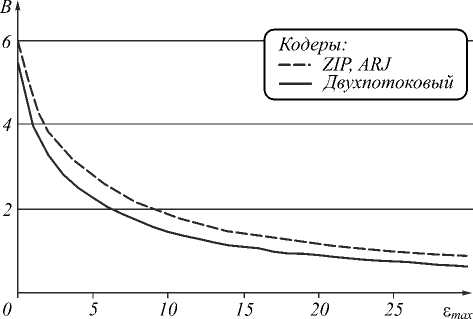
Рис. 4. Зависимость объема сжатых данных B (в бит/отсчет) от максимальной погрешности ε max для различных кодеров на изображении «Портрет»

Из рисунка видно, что на специфических данных метода ИСИ двухпотоковый кодер имеет преимуще- ство до 20 % перед алгоритмами ARJ и ZIP.

Рис. 5. Примеры тестовых изображений: «Портрет», «Пейзаж», «Картина», «ДДЗ»

Исследование эффективности иерархической компрессии, включающей двухпотоковый статистический кодер

Для исследования эффективности компрессии изображений при использовании разработанного двухпотокового статистического кодера были проведены вычислительные эксперименты на изображениях различных типов: портрет, пейзаж, картина, данные дистанционного зондирования (ДДЗ) и т.д. Примеры тестовых изображений показаны на рис. 5.

Для проведения вычислительных экспериментов предложенный двухпотоковый статистический кодер был встроен в метод компрессии на основе иерархической сеточной интерполяции (ИСИ). В рамках этого метода двухпотоковый кодер использовался для кодирования квантованного разностного сигнала. При этом в рамках двухпотокового кодера применялся «классический» (неадаптивный) вариант кодера Хаффмена, предполагающий предварительный проход по сжимаемом сигналу для оценки распределения вероятностей.

При проведении вычислительных экспериментов метод компрессии ИСИ, двухпотоковый кодер, сравнивался с методами компрессии Baseline JPEG [10] и LuraWave Wavelet [20, 21]. Для каждого из трёх указанных методов компрессии строилась зависимость объема сжатых данных B (в бит на отсчет) от максимальной погрешности ε max , вносимой при компрессии. Типичные результаты показаны на рис. 6.

Нетрудно видеть, что метод компрессии ИСИ, использующий двухпотоковый кодер, имеет заметный выигрыш у JPEG и Wavelet по объёму сжатых данных при всех рассмотренных максимальных погрешностях, кроме нулевой.

Заключение

Рассмотрены вопросы снижения эффективности алгоритмов статистического кодирования при компрессии изображений с потерями. Предложен подход к повышению эффективности статистического кодера в указанной ситуации. На примере иерархического метода компрессии произведена разработка входящего в его состав двухпотокового алгоритма статистического кодирования.

Произведено экспериментальное сравнение разработанного двухпотокового кодера с алгоритмами ZIP и ARJ в составе иерархического метода компрессии изображений, и показан выигрыш предложенного кодера. Кроме того, на серии тестовых изображений показан выигрыш иерархического метода компрессии изображений, включающего предложенный кодер, у методов JPEG и Wavelet. Предложенный алгоритм статистического кодирования может использоваться в любых методах компрессии, в которых требуется кодировать декорелированный сигнал с неравномерным распределением вероятностей.

В дальнейшем планируется сравнение эффективности предложенного двухпотокового кодера с алгоритмом, основанным на объединении часто встречающихся символов в один, а также экспериментальное исследование скорости работы предложенного алгоритма.

Работа выполнена за счет гранта Российского научного фонда (проект №14-31-00014) «Создание лаборатории прорывных технологий дистанционного зондирования Земли».

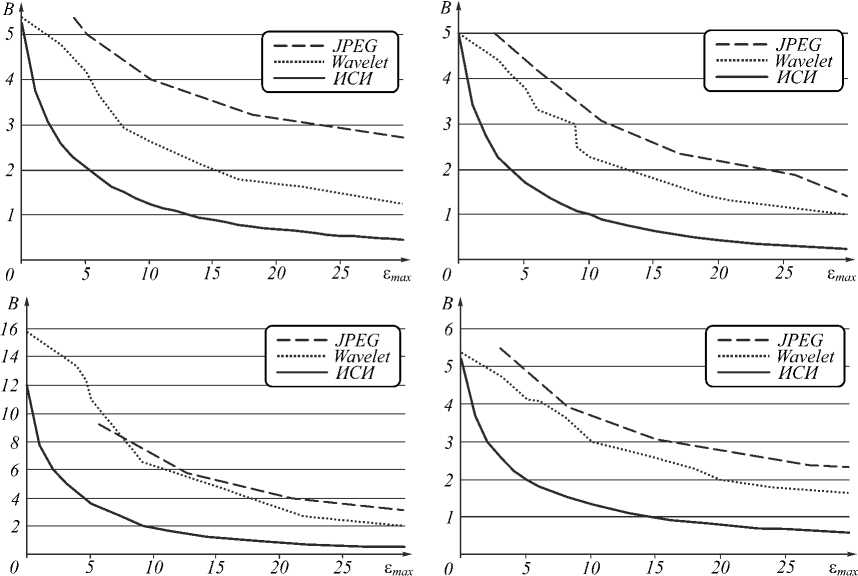
Рис. 6. Зависимость объёма сжатых данных B (в бит на отсчёт) от максимальной погрешности ε max для изображений «Портрет», «Пейзаж», «Картина», «ДДЗ»