Статистическое управление генерации пространства данных для метода дискретных элементов

Активно развиваются численные методы обоснования надежности в проектировании [1]. Переход к численным методам, включая вероятностные методы расчета [2], является логичным в современном мире при развитии теоретических подходов и вычислительных ресурсов ЭВМ. Численное моделирование ледовых нагрузок уже сейчас вытесняет традиционные нормативные расчеты. Возможность использование численного моделирования уже упомянута в некоторых нормативах [3], [4]. Численное моделирование сейчас стало использоваться для комплексного моделирования морских сооружений [5], островов [6]. При использовании метода конечных разностей или метода конечных элементов сложно точно описать поведение материала в области разрушения, взаимодействие этой области с окружающим пространством, дальнейшей накопление и взаимодействие обломков. Если применить метод конечных элементов или метод конечных разностей для рассмотрения взаимодействия материала с препятствием, то можно получить, что разрушение материала происходит путем откола фрагментов. Откол фрагментов материала на контакте с сооружением приводит к уменьшению нагрузки на препятствие. Моделирование процесса разрушения материала сеточным методом, может дать достаточно точные данные о максимальной нагрузке, передаваемой материалам при разрушении на препятствие/сооружение. Однако, в случае если нам интересно поведение обломков разрушенного материала, например их влияние на нагрузки или вибрацию, то необходимо дальнейшее моделирование, включающее взаимодействие обломков разрушенного материала между собой и с препятствием/сооружением. Данный метод реализован в программе «Particle Flow Code» [7]. Рассмотрение вопросов динамики и вибрации морских сооружений при использовании данного алгоритма рассматривалось в ряде работ [8], [9], [10], [11], [12], [13], их результаты представляют ценность для верификации численных моделей, как и работы содержащие результаты масштабных экспериментов [14].

Рассматриваемая модель, основанная на методе дискретных элементов, позволяет подробно описать процесс разрушения материала «лед» и последующее поведение его обломков. Это важно при анализе нагрузок связанных с накоплением обломков или поведением сооружения, связанным с разрушением льда, например вибрации сооружения.

Статистическое управление процессами (SPC) при расчетах разрушения сложного материала методом дискретных элементов представляет собой методологию для мониторинга, управления и улучшения расчетов и моделей с использованием статистических методов. Основная цель SPC — обеспечение стабильности процесса и снижение его вариабельности. Это достигается путём систематического наблюдения за процессом с использованием статистических инструментов, таких как контрольные карты, которые помогают идентифицировать и устранять потенциальные отклонения (рисунок 1).

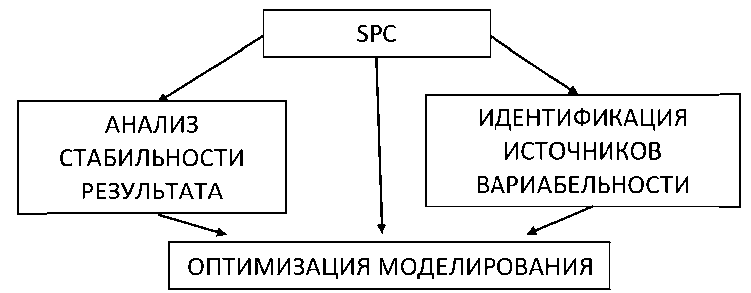
Рис. 1. Способы контроля результатов моделирования методом ДЭ с помощью SPC

SPC может быть применен не только в традиционных производственных процессах, но и в компьютерном моделировании, включая расчёты разрушения материала методом дискретных элементов. При методе дискретных элементов моделируется динамическое поведение большого количества взаимодействующих частиц, при этом твердые тела рассматривается как состоящие из группы частиц, взаимодействующих на основе законов механики и других физических принципов. SPC при расчетах методом дискретных элементов позволяет анализировать данные, полученные при моделировании, и оценивать их стабильность и соответствие ожидаемым показателям. Это особенно важно при моделировании сложных процессов, где существует высокая степень неопределённости, связанной с вариабельностью свойств материалов или параметров моделирования.

В качестве тестовой задачи для использования метода статистического управления выбрана задача о случайном генерации ледового поля для его последующего взаимодействия с сооружением в рамках ДЭ расчета [15]. Метод дискретных элементов позволяет рассмотреть динамический процесс разрушения льда. В отличие от сеточных моделей конечных элементов или конечных разностей, в методе дискретных элементов лед после разрушения продолжает участвовать во взаимодей- ствии с сооружением, тем самым периодически вызывая всплески нагрузок от льда на сооружение. Материал в плоской постановке задаче моделируется дисками разного диаметра. Данные под- ход широко используется при моделировании поведения гранулированных материалов, например при моделировании гео-механических процессов (например, устойчивость склонов). Параметры/ коэффициенты для рассматриваемой модели определялись по результатам модельных тестов, в которых образец материала при численном моделировании должен был показать такое же разрушение и передаваемые во вне нагрузки, как и реальный материал по натурным данным. Для задания

Рис. 2. Дискретно-элементная модель материала в плоской постановке задачи (элементы представлены дисками)

прочности на сдвиг использован классический закон Кулона-Мора.

Пример модельного материала, созданного алгоритмом генерации, приведен на рисунке 2. Материал, приведенный на этом рисунке, позволяет моделировать последовательное разрушение во времени.

На этапе работы алгоритма генерации ледового поля происходит формирование области, заполненной дисками разного диаметра, формирующие материал с заданной пористостью и плотностью. Формируемый диски связываются между с соседними, образуя связи. Начальные напряжения в материале сбрасываются алгоритмом генерации материала. Каждые запуск алгоритма формирует новое ледовое поле, отличное от предшествующего. Таким образом, исходные данные, и соответственно результат расчета будут иметь стохастические характер. Для получения обеспеченных значений использовалась статистическая обработка результатов. Количество необходимых прогонов моделирования с разными исходными полями льда, определялась относительной ошибкой серии экспериментов.

Основным критерием, который необходимо применять к сгенерированному ледовому полю, является критерий правдоподобности результатов, которые будет демонстрировать сгенерированное ледовое поле при расчетах. Прежде всего необходимо добиться правдоподобного разрушения и передачи нагрузки на сооружение. То есть, для ледового поля, должны в первую очередь, достоверно воспроизводится следующие величины: прочность (сжатие, растяжение, сдвиг), деформации.

Необходимо выполнить условие непрерывности, то есть в процессе генерации ледового поля, плотность его должна распределяться таким образом, чтобы не образовывалось участков с нулевым значе -нием, то есть отсутствием льда (если это не сделано специально для расчетной схемы). В противопо -ставление отсутствию «дыр» в ледовом поле, при генерации должно выполняться условие отсутствия наложения элементов, то есть в каждой точке может находится не более одного элемента (рисунок 3). Данная процедура используется в некоторых работах, например, в работе авторов Кундала и Старка [16].

Рис. 3. Материал не подходит для расчета, так как элементы имеют совпадения (а), готовый «упакованный» материал с заданной плотностью (б)

Алгоритм генерации начального ледового поля должен обеспечивать отсутствие перекрытия элементов и отсутствие напряжение в сформированной среде. На основном расчетном этапе происходит движение элементов и определение возникающих напряжений по всем направлениям (включая поворот), определение статуса связей между элементами. Растягивающие связи не восстанавливаются после разрушения.

МЕТОД

Для определения относительной ошибки и необходимого количества экспериментов, в случае стохастического алгоритма генерации материала, использовался статистический подход применительно к результатам модельных тестов.

Относительная ошибка δ для серии экспериментов определялась по формуле (1): t(n,n) •-=

*=-^ ,

где n – количество экспериментов (генераций поля дискретных элементов),

O’ – стандартное отклонение, формула (3);

tf^n) – коэффициент Стьюдента, зависящий от количества измерений n и заданного значения доверительной вероятности α ;

“ “^ – связь среднеквадратичного отклонения окончательного результата (то есть, погрешности определения среднего значения) и среднего квадратичного отклонения σ отдельного измерения;

co – среднее значение измеряемой величины x , Формула (2);

Среднее значение co измеряемой величины x указывает центр распределения, около которого группируются результаты отдельных измерений:

CO =-S?=i*,

n           L

Стандартное отклонение a , характеризует разброс результатов отдельных измерений вокруг среднего значения, которое определяется после обработки всех данных повторения измерения этой величины (нагрузки от льда). Точные значения σ и (x) являются предельными величинами, то есть их значения определяются при бесконечном числе повторных экспериментов n → ∞.

a = J^(W^W) . (3)

Коэффициент Стьюдента может быть подобран с помощью таблицы коэффициентов Стьюдента. Для серий экспериментов принималась 95% доверительная вероятность.

В случае если результаты не соответствуют контрольной карте, основанной на относительной статистической ошибке, необходимо проведение дополнительного контроля.

РЕЗУЛЬТАТЫ

Определение относительной ошибки δ проводилось параллельно расчетам для каждого выполненного численного эксперимента. Были построены графики зависимости относительной ошибки δ от количества экспериментов или вариации исходных параметров. На рисунке 4 приведен пример, показывающий поведение относительной ошибки для разного количества тестовых прогонов задачи.

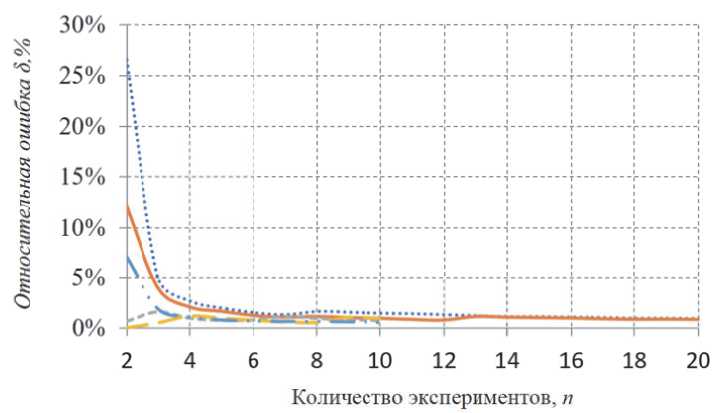
Рис. 4. Пример определения относительной ошибки δ , для нескольких серий экспериментов (каждая кривая соответствует одной серии экспериментов)

Как видно из рисунка 4, три-шесть экспериментов в большинстве случаев достаточно для получения стабильного значения расчета при относительной ошибке меньше 5%; при увеличении количества тестовых прогонов – величина относительной ошибки уменьшается.

ЗАКЛЮЧЕНИЕ

Метод дискретных элементов является мощным инструментом для моделирования динамического разрушения сложных материалов и систем, состоящих из большого количества взаимодействующих частиц. Точность и надёжность результатов моделирования методом ДЭ могут быть ограничены рядом факторов, включая вариабельность исходных параметров, численные ошибки. Применение SPC позволяет систематически отслеживать изменения параметров процесса моделирования с помощью контрольных карт, таких как карты для средних значений (стандартных отклонений) и карты для диапазона значений. Это помогает выявлять и устранять источники значительной вариабельности, что, в свою очередь, повышает точность моделирования. При моделировании гранулированного материала использование контрольных карт позволяет идентифицировать параметры, которые оказывали наибольшее влияние на отклонения в плотности упаковки и контактов между частицами. Это приводит к корректировке коэффициентов, что позволяет снизить вариабельность конечных результатов.

Моделирование методом ДЭ требует значительных вычислительных затрат, особенно при работе с большими системами или сложными моделями. С помощью SPC можно провести анализ чувствительности, чтобы выявить ключевые параметры, оказывающие наибольшее влияние на результаты. Это позволяет оптимизировать расчётные ресурсы, сосредоточив их на критически важных аспектах моделирования, а также уменьшить необходимость в дополнительных симуляциях. Применение SPC позволяет более строго подходить к процессу верификации моделей, используя статистические методы для проверки соответствия результатов моделирования установленным экспериментальным данным. Контрольные карты помогают определить, находятся ли результаты моделирования в пределах допустимых контрольных границ, что облегчает процесс оценки точности модели.