Степенные тела минимального сопротивления и аэродинамическая задача Ньютона

История решения задач о форме тел минимального сопротивления, движущихся в газах или жидкостях, восходит к Ньютону, который сформулировал подобную задачу, называемую «Аэродинамической задачей Ньютона» [1], во второй половине XVII века. Далее уже

в XVIII веке удалосв формализовать решение таких задач Эйлером и Лагранжем - создателями вариационного исчисления. Бурное развитие вариационного исчисления во второй половине XX века связано с появлением сверхзвуковых и высокоскоростных летательных аппаратов, в том числе движущихся в высоких слоях атмосферы и в космосе [2]. В 1969 году была переведена книга А. Миеле «Теория оптимальных аэродинамических форм» [3], после чего появилось множество работ на эту тему, в том числе монографий, например [4-6]. Исследования, посвященные нахождению форм тел вращения минимального сопротивления в дозвуковых, трансзвуковых и небольших сверхзвуковых потоках газа, проведены в [7-10]. Отметим, что решение таких задач связаны с большими математическими и вычислительными трудностями, для преодоления которых предложены специальные методы (например, метод локальных вариаций [11]). Другой подход решения задач о минимуме сопротивления тел вращения связан с введением пробных функций. Образующая тела вращения задается в виде функции, в которую вводят некоторые параметры, вариации которых приводят к решению задачи. Так, образующая тела вращения в высокоскоростном потоке газа представляется в виде степенной функции [12-14]. Для оценочных расчетов сил, действующих на тело при его высокоскоростном движении в газе, распространение получили формулы, найденные из локальных моделей. В основе этих моделей лежит предположение, что каждый элемент поверхности тела взаимодействует со средой независимо от других участков тела, и сила, действующая на него, зависит лишь от ориентации элемента относительно направления движения [15-17]. Эта зависимость может включать в себя скорость движения и характеристики среды (величина плотности, температура и др.), которые считаются постоянными. Наибольшего распространения получила локальная модель из [15], в которой коэффициенты давления и трения равны

Ср = ро cos² а + р1 cos а; Ст = то cos a sin а.                     (1)

Функции ро, pi, то зависят от числа Рейнольдса Reo, температурного фактора t_w (t_w = Т_ш/То, Т_ш - температура поверхности тела, То - температура торможения) и показателя степени адиабаты у, а - угол между внутреней нормалью и вектором скорости газа (рис. 1). Преимущество данной модели заключается в том, что выражения для коэффициентов давления и трения в предельных случаях по числам Нво соответствует свободномолекулярной модели газа [18] ((Нво ^ 0)) или ньютоновской модели «редкой среды» [1] (Нво ^ то):

Нво ^ 0, ро = то = 2, pi = VTt_w (у - 1) /у ,                    (2)

Нво ^ то, ро = 2, pi = то = 0.

В промежуточной области по числам Рейнольдса используются эмпирические формулы ро = 2, рі =   Tt-2- exp [- (0.125 + 0.078tw) Нво],

=______________523_____________ - _R = p_P13 _{1 +} 11^-2/³

^о    [Яі+6.88ехр(о.оо72Яі-о.ооооі6Яі²)]^1/2 ,    ^{1       о}^^{4 w} 4'

Здесь число Рейнольдса Нво = P^V^R/p (То), р (То) - коэффициент вязкости, То - температура торможения, р^, V^ - плотность и скорость невозмущенного потока газа, R - радиус основания осесимметричного тела. В данной работе на основе локального метода [15] рассматривается обтекание осесимметричных тел высокоскоростным потоком разреженного газа. Показывается, что тело минимального сопротивления обязательно имеет плоский торец, и угол между образующей такого тела и торцом постоянен для данного числа Рейнольдса и не зависит от длины тела. Показывается, что образующая степенной формы осесимметричного тела наименьшего сопротивления [19] практически совпадает с формой тела, полученной стандартными методами [3].

2.    Применение локального метода для решения задачи оптимизации

Известно с времен Нвтотона, что тело вращения минимального сопротивления имеет плоский торец. Тогда если все линейные размеры отнести к радиусу основания, то формула образующей имеет вид (рис. 1).

( 0,      0 < ж < т_о,

( у (ж), то < ж < 1.

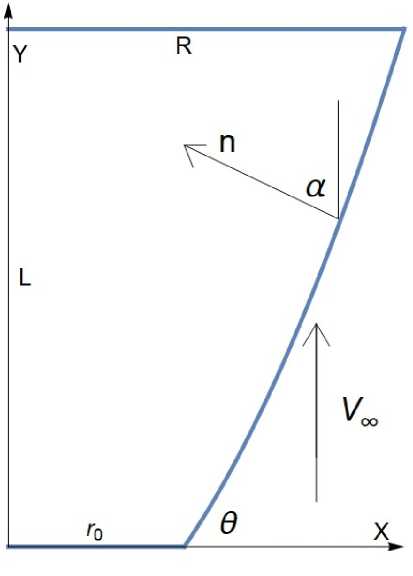
Рис. 1. Схема, обтекания тела, вращения, представленной образующей

В случае локального метода коэффициент сопротивления (сила сопротивления деленная на. скоростной напор и площадь основания) можно выразить формулой

• _{9                     х} Г ¹ ж                Г¹ ж

Сж, = (ро + Р1 - то)т2 + то + 2 (ро - то)     ——-^dx + 2рі             аж. (6)

J то ^{1 + у2}         Jr₀ V 1 + у’²

Для нахождения образующей, при которой достигается минимум коэффициента, сопротивления Сж, заменим у (ж) кусочно-линейной функцией.

Разделим высоту Т на п отрезков длиной бу. Проведем прямые через концы этих отрезков до их пересечения с кривой у (ж). Соединим точки пересечения прямыми линиями и таким образом заменим кривую у (ж) кусочно-линейной функцией (рис. 2).

Таким образом, наше тело вращения состоит из п усеченных конусов (коноидов). Очевидно, что увеличивая п или уменьшая длины этих отрезков бу, мы в конечном итоге будем приближать кусочно-линейную функцию к у (ж). Рассмотрим обтекание первого из этих коноидов (рис. 3).

Пусть справедлива модель газа Ньютона. Пусть радиус торца то, тогда (Ө = 0) с_р = 2 и сила, действующая на торец, отнесенная к скоростному напору, равна c_t = 2тгт2. Проекция силы (отнесенная к скоростному напору), действующей на боковую коническую поверхность в направлении скорости газа, равна (Sk - площадь конической поверхности)

с_к = 2

sk

cos³ 9dS_k,

^dSk = ^ж    ( 2 )

а^аж = ж V1 + tg² ө а^аж.

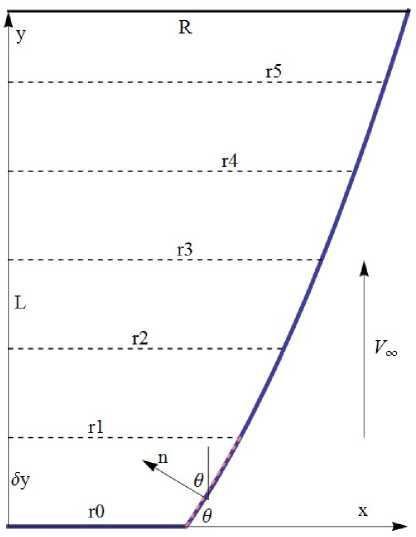
Рис. 2. Схема, замены образующей кусочно-линейной функцией

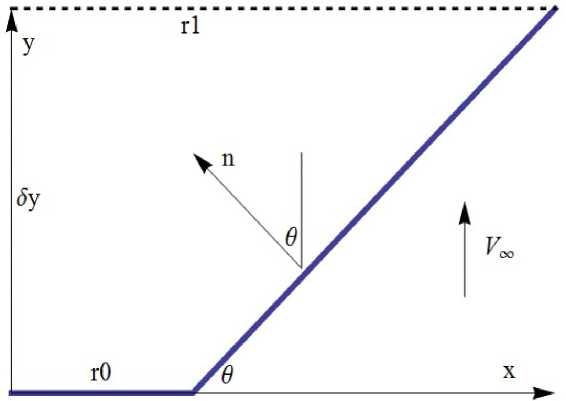
Рис. 3. Схема, обтекания коноида.

г »1           ___________ ск = 4л / cos3 Ө у1 + tg^xdx.

J »0

При заданных то, ті, бу угол Ө не зависит от ж и этот интеграл можно вычислить.

Замечая, что

cos Ө =

Vi + tgV

tgӨ =

бу

Т1 - то,

окончательно получаем

Сх_а = c-t + Ск = 2л

т0 + (т2 - то)

(ri - то)2

(ri - то)2 + бу2

)

Считая, что величины ri и бу заданы, найдем, при каком значении то функция Сх_а (то) минимальна. Типичные графики функции Сх_а (то) на рис. 4.

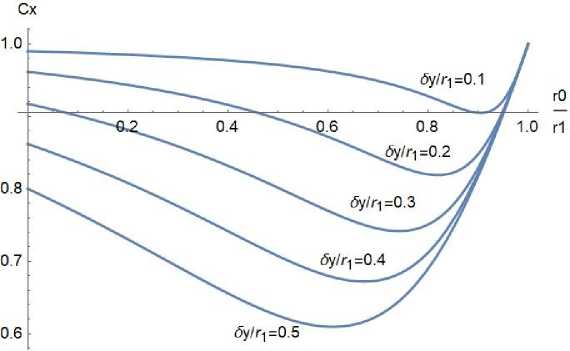
Рис. 4. Функция Сж_а в зависимости от то для разных бу

Из рис. 4. видно, что функция Сха (то) имеет минимум. Этот минимум можно вычислить из уравнения dCxa/dr0 = 0.                                    (11)

Тогда бу2 то — (то - т,)2 ті = 0;

бу² + 2т2 — ^бу⁴ + 4бу²т2 2т1

Таким образом, при любых значениях бу и т, существует коноид с радиусом сечения то, при котором сопротивление минимально (рис. 4.)

Вычислим угол Ө между образующей конуса и плоским сечением (рис. 3):

бу               2т,

.

• ^т1 ^{— т}о      бу — ^бу² + 4т2

Как уже отмечалось, при бу ^ 0 построенная кусочно-линейная функция стремится к функции у (ж) и при бу ^ 0 ІдӨ ^ 1, Ө — 450.

Из предыдущего рассмотрения следуют 2 вывода.

• 1.    Тело вращения минимального сопротивления (коэффициент давления подчиняется формуле Ньютона) обязан иметь плоский торец, величина которого зависит от его высоты и радиуса основания.

• 2.    Угол между образующей тела вращения минимального сопротивления и плоским торцом равен 450 и не зависит от его высоты и радиуса основания.

Аналогично для локального метода, используя уравнения (4), (6), (7), (9), получим коэффициент сопротивления коноида (рис. 3):

п           ,             2 , /    ,          х 2 , /         х (т12 — т02) (т1 — т0)2 ,     (т12 — т02) (т1 — то)

= С + С_Ь = Т°Г1 + (р° + ^{р —} ,°)г₀ . .. ^— Т^о)   _(Г 1 — т _о ) 2 +      + Р1 -^=^=2-.

На рис. 5 изображены кривые изменения функции Сх_а(то, бу) в зависимости от радиуса сечения то для разных бу, Reo.

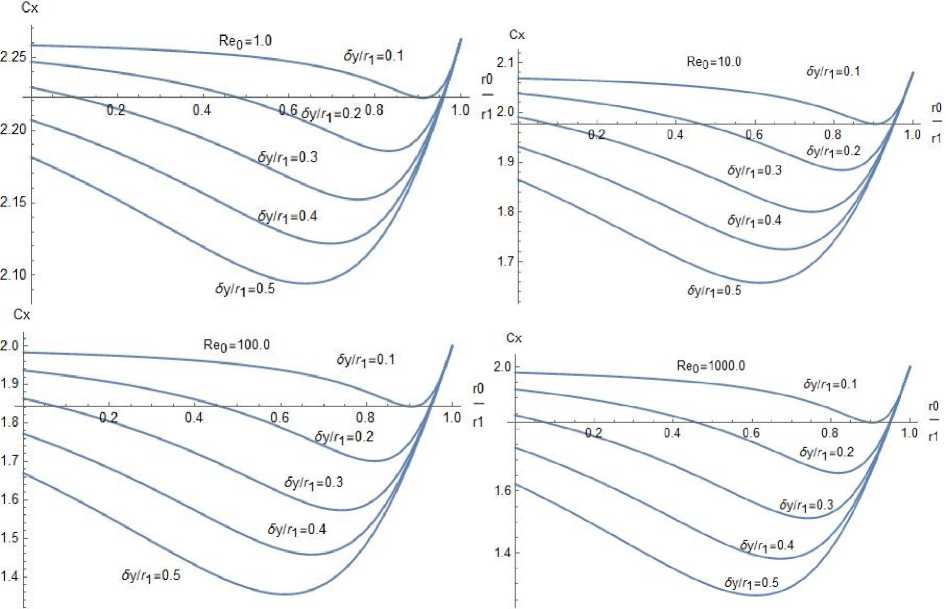
Рис. 5. Функция Сж_а ( то, бу) в зависимости от то при различивіх значениях бу, Reo

Очевидно, что для любых значений бу, щ эта функция Сж_а(то, бу) имеет минимум. Кроме того, для одинакового значения бу этот минимум уменьшается с увеличением Reo. Так же, как в модели Ньютона, этот минимум можно найти из уравнения с1Сж_а(то, бу^/йто = 0.

Решая численно это уравнение, вычислим и получим угол Ө между образующей и плоскостью.

Таблица 1

Reo	0	0.1	1	10	100	∞
Ө	51.83 0	50.540	47.310	45.260	45 0	45 0

В табл. 1 представлены результаты расчетов углов Ө для разных чисел Рейнольдса Reo. Заметим, что угол Ө меняется с 450 до 51.830 в широком диапазоне числа Рейнольдса и не зависит от высоты и радиуса основания тела.

Отнесём все линейные размеры к радиусу основания R, а силы, действующие на тело, к площади основания и скоростному напору. Тогда, в случае редкой среды Ньютона, коэффициент сопротивления можно записать так:

^Сжа = ^2т2 +

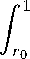
щ-^^ж. 1 + у’²

Образующая тела вращения у (ж), которая имеет минимальное сопротивление, в случае редкой среды Ньютона состоит из двух частей: 1) сначала идёт вдоль оси ж, то есть у (ж) = 0 при 0 С ж С то; 2) затем подчиняется дифференциальному уравнению Эйлера [2]:

жу’(ж) ------------2 = const = m.

1 1 + №))²]

Отсюда имеем два условия, позволяющих найти решение этой задачи:

tgӨ(тo) = у’(то),

у(ж = 1) = А(А = L/R).

В уравнении (16) заменим у' нa q, тогда

,    = q, dy = q^dq = т ^4q (1 + q2) - (1 + q ) dq dж             dq                           q

(1 + q2)2

ж = т------ q при ж = r°, q = 1, т = r°/4. Интегрируя выражение (19), получаем у = j (q2+4 q4 -ln q) +a-

Отсюда A = — 7r°/16. Таким образом, получим

/ж-то (1+^2)2,

Х 4 q ,(21)

I y= 4 (q² + 4 q⁴ — ln q — 7).

Пусть q = q* при x = 1. тогда, вс.тичина. параметра, q меняется в пределах 1 < q < q*. когда r° < ж < 1. Кроме того, при ж = 1, у = А.

Значение величины q* и r° можно определить из решения системы уравнений

( т _ то (i+q*²)²

1 = 4 q*    ,

IА = т0 (q*2 + 4q*4 — ln q*— 4).

Деля второе уравнение этой системы на первое и решая численно полученное уравнение, приближённо получаем величину q* (А). И далее мч      4q*(А)

го (А) =-------------у.

0       (1 + q2(А))2

Подставляя r° 11 1 < q < q* в (21). получаем соответствутоппіе ж іі у.

На рис. 6, 7 показаны формы степенных тел минимального сопротивления по Ньютону и совободиомолекуляриой модели. На этих графиках линии — степенные тела. [19], точки

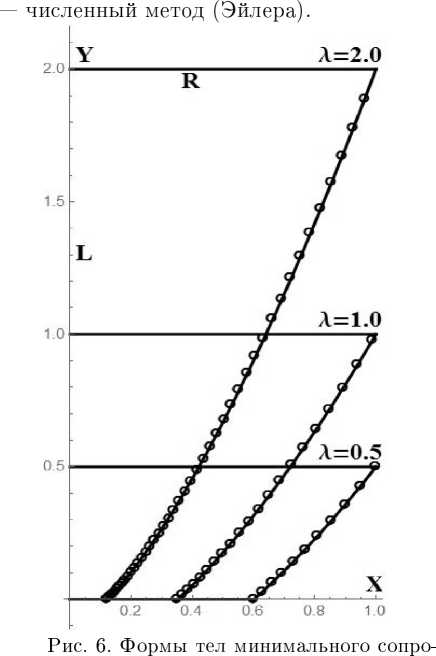
тивлепия по Ньютону

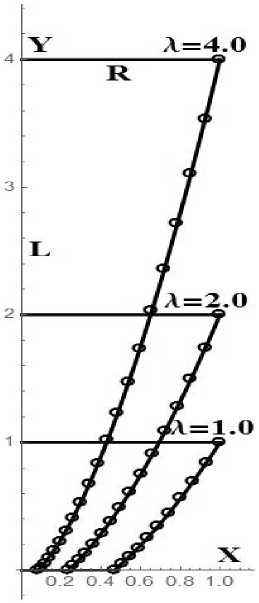
Рис. 7. Формы степенных тел минимального сопротивления для совободиомолекуляриой модели

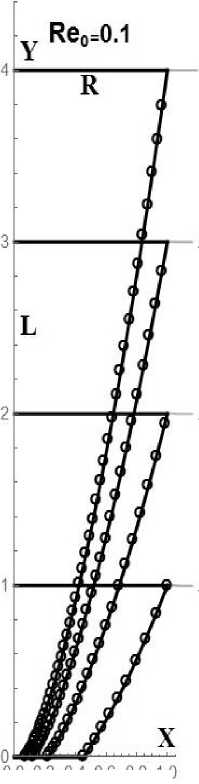
0 0 0.2 0.4 0.6 0.8 1.0

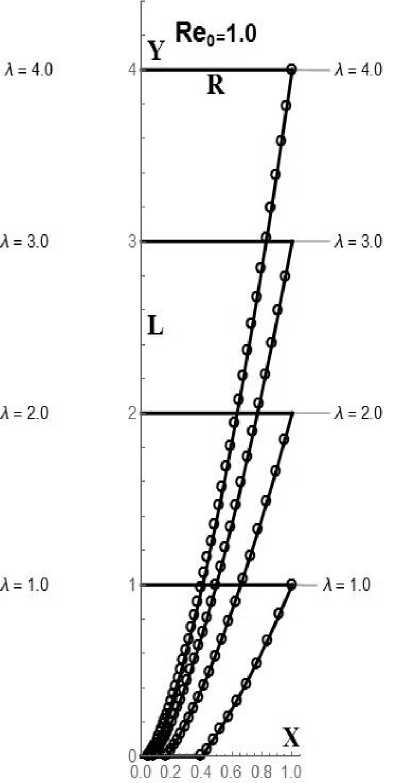
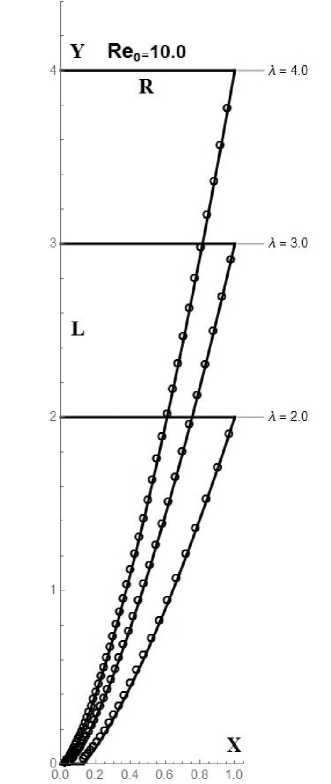
Рис. 8. Формы степенных тел минимального сопротивления в промежуточной области для разных числел Рейнольдса. Линии - степенные тела. [19], точки - численный метод

На рис. 8 аналогично показаны формы степенных тел минимального сопротивления в промежуточной области для разных чисел Рейнольдса.

Отметим, что использование разных методов позволяет получить близкие формы тела, минимального сопротивления в широком диапазоне чисел Рейнольдса.

В табл. 2 представлено сравнение радиуса, затупления тела, минимального сопротивления по Ньютону.

В табл. 3 представлено аналогичное сравнение радиуса, тела, минимального сопротивления по свободномолекулярной модели.

Таблица. 2

	А	0.5	1	2
Степенные тела.	Ы1	0.600518	0.351726	0.122667
Произвольные тела.	Ы2	0.600394	0.350943	0.12085

Таблица. 3

	А	1	2	3
Степенные тела.	Ы1	0.467696	0.235263	0.13227
Произвольные тела.	Ы2	0.467738	0.234209	0.130806

Видно, что при увеличении удлинения А, радиус затупления уменьшается в обоих случаях. Кроме того, отличие между радиусами затупления, полученных двумя методами не, более 1 %.

3.    Заключение

В данной работе представлены сравнения формы тел вращения, при которых достигается минимальное сопротивление двумя методами в высокоскоростном потоке разреженного газа. Сравнение показывает, что использование разных методов позволяет получить близкие формы тела минимального сопротивления.

Обнаружено, что одним из свойств локального метода является фиксированный угол между образующей и плоским торцом, не зависящий от удлинения.

Кроме того, проведено сравнение радиуса затупления, угла наклона между образующей тела и плоским сечением, полученных этими методами. Видно, что при увеличении удлинения, радиус затупления уменьшается в обоих случаях, а отличие между радиусами затупления, полученных двумя методами, не более 1%.