Stereo rectification of calibrated image pairs based on geometric transformation

Published Online July 2011 in MECS

Stereo matching is an important part of stereo vision, the purpose of which is that searching the corresponding feature points of stereo image pairs taken from two different views of a same scene by cameras. Since there are epipolar geometry constraints in stereo image pairs, the corresponding points’ matching is implemented along the corresponding epipolar lines. While the corresponding epipolar lines of stereo image pairs lay on the same horizontal or vertical lines, the searching space will be reduced from 2-dimension to 1-dimension. And then the complex computation of epipolar line from lots of corresponding points can be avoided, that improves the searching efficiency greatly. However, it is very difficult to ensure the epipolar lines lay on the same horizontal or vertical lines in practical application, so the stereo rectification is used to transform the corresponding epipolar lines of stereo image pairs to be that style.

Ayache[1] combined the projective matrix taken from camera’s calibration result with the condition that the corresponding epipolar lines should be in the same vertical coordinates after rectification to derive the required transformation matrix. But this method made the computation large and it requires the computation of epipolar lines in derivation Fusiello [2] improved the above algorithm to be more simple and effective, although it avoided the computation of epipolar lines, but it needed two vector cross multiplications, which increased the complexity. Hartley [3] determined the projective matrix through the constraint that the vertical difference between the corresponding points should be minimized and the epipole should be at infinity. This method didn’t need to calibrate the cameras, but it was complex as several corresponding points were required to be previous known and many variables were needed to be resolved. Min Z et al [4] improved Hartley’s algorithm by the relation between epipolar line and projective transformation, it reduced the number of variables through the features of epipolar geometry. However, since the computation of epipolar lines was inevitable, the algorithm was complex. Loop et al [5] divided rectification transformation matrix into a projective and affine component, and reduced the projective distortion which come from the process of rectification through affine transformation. But it required that all involving matrix must be positive in the rectify process, and would be disturbed easily by noise. Sui Liansheng et al [6] used projective transformation to make all corresponding epipolar lines parallel to each other, and then moved the corresponding epipolar lines to the corresponding horizontal lines by offset-value which was obtained from the optimization of minimizing the vertical difference. Although the positive of matrix was not required, the complex computation of the epipolar lines was inevitable yet. John M et al [7] computed the projective transformation through fundamental matrix, and proposed a method of reducing the projective distortion by optimizing each transformation. But it also required the computation of the epipolar lines. Isgro and Trucco [8]

proposed a method that the transformation matrix could be gained directly from the corresponding points without computing the fundamental matrix, but the corresponding points should be previous known while computing the rectification transformation matrix. Similarly, Zahrani et al [9] computed the projective matrix of rectification directly from arbitrary three groups of corresponding points in stereo image pairs, but the projective distortion depended on the selection of three groups of corresponding points, so the robustness of this method was low. Lin Guoyu et al [10] proposed an algorithm based on Hartley’s and Francesco’s, for making the rectification be more robust, the transformation matrix was calculated by the corresponding points and then was optimized by Levenberg-Marquardt method and Evolutionary Programming algorithm. Dingrui Wan et al [11] proposed an epipolar line rectification algorithm based on spherical rectification for PTZ (Pan-Tilt-Zoom) cameras. This algorithm was simple and effective, but it’s limited to PTZ cameras. As well S.Kumar [12] proposed an approach for rectifying the stereo image pairs which had different zoom and image resolution, it could be applied to the vision systems composed by the cameras of different specifications, but it needed to shrink the image and fit the zoom, and also needed to calculate the epipolar lines, so the computation was still complex.

Generally, the above methods of stereo rectification have two classifications: base on fundamental matrix and not base on fundamental matrix. The former combines the epipolar lines constraint with fundamental matrix to compute the rectification matrix. And the latter computes the matrix directly from the previous known corresponding points of stereo image pairs. However, both of them require mass and complex computations.

Recently, rectification algorithms are inclined to the stereo rectification based on uncalibrated cameras, compare with the methods based on calibrated cameras, they could save the process of resolving cameras’ intrinsic and extrinsic parameters, but most of which generally required a set of previous known corresponding points, Moreover, in the applications of stereo vision, especially in 3D reconstruction with the disparities, the intrinsic and extrinsic parameters of cameras generally should be obtained in advance. Hence, this paper proposes a novel rectification algorithm of calibrated image pairs based on geometric transformation. This algorithm establishes two virtual cameras which parallel to baseline and stay at the same height by coordinate system transformation, and then reprojects the corresponding points of the original image pairs to the virtual cameras’ image plane to finish the stereo rectification. The advantage of this algorithm is as follows: a) Avoiding the complex computation of epipolar lines or the matching process of mass previous known corresponding points, simplifying the rectification. b) Realizing the stereo rectification by coordinate system transformation, simple and easy to understand. c) The intrinsic parameters of two cameras aren’t required the same.

The remaining parts of this paper are organized as follows. In section 2, preliminaries of the rectification process are given. Section 3 is devoted to introduce our algorithm in two steps. In section 4, experiments and results are presented. The conclusion of this paper is given in section 5.

• II.    Preliminaries

• A.    Camera model

Pinhole model is a common camera model (Fig.1), the image position of an arbitrary point in 3D world is approximately described by pinhole model. Let the world point be P w ( x, y, z ) and image point be p p ( u, v ), the image point p p in the image coordinate system p I ( x I , y I ) and in the camera coordinate system p c ( x c , y c , z c ) is obtained according to geometry.

x I = ( u - u 0 )k u

У 1 = ( v - v 0 )k v

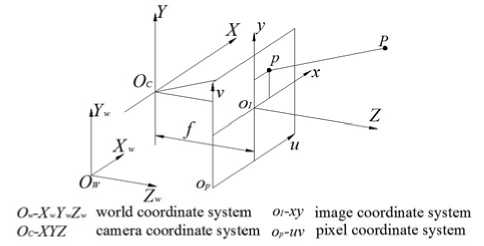
Figure 1. Pinhole Model

[ x c = ^f ■ ⁽ u - u o )/ ^f u 1 У с = ^f ■ ⁽ v - v 0 )/ ^f v [ z c = ^f

Where f is physical focal length of camera, k_u and k_v are the scale factors of the u and v axes, f_u and f_v are the product values of f and k u , k v , ( u 0 , v 0 ) is the coordinates of the principal point.

Since the cameras have been calibrated before rectification in stereo vision system, the pose between two cameras and the intrinsic parameters with each camera are previous known. And the required results in this paper are the pose of right camera relative to left and the intrinsic parameters within each camera.

L F R	= [ LRr		LT R ]	(3)
	" f u.	0	u 0 1
K L =	0	f vl	v 0 l	(4)
	o	0	1

K R

f ur	0	u 0 r
0	f vr	v 0 r
0	0	1

• B.    The configuration of stereo vision system

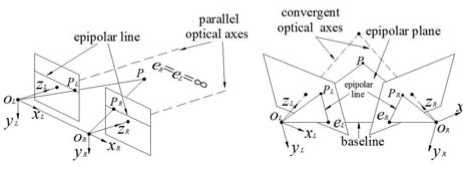
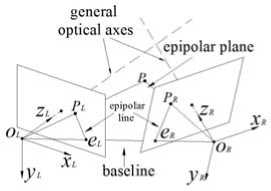
According to the position of two cameras’ optical axes, the configuration of stereo vision system is divided into three types: parallel-type, convergent-type and general-type (Fig.2). In parallel-type, the optical axes of two cameras should be parallel to each other and the intrinsic parameters are the same. Convergent-type requires that the optical axes of two cameras should intersect in finite distance. General-type is unconstrained. But to obtain larger field of view, both cameras are generally placed at the same height as possible and the angle is set a certain value. In practical it’s very difficult to make the optical axes parallel or convergent, so the common configuration of stereo vision system is general-type.

a) parallel-type

b) convergent-type

c) general-type

Figure 2. The configuration of stereo vision system

In Fig.2, the optical centers of two cameras ( O L , O R ) and the world point P constitute the epipolar plane. The intersection of the epipolar plane and the camera’s image plane is called epipolar line. Baseline is the line O_LO_R between the cameras’ optical centers, and its intersection with the image plane is defined as epipole. When the projective point in one image plane of a world point is given, its corresponding point on the other image plane is found along the corresponding epipolar line, which called epipolar geometry constraint.

Since the epipolar lines are not collinear in the general-type and convergent-type of stereo vision system (Fig.2b and Fig.2c), it needs substantial computation while using epipolar lines to search corresponding points. However, in the parallel-type the corresponding epipolar lines stay at the same height (Fig.2a) and the optical axes are parallel to each other, so that the corresponding points is directly searched along the horizontal direction. To ensure the matching efficiency in convergent-type and general-type consistent with the parallel-type, we need to transform these two types into virtual parallel-type (Fig.3), which is called stereo rectification.

р

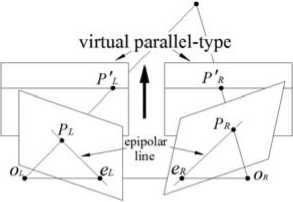
Figure 3. The schematic of stereo rectification

• III.    The rectification of stereo image pairs

The algorithm in this paper consists of two steps. In the first step, according to the position relation between two cameras which have been obtained from calibration, the original image points are converted to the coordinate system of the virtual parallel-type through coordinate transformation. In the second step, the image points which have been transformed to new coordinate system are mapped to the image plane of the virtual parallel-type by re-projecting.

• A. The transformation of camera coordinate systems

As we know the x axes of the two cameras coordinate systems coincide with baseline and toward to the same direction in parallel-type (Fig.2a), therefore the first step of stereo rectification is to compute the transformation matrix which transforms the two cameras coordinate systems to parallel-type.

Assume left camera coordinate system is L ( O L -x L y L z L ), the baseline is O L O R . And the objective is to obtain the transformation matrix of transforming the coordinate system L ( O L -x L y L z L ) to the new coordinate system L′ ( O L -x′ L y′ L z′ L ) whose x axis coincides with the baseline O L O R . First let the world coordinate system coincide with the coordinate system L and the coordinate of point O R in the world coordinate system is O R ( t 1 , t 2 , t 3 ) which have been gained from ^LT R . And then according to geometry, the conversion from the left camera coordinate system L to new coordinate system L′ is realized through rotating α around y axis of the world coordinate system and then rotating β around z axis of the world coordinate system (Fig. 4).

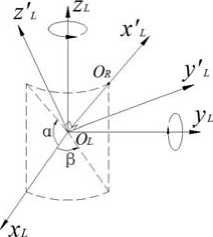
Figure 4. Transformation of the coordinate system

Then according to S. B. Niku [13], the transformation matrix of the coordinate system L′ relative to the coordinate system L is obtained:

L Fu = R ( z , в ) ■ R ( y , a )                   (6)

Where:

R ( y , a ) =	cos a 0	0 sin a 10	(7)
	- sin a cos в	0 cos a - sin в 0	"
R ( z , в ) =	sin в 0	cos в 0                    (8) 0      1

α and β is estimated by the coordinate of point O R :

sin a =

t ₃

V t 12 + t 2 2 + t 3

sin в =

t ₂

V 1 1 ² + 1 2 2

In practice, the destination is to get the coordinate of a point after being transformed from the coordinate system L to the coordinate system L′ (Fig. 3), so the required transformation matrix is about the coordinate system L relative to the coordinate system L′ . According to (6), the transformation matrix is obtained:

L ' Fl = L F - ¹ = R ^{- 1}( y , a ) ■ R ^{- 1}( z , в )

cos a ■ cos в	cos a ■ sin в	- sin a
- sin в	cos в	0
sin a ■ cos в	sin a ■ sin в	cos a

Since cameras have been calibrated, the rotation transformation of right camera relative to left camera ^LR R is already known. Then the transformation matrix of right camera coordinate system is calculated with (11).

R it it -р F R = F L R R

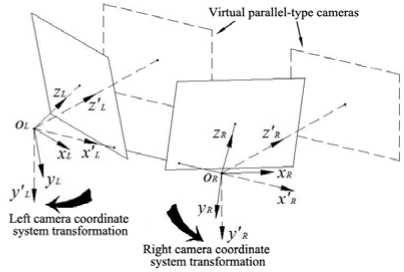
Figure 5. The schematic of the coordinate systems transformation

image information in them. To solve this problem, re-projection is implemented here. For projecting the original image points to the new image plane, the coordinates of those points in each old camera coordinate system should be previously estimated. Assume there is a left image point P pl ( u l , v l ), and then the coordinate of it in old left camera coordinate system P cL ( x cl , y cl , z cl ) is obtained with (2).

xd = f^(U l - ^U 0 1 )/ f ull Ус! = fl ⁽ v I - v 0 l )/ ^f_vl ^Zd = ^fl

Now the coordinate of the image point in new left camera coordinate system P′ cL ( x′ cl , y′ cl , z′ cl ) is obtained through the transformation matrix which has been obtained.

P d- = ^L' Fl ■ P cL                         (14)

As the same, a right image point in old right camera coordinate system is P cR ( x cr , y cr , z cr ), and its coordinate in new right camera coordinate system P′ cR ( x′ cR , y′ cR , z′ cR ) is obtained.

x cr = f r ^{( U} r y _cr = f _r ( v _r ^z cr = L

- И 0 r )/ f ur - v 0 r )/ f>„

P' = R> . p cR R cR

After getting the coordinates of the image points in new coordinate system, we need to re-project them to the image plane of virtual camera to complete the rectification. As it shows in Fig.6, P pl ( u l , v l ) is an image point of the original left camera, and the coordinate of it in the new left camera coordinate system P′ cL ( x′ cl , y′ cl , z′ cl ) is obtained after the above-mentioned method. Let the focal length of cameras be f n and the principal point be ( u′ 0 , v′ 0 ) in parallel-type system, then the projection point of P pl in the image plane of left virtual camera P′ pl is the intersection of line O L P′ cL and plane z = f n . According to mathematics, the equation of the line O_LP′_cL is as follow.

xyz x'cl y cl ^z'c l

And the intersection point P′nL(x′nl, y′nl, z′nl) is x’l = f ■ x'cjz’t nl n cl cl y'nl = fn ■ y'<^llz'd z nl = fn

Projecting the point P′ nL ( x′ nl , y′ nl , z′ nl ) to the image plane of left virtual camera is executed with (1), and the coordinate of it in pixel coordinate system P′ pl ( u′ l , v′ l ) is as follow.

u = k nu ■ x nl ^{+ И} 0 1 = f nu ■ x'd/^z'd ^{+ И} 0

. v ^c = k nv ■ y ^l + v 0 1 = f„. ■ y' d I c'd + v 0

In right original image, the corresponding image point of P_pl ( u_l, v_l ) is P_pr ( u_r, v_r ), and its coordinate in right camera coordinate system is P′_cR ( x′_cr, y′_cr, z′_cr ) which have been obtained in (16). The same with left re-projection, the projection point of P pr in the image plane of right virtual camera P′ pr is the intersection of line O R P′ cR and plane z = f n . the equation of the line O R P′ cR is as follow.

xyz x' y' z'

cr cr cr

And the intersection point P′nR(x′nr, y′nr, z′nr) is xnr = fn ■ x‘rKr y nr   fn  ycr /' zcr z ’ = f nr n

Then the coordinate of P pr ( u r, v r ) is obtained from (1), the result is as follow.

| ^U = ^f nu ■ x C rK r + u 0

1 v r = ^f_nv ■ y Cr/ z Cr + v 0

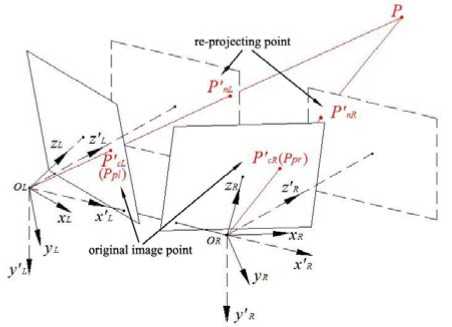
Figure 6. The schematic of left camera’s re-projection

After re-projection, the original image information is transfer to the virtual parallel-type cameras’ image plane, and then stereo matching is implemented rapidly as the rectification is finished.

• IV.    Experiments

  The proposed algorithm is tested with image pairs taken by a stereo vision system which is composed of two AVT Marlin F-080C cameras with 1024×768 resolution. The pose relationship of these two cameras is unknown, also the focal length and principal points of them is uncertain, so the extrinsic and intrinsic parameters of this stereo vision system are calculated using the calibration method which proposed by zhengyou Zhang[14] before rectification, and then the proposed algorithm is implemented after distortion correction.

Table 1 shows the intrinsic and extrinsic parameters of cameras which obtained from calibration. From ^LT R we can get α and β.

a = arcsin            ^^ ^.75            = 9.693 °    (22)

V378.77² + 15.51² + 64.75²

в = arcsin ^15.51 ----- = 2.345 °       (23)

V378.77² + 15.51²

TABLE I. The intrinsic and extrinsic parameters of

CAMERAS

	left camera	right camera
f u	3472.60	3466.08
f	3470.35	3465.03
intrinsic	0	0
s parameters u 0	583.95	633.76
v 0	447.05	514.444
	" 0.9443	0.0285 -0.3279 "
	L R R = -0.0270	0.9996 0.0093
extrinsic parameters	0.3280	0     0.9447
	L T R = [ 378.77	15.51 64.75 ] T

Then according to (11) and (12), the transformation matrixes of cameras are computed, and then the virtual parallel-type system is able to set up.

L F L =	0.9849 -0.0409 -0.1682	0.0403 0.9991 -0.0069	0.1684 " 0 0.9857	(24)
Г	0.9842	0.0684	-0.1635 "
RF = F R	-0.0655	0.9976	0.0227	(25)
[	0.1647	-0.0116	0.9863

As the intrinsic parameters of cameras are required to be identical in parallel-type stereo system, we make both cameras’ intrinsic parameters are equal to left camera’s in parallel-type stereo system, as table 2 shows. Then we re-project image points using these parameters to realize the rectification.

TABLE II. The intrinsic parameters of parallel-type

STEREO SYSTEM

	f nu	f nv	s′	u′ 0	v′ 0
left virtual camera	3472.60	3470.35	0	583.95	447.05
right virtual camera	3472.60	3470.35	0	583.95	447.05

For verifying our rectification algorithm’s feasibility and effectiveness, experiments have been divided into two parts. The first part of experiments is implemented on chess board which has been used to calibration. A pair of chess board images before and after rectification is presented in Fig. 7, and table 3 shows that the vertical coordinates and the vertical disparities of the corners marked in the images. From the chart it can be seen that the corresponding corners don’t lay on a same horizontal lines before rectification, but the vertical disparities of them almost equal to zero after rectification, so the proposed algorithm is feasible.

a) Before rectification

TABLE III.      The Vertical Disparities of Corresponding

Corners Before And After Rectification

b) After rectification

Figure 7. Pair of chess board images before and after rectification

The vertical coordinate before rectification(pixels)			The vertical coordinate after rectification(pixels)
Left image	Right image	Vertical disparity	Left image	Right image	Vertical disparity
193.701	218.365	-24.664	186.376	186.449	-0.073
184.647	184.647	-26.540	183.908	184.003	-0.095
251.931	276.836	-24.905	246.551	246.577	-0.026
247.569	274.702	-27.133	245.656	245.662	-0.006
311.045	336.991	-25.946	307.345	307.302	0.043
301.224	334.224	-33.000	305.947	305.912	0.035
374.354	398.336	-23.982	368.868	368.866	0.002
365.674	397.281	-31.607	367.878	367.975	-0.097
437.04	459.207	-22.1672	430.432	430.398	0.034
421.139	459.230	-38.091	429.355	429.288	0.067
493.130	520.632	-27.502	491.899	491.858	0.041
544.617	584.41	-39.794	553.727	553.802	-0.075
611.569	645.644	-34.075	616.310	616.234	0.076

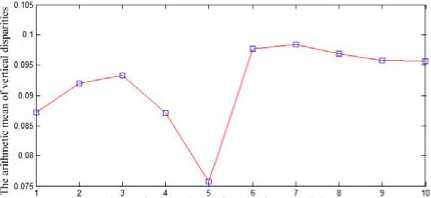
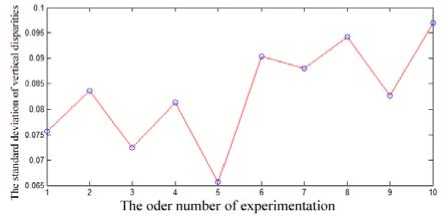
In order to verify the proposed algorithm more effectively, we have ten pairs of chess board images to experiment, and calculate the arithmetic mean value and standard deviation value of all corresponding corners’ vertical disparities after rectification (Fig. 8). From the chart it can be seen that the arithmetic mean value and standard deviation value are less than 0.1 pixels. This indicates that our algorithm can effectively realize the stereo rectification.

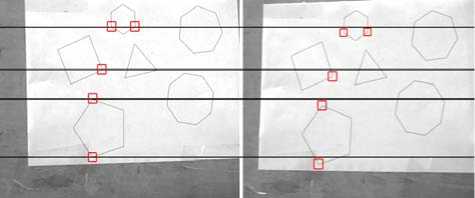
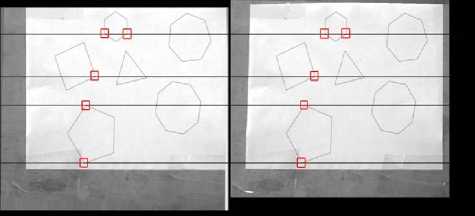
The second part of experiments is carried out by several image pairs of real scene to verify the practicability of our algorithm. Fig. 9 is the image pairs of a board on which a paper with the principal geometric shapes is pasted. Before rectification, the corresponding corners do not stay along the same horizontal lines. And after rectification, all corresponding corners are transferred to the corresponding horizontal lines. From this result, the algorithm in our paper is practical.

The order number of experimentation

a) Before rectification

a) The arithmetic mean of vertical disparities

b) The standard deviation of vertical disparities

Figure 8. The statistical results of experiments

b) After rectification

Figure 9. A board with principal geometric shapes

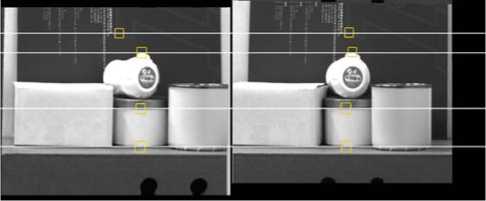
Fig.10, 11 and 12 show the comparison diagrams of before and after rectification of the real scene images which taken by the stereo vision system with different pose relationship between the two cameras. Before rectification, the corresponding features of both images which marked in figures lie in different horizontal lines, as Fig.10a, 11a and 12a show. But after rectification, the corresponding features lie in the corresponding horizontal lines in Fig.10b, 11b and 12b. From these experimental results, the rectification algorithm in this paper is available for real scene images, and also effective for different configuration of stereo system.

a) Before rectification

b) After rectification

Figure 10. Rectification of one real scene image pairs

a) Before rectification

Figure 11. Rectification of another real scene image pairs

a) Before rectification

Figure 12. Rectification of the third real scene image pairs

b) After rectification

• V.    Conclusions

An algorithm of stereo rectification based on calibrated cameras with coordinate system transformation is presented in the paper. After getting the intrinsic and extrinsic parameters of cameras from calibration, we can combine the invariance of cameras’ optical centers with coordinate system transformation to establish a virtual parallel-type stereo vision system at first, and then re-project all the original image points of left and right cameras to the new image plane of each virtual camera by geometry, finally finish the whole process of the rectification. This algorithm avoids the complex computation of epipolar lines or fundamental matrix, also omit the matching process of large corresponding points in uncalibrated cameras’ rectification, and it is more simple and intuitive than previous algorithm. At last, various experiments have been carried out and the results show the proposed algorithm is effective and feasible.

Acknowledgement

The work described in this paper was supported in part by a grant from Program for New Century Excellent Talents in Fujian Province University (Project no. XSJRC2007-07).