Stochastic Model Including Refining Stage to Improve Water Supply System in Bangladesh

Stochastic programming (SP) is a mathematical model that addresses uncertainty in some or all variables and parameters by utilizing well-known probability distributions [1, 2]. The main objective of SP is to identify a solution that optimizes a set of predetermined criteria while accurately accounting for uncertainty in the problem parameters. Various industries; including energy optimization, transportation, water supply systems, and finance, encounter uncertainties, making stochastic programming an invaluable tool for them. In this study, we applied SP to the water supply system in Bangladesh. This paper will explore the importance of SP in water supply planning and management, providing examples of its successful applications in real-life scenarios. Access to water is essential for human life and the economic development of a country. However, Bangladesh faces several challenges, including climate change, a growing population, urbanization, and land use practices, all of which impact the reliable availability of water. Effective water supply planning requires a comprehensive strategy that considers the system's risks and uncertainties. By incorporating random variables, SP offers a powerful approach to optimizing the water supply system [3].

Water is a fundamental necessity for humans, animals, and plants alike. Although water covers 75% of the Earth’s surface, fresh water supplies remain limited. Dhaka, the capital city of Bangladesh, has a population of over 20 million people and is encircled by four rivers: the Buriganga, Turag, Dhaleswari, and Shitolokka. Ensuring a proper water supply and a functioning sewerage system is essential for the city's health and well-being. The Dhaka Water Supply and Sewerage Authority (DWASA) is responsible for providing these services, covering an area of 360 square kilometers. To manage the supply, Dhaka is divided into ten sections. DWASA sources 67% of its water from groundwater and 33% from surface water [4, 18]. However, groundwater levels are declining at a rate of about 3 meters annually [5]. The city requires between 2,550 and 2,600 million liters of water per day, with a supply that typically ranges from 2,650 to 2,700 million liters [5, 6, 18]. Unfortunately, a lack of sustainable planning means that urban poor residents are often deprived of their basic need for clean water. Authorities must prioritize providing safe drinking water to these communities. While rural areas face pollution primarily from agricultural and natural sources, urban industrial centers like Dhaka suffer from pollution due to anthropogenic factors, including untreated industrial effluent and municipal waste [7].

Industrial effluents, untreated sewage, and agricultural runoff have contaminated numerous rivers and waterways in Bangladesh. This pollution also has an impact on aquatic ecosystems, public health, and water quality. Bangladesh because of institutional fragmentation, poor infrastructure, and insufficient capacity for integrated water resource management make it difficult to effectively control and manage water resources [4, 5]. Due to the enormous amount of pollution that people in cities discharge, river pollution is particularly severe and serious in South Asian countries like Bangladesh, India, and Nepal. Pollution levels have been rising consistently, almost in parallel with urbanization, according to regression analysis [6]. Bangladesh's rapid urbanization and industrialization are polluting both surface and groundwater, and most significantly, arsenic contamination and industrial waste are compromising the natural resource's potability. The people of Bangladesh have not been able to receive environmental justice due to ineffective water management and inadequate legal enforcement [7].

In 2017, Mir et al. [12] developed a probabilistic, mixed scenario-based, two-stage stochastic programming model to design integrated wastewater collection and water delivery systems (WSWCS). This model accounts for both hazards and uncertainties arising from business-as-usual scenarios. Similarly, Xiaowen et al. [13] created a stochastic multiobjective chance-constrained programming model (SMOCCP) in 2017 to address water supply management challenges in the Xiaoqing River watershed. In 2012, Uri et al. [14] introduced a sophisticated methodology known as Limited Multi-Stage Stochastic Programming (LMSP) to manage water quantity and salinity in a seasonal, multi-year water supply system. In this approach, the number of stages and scenarios increases, which correlates with a linear increase in the total number of choice variables, while the number of decision variables at each stage remains constant. The LMSP identifies decision nodes that make similar choices by solving several deterministic optimization problems and employing a decision clustering framework. Additionally, in 2011, Donald et al. [15] developed a model to evaluate the risks to municipal water supply systems posed by population growth and climate change. They utilized an artificial neural network (ANN) with deterministic properties, along with time series Monte Carlo simulations, to simulate daily water demand under varying climate conditions, taking into account the uncertainties in water usage.

With a large urban population, Dhaka city is currently facing numerous challenges in various developing sectors, with water service being one of the most crucial ones. Despite the government's ultimate responsibility to provide appropriate water services to its residents, the government's formal water service systems still fail to serve many urban poor people living in slums or other informal settlements. Dhaka city is using a combined approach of surface water (such as treated river water), rainfall, and limited groundwater extraction to address the current conditions. This study will develop a two-stage stochastic programming model for the management of environmentally harmful wastewater. The model assumes that wastewater refines at the refining stage and subsequently reaches the secondary demand point for use. The extra water will be released into the river, ensuring that the refined wastewater does not harm the ecosystem of the water source. We analyze the effectiveness of the proposed mathematical model and solution process through a real-world case study. The results illustrate the value of the generated stochastic programming model and the effectiveness of the chosen strategy as a solution.

The paper is structured in the following manner: The methodology of multistage stochastic programming (SP) and recourse problem (RP) will be discussed in Section 2. Section 3 will discuss the water supply system, including refinement steps, and analyze solutions for various scenarios. Section 4 will include the computation of system costs, both with and without refinement, utilizing the suggested models. Investigations of the EVPI and VSS will be presented in Section 5. A sensitivity analysis will be demonstrated using risk averse (RA) optimization in Section 6. Finally, will provide the paper's conclusion. The suggested model is expected to support the improvement of the water delivery system and effectively meet water demand.

2.    Methodology

This section focuses on two-stage and multi-stage stochastic models.

Two-stage stochastic linear programming model takes the following form:

min : c T x + E[Q(x, Q] xeR n

s.t. Ax = b, x >  0

where Q (x, ^) is the optimal solution of the second-stage model min : qTy yeRm

• s. t. Tx + Wy = h,y >  0

Here, x £ Rn: First-stage decision variable y £Rm: Second-stage decision variable, also called recourse variable c £Rn: Cost coefficients for first-stage decisions (e.g., cost per unit of production).

A £Rpxn: Coefficient matrix for the first-stage constraints.

b £R₽: Right-hand side of first-stage constraints (e.g., resource availability).

q £R ^m : Cost coefficients for second-stage decisions (e.g., penalties for recourse actions).

W GR mxm : Recourse matrix in the second-stage problem.

T GR mxn : Coupling matrix linking first-stage and second-stage decisions.

h £R ^m : Right-hand side of the second-stage constraints (e.g., demand to be met).

ξ(q,h,T,W): Random variable representing uncertainty [2, 4].

In multistage stochastic programming, decisions are made in a sequential manner. Initially, a decision is taken without any prior observations. Based on this decision, an observation is obtained, which then informs the second-stage decision. This process continues, where each stage relies on the observation obtained from the previous stage, until reaching the T-th stage decision after receiving observations from all preceding stages [1, 2, 8]

Suppose that a linear programming problem is given by min : CX

n

xeR n

s.t. Ax = B,X >  0

where the right-hand side constant B is uncertain with different discrete realization B1, B2, …., Bk with probabilities p1, p2, …., pk. Before the realization of the random variable B, it must take the decision of the first stage decision X without any prior information. After revealing the value of B a second stage decision Y called the recourse action, is need to adjust the decision X so that the constraints satisfy and minimizes the objective function value. To find the recourse variable Y, solve the following optimization problem min : QY

n

xeR n

s.t. AX+WY=B,Y ≥ 0

Where W is the interaction matrix between the variable X and Y. For different realization, interaction matrix can be different and the linear programming problem equivalent to (3) and (4) takes the following form [16]:

Min CX + p i Q i Y i + p 2 Q 2 Y 2 +... + p k Q k Y k

Subject to : A₀X = B_o

AX + WY = Bj

AX + W₂Y₂ = B

AX + W₂Y₂ = B

M

AX + W_kY_k = B_k

X >  0,Y >  0,Y₂ >  0,...,Y_k >  0

3.    Water Supply Model with Refinement Stage

Paul and Jonathan developed a two-stage stochastic programming model in 2003 to meet a city's water demand, considering the availability of water at the authority as an uncertain parameter. They did not consider the refining stage. As a result, the city emits their used contaminated water to the environment [17]. In this section, a model is developed where the wastewater emits into the water source after refinement. Here, we have proposed one additional step in the model that the wastewater emits to the water source with refinement and will not discuss what the refining process. The proposed model is discussed as follows.

Dhaka water supply and sewerage authority (DWASA) provides water to the community of 20 million people of Dhaka. 1 unit of water is considered as 1000 liters, and cost and revenue are measured in Bangladeshi Taka (BDT). The authority supplies water to the community at a cost of C BDT per unit. It sources this water from the Buriganga River at a cost of cj_ BDT per unit. The maximum supply capacity of the authority is L^ units. If the authority is unable to meet the community’s water demand, the community will obtain water from a second water supply authority. This secondary authority provides the first ^2 units of water at a cost of C4 BDT per unit, and the subsequent ^3 units at a cost of ^5 BDT per unit. Any extra water from the first authority is sent to the secondary demand point, generating a profit of C2 BDT per unit. It is assumed that the community uses 50% of the water for sanitary and drinking purposes, while the remaining 50% is refined at a cost of ^З BDT per unit during the refining stage [3]. The refined water is then sent to the secondary demand point, providing a profit of Су BDT per unit, while any remaining water is released back into the river, generating a profit of C^ BDT per unit. The community's water demand is d^ units, and the demand at the secondary demand point is dy units. The first authority can collect a maximum of ^4 units from the river. During the refining stage, it is assumed that there is a system loss of 10%, meaning that 10% of the water is lost in the process [3]. The water supply model is shown graphically in Fig. 1.

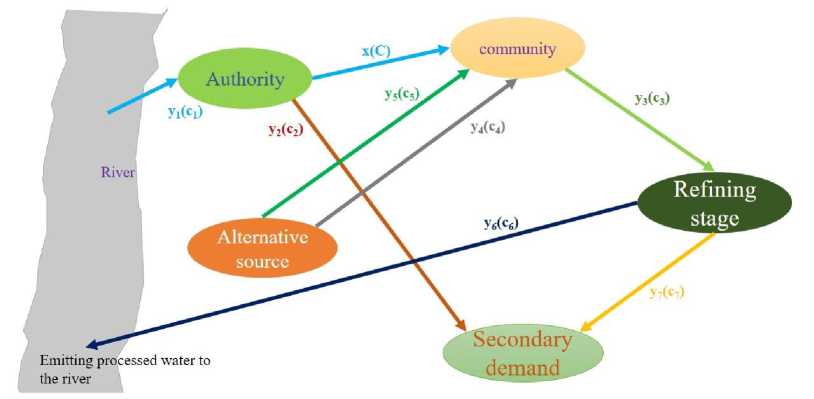
Fig. 1. Water supply system

In Fig.1., the values in brackets indicate the cost coefficients of the corresponding variables.

• 3.1    Model Formulation and Solution

The scenario illustrated in Fig.1. presents a two-step decision-making process. An initial decision x is followed by a second-stage decision У . During the transition from the first stage to the second stage, a random event occurs, introducing uncertainty. This situation is often referred to as making decisions with recourse, as the initial decision is made in the presence of uncertainty.

Let x = quantity of water supplied to the community by the first authority.

• У 1 = quantity of water that the first authority collected from river.

• У 2 = quantity of water that is supplied to the secondary demand point.

Уз = quantity of water that is refined.

• У 4 = quantity of water supplied by another authority to the community at a cost C^ per unit.

Уз = quantity of water supplied by another authority to the community at a cost C^ per unit.

Уб = quantity of refined water discharged into the river.

• У 7 = quantity of refined water supplied to the secondary demand point.

Let’s assume that “b” represents the amount of water reserve at the first authority. If we know the value of “b” we can solve the problem using deterministic linear programming. However, since the value of "b" is uncertain, we need to employ stochastic optimization to address the problem effectively.

To solve the water supply model, we establish the constraints based on water conservation at each node. The linear programming problem for this water supply system is presented below, with the assumption that the value of “b” is a known quantity.

Min z = Cx + ^С1 У 1 + ^С2 У 2 + ^сз У з + ^С4 У 4 + ^С5 У 5 + ^Сб У б + ^С7 У 7 Subject to : x - yj + y₂ = b ( water conservation constraints at the first authority )

x — Уз + У4 + Уз = di ( water conservation constraints at the community ) restricting to refinement of 50% of the water that the community uses for washing purposes water conservation constraints during the refining stage with system losses water conservation constraints at the secondary demand point

x ^{- 2}У з ⁺ У 4 ⁺ У 5 = ⁰

0.9У 3 ^- У 6 ^- У 7 = ⁰

У 2 ⁺ У 7 = ^d2

0 < x < L 1 ,0 < y 1 < L 4 ,0 < y 2 < L 4 ,0 <  У з < L 4 ,0 < y 4 < L 2 ,0 < y 5 < L 3 ,0 < y 6 < L 4 ,0 < y 7 < L 4

The aim of this study is to reduce the system costs associated with water supply to the community. According to the preceding Fig.1., the arcs are indexed by the variables. In this context, the first subscript indicates the variable corresponding to the arc identified by a numerical number, while the value in brackets represents the cost coefficient for that particular arc. We use the variable to denote the decision that must be made immediately, before the actual random variable is observed. Conservation of water flow is necessary at the initial authority stage, within the community, during the refining stage, and at secondary demand points; however, there is no need for conservation near the river's source. The definition of recourse variables for each potential realization leads to the formation of the Stochastic Programming (SP) model.

= flow in realization k along arc j.

= is the probability of each realization; where n is the number of realizations. Then the stochastic recourse programming problem, when b is uncertain is as follows:

n7

^Minz = Сх + p ^^ Ky mJ k = 1 m = 1

Subjectto:x - у* + y₂ k = b k

• ^{x -} y ak ⁺ y 4k ⁺ y₅ k = ^d1

• ^{x - 2} y ak ⁺ y 4k ⁺ y₅ k = ⁰

⁰ .9y ak ^- y 6k ^- y 7k = ⁰

^y2k ^{+ y}7k = ^d2

0 <  ^x <  L 1 ,O <  y 1k ,y₂ k ,y 3 _t,y 7k ,y 6k <  ^L4 , ⁰ <  y 4k <  ^L2 , ⁰ <  y₅ k <  ^La^,k = ^{1,L ,n}

Now solve this model using a raw value of the cost coefficient perspective to Bangladesh. Assuming the cost coefficients are = 0,   = 10,    = -5․83,    = 5,,    = 11․66,    = 8․33,    = 0,    = -5.83, that is, the community gets water from the authority at zero cost, and the community emits refine water to the river at zero profit [7].

To minimize the total system cost, we will consider profit as a negative value. Let's assume that the community demands 32 units of water, while the secondary demand point requires 15 units. The authority can extract a maximum of = 45 units of water from the river. The values for and are 15 units each, and the value of is 36 units. Consequently, for realizations or scenarios, the deterministic linear programming problem that corresponds to the stochastic programming problem can be structured as follows:

n

Minz = 0x + p ^ (10y 1k - 5.83y 2k + 5y ak + 11-66y 4k + 8-33y 5k + 0y 6k - 5-83y 7k )

k = 1

Subjectto:x - y ik + y 2k = b i

• ^{x -} y ak ⁺ y 4k ⁺ y 5k = ³²

^{x -} 2y ak ⁺ y 4k ⁺ y 5k = ⁰

⁰-^9y ak ^{- y} 6k ^{- y} 7k = ⁰

y 2k ⁺ y 7k = ¹⁵

0 < x < 45,0 < yik < 36,0 < y2k < 36,0 < yak < 36,0 < y4k < 15,0 < y5k < 15,0 < y6k < 36,0 < y7k < 36, where k = 1,L ,n.

For different scenarios, various amounts of water are available, and the objective function value corresponding to the number of realizations is shown in Fig.2.

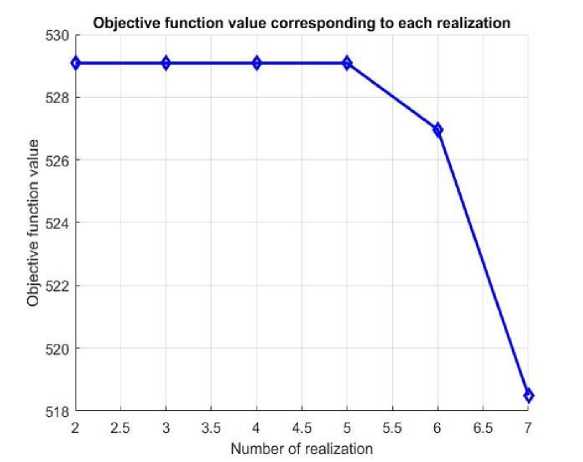
Fig. 2. Water supply system cost for different realization

The graphical representation of the underlying variables for various realizations is shown in Fig. 3.

1 2345 0 7  1234507  1234567

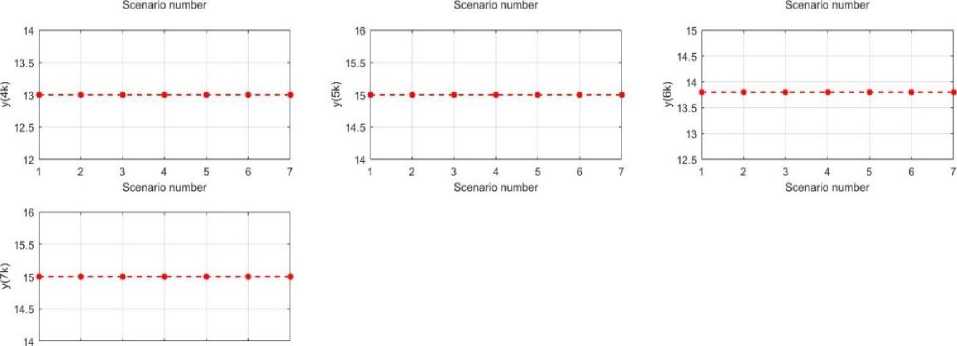
1       2       3       4       5       6       7

Scenario number

Fig. 3. Solution of the recourse variable

As the number of scenarios increases, more sample data is captured. When sample data is captured more, the decision becomes more accurate, and it is observed that when the number of scenarios increases in the above model, the water supply cost becomes smaller.

The solutions of the variables У2k for each realization к are zero. This indicates that the authority cannot supply water to the secondary demand point. The authority collects water from the river at a cost of 10 taka and earns a profit of 5.83 taka per unit of water supplied to the secondary demand point. It is important to note that the solution for the recourse variable У1к monotonically decreases when the availability of reserve water for the authority increases. Meanwhile, the solutions for the other recourse variables remain unchanged despite the increase in water availability. To find the optimal solution that satisfies the equality constraints in the proposed model, we must ensure that it produces the same solution as the other recourse variables. The increasing availability of water at the first authority is counterbalanced by the variable y±k . Specifically, when water availability increases, the value of the variable yrk decreases. This adjustment ensures compliance with water conservation at the first authority while maintaining consistency with the solutions of the other recourse variables. This phenomenon occurs because yrk and are governed by the same constraints and do not interact independently with the other recourse variables. As a result, the solutions of these other recourse variables maintain the same value to satisfy the equality constraints.

4.    Model Analysis Using Raw Data Perspective to Bangladesh

Now analyze water supply system cost without refining process. The cost of 7 years from 2016 to 2022 which was collected from DWASA [18] is presented in the Table 1.

Table 1. Cost coefficients

Cost coefficients	2016	2017	2018	2019	2020	2021	2022
c 1	10	10.5	11.02	11.57	14.46	15.18	15.94
c 2	5.83	6.13	6.43	6.75	8.44	8.86	9.3
c 3	0	0	0	0	0	0	0
c 4	11.66	12.25	12.86	13.5	16.87	17.71	18.6
c 5	8.33	8.75	9.18	9.64	12.05	12.65	13.28

To solve the model AMPL programming language is used. The total water supply system cost is shown in Fig. 4.

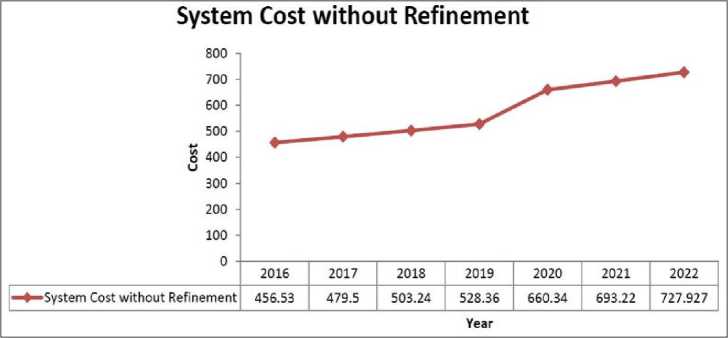
Fig. 4. System cost without refinement

From the above analysis, it is observed that the equivalent cost of y_3k in the model dropped from 5 to 0. Because 50% of the wastewater was filtered in the proposed model at a cost of 5 taka per unit. But in these cases, do not consider the refining process; as a result, the cost of refining per unit of water becomes zero. Because the constraints matrix remains consistent across all instances of the water supply model, the optimal solution for the recourse variable stays the same in every case. However, varying cost coefficients yield different optimal values for the objective function. That is, the feasible region is the same for all cases. So, for the calculation of the optimal system cost, the formula с^T x (solution of the recourse variables) for different cost coefficient matrix c for different years can be used.

• 4.1    Model Analysis with Refinement

  Cost data is collected from DWASA regarding the supply of water to residents. DWASA raises the water price by 5% each year. In 2020, they implemented a significant increase of approximately 25%. They cite several reasons for these price hikes, including rising production costs, transportation expenses, and increasing electricity and gas bills. In the proposed model that includes a refining stage, 2016 is considered the base year. It is assumed that when factoring in the refining stage, the water collected from sources by DWASA is not contaminated, and production costs will increase at a slower rate. Therefore, the water price should be increased by 3% annually, with a price hike of 15% planned for 2020 [18].

The seven possible cost coefficients that the DWASA would pay in the years 2016 to 2022 to provide water to the population are shown in Table 2.

Table 2. Cost coefficients

Cost coefficients	2016	2017	2018	2019	2020	2021	2022
c 1	10	10.3	10.609	10.9273	12.5664	12.9434	13.3317
c 2	5.83	6.0083	6.1866	6.3742	7.3304	7.5503	7.7768
c 3	5	5.15	5.3045	5.4636	6.2832	6.4717	6.6658
c 4	11.66	12.0167	12.3772	12.7485	14.6608	15.1006	115.5536
c 5	8.33	8.5833	8.8408	9.1081	10.4720	10.7861	11.1097
c 6	0	0	0	0	0	0	0
c 7	5.83	6.0083	6.1866	6.3742	7.3304	7.5503	7.7768

To solve the model AMPL programming language is used. The total water supply system cost is shown in Fig. 5.

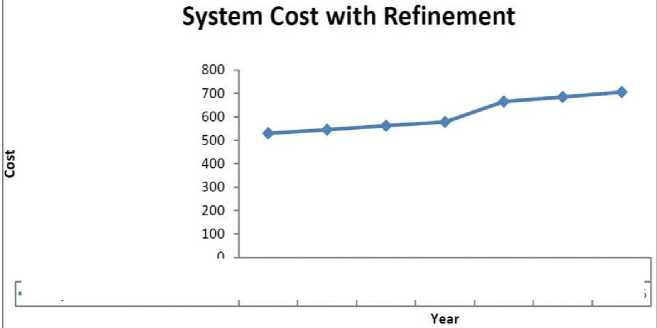
0 -	2016	2017	2018	2019	2020	2021	2022
■^^System Cost with Refinement	529.08	545.042	561393	578,236	664.972	684.92	705.466

Fig. 5. System cost with refinement

The constraint matrix of the water supply model, which takes the refining process into account, remains consistent across all cases for the years 2016 to 2022. This means that the optimal solutions for the resource variables are the same across these years, as the feasible region does not change. However, different cost coefficients yield varying optimal objective function values. Therefore, for each year's distinct cost coefficient matrix c, the formula c^T x(solution of the resource variable considering the refining process) can be utilized to determine the optimal cost of the water supply system.

• 4.2    Comparison

5.    Efficiency Calculation

The comparison between the total system cost obtained from the proposed model and that of the existing model is shown graphically in Fig.6.

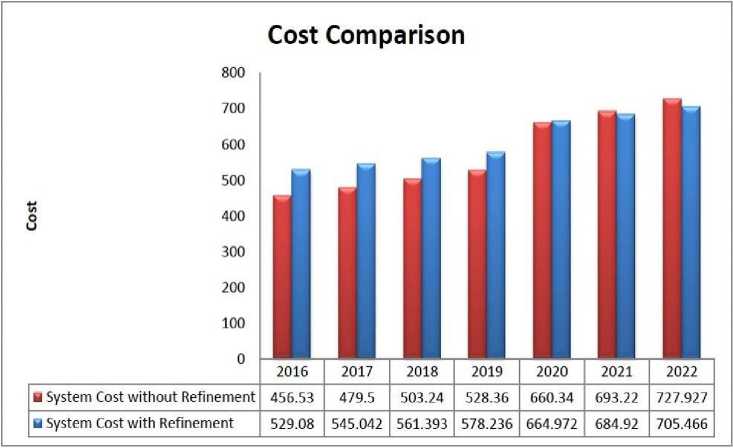
Fig. 6. Comparison between two system costs

The cost of the water supply system for the community increases gradually, both with and without the refinement step. In 2016, the cost of the system without refinement was lower than the cost with refinement. However, by 2021 and 2022, the cost without refinement surpassed the cost with refinement. Therefore, it can be concluded that the proposed water supply model offers a better long-term optimal solution for the water supply system in Dhaka city.

Two well-known stochastic measures are used to evaluate the impact of uncertainty parameters on planning decisions: the Value of the Stochastic Solution (VSS) and the Expected Value of Perfect Information (EVPI). The expected cost under uncertainty can be determined using the EVPI parameter, which is defined as follows:

EVPI = RS - WS.

Where WS refers to the objective value of the "wait and see" model and RS refers to the objective value of the two-stage stochastic recourse programming model. The WS model consists of a collection of linear programming models, each associated with a specific scenario. By weighting each scenario according to its probability, we can determine the solution to the WS model.

The potential cost of solving the two-stage stochastic recourse programming model, compared to the deterministic model, is evaluated using the VSS parameter. A positive VSS value indicates that the solutions from the stochastic programming model are better than those from the deterministic model. The VSS is defined as follows:

VSS = EEV – RS.

Where EEV stands for the deterministic models expected solution [1, 20].

In year 2016, using the proposed water supply model with refinement the recourse solution of the objective function by using 5 scenarios is RS = 529.08.

Now let us suppose that the expected value of first stage decision x is 34 then the expected solution of the objective function by using this expected value is EEV = 536.4. Using 5 scenario the Wait and See solution is

WS = 103.4256

So EVPI is 425.6544

and VSS is 7.32008

As a result, the two-stage stochastic model can yield a 1.36% higher gain compared to the deterministic model [19].

6.    Risk Aversion Optimization

Economic theory suggests that a water supply authority typically operates in a risk-averse manner, much like many other decision-makers. There are various ways to model risk aversion. One straightforward approach is to prepare for the worst-case scenario, which involves maximizing profit while minimizing costs in that scenario. It's important to note that, for some models, the scenario leading to the lowest profit may not be known in advance. However, in the proposed water supply model, the first case is identified as the worst case. Equality constraints are utilized in this model. For the year 2016, when considering a single scenario, the highest minimum cost identified is 141.816. This value is derived from the first scenario and is notably lower than the minimum cost of 529.08 from the equivalent deterministic linear programs of the stochastic water supply model. The formulation of the risk-averse optimization problem from 2016 and its refinement process is shown below:

Minz = 0x + 0.2 ^ (10у_ш - 5.83y₂ k + 5y₃ k + 11.66y_4k + 8.33y₅ k + 0y₆ k - 5.83y 7k ) k = 1

Subjectto : x - y1k + y2k = bi x — Узк + У4к + У5к = 32

x - 2y_3k + y_4k + y_5k = 0

0.9У зк — У бк — У 7к = ⁰

У 2к ⁺ У 7к = ¹⁵

wherek = 1,L ,5

^(0x + 0.2 ^ ⁽¹⁰У !к ^- 5.83У 2к ⁺ 5У зк ⁺ 11.⁶⁶У 4к ⁺ 8.33У 5к ^{+ 0}У бк — 5.8³У 7к ⁾⁾ <  z i к = 1

(Here z is the risk averse constraints bound)

0 < x < 45,0 < У1к < 36,0 < У2к < 36,0 < Узк <36,0 < У4к < 15,0 < у5к < 15,0 < Убк < 36,0 < У7к < 36, where к = 1,L , 5.

By employing risk-averse optimization, we observe that when the risk-averse constraint is set to a threshold below 529.08, the solution becomes infeasible; in other words, there is no viable region in which the cost of the water supply system can be minimized. However, when we increase the bound of the risk-averse constraints to any value above 529.08, the minimum system cost is consistently found to be 529.08. Therefore, we conclude that the system cost of the proposed water supply model, including the refining process for the year 2016, is 529.08, and the minimum water supply cost remains fixed at this value for this year.

7.    Conclusions

Human ignorance causes polluted water to mix with surface water sources. Contamination of the surface water source damages the ecosystem of the water source and increases reliance on the groundwater source. Also, the treatment cost of the surface water source gradually increases because the water source slowly becomes polluted. In this study, a scenario-based, two-stage stochastic recourse model for a water supply system with refinement is developed. The study examines the system cost of Dhaka city in Bangladesh from 2016 to 2022, excluding the refining step. However, when the refining step is included in 2016, the system cost is high. But over time, the system cost without refinement is increasing at a faster rate than the system cost with refinement, and in 2021 and 2022, the system cost with refinement is lower than the system cost without refinement. The proposed model will be very beneficial for water supply systems in Dhaka, Bangladesh, in the long run. Due to the refinement step included in the model, it is particularly relevant in today's world, where water resources are often contaminated in various ways. By refining and reusing wastewater and producing additional purified water, we can prevent the contamination of water sources. This approach will also help keep the cost of supplying drinking water from increasing significantly, ensuring that people have easier access to fresh water from reliable sources. The efficiency of the proposed SP model is shown using EVPI and VSS, and the proposed SP model is 1.36% more effective than the deterministic LP. Finally, a sensitivity analysis of the system cost is shown by using the RA optimization model. The proposed model is solved by using scenario-based, two-stage stochastic recourse problems. The proposed model is analyzed by considering seven scenarios, each with five constraints. When analyzing the model with Dhaka’s water supply system, five scenarios are considered.