Stochastic Rules in Nucleotide Sequences in Genomes of Higher and Lower Organisms

One of the founders of quantum mechanics, who introduced also the term “quantum biology,” P. Jordan noted the main difference between living and inanimate objects: inanimate objects are controlled by the average random movement of their millions of particles, whose individual influence is negligible, while in a living organism selected – genetic - molecules have a dictatorial influence on the whole living organism. Besides this, he claimed that life's missing laws were the rules of chance and probability of the quantum world [1, 2]. From the standpoint of Jordan’s statement, the study of probabilities or percentages of n -plets (monoplets, doublets, triplets, etc., that is, oligomers with lengths n) in long DNA sequences is important for discovering hidden biological laws and for developing quantum biology.

In line with this, the article describes some results of computer analysis of stochastic features of nucleotide sequences in single-stranded DNA of eukaryotic and prokaryotic genomes. Each of these genomic sequences is a long chain of 4 types of DNA nucleotides, which play the role of molecular «letters» in DNA text-like information: adenine A, cytosine C, guanine G, and thymine T. For example, the nucleotide sequence in the human chromosome №1 contains about 250 millions of the letters A, T, C, and G. As a result of the computer analysis of the percentage composition of DNA-texts of many genomes, certain probability rules were identified, which are candidates for the role of universal genetic rules. All computer programs for this analysis of genomic sequences were created by V.I.Svirin who is one of the co-authors of the article. An additional algebra-matrix presentation of the obtained data on the percentage composition of many genomic DNA reveals the conjugation of these rules with the formalisms of quantum mechanics and quantum informatics. The article aims to present and discuss new phenomenologic rules of percentage compositions in eukaryotic and prokaryotic genomes and also to enrich by new data suppositions of many authors that formalisms of quantum informatics can be effectively used for deep understanding and modeling biological bodies (see, for example [3-6]). The presented results and stochastic rules significantly expand the knowledge about stochastic regularities in genomic nucleotide sequences of single-stranded DNA, which were presented till now mainly by the second Chargaff's rule saying about phenomenological approximate equalities of percentages of nucleotides A and T (%A ≈ %T) and also C and G (%C ≈ %G) in such sequences [7-9]. The presented new rules can be considered as generalizations of the second Chargaff's rule. А literature review on the topic of stochastic features of long DNA sequences is contained in the article [10].

The article additionally shows and discusses new structural connections of molecular genetic systems with the historically famous table of 64 hexagrams from the Ancient Chinese book «I-Ching» written a few thousand years ago. These connections add materials to previously known data about structural analogies between molecular genetic systems and Yin-Yang schemes of «I-Ching», which were described, for example, in [11-14]. These new connections are also discussed in the article.

2.    Methodology

As it is known, there is a system of DNA alphabets of 4 nucleotides, 16 doublets, 64 triplets, etc. Each of such alphabets consists of 4 ⁿ elements of length n and can be considered as an alphabet of a separate text. The described study of genomes is carried out based on the original method for various reading of any DNA sequence consistently using each of the n -plets alphabets of this system. By this method, the analyzed sequence is represented as a whole set of n parallel texts (or layers), each of which is written in its own language based on one of the n different alphabets. In other words, the analyzed DNA sequence appears as a set of n texts in n different alphabets: firstly, as a text in the form of a sequence of 4 kinds of nucleotides; secondly, as a text in the form of a sequence of 16 kinds of doublets; etc. For example, in the sequence ACCTGTAACG... the first text (or layer) is based on the 4 nucleotides (A-C-C-C-T-G- ...), the second text is based on 16 doublets (AC-CT-GT-AA-CG- ...), the third text is based on 64 triplets (ACC- TGT-AAC- ..), etc. In each n ^th layer, we calculate the percentages of each of the 4 ⁿ types of n -plets and study the relationship between all of them in different layers. Using this original method to study DNA sequences in the genomes of higher and lower organisms, taken from the GenBank, the authors have discovered the existence of previously unknown stochastic regularities and symmetries in them, which are currently candidates for the role of universal genomic rules.

For comfortable showing the calculated set of phenomenological percentages of n-plets in genomic DNA layers, we use the tensor family of matrices [C, A; T, G]^{( n )} (Table 1), where the symbol ( n ) refers to the tensor power n = 1, 2, 3, 4,… . This tensor family was described in the book [13] and based on the system of binary-oppositional molecular traits in the DNA alphabet of four nucleotides C, A, T, and G:

• 1)    two of these molecules are purines with two rings (A and G), and the other two are pyrimidines with one ring (C and T). In terms of these oppositional indicators, C = T = 1, A = G = 0 ;

• 2)    the two letters are keto molecules (T and G), and the other two - amino molecules (C and A). In terms of these oppositional indicators, C = A = 1, T = G = 0.

Table.1. The tabular representation of the DNA-alphabets of 4 nucleotides, 16 doublets, 64 triplets, and 256 tetraplets. These tables are constructed by the described binary numbering of their rows and columns (see explanations in the text).

	11	10	01	00
11	сс	СА	АС	АА
10	ст	CG	АТ	AG
01	тс	ТА	GC	GA
00	тт	TG	GT	GG

	111	но	101	100	ОН	010	001	000
111	ссс	ССА	САС	САА	АСС	АСА	ААС	AAA
НО	сст	CCG	CAT	CAG	ACT	ACG	ААТ	AAG
101	СТС	СТА	CGC	CGA	АТС	АТА	AGC	AGA
100	стт	сто	CGT	CGG	АТТ	ATG	AGT	AGG
он	тсс	ТСА	ТАС	ТАА	GCC	ОСА	GAC	GAA
010	тст	TCG	ТАТ	TAG	ОСТ	GCG	GAT	GAG
001	ттс	ТТА	TGC	TGA	GTC	GTA	GGC	OGA
ООО	ттт	TTG	TGT	TGG	ОТТ	ОТО	GOT	GOG

1111

1110

1101

1100

1011

1010

1001

1000

0111

OHO

0101

0100

OOH

0010

0001

0000

1111

сссс

СССА

ССАС

ССАА

САСС

САСА

СААС

СААД

ACCC

ACCA

ACAC

ACAA

AACC

AACA

AAAC

AAAA

1110

ссст

СССС

С CAT

ССАС

едет

САСС

СААТ

СААС

ACCT

ACCC

ACAT

ACAC

AACT

AACG

AAAT

AAAC

1101

сстс

ССТА

СССС

СССА

САТС

САТА

САСС

САСА

лете

ACTA

ACGC

ACCA

AATC

ДАТА

AAGC

AAGA

1100

сстт

С СТС

CCGT

СССС

САТТ

САТС

CAGT

САСС

ACTT

ACTG

AC GT

ACCC

AATT

AATG

AACT

AAGC

1011

стсс

СТСА

СТАС

СТАД

СССС

СССА

ССАС

CGAA

ATCC

ATCA

ATAC

ATAA

AGCC

ACCA

ACAC

AGAA

1010

стст

СТСС

СТАТ

СТАС

СССТ

СССС

CGAT

CGAG

ATCT

ATCG

ATAT

ATAG

AG CT

ACCC

ACAT

ACAC

1001

сттс

СТТА

СТСС

СТСА

сстс

CGTA

СССС

CGGA

ATTC

ATTA

ATGC

ATGA

AGTC

AGTA

AGGC

AGGA

1000

сттт

CTTG

СТСТ

СТСС

CGTT

ССТС

CGGT

СССС

ATTT

ATTG

ATCT

ATGG

AGTT

ACTG

AGGT

AGGG

0111

тссс

ТССА

ТСАС

ТСАА

ТАСС

ТАСА

ТААС

TAAA

GCCC

GCCA

GCAC

GCAA

GACC

GACA

GAAC

GAAA

оно

тест

ТССС

ТСАТ

TCAG

TACT

ТАСС

ТААТ

TAAG

GCCT

GCCG

GCAT

GCAG

GACT

GACG

GAAT

GAAC

0101

тстс

ТСТА

ТССС

ТССА

ТАТС

ТАТА

ТАСС

TAGA

GCTC

GCTA

GCGC

GCGA

CATC

GATA

GACC

GAGA

0100

тстт

ТСТС

тест

ТССС

ТАТТ

ТАТС

TACT

TAGG

GCTT

GCTC

CCGT

GCCC

GATT

GATG

GACT

GAGG

ООН

ттсс

ТТСА

ТТАС

ТТАА

ТССС

ТССА

TGAC

TGAA

GTCC

GTCA

GTAC

GTAA

GGCC

GCCA

GGAC

GGAA

0010

ттст

TTCG

ТТАТ

TTAG

TGCT

ТССС

ТСАТ

TGAG

GTCT

GTCC

GTAT

GTAG

GCCT

GCCC

GCAT

GGAG

0001

тттс

ТТТА

ТТСС

TTGA

ТСТС

ТСТА

TGGC

TGGA

GTTC

GTTA

GTGC

GTCA

GCTC

GGTA

GGCC

GGGA

0000

ТТТТ

TTTG

TTGT

TTGG

тстт

TGTG

тест

TGGG

GTTT

CTTG

GTCT

GTGC

GGTT

GGTG

GGGT

GGGG

These four tables are not simple tables but they form a single tensor family of matrices: the second, the third, and the fourth tensor powers of the (2*2)-matrix [C, A; T, G] automatically give this (4*4)-matrix of 16 doublets, this (8*8)-matrix of 64 triplets, and this (16*16)-matrix of 256 tetraplets (Table 1). Using the same method of the binary numbering of rows and columns of square matrices of DNA alphabets of n -plets, one can similarly construct square tables of 1024 pentaplets, and so on. These new tables will also be members of the unified tensor family of symbolic matrices [C, A; T, G]^{( n )} for values n = 5, 6, ... Each of n -plets occupies its strong individual place in this tensor family of tables, which form a tensor family of square matrices. The connection of the DNA system of alphabets with the tensor product of matrices is interesting because this product plays an important role in quantum mechanics and quantum informatics. For example, the state space of a composite physical system is determined by the tensor product of the state spaces of its components.

By placing the percentage of each n -plet (calculated inside the n ^th layer of given DNA-text) into the cell occupied by this n -plet in the appropriate square matrix, we obtain the numerical matrices of probabilities of all n -plets inside the n ^th layer of given DNA-text. Analysis of this family of probability matrices for n -plets reveals hidden regularities in the structural organization of the studied genomic DNA-texts. Below these regularities for n = 1, 2, 3, 4 are described and discussed taking into account formalisms of quantum mechanics and quantum informatics.

For computer analysis, nucleotide sequences in single-stranded DNA of eukaryotic and prokaryotic genomes from the well-known Genbank are used. By computer programs, in each of the studied layers of a genomic DNA, an individual quantity of each kind of n-plets is calculated; then this quantity is divided by the total amount of all n-plets in this layer to define a percent of this kind of the n-plets in the layer. One can remind that genomic sequences in the GenBank sites usually contain some letters N, which indicate that there can be any nucleotide in this place . For this reason, the total amount of all nucleotides A, T, C, G, which are calculated for the sequence from the GenBank, is slightly less than the complete length of the DNA sequence, which is indicated in the GenBank. But practically this is not essential for the resulting values of percentages of separate nucleotides in the analyzed genomic sequences.

It is comfortable to explain our general results using a particular example of the DNA of the human chromosome №1, which contains a sequence of about 250 million nucleotides C, A, T, and G (initial data on this chromosome were taken in the GenBank: .

At the first step of the analysis, the percents of each of the nucleotides C, A, T, and G in this chromosome are calculated: %C ≈ 0.2085, %G ≈ 0.2089, %A ≈ 0.2910, %T ≈ 0.2917 (here percents are shown in fractions of one). Here and below, percentages are usually rounded to the fourth decimal place. These percent values are used to be indicated in appropriate cells of the matrix of nucleotides [C, A; T, G] instead of nucleotide symbols for receiving a numeric matrix of nucleotides percents [Table 2, upper row]. One can note that %C ≈ %G and %A ≈ %T in line with the second Chargaff's rule [7-9].

Table 2. The transformation of the symbolic matrices of 4 nucleotides and 16 doublets from Table 1 into appropriate numeric matrices of percent of nucleotides and doublets in the case of the human chromosome №1.

C	A
T	G

*

%C	%A
%T	%G

0.2085	0.2910
0.2918	0.2087

%CC	%CA	%AC	%AA
%CT	%CG	%AT	%AG
%TC	%TA	%GC	%GA
%TT	%TG	%GT	%GG

0.05409	0.07274	0.05033	0.09504
0.07134	0.01031	0.07429	0.07137
0.06008	0.06312	0.04402	0.06008
0.09568	0.07286	0.05046	0.05419

At the second step of the described approach, the DNA-text of the analyzed chromosome is represented as a text of doublets (for example, the text TAACCCTA… is represented as TA-AC-CC-TA-…) and percents of each of 16 doublets are calculated. Then these percents are indicated in appropriate cells of the (4*4)-matrix [C, A; T, G](2) (Table 2, bottom row).

At the third step of the described approach, the DNA-text of the analyzed chromosome is represented as a text of triplets, and the percent of each of 64 triplets is calculated. Then these percents are indicated in appropriate cells of the (8*8)-matrix [C, A; T, G](3) (Table 3).

Table 3. The matrix of percent of the 64 triplets in the DNA-sequence of triplets in the human chromosome №1.

%CCC	%CCA	%CAC	%CAA	%ACC	%ACA	%AAC	%AAA
%CCT	%CCG	%CAT	%CAG	%ACT	%ACG	%AAT	%AAG
%CTC	%CTA	%CGC	%CGA	%ATC	%ATA	%AGC	%AGA
%CTT	%CTG	%CGT	%CGG	%ATT	%ATG	%AGT	%AGG
%TCC	%TCA	%TAC	%TAA	%GCC	%GCA	%GAC	%GAA
%TCT	%TCG	%TAT	%TAG	%GCT	%GCG	%GAT	%GAG
%TTC	%TTA	%TGC	%TGA	%GTC	%GTA	%GGC	%GGA
%TTT	%TTG	%TGT	%TGG	%GTT	%GTG	%GGT	%GGG

0.0138	0.0188	0.0152	0.0186	0.0118	0.0198	0.0145	0.0369
0.0185	0.0029	0.0179	0.0210	0.0162	0.0025	0.0238	0.0199
0.0176	0.0127	0.0025	0.0023	0.0132	0.0194	0.0144	0.0224
0.0201	0.0209	0.0026	0.0029	0.0239	0.0178	0.0161	0.0185
0.0159	0.0196	0.0110	0.0199	0.0125	0.0146	0.0096	0.0196
0.0223	0.0023	0.0194	0.0128	0.0144	0.0025	0.0133	0.0176
0.0197	0.0198	0.0146	0.0195	0.0096	0.0112	0.0126	0.0160
0.0372	0.0188	0.0199	0.0190	0.0145	0.0153	0.0119	0.0138

At the fourth step of the described approach, the DNA-text of the analyzed chromosome is represented as a text of tetraplets (such as TAAC-CCTA-…) and percents of each of 256 tetraplets are calculated. Then these percents are indicated in appropriate cells of the (16*16)-matrix [C, A; T, G](4) shown in Table 1. The resulting matrix of percent of 256 tetraplets is presented in Table 4.

Table 4. The matrix of percents of the 256 tetraplets in the DNA-sequence of tetraplets in the human chromosome №1.

.0033	.0055	.0042	.0044	.0040	.0056	.0032	.0070	.0030	.0042	.0040	.0053	.0032	.0059	.0055	.0149
.0041	.0010	.0044	.0058	.0047	.0010	.0040	.0044	.0041	.0005	.0051	.0054	.0047	.0006	.0095	.0071
.0050	.0029	.0008	.0006	.0036	.0039	.0049	.0059	.0037	.0032	.0006	.0006	.0040	.0070	.0037	.0066
.0048	.0058	.0006	.0009	.0057	.0047	.0045	.0058	.0049	.0044	.0007	.0007	.0071	.0057	.0049	.0047
.0052	.0057	.0027	.0038	.0010	.0006	.0003	.0006	.0033	.0045	.0032	.0063	.0042	.0049	.0039	.0078
.0058	.0009	.0035	.0028	.0007	.0003	.0005	.0008	.0049	.0005	.0064	.0035	.0046	.0007	.0049	.0059
.0048	.0036	.0046	.0051	.0005	.0004	.0008	.0006	.0047	.0056	.0033	.0050	.0031	.0037	.0047	.0057
.0073	.0044	.0053	.0058	.0006	.0010	.0005	.0010	.0096	.0040	.0051	.0044	.0046	.0047	.0040	.0041
.0046	.0049	.0042	.0051	.0024	.0045	.0028	.0078	.0030	.0041	.0029	.0038	.0023	.0037	.0029	.0073
.0057	.0006	.0051	.0052	.0037	.0004	.0056	.0036	.0047	.0008	.0033	.0046	.0030	.0005	.0046	.0048
.0057	.0040	.0005	.0006	.0030	.0055	.0026	.0041	.0032	.0027	.0006	.0005	.0025	.0031	.0032	.0057
.0068	.0058	.0006	.0006	.0070	.0039	.0032	.0029	.0037	.0048	.0006	.0008	.0041	.0036	.0036	.0051
.0051	.0063	.0034	.0063	.0041	.0049	.0031	.0061	.0023	.0031	.0017	.0035	.0031	.0042	.0023	.0052
.0077	.0006	.0063	.0038	.0049	.0006	.0045	.0057	.0038	.0004	.0032	.0027	.0042	.0010	.0034	.0052
.0073	.0078	.0038	.0051	.0037	.0046	.0042	.0051	.0030	.0028	.0029	.0042	.0023	.0024	.0030	.0046
.0150	.0072	.0055	.0045	.0059	.0057	.0043	.0054	.0055	.0032	.0040	.0042	.0032	.0039	.0030	.0033

At first glance, the set of percent in the resulting matrices (Tables 2-4) is quite chaotic. It has the following features regarding the percent of separate n -plets:

• •    Percent of presented n -plets significantly depends on the order of letters in them. For example, the percent of doublets CG and GC, having the same letter composition, differ several times: %CG = 0.0103 and %GC = 0.0440. Similarly, the percent of triplets of the same letter composition CAT, CTA, ACT, ATC, TCA, TAC are significantly different: %CAT=0.0179, %CTA=0.0127, %ACT=0.0162, %ATC=0.0132, %TCA=0.0196, %TAC=0.0110, and so on;

• •    Accordingly, the matrices of phenomenological percentages of doublets, triplets, and tetraplets (Tables 2-4) don’t coincide numerically with matrices of the tensor family [%C, %A; %T, %G]^{( n )} = [0.2085, 0.2910; 0.2918, 0.2087]^{( n )}.

But unexpectedly these values %C=0.2085, %G=0.2087, %A=0.2910, %T=0.2917 showed themselves in the block organization of percentages of different n -plets in various layers of the genomic DNA-text as one can calculate from data of percent matrices in Tables 2-4. For example, the following sums of percentages of n -plets, which have the nucleotide C as an attributive indicator of their grouping, are realized:

• •    The total sum Σ%CN of percentages of all 4 doublets CN (hereinafter, the symbol N denotes any of the nucleotides A, T, C, and G), which start with the nucleotide C, is equal to %C, that is, Σ%CN = %CC + %CA +%CT + %CG ≈0.0541+0.0727+0.0713+0.0103 ≈ 0.2085 ≈ %C;

• •    The total sum Σ%NC of percentages of all 4 doublets NC, which have the nucleotide C at their second positions, is practically equal to %C, that is, Σ%NC = %CC +%AC + %TC +%GC = 0.0541+0.0503+0.0601+0.0440 ≈ 0.2085 ≈ %C as well;

• •    The total sum Σ%CNN of percentages of all 16 triplets CNN, which have the nucleotide C at their first position, is practically equal to %C, that is, Σ%CNN ≈ 0.0284 ≈ %C as well;

• •    The total sum Σ%NCN of percentages of all 16 triplets NCN, which have the nucleotide C at their second position, is practically equal to %C, that is, Σ%NCN ≈ 0.0285 ≈ %C as well;

• •    The total sum Σ%NNC of percentages of all 16 triplets NNC, which have the nucleotide C at their third position, is practically equal to %C, that is, Σ%NNC ≈ 0.0285 ≈ %C as well;

• •    The total sum Σ%CNNN of percentages of all 64 tetraplets CNNN, which have the nucleotide C at their first position, is practically equal to %C, that is, Σ%CNNN ≈ 0.0285 ≈ %C as well;

• •    The total sum Σ%NCNN of percentages of all 64 tetraplets NCNN, which have the nucleotide C at their second position, is practically equal to %C, that is, Σ%NCNN ≈ 0.0285 ≈ %C as well;

• •    The total sum Σ%NNCN of percentages of all 64 tetraplets NNCN, which have the nucleotide C at their third position, is practically equal to %C, that is, Σ%NNCN ≈ 0.0285 ≈ %C as well;

• •    The total sum Σ%NNNC of percentages of all 64 tetraplets NNNC, which have the nucleotide C at their fourth position, is practically equal to %C, that is, Σ%NNCN ≈ 0.0285 ≈ %C as well.

A similar phenomenological situation holds for other nucleotides G, A, T as attributive indicators of appropriate groupings of n -plets. Table 5 shows this stochastic phenomenon of the constant values of sums of percentages of appropriate n -plets in n -plets layers of the DNA-text of the human chromosome №1.

Table 5. Percentages of nucleotides C, G, A, T, and the sum Σ of percent of n -plets with these nucleotides at their certain positions for the first 4 layers in the DNA-text of the human chromosome №1 (here n = 1, 2, 3, 4). The symbol N denotes any of the nucleotides.

%C ≈ 0.2085	%G ≈ 0.2087	%A ≈ 0.2910	%T ≈ 0.2918
Σ%CN ≈ 0.2085	Σ%GN ≈ 0.2088	Σ%AN ≈ 0.2910	Σ%TN ≈ 0.2917
Σ%NC ≈ 0.2085	Σ%NG ≈ 0.2087	Σ%NA ≈ 0.2910	Σ%NT ≈ 0.2918
Σ%CNN ≈ 0.2084	Σ%GNN ≈ 0.2088	Σ%ANN ≈ 0.2910	Σ%TNN ≈ 0.2917
Σ%NCN ≈ 0.2085	Σ%NGN ≈ 0.2088	Σ%NAN ≈ 0.2910	Σ%NTN ≈ 0.2917
Σ%NNC ≈ 0.2085	Σ%NNG ≈ 0.2087	Σ%NNA ≈ 0.2910	Σ%NNT ≈ 0.2918
Σ%CNNN ≈ 0.2085	Σ%GNNN ≈ 0.2088	Σ%ANNN ≈ 0.2910	Σ%TNNN ≈ 0.2917
Σ%NCNN ≈ 0.2085	Σ%NGNN ≈ 0.2087	Σ%NANN ≈ 0.2910	Σ%NTNN ≈ 0.2918
Σ%NNCN ≈ 0.2085	Σ%NNGN ≈ 0.2088	Σ%NNAN ≈ 0.2910	Σ%NNTN ≈ 0.2918
Σ%NNNC ≈ 0.2085	Σ%NNNG ≈ 0.2087	Σ%NNNA ≈ 0.2910	Σ%NNNT ≈ 0.2918

Briefly speaking, the following equalities (1) hold - with a high level of accuracy - regarding percentages of the nucleotides C, G, A, and T, and the considered 4 groupings of n -plets in the human chromosome №1:

%C ≈ Σ%CN ≈ Σ%NC ≈ Σ%CNN ≈ Σ%NCN ≈ Σ%NNC ≈ Σ%CNNN ≈ Σ%NCNN ≈ Σ%NNCN ≈ Σ%NNNC;

%G ≈ Σ%GN ≈ Σ%NG ≈ Σ%GNN ≈ Σ%NGN ≈ Σ%NNG ≈ Σ%GNNN ≈ Σ%NGNN ≈ Σ%NNGN ≈ Σ%NNNG;

%A ≈ Σ%AN ≈ Σ%NA ≈ Σ%ANN ≈ Σ%NAN ≈ Σ%NNA ≈ Σ%ANNN ≈ Σ%NANN ≈ Σ%NNAN ≈ Σ%NNNA;

%T ≈ Σ%TN ≈ Σ%NT ≈ Σ%TNN ≈ Σ%NTN ≈ Σ%NNT ≈ Σ%TNNN ≈ Σ%NTNN ≈ Σ%NNTN ≈ Σ%NNNT

Knowing the percentages of nucleotides %A, %T, %C, and %G, it is possible to predict with high accuracy the sums of percentages of n -plets of the noted groupings. The ability of such predictions based on equalities (1) holds not only for the considered human chromosome №1 but also for many eukaryotic and prokaryotic genomes, which were analyzed by the till now including the following:

• 1)    all 24 human chromosomes, which differ in their length, the number, and type of genes, etc.;

• 2)    all chromosomes of a fruit fly Drosophila melanogaster , all chromosomes of a house mouse Mus musculus , all chromosomes of a nematode Caenorhabditis elegans , all chromosomes of a plant Arabidopsis thaliana , and many other plants;

• 3)   19 bacterial genomes of different groups both from Bacteria and Archaea.

One should add that percentages of nucleotides %A, %T, %C, and %G can be essentially different in various genomes.    For    example,    in    the    genome    of    bacteria    Bradyrhizobium    japonicum where %A≈0.1819, %T≈0.1815, %C≈0.3184, and %G≈0.3182 in contrast to the considered case of the human chromosome №1.

The four columns in Table 5 show that in each of the presented layers of the genomic DNA-text, there exist corresponding tetra-groupings of n -plets with the same percentage sums. The following rule of probabilities can be formulated based on such results:

• • All n layers of a long DNA-text, each of which consists of a sequence of 4 ⁿ n -plets, has approximately the same sum of percentages of all those n -plets, which contain the considered nucleotide (C, G, A, or T) at a fixed m th position ( m ≤ n ); here n = 1, 2, 3, 4, ... but is not too large compared to the length of DNA.

By this rule, the percentage sums of n -plets in such groupings in different layers of a considered long DNA-text are equal to the percentage of a corresponding nucleotide in the first layer of the DNA-text, although the percent values of individual n -plets, that are summands in these sums, can differ significantly. For example, in the second layer of the DNA-text of the human chromosome № 1, the sum of the percentages of all 4 doublets with nucleotide C in their first position ( m = 1) is equal to Σ%CN ≈ %CC+%CA+%CT+%CG ≈ 0.0541 + 0.0727 + 0.0713 + 0.0103 ≈ 0.2085. In the same second layer, the sum of the percentages of all 4 doublets with a nucleotide C in the second position ( m = 2) is equal to the same number, although the summands in this sum are significantly different: Σ%NC = %CC+%AC+%TC+%GC = 0.0541 + 0.0503 + 0.0601 + 0.0440 ≈ 0.2085. These two equal total values are equal to the percentage of nucleotide C in the first layer of the given genomic DNA-text: %C ≈ 0.0285.

Each of the tetra-groupings of n -plets, which is defined by a disposition of attributive nucleotides C, G, A, and T at a certain position m ( m ≤ n ) in these n -plets, we call an m -positional tetra-grouping. For example, a tetra-grouping corresponding to sets ANN, TNN, CNN, and GNN is called as a 1-positional tetra-grouping; a tetra-grouping corresponding to NAN, NTN, NCN, NGN is called a 2-positional tetra-grouping, and so on. The described stochastic phenomena have some analogies with the phenomena of holography, in which it is possible to reconstruct the image of a whole object from the image of its piece. Indeed, the knowledge of the sums of the percentages of n -plets in m -positional tetra-groupings of one layer of a long DNA-text gives knowledge about the sums of the percentages of n -plets in m -positional tetra-groupings of other layers.

Similar phenomenological results were also received regarding percentages of n -plets in special subsequences of long nucleotide sequences in single-stranded DNA. These subsequences are termed «DNA epi-chains» [15-18]. Our initial results testify that the above-described equalities (1) of total sums of percentages of n -plets hold for these epichains as well. By definition, in a nucleotide sequence N₁ of any DNA strand with sequentially numbered nucleotides 1, 2, 3, 4, ... (Fig. 1a), epi-chains of different orders k are such subsequences that contain only those nucleotides, whose numeration differ from each other by natural number k = 1, 2, 3, 4, … For example, in any single-stranded DNA, one can consider its epi-chain of the second-order N₂, in which its nucleotide sequence numbers differ by k = 2: an epi-chain N₂ contains nucleotides with numerations 1, 3, 5, … (Fig. 1b). By analogy, an epi-chain of the third-order N₃ is connected with k =3 and contains a subsequence of nucleotides with numerations 1, 4, 7, 10, ... (Fig. 1c).

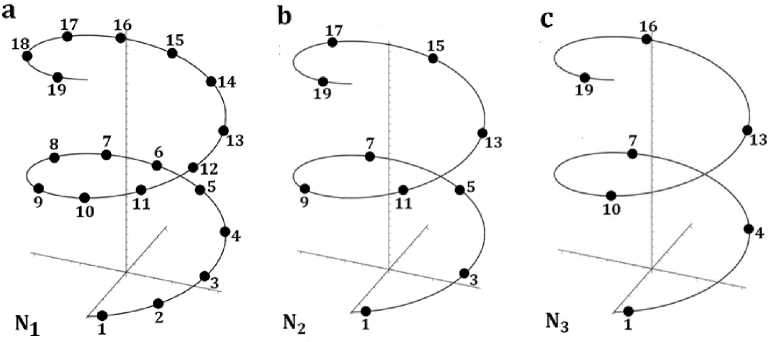
Fig. 1. Schematic representations of a single-stranded DNA and its initial epi-chains of numerated nucleotides, denoted by black circles. a, a sequence N₁ of numerated nucleotides of the DNA strand; b, an epi-chain of the second- order N 2 having nucleotides with numbers 1-3-5-?-...; c, an epi-chain of the third-order N₃ nucleotides numbers 1-4-7-10-....

The rule of the constancy of the sums of percentages in the different layers of long DNA-texts (in the indicated tetra-groupings of n -plets), which is relatively independent of the percent values of separate n -plets, the authors call as the Gestalt genetic rule of percentages of n -plets for their C-, G-, A-, and T-groupings in multilayer DNA-texts of genomes. The names "Gestalt genetic phenomena" and "Gestalt genetic rules" are due to a similarity of these genetic phenomena with the phenomena of Gestalt psychology. In Gestalt psychology literature, the term "Gestalt" is traditionally capitalized; due to this tradition, we also capitalize this term in the name "Gestalt genetics".

The discovered and described genomic phenomena of the relative independence of the sums of the percentages of n -plets (in the indicated tetra-groupings) from the values of individual percentages in these sums resemble the phenomenon of perceiving a musical melody: a musical melody can be reproduced by different musical instruments and in different frequency ranges, that is, under significantly changing the frequency of the sound of each of its note elements, but despite these changes, the melody remains generally recognizable.

Many such phenomena of perception, in which there is relative independence of the integral form from its constituent individual components, are studied in Gestalt psychology. The phenomena of perception of visual, auditory, and other images, studied by Gestalt psychology, reflect the fundamental inherited property of the psyche - to seek in a disparate whole. Thanks to the ability to think in Gestalts, you can understand the sentence, even if you change the order of the letters in each word and leave only the beginning and end in place.

The described universal regularities in the preservation of total percentages in tetra-groupings of n -plets relatively regardless of the percentage of individual n -plets in genomic multilayer DNA-texts allow the authors to develop Gestalt genetics. This scientific direction studies holistic genetic patterns that are relatively independent of particular components. It seems natural to think that Gestalt genetics is interrelated with Gestalt psychology, which studies some genetically inherited properties of our brain regarding the perception of the environment.

Gestalt genetics comes in contact with the teachings of the creator of analytical psychology C. Jung and his associate Nobel laureate in physics W. Pauli about the archetypes of the unconscious; in particular, they linked these archetypes with the Yin-Yang schemes of the ancient Chinese book "I-Ching" and its table of 64 hexagrams, which have deep structural analogies with the DNA alphabets (these analogies were noted by some reputable geneticists - G.S. Stent in 1969, and Nobel laureate F. Jacob in 1977; extended information on these analogies is in publications [11, 12, 13, 19]).

In our opinion, the origins of the genetically inherited ability of the brain to work with Gestalt images should be sought in Gestalt genetics. In particular, Gestalt genetics is capable of providing new approaches to understanding the noise immunity of genetic information under mutations of DNA-texts.

In addition to the phenomena of Gestalt psychology, in living organisms, there are many genetically inherited physiological phenomena, in which the same whole pattern is realized in conditions of a wide variety of constituent elements and which can be attributed to Gestalt biology (this new name is proposed as uniting genetically inherited Gestalt-like phenomena of different types). For example, Gestalt biology includes some genetically inherited phenomena of morphogenesis (laws of phyllotaxis, spiralization of biological structures at various levels and branches of biological evolution), as well as some functional phenomena (homeostasis at different stages of ontogenesis; the processing of sensory information from different sense organs according to main psychophysical law of Weber-Fechner; the biomechanical phenomenon, known as Bernstein's problem, that the general target task of body movement is performed exactly regardless of the inaccuracies of its constituent motor subtasks). The authors think that various genetically inherited phenomena of Gestalt biology are based on Gestalt genetics.

One should also recall that the molecular composition of a living body is constantly changing while maintaining the shape of the body. Our body's proteins are involved in continuous life-death cycles of their assembling and disassembling into amino acids. For example, the half-life of the hormone insulin is 6-9 minutes, etc. In other words, genetically inherited parts of our body are constantly dying and reborn. Taking into account such phenomena, the renowned physiologist A.G. Gurvich claimes: " The main problem in biology is maintaining shape while constantly renewing the substrate " [20]. In our opinion, the described phenomena of Gestalt genetics with its Gestalt rules of percentages in genomic multilayer DNA-texts are directly related to this fundamental problem of biology.

The genetic coding system has binary-oppositional structures at different levels of its organization. As it is known, the ancient Chinese book I-Ching, which was written a few thousand years ago, has introduced the system of symbols Yin and Yang (equivalents of 0 and 1). This book had a powerful impact on the culture, medicine, and science of ancient China and several other countries. The system of I-Ching is represented by the schemes with 4 bigrams, 8 trigrams, and 64 hexagrams. Similar to this, the genetic code is constructed on DNA molecules using 4 nitrogenous bases, 16 doublets, and 64 triplets. Structural analogies of Yin-Yang schemes of I-Ching with the alphabets of DNA have long been noted by various authors (see some details in [11, 12, 13, 19]).

A great number of literature sources are devoted to I-Ching. Many of these sources label I-Ching as one of the greatest and most mysterious human creations. From the viewpoint of the Chinese culture (the most ancient among all cultures, which continue their existence on the Earth), I-Ching represents something even more considerable: the creation made by the Superperson, who embodied a secret of the Universe in special symbols and signs. This book has a fundamental paradigmatic influence on the whole culture of traditional China and the adjacent countries. The ideas expressed in it have created an original world-view and methodology. The symbols and principles of I-Ching penetrated all spheres of life of traditional China from theoretical conceptions and high art to household subjects and decorations. Confucius said: “ If it would be possible to extend my years, I would have given fifty of them for the study of I-Ching “ [21]. I-Ching declares a universality of the cyclic principle of organization in nature. Traditional Oriental medicine is based on the viewpoints of this book.

Many western scientists studied and used I-Ching. For example, the creator of analytical psychology C. Jung developed his doctrine about the collective unconscious in connection with this book. According to him, the trigrams and the hexagrams of I-Ching “ fix a universal set of archetypes (innate psychic structures) ” [21, p. 12]. Niels Bohr chose the Yin-Yang symbol as his personal emblem. Many modern physicists, who feel the unity of the world, connect their theories with the ideas of traditional Oriental culture, which unite all nature. The intensive development of the selforganizing and nonlinear dynamics of complex systems (synergetics) promotes the strengthening attention of western scientists to the traditional eastern world-view (e.g., see [22]).

Table 6. The table of 64 hexagrams in Fu-Xi's order from I-Ching where each of hexagrams is shown in the symbolic Chinese tradition and also in a binary representation: each solid or broken line corresponds to 1 or 0 correspondingly. Chinese names of trigrams are also shown.

	111 CHYAN	no TUI	101 LI	100 CHEN	on HSUN	010 KAN	001 KEN		000 KUN
Ill CH VAN	mm	ILLI 10	11ШН	111100	1110 n	тою		1100 1	111000
no TUI	11011 1	110110	11010 1	110100	11001 1	110010		L10001	110000
LI	min i	mn io	mno i	mnoo	10101 1	mmio	101001		miooo
100 CHEN	10011 1	100110	10010 1	100100	10001 1	100010		10000 1	100000
HSUN	oiiii i	011110	01110 1	011100	01101 1	011010		Ш00 1	011000
010 KAN	01011 1	010110	01010 1	010100	01001 1	010010		01000 1	010000
001 KEN	Oglll l	001110	0Q110 1	001100	00101 1	001010		10100 1	001000
ООО KUN	Ogglll	000110	0Q0101	000100	000011	000010		100001	000000

According to Ancient Chinese, “ trigrams, hexagrams and their components in all possible combinatory combinations form a universal hierarchy of classification schemes. These schemes in visual patterns embrace any aspects of reality - spatial parts, time intervals, the elements, numbers, colors, body organs, social and family conditions, etc .” [21, p. 10]. The Ancient Chinese claimed that the table of 64 hexagrams (Table 6) is the universal archetype of nature. The Ancient Chinese knew nothing about the genetic code, but the genetic code is arranged following the I-Ching in many aspects. One can see deep structural analogies between the genetic matrix of 64 triplets (Table 1) and the ancient table of 64 hexagrams (Table 6).

Each hexagram is a pile of six broken and unbroken (solid) lines. According to the western tradition, these broken and unbroken lines are shown in the form of the binary symbols “0” and “1” and each hexagram represents a sequence of such six binary symbols. Table 6 demonstrates hexagrams in both of these forms. Each position in all hexagrams has its number: in the western numeric presentation of a hexagram, positions of its binary symbols are numbered left-to-right by the numbers from 1 to 6; in the Chinese graphical presentation, the numbering of the lines of each hexagram is read in the sequence bottom-up.

In the table of 64 hexagrams (Table 6), 8 trigrams (three-digit binary numbers or piles of three lines) indicate its rows and columns. Each of the hexagrams is a concatenation of 2 trigrams: the trigram numerating its row and the trigram numerating its column. It should be emphasized that exactly according to a similar scheme of column and row numbering by ternary digital symbols, the (8*8)-matrix of 64 triplets of the genetic code in Table 1 is created. By this analogy, each of the 64 genetic triplets in Table 1 can be denoted by a 6-bit binary number; for example, the triplet CAC is denoted by 111101 [11]. The traditional Chinese point of view is the following: “ Hexagrams are not trigrams, which are alloyed together, but they are two trigrams, which are located on a vertical one over another ” [21, p. 101].

Now let us briefly describe some new analogies between the matrix [C, A; T, G]⁽³⁾ (Table 1) of 64 triplets, which are distributed among three different m -positional C-, G-, A-, and G-groupings (here m = 1, 2, 3), and the table of 64 hexagrams (Table 6). A key element for identifying these analogies is the following ancient Chinese doctrine about the important role of pairs of the correlative positions 1-4, 2-5, and 2-6 in Chinese hexagrams: “ The theory of I-Ching considers that a bottom trigram concerns an internal life… and a top trigram concerns to an external world…. Similar positions in a top trigram and in a bottom trigram have the nearest relation to each other. Because of this, the first position relates by analogy to the fourth position, the second position – to the fifth position, and the third position relates by analogy to the sixth position…. If these correlative positions (1-4, 2-5, 3-6) are occupied by various lines, it is considered that “conformity exists” between them, and in the case when these correlative positions are occupied by identical lines, it is considered that “conformity is absent” between them " [21, p. 86].

Tables 7-9 show the table of 64 hexagrams (Table 6) with European denotations of the hexagrams by binary numbers and with additional denotations. Pairs of binary digits that are in hexagrams at correlative positions 1-4, 2-5, and 3-6 are highlighted in 4 colors: blue color corresponds to a pair of digits 1 and 1; red color corresponds to a pair of numbers 1 and 0; yellow corresponds to a pair of digits 0 and 1; green corresponds to a pair of numbers 0 and 0. These 4 pairs of digits, standing in the mentioned positions, define appropriate tetra-groupings of 64 hexagrams, which are called the 1-positional tetra-grouping of hexagrams (it relates to the correlative positions 1-4), the 2-positional tetragrouping (it relates to the correlative positions 2-5), and the 3-positional tetra-grouping (it relates to the correlative positions 3-6).

In addition to the table of 64 hexagrams with color marks, Tables 7-9 show also matrix arrangements of triplets, which belong to the described C-, G-, A-, and G-groupings in the case of the 1-positional tetra-grouping (Table 7), in the case of the 2-positional tetra-grouping (Table 8), and in the case of the 3-positional tetra-grouping (Table 9). The following symbolic notations for each of the genetic n -plets are used for a comfortable visualization in these cases:

• -    n -plets from the C-groupings (that is, from the first column in Table 5) are denoted by the symbol ;

• -    n -plets from the G-groupings (that is, from the second column in Table 5) are denoted by the symbol 4» ;

• -    n -plets from the A-groupings (that is, from the third column in Table 5) are denoted by the symbol V;

• -    n -plets form the T-grouping (that is, from the fourth column) are denoted by the symbol .

One can see in Tables 7-9 that the arrangement of the 4 colors at correlative positions (1-4, 2-5, and 3-6) in the 64

•        •                 •                                                                                                                                                                                          •                                                             •                      • hexagrams completely coincide with the arrangement of the 4 symbols 9 ,  ,   , and in the shown genetic matrices of 64 triplets, which are connected with the described genomic Gestalt phenomena of probabilities. More precisely, in all these mutually corresponding m-positional tetra-groupings of 64 triplets and 64 hexagrams, the symbol ♦ corresponds to the hexagram pair of digits 1 and 1; the symbol V corresponds to the hexagram pair of digits 1 and 0; the symbol ♦corresponds to the hexagram pair of digits 0 and 1; the symbol 4» corresponds to the hexagram pair of digits 0 and 0.

Table 7. Identity between the arrangements of the C-, G-, A-, and T-groupings of triplets in the case of the 1-positional tetra-grouping of 64 triplets in the genetic matrix [C, A; T, G](3) from Table 1, and the arrangements of 4 groupings in the 1-positional tetra-grouping of 64 hexagrams in the ancient Chinese table of I-Ching; this tetra-grouping is defined by four binary pairs (1 and 1, 1 and 0, 0 and 1, 0 and 0) standing inside hexagrams in the traditional correlative positions 1-4. Each of the 4 groupings of hexagrams is marked by its own color (see explanations in the text).

пгзпгзоооа ПППГЗОООа ElMtltlLJLJLJLJ nrTTlUUULJ [кххшннп гзгзгзгзмммм tit It It Itlt IMtl Г1Г1ГЗГ1ММММ

111111	111110	111101	111100		11	11	111	10		111	01		111	00
110111	110110	110101	110100		10	11	|10	10		110	01		Ю	00
101111	101110	101101	101100		01	11	|01	10		101	01		101	00
100111	100110	100101	100100		00	11	100	10		100	01		100	00
011111	011110	011101	011100		Bl 1011		011010			011001			011000
010111 001111	010110 001110	010101 001101	010100 001100		010011 901011		010010 001010			010001 001001			010000 001000
000111	000110	000101	000100		900011		000010			000001			oooooo

Table 8. Identity between the arrangements of the C-, G-, A-, and T-groupings of triplets in the case of the 2-positional tetra-grouping of 64 triplets in the genetic matrix [C, A; T, G](3) from Table 1, and the arrangements of 4 groupings in the 2-positional tetra-grouping of 64 hexagrams in the ancient Chinese table of I-Ching; this tetra-grouping is defined by four binary pairs (1 and 1, 1 and 0, 0 and 1, 0 and 0) standing inside hexagrams in the traditional correlative positions 2-5. Each of the 4 groupings of hexagrams is marked by its own color (see explanations in the text).

111111	111110	1		01	1111	|o	111011	111010	111001	111000
110111	110110	1	|01	01	l|01	DO	110011	110010	110001	110000
101111	101110	1	01101		101100		101011	101010	101001	101000
100111	100110	1	00101		100100		100011	100010	100001	100000
011111	011110	0	111	01	0111	|o	011011	011010	011001	011000
010111	010110	0|01		01	0|01	Ю	010011	010010	010001	010000
001111	001110	001101			001100		001011	001010	001001	001000
000111	000110	000101			000100		000011	000010	000001	oooooo

Table 9. Identity between the arrangements of the C-, G-, A-, and T-groupings of triplets in the case of the 3-positional tetra-grouping of 64 triplets in the genetic matrix [C, A; T, G](3) from Table 1, and the arrangements of 4 groupings in the 3-positional tetra-grouping of 64 hexagrams in the ancient Chinese table of I-Ching; this tetra-grouping is defined by four binary pairs (1 and 1, 1 and 0, 0 and 1, 0 and 0) standing inside hexagrams in the traditional correlative positions 3-6. Each of the 4 groupings of hexagrams is marked by its own color (see explanations in the text).

111111	111111	111101	111100		111011	111011	г	111001	11,1000
110111	110110	110101	110100		110011	HOOK		110001	110000
101111	ЮЦЦ	101101	101100		101011	101011	1	101001	101000
100111	100110	100101	100100		100011	1000K		100001	100000
011111	011110	011101	011100	■	011011	011011	г	011001	01,1000
010111	010110	010101	010100		010011	0100K		010001	010000
001111	0011 10	001101	00,1100		001011	00^011	1	001001	001000
000111	000110	000101	000100		000011	0000 к		000001	oooooo

The parallels, which are shown in Tables 7-9, give pieces of evidence that the discovered genomic Gestalt phenomena of probabilities are structurally connected with the Yin-Yang schemes of I-Ching including the table of 64 hexagrams. Here it can be again recalled that a creator of analytical psychology C.Jung and his fellow campaigner Nobel laureate in physics W. Pauli, who were experts regarding I-Ching, believed that the trigrams and the hexagrams of I-Ching “ fix a universal set of archetypes (innate psychic structures)” [21, p. 12]. Correspondingly all these data confirm in particular that the discovered genetic Gestalt phenomena and the described genetic Gestalt rules have deep relations to properties of genetically inherited psychological phenomena and a rich theme of nature's archetypes.

I-Ching is also called the "Book of Cyclical Changes". There is a connection between various ensembles of binary numbers in the table of 64 hexagrams based on the logical operation of modulo-2 addition. For example, ensembles of binary numbers from different parts of the tetra-grouping indicated in Table 7 can be transformed into each other based on this logical operation. In particular, those two ensembles of binary numbers of the table 64 hexagrams, whose locations correspond to the location of the symbols * and ♦ in the mosaic matrix, which represents the 1-positional tetra-grouping of 64 genetic triplets in Table 7 are transformed into each other by the logical operation of modulo-2 addition of the binary number 100000 with members of the ensembles. The study of cyclical binary relationships between various tetra-groupings in matrices representing genetic Gestalt phenomena is a separate interesting topic.

4. Conclusions

The presented results of the study of the regularities in the distribution of the percentages of n -plets in different layers of composite DNA-texts of various genomes are consistent with Jordan's claiming that life's missing laws are the rules of chance and probability of the quantum world [1, 2]. The described results show the existence of previously unknown genetic regularities. These results were obtained based on new methods of analysis and modeling of DNA-texts, which are connected with mathematical formalisms of quantum mechanics and quantum informatics, algebras of multi-dimensional hypercomplex numbers, metric analysis, and the theory on noise-immune coding of informatics [11, 12, 15-18].

Considering the views of Jordan and Schrödinger about the dictatorial role of the structured informatics of genetic molecules for the whole organism [2], it is natural to think that the structural features of DNA informatics leave their marks on all genetically inherited biological systems and phenomena. This is consistent with the fact that all physiological systems must be structurally aligned with genetic coding to be transmitted in genetically encoded form to offspring. This is also consistent with the point of view that the main task of living organisms is to transfer genetic information along the chain of generations. The described algebraic-genetic results give pieces of evidence that the system of genetic coding is based on methods of probability coding, which are studied now in our laboratory. These results can be used in particular in developing model approaches presented in [23-27].

E.Schrodinger noted: “ from all, we have learned about the structure of living matter, we must be prepared to find it working in a manner that cannot be reduced to the ordinary laws of physics… because the construction is different from anything we have yet tested in the physical laboratory » [28]. For comparison, the enzymes in biological organisms work a million times more effectively than catalysts in the laboratory. What makes the enzyme in the body for 1 second, a catalyst in the laboratory can make only for 100 thousand years. We believe that such ultra-efficiency of enzymes in biological bodies is defined not only by laws of physics, but also by quantum-logical relations in the genetic system, and therefore - in line with Schrodinger - this ultra-efficiency cannot be reduced to the ordinary laws of physics. As far as we understand, the found Gestalt rules of "dictatorial" DNA-texts are not derived from the known laws of physics, and therefore refer to the special laws of the structuring of living things that Schrödinger spoke about.

The results presented in the article on the relationship between the tensor product (Table 1) and the statistical rules of DNA sequences in genomes are important for further understanding the relationship between the genetic system and the principles of quantum informatics. It may be recalled here that the very concept of a quantum computer was introduced by the founder of quantum informatics Yu.I. Manin in his book [29, p. 15] precisely when analyzing the features of high-speed processing of DNA information in chromosomes by " genetic automata ". At the same time, he assumed that the model for processing genetic information should use the division of the system into subsystems precisely on the basis of the " decomposition of space into a tensor product ". The results presented in the article confirm the correctness of this prediction, as well as the validity of considering the genetic system from the standpoint of quantum informatics. They agree with the assumptions of many authors, expressed in subsequent years, that a living organism functions on the principles of a quantum computer [3-6].

The received results can be used, in particular, for developing our knowledge about connections of genetic structures with principles of brain activities and other genetically inherited physiological systems. In general, the presented results of our studies of the structural rules of genetic informatics give pieces of evidence in favor of the effectivity of a model approach to living organisms as stochastic algebra-harmonic essences.