Стохастическая модель энергоэффективного управления вычислительной нагрузкой в многопроцессорных системах

Одним из путей решения задачи снижения энергоемкости функционирования многопроцессорных вычислительных систем (далее – МПВС) является управление вычислительной нагрузкой на каждом процессоре [1]. В основе такого управления лежит принцип использования энергосберегающих состояний на время отсутствия вычислительных задач и связанных с этим вынужденных простоев [2; 3]. При этом традиционно рассматривается детерминированная модель вычислений, предполагающая строгое соответствие организации обработки информации с заранее известными моментами завершения каждой задачи плану вычислительного процесса.

Однако наличие вероятности локальных прерываний задачами более высокого приоритета приводит к увеличению количества вынужденных простоев процессоров и неопределенности времени завершения каждой задачи. Если учесть этот фактор при организации управления вычислениями в МПВС, то можно получить дополнительный энергосберегающий эффект.

Решение задачи энергоэффективного управления стохастическими вычислительными процессами

Особенностью стохастического вычислительного процесса является отсутствие априорно известных моментов времени начала и завершения выполнения заданий. В данном случае известен лишь порядок следования заданий на каждом процессоре (ядре). В свя-

Шульгин Альберт Николаевич кандидат технических наук, преподаватель кафедры информационно-вычислительных систем и сетей, Военно-космическая академия имени А.Ф. Можайского, Санкт-Петербург. Сфера научных интересов: информационные технологии, повышение эффективности высокопроизводительных вычислительных систем, высокопроизводительные вычислительные системы. Автор более 30 опубликованных научных работ.

зи с этим при возникновении события, связанного с завершением какой-либо вычислительной задачи, встает необходимость анализа готовности очередного задания к выполнению [2; 3]. Это значит, что при связности графа параллельного алгоритма, то есть при наличии связей предшествования и последования между выполняемыми заданиями при распределенных вычислениях в МПВС [4], решение задачи энергосбережения сводится к использованию вероятностных методов расчета:

• •    моментов времени завершения выполнения заданий Z ₁, Z ₂,…, Z _n, являющихся непосредственными предшественниками для очередного задания Z _n+1;

• •    момента времени t ^ˆ _i начала выполнения очередного задания Z _n+1;

• •    параметров состояний пониженного энергопотребления процессоров (ядер) ( С -состояний) в периодах простоев различной длительности и моментах времени начала их перехода в активный режим.

На Рисунке 1 показана временная диаграмма фрагмента выполнения n вычислительных задач на m процессорах при наличии случайного прерывания одной из задач.

Так как моменты времени завершения выполнения задач-предшественников рассматриваются как случайные величины T 1 , т ₂,..., T n и заранее точно определены быть не могут, в качестве входных временных параметров взяты числовые характеристики этих величин, представленные их начальными моментами а 1 ( г ) , а ₂ ( т ) .. а^ ( г ) . При этом определяющим для дальнейших вычислений момента времени начала выполнения очередного задания является наиболее поздний момент завершения заданий-предшественников fmax .

Стохастическая модель энергоэффективного управления вычислительной нагрузкой ...

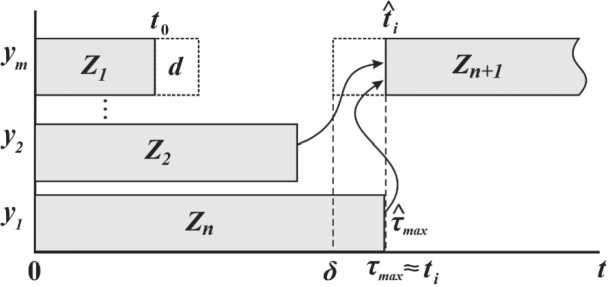
Рисунок 1. Временная диаграмма стохастического вычислительного процесса в МПВС

Источник: [2].

Таким образом, исходными данными для решения задачи энергоэффективного управления стохастическими вычислительными процессами в МПВС являются:

• •    план (расписание) вычислительного процесса, определяющий последовательность выполнения заданий на каждом вычислительном модуле вычислительной системы, пред-

• ставляемую в МПВС в форме матрицы смежности заданий H N,M;

• •    модель однородной вычислительной системы Y = { у 1 , у 2 ,..., y m } - множество процессоров, входящих в вычислительную систему заданной архитектуры. Каждый y _i характери-

• зуется множеством энергосберегающих состояний C^ = {C1,C2 ,...,Cg};

• •    время d , затрачиваемое на решение задачи перевода в энергосберегающее состояние;

• •    начальные моменты f1, т ₂ .„ А n распределения времени т окончания выполнения заданий:

«1 = {«1 (А ),«1 (^2 )-«1 (^п ) «2 = {«2 (А1 ),«2 (Ч )-..а2 (Ап )

« q = ^{{ a} q (А ) , « q (Ч )-^а_Ч (^ п ) , где q = 1, 2, …

В результате решения поставленной задачи должно быть определено следующее:

• •    энергосберегающее состояние C ^* каждого процессора из заданного множества, обеспечивающее минимальное энергопотребление при его вынужденном простое;

• •    момент времени δ начала перевода процессора в активное состояние при завершении выполнения очередного задания-предшественника.

В основе концептуального подхода к решению задачи энергоэффективного управления стохастическими вычислительными процессами в МПВС лежит расчет параметров функции распределения времени завершения задач и использование метода моментов для определения времени начала очередной вычислительной задачи. Рассмотрим этот аспект более подробно.

Через начальные моменты времени завершения задач-предшественников Z1, Z2, …, Zn рассчитываются параметры функции распределения Fj(t) времени завершения каждой такой задачи. Для этого использована аппроксимация неизвестного закона распределения случайной величины f j по заданным начальным моментам и„ (гj) ее распределения к закону распределения Вейбулла – Гнеденко (Вейбулла):

F j ( t ) = 1 - e ^{- (t/ л )} ,

где λ и k – параметры распределения [5].

Задача аппроксимации в данном случае сводится к определению значений параметров λ и k . Решить эту задачу можно, применив подход, представленный в [5].

Используя полученные значения, можно определить параметры распределения максимума времени выполнения нескольких заданий, а через них – функцию распределения F _imax( t ) времени ^r_max. Так как ^г_тах является максимальным временем завершения выполнения всех задач-предшественников, то можно считать, что этот момент времени совпадает с моментом времени t ^ˆ _i – началом выполнения очередного задания. Следовательно, функция распределения F i ( t ) является также функцией распределения и времени t i .

Далее можно определить значение ti. Следует заметить, что значение момента времени ti начала выполнения очередного задания совпадает со случайной величиной fmax - максимальным временем завершения задач-предшественников. Так как моменты времени f1, f2,.„ г N являются случайными величинами и характеризуются соответствующими функциями распределения, то можно найти параметры распределения случайной величины ti:

ti = max { t _v т 2, , t_n } .

Если известны функции Fj(t) (j = 1, 2, …N) распределения времени выполнения каж- дого j-го задания, а через F max(t) обозначена функция распределения случайной величины ti (1), то тогда справедливо

N

F mJ t ) = П F ( ' ) .

j = 1

Начальные моменты a q (f) этого распределения можно найти из соотношения '

to              ” f N ^ N ^       N aq (t) = JtqdFmax (t)dt = Jtq ПFj (t) 91 = EJtqfj (t)ПF (t)dt,

0                      0 ^ j = 1         J         ^j = 1 0             i = 1

j * i

9Fj(t)

где f j ( t ) =----- - плотность распределения вероятностей случайной величины f j .

Для нахождения оценки fmax времени выполнения параллельных процессов необходима аппроксимация каждого неизвестного закона распределения случайной величины f j , заданного начальными моментами a q ( f j ) , к некоторому теоретическому закону F j ( t ) . В качестве F j ( t ) целесообразно выбирать такой закон распределения, который определен на положительной полуоси ( t >  0 ), аналитически дифференцируется и интегрируется и имеет вид, близкий к реальному распределению ^t _j .

На основе расчетов времени выполнения параллельных заданий и момента начала выполнения каждого очередного задания можно определить параметры перевода процессоров в одно из энергосберегающих состояний.

Стохастическая модель энергоэффективного управления вычислительной нагрузкой ...

В общем случае стохастическая модель энергоэффективного управления вычислительной нагрузкой в МПВС представляет собой взаимодействие алгоритмов.

• 1.    На первом этапе выполняется алгоритм определения параметров распределения законов распределения F j ( t ), j = 1,™, N , времени т_у,т_г,...т N завершения выполнения каждого задания, являющегося предшественником очередного задания, по начальным моментам a q ( т j ) . Расчет параметров реализован с использованием метода моментов [5; 6].

• 2.    На втором этапе при использовании результатов аппроксимации F ₁( t ),…, F _N( t ) к некоторому теоретическому закону распределения выполняется алгоритм определения параметров распределения F _max( t ) (3) максимума времени выполнения нескольких заданий-предшественников очередного задания. Аппроксимация F _max( t ) основана на использовании метода квантилей порядка 0,24 и 0,93 [5].

• 3.    На завершающем этапе реализуется алгоритм определения момента времени t _i начала выполнения очередного задания и проверки условия целесообразности перевода процессора в энергосберегающее состояние в период простоя. Момент времени t _i определяется как t i = F m1x ( Р ) , где Р — вероятность того, что время начала выполнения очередного задания не превысит t _i. Проверка условия целесообразности перевода процессора в одно из C -состояний основана на сопоставлении времени простоя и длительности переходных процессов между активным режимом и С -состояниями. При положительном решении по критерию минимальности потребляемой мощности определяется оптимальное энергосберегающее С* -состояние, а также время δ начала перевода процессора в активный режим работы ( С ₀-состяние).

Общее содержание описанной модели представлено на Рисунке 2.

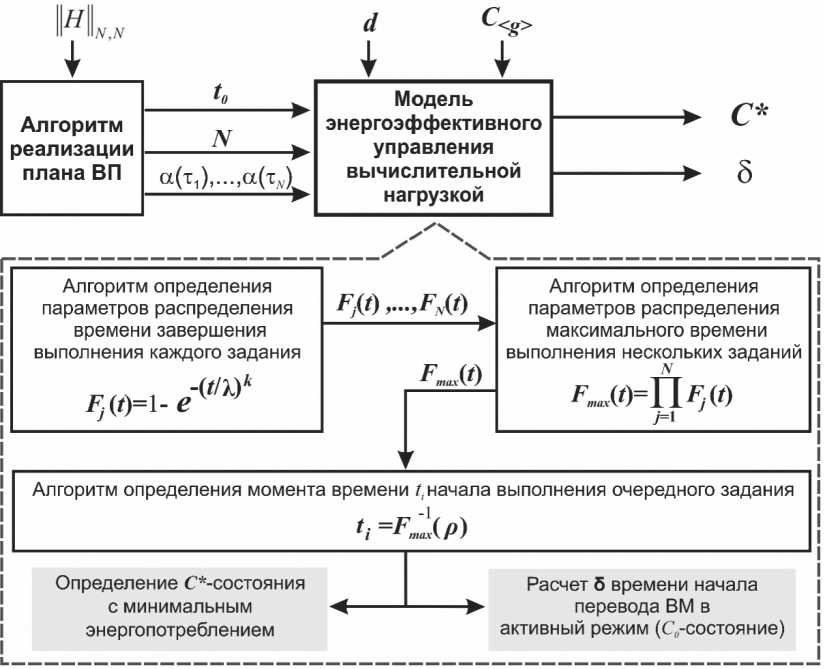
Рисунок 2. Стохастическая модель энергоэффективного управления вычислениями в многопроцессорных системах Источник: составлено авторами.

Следует заметить, что энергоэффективность МПВС в данном случае зависит:

• •    от длительности пребывания каждого процессора в состоянии простоя;

• •    электрической мощности, потребляемой процессором за период вынужденного простоя в процессе вычислений;

• •    количества простоев, которое, в свою очередь, зависит от степени связности задач в составе выполняемого алгоритма.

Заключение

Проведенные исследования показали следующее.

• 1.    Данная модель позволяет снизить энергоемкость параллельных вычислений за счет использования энергосберегающих состояний процессоров в периоды их вынужденных простоев различной длительности. В отличие от метода, изложенного в [1], модель учитывает стохастический характер вычислительных процессов в МПВС.

• 2.    Предлагаемая модель реализует подход к вычислению времени параллельного решения независимых заданий на основе метода моментов и аппроксимации к закону распределения Вейбулла, имеющий относительно невысокую трудоемкость и в то же время точность, достаточную для решения ряда прикладных задач, в том числе задачи оценивания энергоемкости функционирования МПВС.

• 3.    Алгоритмы, составляющие рассмотренную модель, позволяют оперативно определять значения основных временных параметров энергосберегающих состояний и поэтому могут использоваться как при централизованном, так и при децентрализованном управлении вычислительной нагрузкой в МПВС.