Стохастическая модель микроструктурного разрушения на основе восстановления законов распределений случайных полей в микронеоднородных средах

PNRPU MECHANICS BULLETIN

Состояние и эволюция внутренней структуры твердых тел играет ключевую роль с точки зрения их физико-механических характеристик. Для изучения закономерностей изменения внутренней структуры часто применяются различные дискретные модели материалов, к числу наиболее распространенных из которых относится метод молекулярной динамики (МД). В частности, в настоящее время метод молекулярной динамки широко применяется для изучения [63]:

• •    полимеров: цепочек, колец и разветвленных молекул, процессов релаксации и явлений переноса;

• •    биомолекул: структуры и динамики белков, стыковки молекул, мембран, мицеллы, сворачивания белков;

• •    динамики жидкости: ламинарного потока, пограничных слоев, реологии неньютоновских жидкостей, неустойчивых потоков;

• •    твердых тел, в том числе кристаллов: образования и миграции дефектов, разрушения, границ зерен, структурных превращений, влияния радиации, упругих и пластических свойств, трения, изучения поверхностных слоев, получения покрытий методом послойной осадки из газовой среды.

Кратко напомним основную идею и соотношения МД. Основная идея метода молекулярной (атомарной) динамики заключается в представлении тела в виде дискретных взаимодействующих частиц (атомов) и (численном) решении классических уравнений движения Ньютона, описывающих это взаимодействие. При этом уравнение движения частицы с радиусом-вектором r _i имеет следующий вид (см., например, [8] или [3]):

NN mri= E Ф(rj)+ E T(ry,rj)+v(ri,ri), j=1, j * i j=1,j * i (1)

Ф к)=-v U(rj), где rj - радиус-вектор, соединяющий частицы с номерами i и j, rj = ri - rj; Ф (r) - консервативная составляющая взаимодействия частиц, описывающая силы взаимодействия, как правило, имеющие электромагнитный характер; U (r) - потенциал межатомного взаимодействия; Y(r, r) описывает неконсервативную (диссипативную) составляющую взаимодействия частиц и часто вводится как некоторая фиктивная сила для описания «внутреннего трения», а v (r, r) - внешние силовые поля (которые иногда также разделяют на консервативную и неконсервативную составляющие). Так, например, для описания процесса осаждения частиц атомных размеров из газовой атмосферы часто необходимо учитывать силу тяжести, а для описания трения в области зоны контакта поверхностей – вводить «силу трения». Далее систему уравнений (1) необходимо снабдить совокупностью начальных (и в общем случае – граничных) условий и решить численно с применением той или иной схемы интегрирования.

Очевидно, что ключевым вопросом метода является выбор потенциала межатомного взаимодействия U ( r ) , поскольку именно потенциал полностью описывает реальное физическое взаимодействие частиц друг с другом (в отличие от двух других слагаемых правой части (1), которые используются для учета внешнего воздействия или для описания объемной диссипации). В настоящее время существует множество потенциалов межатомного взаимодействия, которые описывают те или иные свойства исследуемых материалов, необходимые при исследовании различных процессов (например, упругие характеристики кристаллической решетки, коэффициенты теплового расширения, свойства точечных и линейных дефектов, свойства фазовых переходов, в том числе твердотельных, и многие другие).

Исторически сложилось, что идея и методологические вопросы метода молекулярной динамики: корректное определение граничных и начальных условий, решение вопросов о представительности расчетной области, применение устойчивых численных схем интегрирования уравнений движения и связанный с этим вопрос о выборе шага интегрирования, вопросы поддержания микроканонических ансамблей, например, изотермоизобарических (NPT) или изотермо-изохорических (NVT) и других, – развивались с некоторым запозданием по сравнению с исследованиями, в которых рассматривались частные по отношению к МД вопросы описания характера взаимодействия атомов в различных системах (или, что то же самое, предлагались различные потенциалы межатомного взаимодействия). Так, если ключевыми работами, заложившими основы методов МД, являлись работы, опубликованные в середине XX века (а частности, статьи B.J. Alder и T.E. Waingwright [7] и J.B. Gibson, A. N. Goland, M.Milgram и G.H. Vineyard [41]), то частные вопросы описания взаимодействия частиц поднимались еще за 20–30 лет до этого.

Например, один из наиболее «популярных» среди исследователей потенциал Леннард– Джонса был предложен последним еще в 1924 г. [47] для описания парного взаимодействия сферических неполярных молекул, потенциалы типа Морзе, первоначально предложенные как приближение для энергии двухатомной молекулы – в конце 20-х гг. XX в. [60], а потенциал Штокмайера для взаимодействия молекул, обладающих постоянным дипольным моментом – в 1941 г. [68]. В последние же десятилетия ситуация существенным образом меняется: при уже достаточно «устойчивой» теоретической и вычислительной основе методов МД вновь встают вопросы, связанные с построением и идентификацией потенциалов межатомного взаимодействия. Уже давно известно, что использование классических парных потенциалов (Леннард–Джонса, Морзе, Ми и др.) дает не вполне корректные результаты при моделировании металлов и некоторых других материалов по причине учета лишь электромагнитных сил парного взаимодействия: такие потенциалы не позволяют получить устойчивую конфигурацию для кристаллических решеток, не относящихся к плотноупакованным; например, ОЦК или простая гексагональная решетки оказываются неустойчивыми при использовании большинства парных потенциалов. Начиная с 80-х гг. XX в. развиваются подходы к моделированию структуры и свойств металлов и сплавов с использованием потенциалов, основанных на так называемом методе погруженного атома (ЕАМ), в котором в отличие от парного потенциала учитываются не только взаимодействия между атомами, а еще и взаимодействия электронных облаков с атомами и, наоборот, атомов с облаками. Следует отметить, что такой подход к описанию энергии атомной системы оказался чрезвычайно удачным при моделировании внутренней структуры и физико-механических свойств металлов и полупроводников (в широком смысле – всех кристаллических твердых тел, а в некоторых случаях – и жидких и/или аморфных сред), что подтверждается огромным количеством исследований и публикаций по этому направлению. Цель настоящего обзора (не претендующего на всеобъемлющий охват всех существующих подходов к построению и анализу потенциалов, построенных на методологии EAM) в том, чтобы дать читателю общее представление о текущем состоянии и тенденциях развития современной (последних 10–15 лет) молекулярной динамики в части разработки и верификации EAM-потенциалов для различных материалов. Авторы обзора постарались, с одной стороны, обратить внимание на «классические» подходы к построению современных EAM-потенциалов, а также выделить некоторые специфические работы, связанные с построением потенциалов и исследованиями свойств материалов, имеющих важное значение для современной техники (материалы для атомной энергетики, аэрокосмической промышленности, биомедицины и т.д.). Обзор состоит из двух логически связанных частей: вначале внимание обращено к работам, в которых разработаны методологические основы метода, в том числе решение важного вопроса о подходах к идентификации параметров потенциала, и в которых рассматриваются однокомпонентные атомные системы и материалы; вторая часть обзора посвящена современному состоянию МД в части описания структуры, свойств и поведения многокомпонентных (бинарных и тернарных) систем.

При этом важно понимать, что метод молекулярной динамики имеет свои, часто довольно существенные, ограничения. В силу того, что движение частиц описывается лишь с помощью второго закона Ньютона, МД неприменим для описания материалов, в которых квантовые эффекты играют основную роль во взаимодействии между частицами (что характерно для процессов, происходящих при экстремально высоких температурах, на сверхмалых расстояниях между атомами или при чрезвычайно малых характер- ных временах процессов) [61, 72]. Второе существенное ограничение МД связано с невозможностью моделировать реальные технологические процессы из-за огромной вычислительной сложности метода, так как сегодняшний уровень развития вычислительной техники позволяет рассматривать системы размером до кубического микрометра [2].Таким образом, в настоящее время с применением МД невозможно решать реальные технологические задачи, поскольку применимость метода даже с учетом возможностей суперкомпьютерной техники и технологий высокопроизводительных вычислений в настоящее время ограничена системами не более чем из 109–1010 частиц.

• 1.    Обзор потенциалов для однокомпонентных систем

  Первые работы, предвосхитившие появление модели погруженного атома ( ЕАМ – embedded atom method ), относятся к 1983 году и связаны с именами M.S. Daw и M.I. Baskes [30]. Основными предпосылками появления модели ЕАМ являлись различные теоретические работы в области фундаментальных исследований, направленных на изучение энергии и структуры примесей, поверхностей раздела (так называемых «интерфейсов») и других дефектов в кристаллических структурах многих материалов. Зачастую такие теории имели существенные практические ограничения из-за принятых при их построении «сильных» предположений. Так, например, методы теории групп [40, 66] и кластерные методы [56], как правило, ограничены размерами и требованием периодичности рассматриваемых множеств. Как в теоретико-групповом, так и в кластерном подходах полная энергия системы представляет собой сумму многих одноэлектронных энергий. Альтернативой таким моделям выступали парные потенциалы межатомного взаимодействия, построение («конструирование») которых проводилось из фундаментальных или эмпирических соображений. Однако использование парных потенциалов оказалось успешным лишь для относительно небольшого ряда задач, связанных в первую очередь с описанием инертных и химически неактивных элементов (например, He). Применение парных потенциалов для описания металлов с ОЦК или гексагональной структурой показало себя не вполне корректным: так, при термостатировании происходит самопроизвольное перестроение таких решеток в ГЦК-структуру. Кроме того, часто используемые в МД для описания однородного деформирования образца периодические граничные условия (ГУ) затрудняют моделирование процессов теплового расширения и накладывают ограничения на размеры области моделирования по сравнению с характерными масштабами дефектов, расположенных в этой области.

Основываясь на идеях квантово-механической теории функционала плотности ( DFT – density functional theory ), а точнее, теории квазиатома [69] и модели эффективной среды [62], M.S. Daw и M.I. Baskes в работе [29], опубликованной в 1984 г., предложили разделять полную потенциальную энергию системы взаимодействующих атомов на энергию парного взаимодействия и так называемую энергию «погружения». Предполагается, что каждый атом локально окружен электронным газом и, таким образом, испытывает влияние от соседних электронных облаков. Расчет электронных плотностей осуществляется согласно теории Хартри-Фока [5] (более подробные описания расчетов даны в работах [25, 53]). Энергия погружения определяется как избыточная энергия, которой обладает атом в электронном газе однородной плотности по сравнению с потенциальной энергией взаимодействия атома, отделенного от этого электронного газа. Полная энергия системы, вычисленная с помощью ЕАМ-потенциала, имеет вид

E toal = L E i , i

^Ei = F i ( p i ) + 1 Е ф j ( j ,

• ² j , j * i

pi=E ф( j, где Ei – потенциальная энергия отдельного атома во взаимодействии с окружающей его средой; Fi - функция погружения; pi - электронная плотность вблизи атома i; ф - вклад плотности заряда электронов от j-го атома в месте расположения i-го атома; ф^ - энергия парного взаимодействия атомов i и j (включая их электронные оболочки, но без учета «потерянных» электронов внешних орбиталей, но не учитывая электронный газ); rij– расстояние между атомами i и j. Приведем описание имплементации подхода ЕАМ к уравнениям движения атома (1), используемых в молекулярной динамике [3]. Первое слагаемое в правой части (1) является важнейшим фактором движения частиц и в случае использования EAM-подхода определяется следующим образом:

ф ( r ¹ г Е,,.,

-V, £ Е  Г

i

F ⁽p i ^{) +} E ^УЕфЛ j j* i                  j * i

=-E j * i

dFi (p) Sp

P=P i

I 5Fi (P) Sp

P=P. j 7

d у j ( r ) dr

₊ d ф j ^{( r} ) dr

^- r

r ij

где r ij – расстояние между атомами i и j .

Результаты, полученные при использовании такого подхода к построению потенциала, позволили с высокой точностью описать широкий ряд физико-механических свойств (например, упругие постоянные, свойства точечных, поверхностных дефектов, диффузионные свойства и др.) исследуемых материалов, что, в свою очередь, вызвало большой интерес со стороны исследователей и способствовало формированию нового направления в молекулярной динамике. Стоит отметить, что в литературе часто при использовании потенциала ЕАМ говорят о так называемом потенциале Finnis–Sinclair (FS) [36], который является частным случаем семейства потенциалов, построенных с применением методологии ЕАМ. Потенциалы типа FS впервые дали «хорошее» согласование с экспериментальными данными для материалов с ОЦК кристаллической структурой (например, Fe, V, Nb, Ta, Mo, W) и в каком-то смысле явились предтечей EAM-подхода.

Несмотря на то, что первые ЕАМ-потенциалы [37, 38] удовлетворительно описывали целый ряд свойств различных материалов (что не удавалось сделать с помощью парных потенциалов межатомного взаимодействия), было обнаружено, что они достаточно хорошо описывают лишь свойства материалов с ГЦК-структурой [10]. Упругие константы, полученные в ходе расчетов с использованием потенциалов ЕАМ для материалов с направленными связями (например, для кремния Si), плохо согласовывались с экспериментальными значениями, что связано с тем, что формулировка модели ЕАМ предполагает сферическое усреднение плотности электронных облаков, вследствие чего теряется учет направленности связей. Поэтому практически сразу после опубликования пионерской ра- боты в 1984 г. M.I. Baskes и др. продолжили попытки создания и внедрения более точной и универсальной модели, способной описать многие свойства исследуемых материалов, и уже в 1987 г. опубликовали работу [10]. Авторы предложили так называемую модифицированную модель погруженного атома (МЕАМ), которая основывалась на ранее разработанном ЕАМ-подходе. Основной новизной предложенной модели являлось включение различия между ковалентными и металлическими связями за счет явного учета угловых взаимодействий в функции электронной плотности. Функция погружения в рамках формализма MEAM имеет вид

F ( p ) = AE c Л‘" p

p

p

где А - материальный параметр; E c - энергия связи; p - электронная плотность структуры с минимальной потенциальной энергий (то есть атомной конфигурации, в которой атомы находятся в положениях устойчивого равновесия); p - суммарная электронная плотность, включающая парциальные вклады сферически-симметричной электронной плотности p ⁽⁰⁾ и плотности p ⁽¹⁾, p ⁽²⁾, p ⁽³⁾, учитывающие угловые вклады 5 -, p -, d -, f -орбиталей соседних атомов [44]. Частичные электронные плотности объединяются с помощью вспомогательной функции

p^{( k} ) p⁽⁰⁾

г = 2 1 ⁽ k ) k = 1

где t(k) – материальные параметры, описывающие «несимметрию» (анизотропии) оболочек по трем направлениям. Полная электронная плотность вокруг частицы в таком случае принимает вид p,=p’0) G (Г), где функция G (Г,.) выбирается исходя из особенностей исследуемого материала. Стоит отметить, что в формализме МЕАМ конкретная форма функции парного взаимодействия ф( r) не задается, а значение функции парного взаимодействия получается как разность полной энергии и функции погружения (эта функция в «контрольном» соотношении будет зависеть только от расстояния, так как электронные плотности при расчете являются функциями от расстояния). Полная энергия, вычисленная в расчете на один атом, получается из уравнения, предложенного J.H. Rose и др. [64],

E “ ( r ) = - E_c ( 1 + a * ) exp [- a * ] ,

*                9 B Q^ ¹/²

a =( r / ro —1) —— , V Ec J где Ec – энергия атомной связи; r0 – расстояние до первого соседа в эталонной структуре (радиус первой координационной сферы); B – (изотропный) объемный модуль упругости; Q - равновесный объем элементарной ячейки. Таким образом, парный потенциал имеет вид

Ф»(Гц ) = "11 2 E-

1 ij \ ij J 7 i

u

ij

(r )F (p/( Гу))-F (py( Г-))

где Z_ij – число ближайших соседей атомов i и j .

Кроме учета угловых взаимодействий, при построении потенциала МЕАМ важным остается вопрос о так называемом радиусе обрезания r cutoff (если расстояние между двумя атомами превышает r cutoff , то считается, что взаимодействием между парой атомов можно пренебречь). Традиционно при использовании модели типа ЕАМ диапазон взаимодействия ограничивается за счет плавного усечения функций вблизи точки отсечения при помощи различного рода экспоненциальных или гиперболических зависимостей. Обоснованием такой процедуры является то, что силами взаимодействия, возникающими между атомами на больших расстояниях, можно пренебречь. Однако такой способ не является универсальным, так как на практике чаще всего спад на больших расстояниях не происходит достаточно быстро, поэтому потенциал взаимодействия необходимо искусственно продолжать. C.L. Fu и др. [39] показали, что при описании релаксации атомной системы важны только взаимодействия с атомами, попадающими в первую координационную сферу. Это относится и к материалам с ОЦК-структурой, несмотря на то, что отношение расстояний между второй и первой координационными сферами составляет лишь 1,15. В работе [12] предложена схема, накладывающая дополнительные ограничения на функции взаимодействия. Обоснование такой схемы состоит в том, что атом, находясь между другими атомами, способен «экранировать» взаимодействие между этими «внешними» атомами. Таким образом, расчет взаимодействия происходит только между ближайшими соседями, а взаимодействия с более «отдаленными» атомами происходит путем переноса ближайших взаимодействий, отмасштабированных с помощью так называемого скринингового фактора, имеющего вид [59]

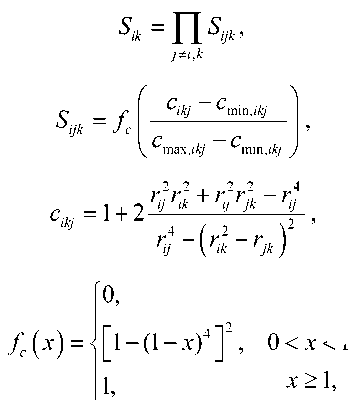
S_ik = П Sy к ik ijk

J' * i , k

’,                     x <  0,

1 - (1 - x)4 ]\  0 < x < 1, x > 1,

/_c ^{( x} )

где i – номер рассматриваемого атома; j – один из ближайших соседей атома i ; k – экранируемый атом; c ikj – скрининговые параметры; r ij – расстояния от атома i до атома j . Учет скринингового фактора происходит путем его умножения на функцию парного взаимодействия, а также функцию электронной плотности.

В рамках рассмотрения подхода МЕАМ к построению потенциалов межатомного взаимодействия стоит отметить работу Z. Bangwei и др. [9], в которой предложен более простой аналитический МЕАМ-потенциал, являющийся модификацией потенциала, предложенного

M.I. Baskes [10]. В [10] электронная плотность каждого атома определяется сферическим усреднением и аппроксимируется суммой плотностей соседних атомов. Однако в действительности распределение электронов внешней оболочки отклоняется от сферической симметрии, следовательно, линейная аппроксимация электронной плотности является не вполне корректной. Предложенная в работе [9] модификация потенциала отличается от [10] тем, что электронная плотность рассматривается способом, аналогичным ЕАМ, однако к общему выражению энергии добавляется энергетический член M ( P ), который используется для выражения разности между фактической полной энергией системы атомов и рассчитанной из исходной ЕАМ-модели с использованием суперпозиции сферических электронных плотностей. При таком подходе полная энергия системы выражается следующим образом:

Eoal = £ F (p,) +1 ZS»j (rj ) + Z Mi( P), i 2 i j, j * i i pi=1L*( rj),

p=]l ф2 (rj).

Функция M ( P ) не имеет универсальной формы, то есть для аппроксимации экспериментальных данных подбирается эмпирически. Результаты, полученные с использованием предложенной модели, хорошо согласуются с входными экспериментальными данными: постоянной решетки, энергией связи, модулем сдвига, коэффициентом анизотропии, а также позволяют достаточно точно определять энергию вакансии. Кроме того, упругие константы, рассчитанные с помощью модели для различных ОЦК-материалов, в точности совпадают с экспериментальными значениями.

Несмотря на стремление большинства авторов при построении ЕАМ-потенциалов описать максимальное количество физико-механических и геометрических свойств, которые не участвуют в верификации параметров, как правило, сделать это удается лишь для некоторой вполне определенной заранее группы свойств (например, для упругих свойств, характеристик фазового перехода, диффузионных свойств и др.). Достигается это путем создания набора «эталонных» параметров, полученных в ходе экспериментов или же в квантово-механических расчетах [5]. Следует отметить, что второй подход в литературе часто называют основанным на «первых принципах» ( ab initio ), однако использование этого термина представляется не вполне корректным, поскольку в любом случае при решении соответствующих уравнений исследователи вводят те или иные предположения о характере решения, поэтому далее при упоминании такого подхода более уместным представляется использование термина «квантово-механических расчеты». Чаще всего таким набором параметров выступают: парные корреляционные функции ( PCF – pair correlation function ) [22]; структурный фактор ( TSF – total structure factor ) [33] – характеристика рассеивания рентгеновского излучения; свойства переноса; характеристики фазового перехода; параметры решетки; силовые характеристики (полученные, как правило, с использованием квантово-механических расчетов) и др. В зависимости от выбранного набора параметров для верификации параметров потенциала исследователь получает возможность построить потенциал таким образом, чтобы при моделировании с помощью полученного потенциала (например, в расчетах молекулярной динамики) быть уверенным в точном воспроизведении нужных ему свойств.

В качестве примера использования такого подхода приведем работы, посвященные построению потенциалов для бериллия Be. Основная особенность Be заключается в особенностях его строения: межатомные связи являются направленными, поэтому работы, посвященные построению межатомных потенциалов для Be, как правило, использовали потенциалы МЕАМ для включения эффекта угловых сил: например, в работе [13] авторы предложили МЕАМ-потенциал, который позволял рассчитать параметры решетки и энергии связи, хорошо согласующиеся с экспериментальными данными, однако при этом потенциал оказался непригодным для учета зависимости этих свойств от температуры, из чего был сделан вывод, что только лишь описания направленности связей недостаточно для корректного описания термодинамических свойств. В работе [6] предложен ЕАМ-потенциал для Be, имеющего гексагональную структуру кристаллической решетки. Следует отметить, что предложенный потенциал является самым точным ЕАМ-потенциа-лом для Be на настоящий момент, хотя в явном виде и не учитывает направления атомных связей. В качестве функции парного взаимодействия выбран потенциал, основанный на парном потенциале Морзе и имеющий вид [60]

ФMorse (Г) = Dc (e-2а('-rc)- 2e-а(’-■)), где Dc - энергия связи; rc - длина равновесной связи; а - вторая производная функции потенциальной энергии в точке минимума. Результирующий парный потенциал имеет следующий вид:

Ф res ( r ) = Ф Morse ( r ) ^- ф ( r cutoff ) +

r cutoff m

m

Г

V ' cutoff 7

d ф dr

r cutoff

где r cutoff – радиус обрезания потенциала; m – материальная константа. Такая форма парного потенциала обеспечивает непрерывность функции парного взаимодействия и ее производных при различных значениях радиуса обрезания r cutoff . Функция электронной плотности выбрана в классическом экспоненциальном виде [46]:

f (r ) = Ae - B (r - rc), где A, B – параметры потенциала, а в качестве функции погружения использовалась функция Джонсона [45]

F (p) = Fo

<   лв

1 - ln -p vpo 7

где F _o и F 1 - константы; p ₀, в , у - параметры потенциала.

Качество подгонки контролировалось с помощью взвешенной суммы квадратов разностей:

N ₂

G = V w I f / n - f (h J , i I i (calc)         i (obs) I , i=1

где w - веса, определяемые исследователем; f i ( _calc ) и f i ( _obs ) - расчетные и экспериментальные значения наблюдаемых параметров.

Подбор параметров потенциала проводился с помощью метода Ньютона–Рафсона. В качестве экспериментальных данных использовались значения упругих постоянных и энергия связи. Кроме того, в экспериментальные данные были внесены значения энергии образования вакансии, полученной из расчетов с применением моделей квантовой динамики. Полученный потенциал сравнивался с рядом предшествующих ему потенциалов [13, 48] и др. Потенциал правильно предсказывает стабильную конфигурацию кристаллической решетки и может быть использован для моделирования структуры материала, а также повреждения радиоактивным излучением (что является актуальной задачей в связи с частым использованием бериллия для производства радиационных окон рентгеновских трубок). Потенциал хорошо подходит для изучения нелинейного расширения, а также для описания свойств точечных и линейных дефектов, однако предсказываемая температура плавления для потенциала составляет 1200–1300 К, что не согласуется с экспериментальными данными (1560К). В силу того что большинство других потенциалов для Be строились методом MЕАМ, предложенный потенциал имеет преимущество в вычислительной эффективности.

В общем случае параметры ЕАМ-потенциала для конкретного материала идентифицируют один раз, а затем используют для исследования структуры и свойств материала как в твердом, так и в жидком состоянии. Однако такой подход не совсем корректен и вызывает ряд вопросов, связанных в первую очередь с адекватным описанием динамических свойств и свойств переноса, так как в большинстве случаев ЕАМ-потенциалы дают хорошее согласование с экспериментом в сравнительно небольшом диапазоне температур. В работе [27] авторы рассмотрели вопросы переносимости эффективных ЕАМ-потенциалов твердой фазы для изучения свойств жидкой фазы Cu. При построении потенциала использованы вид функции погружения, электронной плотности, а также парного взаимодействия, предложенные в работах Ю. Мишина и др. [58] и M. Doyama и др. [32], после их репараметризации (первоначально параметры этих потенциалов были предложены в работе [28]). Переносные свойства (самодиффузия) предложенных потенциалов сравнивались с помощью схемы, предложенной L.E. Gonzalez и др. [42]. Сравнивая потенциалы, авторы [27] пришли к выводу, что потенциал, предложенный M. Doyama и др., лучше согласуется с экспериментальными данными и его можно использовать для получения представления о понимании микроскопического поведения некоторых металлов и сплавов.

Работы Д.К. Белащенко и др. [15–18] представляют собой серию статей, в которых одним и тем же способом осуществляется построение ЕАМ-потенциалов для жидких (высокотемпературных) Li, Na, Cu, U и др. Для построения потенциала использовались данные, полученные с помощью метода дифракционной микроскопии при температуре, близкой к температуре плавления материалов. Согласно экспериментальным данным оценивались критические параметры материалов (температура, давление, плотность). Структура жидких материалов оценивалась с помощью парных корреляционных функций ( PCF ). Подбор параметров парной части потенциала выполнялся путем построения и идентификации прямой МД-модели по дифракционным данным с использованием алгоритма Шоммерса [65], который был продолжен на область малых расстояний (в случаях высоких давлений) с помощью экспоненциальной формулы Борна-Майера [31]. Подбор параметров осуществлялся с помощью оценки невязки между дифракционной и модельной PCF. Затем построенные потенциалы использовались для моделирования и оценки структуры, диффузионных свойств и температуры плавления исследуемых материалов. Сравнение полученных результатов с экспериментальными данными позволяет утверждать корректность предложенного потенциала.

М.И. Менделев и др. [43, 54] предложили несколько ЕАМ-потенциалов для ОЦК Fe, моделирование которого, как известно, сильно осложнено из-за наличия у него магнитных свойств. Ранее потенциалы для Fe были построены B.-J. Lee и др. [51] методом МЕАМ, однако температура плавления в расчетах получалась равной 2200 К (при эмпирическом значении 1812 К). В [54] на примерах работ предшественников было показано, что использование данных, относящихся к свойствам исключительно идеальных кристаллов, недостаточно для потенциалов типа ЕАМ ввиду их плохого согласования со значением структурного фактора ( TSF ) жидкости. Дополнить процедуру подбора параметров было предложено двумя способами: включением данных о межатомных силах, полученных из квантово-механических расчетов, или экспериментальных данных, полученных с помощью дифракционной микроскопии. Первый способ подразумевает следующее : генерируется атомная модель для жидкости с правильной (заранее известной) плотностью, затем выполняется квантово-механический расчет результирующих сил на всех атомах, и значения сил используются для определения параметров потенциала (вид потенциала выбирается заранее). Такой метод подбора параметров в литературе принято называть методом «согласования сил» ( force-matched method ). Процедура обеспечивает рассмотрение ряда атомных геометрий, включая случаи малых атомных расстояний. МД-модель состояла из 100 атомов, что связано с большими вычислительными затратами квантово-механических расчетов. Второй способ подразумевает использование для подбора параметров потенциала данных парной корреляционной функции ( PCF ), а также параметров ГЦК- и ОЦК-решетки. Преимущество первого подхода заключается в том, что данные дифракции доступны не всегда. Наоборот, преимущество потенциалов, построенных по дифракционным данным, обусловлено тем, что МД-модели лучше согласуются с экспериментальными данными, что связано с тем, что расчеты с использованием моделей квантовой динамики, как правило, выполняются для идеальных кристаллов. Исходя из предложенных в работе данных стоит отметить, что второй способ (то есть по данным дифракционной микроскопии) оказался несколько лучше, так как более точно воспроизводил значения энергии связи, а также параметры парной корреляционной функции. Однако нельзя утверждать, что использование данных, полученных из квантово-механических расчетов, позволяет строить ЕАМ-потенциалы для любых систем без использования дифракционных данных. В качестве примера стоит отметить работу [34], в которой процедура построения потенциала с помощью квантово-механических расчетов для чистого алюминия происходила похожим образом, однако согласие с экспериментальными данными по структурному фактору ( TSF ) было плохое (несмотря на хорошее согласование с температурой при заданном давлении).

В работе H. Chamati и др. [21] предложен ЕАМ-потенциал для Fe, разработка которого была нацелена на исследование свойств самодиффузии. Эффективная парная функция взаимодействия частиц строилась с помощью суммы двух функций взаимодействия Морзе. Функции погружения аппроксимируются полиномами 4-й степени по экспериментальным точкам. Подбор параметров происходил путем минимизации взвешенного квадрата отклонений значений выбранных свойств исследуемого материала от их целевых (экспериментально известных) значений. Экспериментальный набор параметров включал в себя параметры решетки, некоторые значения потенциальной энергии взаимодействия атомов, объемный модуль упругости, упругие константы, энергию связи ослабленной вакансии, энергию миграции точечных дефектов, а также среднюю поверхностную энергию. Полученный потенциал точно описывает свойства кристаллической решетки, тепловое расширение, а также свойства точечных дефектов для ОЦК и высокотемпературной ГЦК-фазы Fe. Построенный потенциал использовался для моделирования самодиффузии одиночных атомов в температурном интервале 600–950 К. Температурные зависимости коэффициентов диффузии, полученные в численных экспериментах, согласуются с законом Аррениуса. Построенный потенциал также позволил обнаружить, что коэффициенты диффузии с диагональным механизмом обмена примерно на порядок выше, чем при механизме «прямого скачка» и механизме «недиагонального обмена».

В работе M.-C. Marinica и др. [52] предложены и сопоставлены 4 варианта потенциала для чистого W. Сначала вводится разделение наборов данных, по которым происходит построение потенциалов:

• 1.    экспериментальные данные, под которыми понимаются экспериментально измеряемые свойства твердого тела: параметры решетки, энергия связи и упругие константы С 11 , С 12 , С 44 (в нотации Фойгта [4]);

• 2.    данные, полученные из квантово-механических моделей (или, точнее, при использовании теории функционала плотности): энергия образования основных точечных дефектов вольфрама (вакансии и междоузельного атома);

• 3.    данные, полученные из квантово-механических моделей: характерное расположение атомов в жидких (случайных) состояниях.

Форма ЕАМ-потенциала соответствовала предложенной в работе М.И. Менделева [54]. Процедура подбора параметров заключалась в вычислении всех параметров трех функций (парной функции, функции электронной плотности и функции погружения) и основывалась на принципе вариационной ассимиляции [50]. Целевая функция, используемая для минимизации отклонения, выглядела следующим образом:

J(A) = Z[Yb. - Yobs (A)] +Xw [Fb-». -F (A)]2, obs где А - вектор набора параметров потенциала; Yobs и Yobs (A) - значения набора параметров, полученных экспериментально, и значения, вычисленные с использованием набора параметров А , F*ab intiio и Fi (A) - силы, действующие на атом i, вычисленные с помощью квантово-механических расчетов и с помощью полученного потенциала ЕАМ; wobs и wi – подгоночные параметры. Варьирование параметрами wobs и wi в работе позволило получить четыре ЕАМ-потенциала одного типа, отличающихся значениями параметров. Все эти потенциалы хорошо описывают образование и характеристики винтовых дисклокаций вольфрама, а также возникновение радиационных дефектов, что не удавалось сделать в более ранних исследованиях. Данные, полученные с использованием первого потенциала, не согласовывались с некоторыми данными, полученными с использованием теории функционала плотности (DFT), поэтому в дальнейшем первый потенциал был исключен из использования.

В работе [24] проведено сравнение четырех потенциалов МЕАМ, предложенных Baskes [11], с двумя потенциалами ЕАМ, предложенными J.E. Angelo и др. [14] и J. Cai и др. [20], построенных для жидкого Ni, причем вид функций и методы подбора параметров потенциалов были различны. Подбор параметров потенциала J.E. Angelo происходил по экспериментальным данным, которые включали в себя упругие модули, параметр решетки, энергию образования вакансии, энергию дефекта упаковки и энергию устойчивости ГЦК-фазы к фазам ОЦК Ni, с помощью нелинейного метода наименьших квадратов, разработанного в Sandia National Laboratories. Построение потенциала J. Cai и др. проводилось по такому же набору экспериментальных данных, как и в случае с первым потенциалом, одна- ко процедура подбора параметров осуществлялась путем минимизации отклонения экспериментальных и модельных данных с помощью симплекс-метода. Потенциалы, предложенные в работе [11], были построены по схеме, описанной в работе [12]. Для этих шести потенциалов (четыре потенциала M.I. Baskes и два потенциала J.E. Angelo и J. Cai) выполнялось МД-моделирование структуры и свойств Ni при низких давлениях и температурах, превышающих температуру плавления, в котором оценивались свойства переноса (коэффициенты диффузии, вязкость и др.), структурного фактора (TSF), значение температуры плавления. В результате было показано, что потенциал, предложенный J.E. Angelo и др., дает худшее согласование по температуре плавления, в то время как другие потенциалы описывали это значение достаточно точно; с другой стороны, потенциал J.E. Angelo и др. хорошо согласуется по экспериментальным значениям энергии связи. Проведенные численные эксперименты с использованием вышеперечисленных потенциалов позволяет судить о том, что коэффициент самодиффузии и вязкость зависят от особенностей структуры жидкой фазы в пределах радиусов второй-третьей координационных сфер.

В работе M.R.Fellinger и др. [35] предложен ЕАМ-потенциал для Nb. Актуальность исследования материала заключается в его свойствах: низкая плотность, высокая температура плавления, биосовместимость делают его привлекательным материалом для использования в сплавах различного рода (например, в медицине создаются прочные и нетоксичные соединения Ti–Nb). Парная функция, функции погружения и электронной плотности были построены в виде кубического сплайна. В работе использовался метод «согласования сил»: полученные в ходе квантово-механических расчетов значения межатомных сил и энергии, вычисленной на один атом, вносились в базу данных и использовались при подборе параметров ЕАМ-потенциала с помощью корректировки относительно отклонения параметров, полученных с помощью потенциала в квантово-механических расчетах и ЕАМ-потенциала [19]. Расширение наборов значений физических величин, полученных из квантовомеханических расчетов, путем добавления значений этих же величин при различных температурных состояниях позволяет использовать потенциал для широкого диапазона температур. В целом подбор параметров ЕАМ-потенциалов с использованием метода «согласования сил» является задачей оптимизации в многомерном пространстве. Функции ЕАМ-потенциала параметризуются с помощью кубических сплайнов, а программа POT-FIT [19] оптимизирует сетку сплайн-узлов, используя комбинации имитируемых алгоритмов отжига [71] и сопряженных градиентов [1]. Стоит отметить, что полученный потенциал успешно прошел верификацию на свойствах, не включенных в набор данных для идентификации параметров: потенциал точно описывает структурные и упругие свойства, свойства точеных и линейных дефектов, однако не очень хорошо подходит для исследования ударной волны и радиационного воздействия. Кроме того, в цитируемой работе подчеркивается, что на основе построенного потенциала имеется возможность строить потенциалы и для сплавов ниобия с помощью метода ЕАМ.

В работе [55] предложены три ЕАМ-потенциала для чистого Ti, представляющего большой интерес в аэрокосмической и медицинской отрасли благодаря высокой прочности, низкой плотности и коррозийной стойкости. Несмотря на это, в литературе относительно мало работ, посвященных изучению внутренней структуры Ti, что связано с малым количеством информации (например, о критических значениях различных параметров), а также особенностями структуры, которые обусловлены наличием двух устойчивых фаз Ti : ГПУ (α-фаза) и ОЦК (β-фаза). Исходные данные, по которым происходило построение и идентификация параметров потенциала, разделены на четыре группы:

• 1.    базовые свойства кристалла (параметр решетки, энергия связи, упругие константы при 0 К);

• 2.    энергия образования точечных дефектов;

• 3.    энергия образования плоских (планарных) дефектов;

• 4.    параметры фазового перехода.

Использование данных первой группы при подборе параметров гарантирует, что ГПУ-структура является более стабильной фазой и позволяет подобрать правильный энергетический «масштаб». Значения параметров второй группы позволяют воспроизводить свойства самодиффузии. Данные об энергии упаковки, относящиеся к третьей группе, обеспечивают корректные результаты при моделировании пластической деформации. Четвертая группа содержала информацию о температуре плавления β-фазы, температуре фазового перехода α–β и скрытые теплоты этих переходов. Стоит отметить, что построенные потенциалы были изначально предназначены для описания как жидкой, так и твердой фазы Ti. Для всех трех потенциалов вид и значения параметров функции электронной плотности совпадали, функции погружения и парного взаимодействия имели один и тот же вид в каждом из трех потенциалов, но значения подгоночных параметров были разными, что обусловлено выбором различных весовых коэффициентов при подгонке потенциала к экспериментальным данным. Основная задача при построении первого потенциала заключалась в воспроизведении данных четвертой группы, однако полученный потенциал плохо согласовывался с данными скрытой теплоты и теплового расширения. С использованием предложенного потенциала было показано, что β-фаза титана более плотная, чем α-фаза. Основная цель разработки второго потенциала заключалась в возможности описания энергии образования точечных дефектов в α-фазе. В работе отмечено, что эта цель может быть достигнута только путем исключения данных о температуре плавления из набора параметров для подгонки параметров потенциала. Как результат второй потенциал плохо описывал температуры плавления β-фазы, но все же корректно описывал температуру фазового перехода α-β-фаз. Полученные энергии образования точечных дефектов довольно точно согласуются с данными, полученными из квантово-механических расчетов. Исходя из того, что второй потенциал не давал монотонно возрастающей зависимости параметра решетки от температуры (то есть, по сути, не описывал линейное тепловое расширение), авторами был предложен третий потенциал, который учитывал линейное тепловое расширение, однако хуже согласовывался с данными точечных дефектов в α-фазе. В цитируемой работе показано, что построенные потенциалы пригодны для описания пластической деформации, так как правильное описании энергии дефекта упаковки обеспечивает корректное описание поведения дислокаций.

В работе Д.Е. Смирновой и др. [67] предложен ЕАМ-потенциал для урана U. Сложности, связанные с моделированием урана, обусловлены его радиоактивной природой, а также большим набором фаз: орторомбической (α-фаза), тетрагональной (β-фаза), высокотемпературной ОЦК (γ-фаза) и жидкой фаз. Предшествующие работы по построению потенциалов для урана описывали, как правило, относительно небольшой спектр исследуемых свойств и были основаны на данных, вычисленных в квантово-механических расчетах. Стоит отметить, что работа Д.К. Белащенко [16] посвящена построению ЕАМ-потенциала для урана, который дает точное описание свойств жидкого урана, однако не позволяет описывать твердую фазу. Разработка потенциала осуществлялась с помощью метода «согласования сил» [34], предполагающего построение набора данных различных параметров материала, полученных из первых принципов, а затем подбор параметров потенциала и его оптимизация. При построении потенциала авторы ориентировались на свойства α-, γ-фаз, и жидкую фазу урана. Для построения справочного набора параметров использовались наборы эталонных структур, которые были получены в ходе прямого молекулярно-динамического моделирования с использованием потенциала Д.К. Белащенко [16]. Затем, используя квантово-механические соображения, рассчитывались значения межатомных сил, а также значения энергии на атом для каждой конфигурации. Для воспроизведения внутренней структуры урана использовался псевдопотенциал, предложенный в работе [49]. Все функции ЕАМ-потенциала интерполированы кубическими сплайнами. Сплайн-узлы в ходе подбора параметров потенциала корректировались итерационным способом путем минимизации отклонений между значениями, полученными в ходе квантово-механических расчетов, и значениями, вычисленными с помощью ЕАМ-потенциала. После процедуры подбора параметров проводился ряд численных экспериментов для определения тестовых структур и свойств урана. Полученные результаты сравнивались с экспериментальными данными. Если соглашение являлось недостаточным, то производилась модификация базы данных: добавлялись или удалялись отдельные конфигурации, изменялись веса конфигураций на схеме минимизации. В цитируемой работе показано, что построенный потенциал дает хорошее количественное описание структуры и свойств твердого урана. Кроме того, показано, что построенный потенциал может быть использован для описания трансформации α-γ урана.

В работе J.M. Winey [73] предложен потенциал для Al . Построение потенциала производилось по данным атомного объема [26] и упругих констант второго [70] ( SOEC – second-order elastic constants ) и третьего порядка ( TOEC–third-order elastic constants ), полученных из экспериментов [70] при комнатной температуре. Экспериментальные данные в ходе подбора параметров потенциала использовались после их экстраполяции до температуры T = 0 K с использованием классических термодинамических соотношений (квантовые эффекты не учитывались). Разработка предложенного потенциала была мотивирована тем фактом, что подавляющее большинство работ, связанных с построением потенциалов межатомного взаимодействия типа ЕАМ, не включают в себя оценки предсказания термоупругих свойств для различных термодинамических условий, следовательно, между результатами классического МД-моделирования и экспериментальными данными могут возникать существенные расхождения, ввиду того, что такие процессы, как упругопластическая деформация и фазовые переходы, определяются лежащей в их основе термоупругой реакцией материала. Разработанный потенциал сравнивался с экспериментальными данными [26], а также расчетными данными, полученными с использованием потенциалов предшественников [23, 34, 57]. Было показано, что экстраполяция экспериментальных данных до температуры T = 0 K позволяет точно описать атомный объем при более высоких температурах, что не удавалось сделать с помощью потенциалов, разработанных ранее: потенциалы [23, 34] разрабатывались на основе экспериментальных данных при низких температурах, поэтому классическое описание атомного объема при более высоких температурах является не вполне корректным, поскольку поведение измеренного низкотемпературного атомного объема отклоняется от классического высокотемпературного поведения из-за квантовых эффектов; потенциал [57] давал худшее согласование с атомным объемом ввиду того, что при построении потенциала использовались экспериментальные данные при комнатной температуре без экстраполяции.

В таблице приведена сравнительная характеристика некоторых потенциалов, предложенных в цитируемых выше работах, что позволяет использовать тот или иной потенциал в зависимости от особенностей исследования.

Сравнительная характеристика применяемых EAM-потенциалов Comparative characteristics of different EAM potentials

№ п/п	Материал	Авторы, ссылка на источник	Физико-механические свойства, хорошо описываемые потенциалом	Физико-механические свойства, плохо описываемые потенциалом, другие недостатки
1	Be	M.I. Baskes [13]	Параметры решетки и энергии связи	Зависимость свойств от температуры
2	Be	A. Agrawal [6]	Структура кристаллической решетки, радиационные свойства, тепловое расширение	Температура плавления
3	Li, Na, Cu, U	Д.К. Белащенко [15–18]	Критические температура, давление, плотность, фазовый переход первого рода, диффузионные свойства	Требуется большое количество подгоночных параметров
4	Fe (ОЦК)	М.И. Менделев [43, 54]	Структура кристаллической решетки, фазовый переход первого рода, магнитные свойства	Требуется большое количество подгоночных параметров
5	Fe (ОЦК)	B.-J. Lee [51]	Структура кристаллической решетки, магнитные свойства	Температура плавления
6	Fe	H. Chamati [21]	Структура кристаллической решетки, свойства самодиф-фузии, тепловое расширение	Требуется большое количество подгоночных параметров
7	W	M.-C. Marinica [52]	Образование и характеристики винтовых дислокаций, возникновение радиационных дефектов	Структура кристаллической решетки
8	Ni	M.I. Baskes [11]	Фазовый переход первого рода, температура плавления	Свойства переноса (коэффициенты диффузии, вязкость и др.)
9	Ni	J.E. Angelo [14]	Фазовый переход первого рода, энергия связи	Температура плавления
10	Ni	J. Cai [20]	Фазовый переход первого рода, температура плавления	Энергия связи
11	Nb	M.R. Fellinger [35]	Структурные и упругие свойства, свойства точеных и линейных дефектов	Ударно-волновое воздействие, радиационное воздействие
12	Ti	M.I. Mendelev [55]	Линейное тепловое расширение, энергия дефекта упаковки	Фазовый переход второго рода, свойства точечных дефектов в α-фазе
13	U	Д.К. Белащенко [16]	Свойства в состоянии расплава	Свойства в твердом состоянии
14	U	Д.Е. Смирнова [67]	Структура и свойства твердого урана, фазовый переход α-γ	Свойства β-фазы
15	Al	J.M. Winey [73]	Атомный объем при ненулевой температуре, тепловое расширение	Фазовый переход первого рода

Заключение

В статье приведен краткий обзор работ последних 10–15 лет, в которых предлагаются различные подходы к построению, идентификации параметров и проверке (верификации) потенциалов межатомного взаимодействия для однокомпонентных атомных систем. В настоящее время подходы к построению потенциалов, основанные на методологии погруженного атома, все более широко используются в молекулярно-динамических моделей, а последние, в свою очередь, позволяют все более точно описывать как разнообразные свойства материала, так и процессы, происходящие на уровне атомарной структуры. Используя подходы молекулярной динамики, исследователи получают количественные оценки не только параметров кристаллической решетки, коэффициентов теплового расширения или упругих характеристик металлов, но и такие важные для понимания происходящих в материале процессов характеристики, как свойства точечных и линейных дефектов, энергию дефекта упаковки и межатомных границ, характеристики фазовых переходов первого и второго рода, магнитные свойства ферромагнетиков.

Работа выполнена при финансовой поддержке гранта Президента РФ № МК-1298.2017.1.

Acknowledgments

This work was carried out with the financial support of the Grant of the President of the Russian Federation Nr. МК-1298.2017.1.