Стохастический подход к оптимизации квантованных дифракционных оптических элементов

В настоящее время дифракционные оптические элементы (ДОЭ) нашли широкое применение для решения задач управления пучками лазерного излучения в таких областях как оптическое приборостроение, технологические лазерные установки, волоконная оптика и т.д. ДОЭ представляет из себя пластинку из оптического материала с нанесенным микрорельефом, высота которого определяет локальное изменение фазы освещающего пучка [1].

Значительное количество современных технологий формирования микрорельефа использует аппроксимацию в общем случае непрерывной функции микрорельефа ДОЭ кусочно-постоянной (квантованной) функцией [2]. Это определяет актуальность построения процедур расчета квантованных ДОЭ (ДОЭ с квантованной функцией микрорельефа). Расчет квантованных ДОЭ с помощью итерационных алгоритмов типа Фьенапа [3, 4] затруднен в силу необходимости решения обратной задачи на каждой итерации. Использование стохастических процедур [5] не предполагает необходимости решения обратной задачи, т.е. поиск функции микрорельефа ДОЭ может осуществляться непосредственно над множеством технологически реализуемых функций, что дает возможность избежать погрешности квантования.

Однако построение стохастической процедуры оптимизации реального ДОЭ требует решения большого числа прямых задач, что в общем случае может привести к нереализуемым на практике вычислительным затратам.

Представляется целесообразным рассмотреть применение стохастических проце дур оптимизации ДОЭ специально для случаев, когда решение прямой задачи не требует больших вычислительных затрат (например, в случае радиально-симметричного ДОЭ или в случае если функция пропускания ДОЭ допускает разделение по координатам). Данная работа посвящена применению известной генетической стохастической процедуры нахождения экстремума функции многих переменных к расчету квантованных ДОЭ, фокусирующих излучение одномодового лазера в двумерные фокальные области в виде круга и прямоугольника.

Оптимизация фазы радиальносимметричного ДОЭ с помощью генетического алгоритма

Генетический алгоритм (ГА) - это итерационный стохастический алгоритм, который работает с набором "индивидов" (популяцией). Каждый индивид представляет собой потенциальное решение задачи. К примеру, в случае расчета радиально-симметричного ДОЭ в качестве отдельного индивида может быть определена фазовая функция ДОЭ ^ ( r ) е [ 0 , 2 п ] такого вида, что соответствующий микрорельеф

h ( r ) = ^ ( r X/( 2n ( n - 1 )) , ⁽¹⁾

где n - показатель преломления материала, X - длина волны излучения, реализуем с помощью имеющихся в наличии исследователя технологических возможностей. В случае наличия технологии изготовления бинарных (двухуровневых) элементов в качестве индивидов целесообразно рассматривать фазовые функции, принимающие в каждой точке одно из двух значений - 0 или п (или 2п и п). В общем случае расчета ДОЭ с числом уровней квантования M, фазовая функция принимает значения ф(г)е {(2nm / M): m е [1, M Ь Отметим, что если в случае использования "детерминированных" методов оптимизации [3, 4] расчет квантованных ДОЭ с малым числом уровней квантования M (M=2-8) требует дополнительных усложненных модификаций процедуры расчета, то для стохастической оптимизации уменьшение числа уровней квантования означает уменьшение мощности множества допустимых решений, и, следовательно, снижение вычислительных затрат. Перед началом работы алгоритма популяция генерируется случайным образом. Затем каждому индивиду присваивается при помощи некоторого "оценивающего" (целевого) функционала Ф(ф), мера ценности индивида ф в отношении рассматриваемой задачи. Значение Ф(ф) используется алгоритмом для направления поиска. Конкретный вид функционала в нашем случае определяется приложением ДОЭ. На каждой итерации процедуры численность популяции искусственно увеличивается за счет определенным образом вводимой операции "скрещивания" индивидов исходной популяции. Отобранные лучшие индивиды (в смысле введенного функционала Ф(ф)) используются в качестве исходной популяции для следующей итерации алгоритма. Вид функционала ф(ф(г)) определяется конкретным приложением ДОЭ и его вычисление вовсе не обязательно требует решения прямой задачи теории дифракции. К примеру, если требуется рассчитать элемент, формирующий пучок с заданным модовым распределением, вычисление функционала ф(ф(г)) потребует разложения светового поля по модам в плоскости непосредственно за оптическим элементом. Рассмотрим подробнее построение генетической процедуры оптимизации радиально-симметричного квантованного ДОЭ радиуса R. Начальная популяция представляет собой набор Ngen сгенерированных случайным образом одномерных массивов

^{{ ф} j jNL O . Каждый

мас-

сив соответствует одной реализации фазы элемента ф ( г ) , взятой вдоль его радиуса:

ф j = ф ( j A ) e { ln m / M } ,      (2)

где А = R/ ( N - 1 ) , R - радиус ДОЭ.

После генерации начальной популяции (популяции "родителей") организуется цикл, в теле которого последовательно выполняются следующие операции:

• -    скрещевание - формирование N_child дополнительных новых индивидов-массивов, значение каждого отсчета которых выбирается как значение соответствующего отсчета случайно выбранного массива-"родителя";

• -    мутация - стохастическое изменение значений случайно выбранных отсчетов получившихся новых массивов. Значение вероятности мутации p определяет скорость сходимости процедуры;

• -    селекция - определение следующей популяции "родителей" путем выбора N_gen лучших (в смысле решаемой задачи) индивидов с помощью вычисления функционала ф ( ф ) для всех N_gen + N_child индивидов.

Таким образом, на каждой итерации необходимо найти ( N gen + N_child ) значений функционала ф ( ф ) . Количество итераций N , требуемых для оптимизации фазы ДОЭ в данной работе выбиралось исходя из количества итераций, требуемых для оптимизации тестового функционала, для которого было известно значение глобального экстремума.

В качестве примера, иллюстрирующего работоспособность предлагаемого подхода, был выбран расчет ДОЭ, фокусирующего гауссов пучок в круг, что объясняется широким спектром потенциальных применений таких элементов. Выбирая функционал для оптимизации фазы ДОЭ, необходимо учесть следующие требования:

• -    адекватность функционала физической задаче,

• -    минимизация вычислительных затрат, требуемых для его реализации.

  Рассмотрим задачу синтеза ДОЭ с радиусом апертуры R для формирования из плоского гауссова пучка

  
  

  цией плоской волны на кольцеобразной апертуре [4]:

  
  

  I o ( r ) = exp ⁽- 2 r ² Jo ²)         (3)

  
  

  N-2

  w ( р ) = X

  j = o

  
  

  ^exp ( - j /°² ) е^хР ⁽ Ф _у + , ) ^{x x} ( ^rj + i J , ( к р^ , / f)/ р ^- r j

  
  

  J , ( р -/ f)/ р ) j

  
  

  фокального распределения интенсивности (рис.1)

  
  

  1 Ы', ’ ^{0 £} р ^£ R 1

  1 0 ,     р >  R , ,        (4)

  R , - радиус фокальной области. Значение где

  интенсивности 1 , может быть получено из соображения сохранения энергии:

  1 , = 7 C-C (^r ) r d r

  ^R,      0          ,          (5)

  
  

  (7) r j = j A , J , ( ■ ) - Бессель-функция 1^го порядка. Следовательно, значения интенсивности в точках р _l могут быть найдены следующим образом:

  
  

  ^{1 (}р i ) =

  
  

  или

  
  

  N-2

  X

  j =0

  
  

  ^ex p ( ^- j / ° ² ^P^, )^x

  ^{x( r},- +i J i ^{( к}р i r j + i / f)/ р i ^- r j

  
  

  J ^{( к}р i r / f)/ р l)

  
  
  
  
  
  

  C M - константа, описывающая потери Энергии, связанные с квантованием фазы по M уровням. Элемент рассчитывается как добавка к внешней сферической линзе.

  В качестве минимизируемого функционала ф ( ф ( г )) логично выбрать невязку:

  
  

  N-2

  ¹ ( р i ) = X ^ех р ^ф + , ) C j ,

  
  

  j = 0

  
  
  
  

  N , - 1

  ф ( ф ( г )) = X V (р 1 ) -1,1 ²,       (6)

  i = 0

  где N , = R , /А , - радиальный размер фокальной области в дифракционных пятнах, А , = X f J2R - размер дифракционного пятна, р , = ( i + 0,5 ) А , , 1 ( р ) - фокальное распределение интенсивности, сформированное ДОЭ с фазовой функцией ф ( г ) . Комплексная амплитуда светового поля w ( р ) в фокальной плоскости линзы может быть представлена как сумма амплитуд, образованных дифрак-

  
  
  

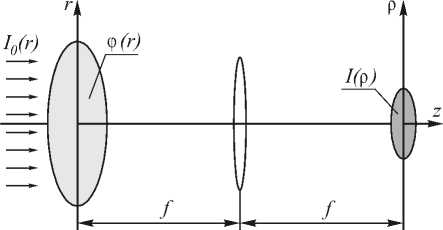
  Рис.1. Постановка задачи синтеза ДОЭ для фокусировки в круг

  
  

  где

  C j = ^e xp ^{( -} r²+ , к^{2 ) x}

  ^{x ( r}/ + i J , ^{( к} р i r j + , ! f )/ р i — r J , ^{( к} р i r / f )/ р i ) . ⁽¹⁰⁾

  Отметим, что коэффициенты C j не зависят от ф ( г ) и могут быть посчитаны до начала работы оптимизационной процедуры. После завершения работы оптимизационной процедуры подсчитывалось значение энергетической эффективности

  R1

  e = J1 (р )р Ар J 1o(r Hr

  0/ 0

  и среднеквадратичного отклонения интенсивности от среднего значения 1

  • 5 = 71 № J[1 (р)-1 ] рар ,(12)

  ¹ V ^R, 0

  2 R '

  • 1    =     J1 (р )рАр.(13)

  R,0

  Для постановки вычислительного эксперимента выбирались следующие параметры: длина волны освещающего пучка 1=10 , 6 мкм, радиус освещающего пучка 0 =1,85 мм, фокусное расстояние внешней линзы f =100 мм, радиус апертуры R =3,7 мм, радиус фокальной

  
  
  

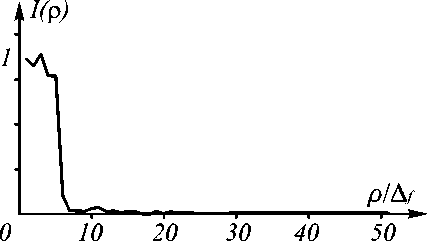
  Рис.2. Радиальное распределение интенсивности, сформированное рассчитанным

  ДОЭ в фокальной плоскости (результат численного моделирования)

  
  

  области R ₁ =0,6 мм, число отсчетов фазовой функции N =100, число уровней квантования M =4, количество итераций стохастической процедуры N t =6000. На рис.2 представлена расчетная интенсивность в фокальной плоскости элемента. Значение расчетной энергетической эффективности в ходе вычислительного эксперимента составило e = 80,3%, значение среднеквадратичного отклонения интенсивности составило 6 = 8%.

  Таким образом, применение стохастической итерационной процедуры с функционалом (6) позволяет рассчитывать четырехуровневые ДОЭ, фокусирующие гауссов пучок в круг с энергетической эффективностью, близкой к теоретическому пределу (81%), и низким значением среднеквадратичного отклонения. Отметим также небольшие вычислительные затраты, требуемые для реализации расчета элемента, что объясняется простотой вычисления функционала (6) после того, как значения коэффициентов (10) предварительно посчитаны.

  
  

  к вычислению двух одномерных [4] и, таким образом, для оптимизации фазовой функции в этом случае также целесообразно использовать стохастические методы. Рассмотрим применение такого подхода к расчету квантованного ДОЭ, фокусирующего гауссов пучок в прямоугольную фокальную область. Актуальность такой задачи объясняется широким спектром потенциальных приложений [6].

  Рассмотрим задачу фокусировки пучка с распределением интенсивности в сечении

  I₀ (u, v ) = exp ( - 2 ( u ² + v ² )/ о ² ) = = exp ( - 2 u ² / о ² ) exp ( - 2 v ² / о ² )

  в прямоугольник с фокальными размерами сторон 2a и 2b с помощью ДОЭ с фазовой функцией ^{ф (} и , v ) , определенной на апертуре D размером 2A х 2 A (рис.3).

  Определим фокальную интенсивность следующим образом:

  
  

  I = I x ■ I y ,

  
  
  
  

  где

  
  

  I x

  
  

  I y

  
  

  ^C x ^, 0,

  
  

  C y

  0,

  
  

  -a <  x <  a

  
  

  u^aчe ’

  
  

  -b <  y <  b u^aчe ’

  
  
  
  
  
  

  C x , C y - константы, выбираемые из соображений сохранения энергия:

  
  

  1 ^A

  C x =    J ^exP ^{( - 2 u} 2 / ^{о 2} N ,     (18)

  ²a - A

  
  

  Оптимизация фазы ДОЭ, фокусирующего гауссов пучок в прямоугольную область

  Отметим, что если фазовая функция элемента ф ( и, v ) и комплексная амплитуда в сечении освещающего пучка A₀ ( u , v ) допускают разделение по переменным, т.е.

  
  

  _ ф ^{( и} , v ) = Ф 1 ^{( u ) +} ф 2 ^{( v} )

  , ^A 0 ⁽ u, v ) = ^A1 ⁽ u ^{) A}2 ⁽ v )         ⁽¹⁴⁾

  
  
  

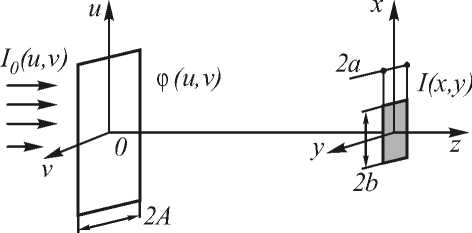
  Рис.3. Постановка задачи фокусировки в прямоугольную фокальную область

  
  

  вычисление двумерного оператора сводится

  
  

1 ^A

C y = 2ь J ^exp ^{( - 2 v 2/} ° ^{2 ) dv} .      (19)

В случае, если ДОЭ с фазовой функцией 9 ( u , v ) помещен в заднюю плоскость Фурье-каскада с фокусным расстоянием линзы f , сформированная интенсивность I ( x , у ) в выходной плоскости может быть найдена как квадрат амплитуды Фурье-образа входной комплексной амплитуды [4]:

I^y^

-^ ||е^хр ⁽-( м ² + v ² ) / ° ² ) х

2П D х exp(i9(u, v))exp(- ik(xu + yv)/ f )dudv

.

В случае расчета ДОЭ, включающего в себя линзу, формула (20) перепишется следующим образом:

характеризует качество формирования заданного распределения интенсивности с помощью ДОЭ с фазовой функцией ^ ( u , v ) .

Перейдя к дискретной модели с числом элементов дискретизации в плоскости ДОЭ N * N и шагом дискретизации в фокальной плоскости, равным размеру дифракционного пятна Д , = ёf /( 2A ) , можем заменить (25) функционалом

W ) = . ^ | ~ ( x n , Ф 1 ( u D - C xi +

N x n = 0

+ 4- Ж ( У т . 9 2 ( v ) ) - C y|        , (26)

N y m = 0

где     N_x = 2 a/Д _f   x_n = -a + п Д _f ,

У т =^{- b +} m^f , ^N y = ^2Ь I ^Д f •

~ ⁽ x>y ) =

-ik- ffexp(-(u2 + v2)/°2 )exp(i9(u,v))х 2nf“ х exp(ik (u2 + v2)/ 2 f - ik (xu + yv) f liud^

I x ( x n ) =

N - 1 z c; ^= 0

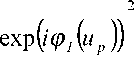
^N -I          / / V

Z C™ ^exp^i 9 2 ^{( v}q 1

q = 0

Учитывая (14), можно переписать формулу (21) в следующем виде:

I у (У т ) =

I ( x,y )=I_X ( x >1, ( у ) ,        (22)

где

^u ; = ^{- A +} ; ^Д , v q = ^{- A +} Я ^Д ,

A

~ x ^{( x} ) = ik^ff J exp ^{( - u 2} jo ² )

- A

х

C; = J^kc/2nf exp(- u2С2 )х up                              , (29)

х exp ( - ikx_nu]f + iku² /2 f ) du

х exp(г ф₁ ( u )) exp ( iku ² /2 f - ikxu / f ) du| , ⁽²³⁾

I, ( y ) =

A

7 ik/2nf J exp ( - v² Jo 2 ) х

- A х exp (i 92 (v))exp(ikv2 /2 f - ikyv / f )dv

В этом случае функционал

a

^{Ф (} ^ ^{( u , v} )) = — J |Д ( x , 9 1 ^{( u} )) ^- C x \

-a

b

⁺     J|I y ⁽ y , Ф 2 ^{( v} )) C y\ dy

2 b

-b dx +

C™ = J7 ik/ 2 П exp ( - v²/с ² ) х

, v;                                ,    (30)

х exp ( - iky ™ vjf + ikv² /2 f ) dv

Д = 2AIN • Отметим, что коэффициенты СП, Cq1 не зависят от выбора фазовых функций 91,92 и могут быть посчитаны до начала работы оптимизационной процедуры, впрочем, также как и коэффициенты Cx, Су . Для минимизации функционала (26) в данной работе также как и в предыдущем пункте данной статьи использовалась модификация известной итерационной генетической процедуры [5]. Перед началом работы итераци- онной процедуры формировалась начальная популяция, представлявшая собой набор Ngen сгенерированных случайным образом массивов

{ р j } 2N0 ¹ , р j g {( 2 nm / M ) : m g [ 1 , M ]} • (31)

Каждый массив содержал последовательно записанные отсчеты функций р 1 ( и ) ^и P 2 ^{( v ):}

P j

/   P i ( - A + jA )

ф 2 ^{( - A + ( j - N ) A )}

j < N j > N'

Для увеличения скорости сходимости в начальную популяцию вводилось в качестве начального приближения (т.е. одного из "индивидов" нулевой популяции) геометрооптическое решение р ( и , v ) задачи фокусировки гауссова пучка в прямоугольник, квантованное по M уровням. Такое решение представляет из себя суперпозицию двух одномерных фокусаторов в отрезки с длинами 2 a и 2b :

р ( u,v ) = р 1 ( и ) + р ₂ ( v ) .         (33)

Для улучшения сходимости генетическая процедура совмещалась с применением метода вариаций на каждой итерации. После завершения итерационной процедуры, следующие критерии были выбраны для оценки качества фокусировки: энергетическая эффективность

N x -1N y - 1                      /Nx - 1N , - 1

e II L k) ~ y ( y m)/ EE C x C y , (34) n = 0 m=0                   / n = 0 m=0

и среднеквадратичное отклонение сформированной интенсивности от среднего значения I

-

( Nx -1N, -1rъ

8 = ЦП, (x )I, (y . M"] ²

хШ

х

^ n = 0 m = 0

/ N x - 1 N , - 1

х

^ n = 0 m = 0

Nx -1Ny -1/

I = I I L (x ^Cym ),- (36) n=0 m=0/

Для постановки вычислительного эксперимента выбирались следующие параметры: длина волны освещающего пучка 1=10 , 6 мкм, радиус освещающего пучка 0 =1,85 мм, фокусное расстояние элемента f =100 мм, размер апертуры 2* A =6,4 мм, размер фокальной области 2 a *2 b =1,75*3,5 мм, число отсчетов фазовой функции на апертуре элемента N*N =100*100, число уровней квантования M =8, количество итераций стохастической процедуры N .=100, число индивидов исходной популяции N gen = 20 , число индивидов, образованных операцией скрещивания N chid = 20 . Уменьшение значения функционала невязки с ходом итераций показано на рис.4.

На рис.5 представлены итерационно рассчитанная фаза ДОЭ ( a ) и интенсивность в фокальной плоскости элемента: ( b ) - результат численного моделирования итерационно рассчитанного ДОЭ, ( c ) - результат численного моделирования геометрооптического приближения.

Значения расчетной энергетической эффективности (34) и среднеквадратичного отклонения интенсивности (35), полученные в ходе вычислительного эксперимента для квантованного геометрооптического приближения и итерационно найденного решения, приведены в таблице.

Таким образом, применение стохастической итерационной процедуры с функционалом (25) позволяет рассчитывать восьмиуровневые ДОЭ, фокусирующие гауссов пу-

, (35)

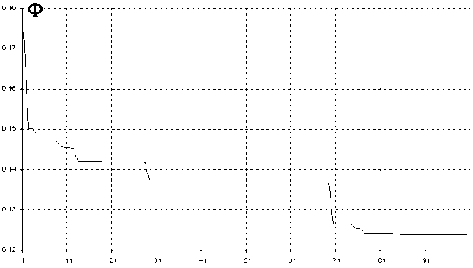
номер итерации

Рис.4. Зависимость значения невязки от номера итерации

б)             в)

Рис.5. Итерационно рассчитанная фаза ДОЭ (черный цвет соответствует значению фазы 2п, белый - 0) (a), (b) - распределение интенсивности, сформированное итерационно рассчитанным ДОЭ в фокальной плоскости (результат численного моделирования), (c) - распределение интенсивности, сформированное геометрооптическим приближением

чок в прямоугольник с энергетической эффективностью, близкой к эффективности геометрооптического решения, и более чем в 3 раза меньшим значением среднеквадратичного отклонения для выбранного набора физических параметров. Отметим также небольшие вычислительные затраты, требуемые для реализации расчета элемента, что объясняется простотой вычисления функционала (26) после того, как значения коэффициентов (29) и (30) предварительно посчитаны.

Заключение

В данной работе рассмотрено применение методов стохастической оптимизации к расчету квантованных двумерных ДОЭ, фокусирующих лазерное излучение в двумерные области. Приведенные результаты вычислительных экспериментов подтверждают перспективность применения стохастического подхода к оптимизации квантованных ДОЭ.

Таблица. Результаты вычислительного эксперимента

Метод расчета	e , %	d ,%
Геометрооптический	87	45
Итерационный	88	13