Стохастическое моделирование финансового результата перестраховщика по договору перестрахования эксцедента убытка на языке программирования Python и расчёт величины ожидаемого дефицита перестраховщика (ОДП) в соответствии с требованиями положения Центрального банка России

Начиная с 2023 года в России вступило в силу Положение Банка России от 16.11.2021 № 781-П (ред. от 22.09.2022) «О требованиях к финансовой устойчивости и платежеспособности страховщиков» (далее – Положение № 781-П), устанавливающее, в том числе, требования к расчёту резервов страховых организаций и долей перестраховщиков в них. Одним из нововведений в части расчёта доли перестраховщиков в страховых резервах является расчёт показателя ОДП – ожидаемого дефицита перестраховщика по договору перестрахования. Целью введения данной процедуры является исключение влияния на размер нормативных требований к величине капитала страховщиков договоров финансового перестрахования, т.е. договоров, условия которых построены таким образом, что при любом сценарии развития убытков финансовый результат перестраховщика будет положителен [15].

Целью настоящего исследования является разработка способа расчёта ОДП и его сопоставление с нормативным значением, что позволяет различить договоры реального перестрахования и финансового перестрахования для целей дальнейшего учёта в расчёте страховых резервов и требований к капиталу страховой организации.

Материал и методы исследования

Поскольку будущий финансовый результат перестраховщика по договору перестрахования является случайной величиной, то его прогнозирование требует применения методов стохастического моделирования [9, 10, 19]. Основным инструментарием для реализации алгоритма стохастического моделирования в данном исследовании является модуль scipy.stats библиотеки Python scipy, которая содержит все необходимые функции и методы для осуществления подбора распределения по выборке методом максимального правдоподобия, генерации случайных значений по заданному закону распределения, а также возможности тестирования статистических гипотез для оценки степени качества выбранного закона распределения случайной величины.

Основными целями создания алгоритма являются:

• 1)    Обеспечение возможности реализации оценки распределения величины финансового результата перестраховщика по дого-

• вору перестрахования и расчёта показателя ОДП по полученному распределению

• 2)    Автоматизация и универсализация данной процедуры, то есть обеспечение возможности проведения расчёта по данным любого перестраховочного договора, подаваемым на вход модели.

• 1.    Постановка задачи

Показатель ОДП в соответствии с требованиями п. 6.3.4.3.1 Положения № 781-П должен быть рассчитан для договоров непропорционального перестрахования по формуле:

ОДП = P(AP < 0)х |E(AP|AP < 0)|

ОП          ,

где АР – оценка на дату расчета ОДП функции распределения размера финансового результата перестраховщика по договору исходящего перестрахования в соответствии с подпунктом 6.3.5 настоящего пункта с учетом временной стоимости денег;

Р(АР < 0) – оценка на основе АР вероятности наступления отрицательного финансового результата перестраховщика по договору исходящего перестрахования;

|Е(АР|АР < 0)| – абсолютное значение (модуль) оценки условного математического ожидания размера финансового результата перестраховщика на основе АР, при условии отрицательного значения финансового результата перестраховщика;

ОП – сумма оплаченной страховой организацией на дату расчета ОДП страховой премии по договору исходящего перестрахования и иных платежей, производимых страховой организацией в пользу перестраховщика согласно условиям иных договоров, платежи по которым зависят от условий рассматриваемого договора исходящего перестрахования, и оценки на дату расчета ОДП приведенной стоимости ожидаемого размера еще не оплаченной страховой премии по договору исходящего перестрахования и таких платежей.

Финансовый результат перестраховщика по договору исходящего перестрахования не предопределён заранее и является стохастической (случайной) величиной. Распределение этой величины может быть получено путём осуществления имитационного моделирования множества сценариев будущих выплат по договору перестрахования и долей перестраховщиков в них [2-4, 7, 8].

Таблица 1

Условия договора перестрахования

Лейер	Приоритет	Лимит	Агрегатный лимит	Ставка пересчёта	Цена восстановления	Количество восстановлений
1	100 000	400 000	1 600 000	11,69%	11,69%	3
2	500 000	1 000 000	3 000 000	1,78%	1,78%	2
3	1 500 000	3 500 000	7 000 000	4,30%	4,30%	1

Таблица 2

Профиль риска

Сегмент	Средняя страховая сумма	Количество договоров	Математическое ожидание кол-ва убытков	Премия	Премия Re	Комиссия Re
Имущество	1 000 000	10 000	150	50 000 000	4 000 000	2 000 000
Ядерные риски	2 000 000	1 500	12	3 000 000	150 000	75 000

Наиболее распространённой в России формой непропорционального договора перестрахования является договор эксцедента убытка (excess of loss) [5, 6, 13]. В данной схеме доля перестраховщика в каждой конкретной выплате определяется индивидуально в зависимости от величины выплаты за вычетом собственного удержания перестрахователя, с учётом лимита ответственности перестраховщика по одному убытку и агрегатного лимита ответственности по договору в целом. Также может рассчитываться восстановительная премия за возобновление перестраховочного покрытия после возникновения крупного убытка. Договоры перестрахования эксцедента убытка как правило содержат деление на слои – лейеры, в рамках каждого из которых установлены приоритет, лимит ответственности по одному убытку и агрегатный лимит, а также условия возникновения и расчёта восстановительной премии.

В табличном виде условия договора перестрахования по схеме эксцедента убытка могут быть представлены следующим образом (табл. 1).

Помимо данных о договоре перестрахования для расчётов также необходимы параметры профиля риска договора перестрахования в разрезе сегментов бизнеса (табл. 2).

Также для расчёта необходимы данные о прошлых убытках страховой организации. На основе исходных данных моделируется распределение убытков по прямому портфелю, затем применяются условия перестрахования, получается распределение убытков

и сумм восстановительных премий по договору перестрахования. Далее рассчитывается распределение финансового результата перестраховщика и ОДП.

2. Этап прогнозирования

Вначале необходимо задать параметры кода и импортировать исходные данные в формате pandas-датафреймов. Фрагмент представлен на рис. 1.

Данные статистики страховых выплат прошлых лет визуализируются в при помощи библиотеки seaborn для оценки распределения тяжести по сегменту портфеля, чтобы потом использовать для моделирования аналитическую оценку (рис. 2).

По результатам визуализации можно сделать предварительные выводы относительно закона распределения величины индивидуальной выплаты, а также при необходимости отсеять выбросы в исходных данных. Для идентификации выбросов также может помочь визуализация общего массива выплат в виде boxplot и гистограммы (рис. 3).

В данном примере виден один крупный выброс.

Помимо отсеивания крупных выбросов, прошлая статистика может быть предварительно скорректирована по масштабу исходя из условий профиля риска: например, если средняя страховая сумма по договору, подпадающему под действие перестрахования, составляет 2 млн руб, а в прошлой статистике выплат средняя страховая сумма составляла 1 млн руб, то разумно будет величину выплат в статистике умножить на 2.

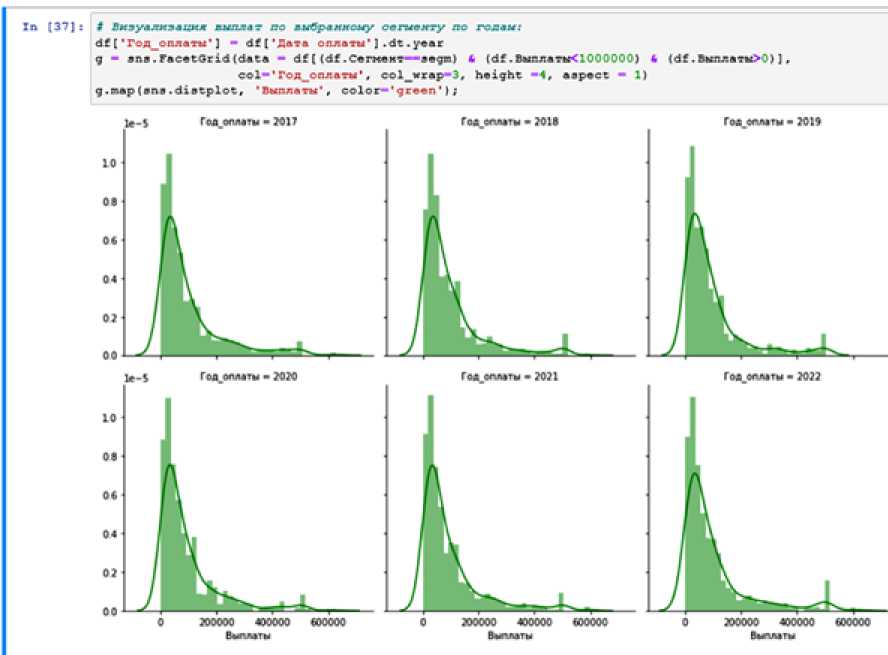
Рис. 2. Данные статистики страховых выплат

Далее для каждого сегмента бизнеса, покрываемого договором перестрахования, выполняется имитационное моделирование с разделением на две составляющие:

• 1)    Определение дискретной функции распределения количества будущих выплат и имитационное моделирование количества будущих выплат в каждой итерации. Для этой цели используется стандартное распределение Пуассона с параметром мато-жидания, равным матожиданию количества убытков, указанному в профиле риска. Данная величина может быть предварительно оценена исходя из отношения количества состоявшихся убытков в прошлых периодах к экспозиции риска за соответствующие периоды. Далее на основе заданного распределения Пуассона можно сгенерировать список количеств выплат для каждой итерации методом: Paid_quantity = list(sps.poisson. rvs(num, size=iters)), где iters – параметр, задающий число итераций, а num – матожида-ние распределения Пуассона.

• 2)    Генерация списка значений выплат в полученном количестве для каждой итерации. Если имеется достаточная статистика,

то моделирование будущих выплат может осуществляться двумя способами:

• a.    путём бутстреппинга – то есть повторной выборки величин выплат из прошлой статистики при помощи функции choices библиотеки random в количестве, равном значению списка Paid_quantity на каждой итерации;

• b.    путём генерации n случайных значений из функции распределения величины индивидуальной выплаты. Если прошлой статистики выплат не имеется, то необходимо применить актуарное предположение относительно закона распределения будущих выплат и его параметров. Если прошлая статистика имеется и она достаточно репрезентативна, то параметры закона распределения величины индивидуальной выплаты могут быть подобраны на основе прошлой статистики выплат. В результате рассчитывается распределение убытков по прямому портфелю, распределение убытков и сумм восстановительных премий по договору перестрахования, которые затем используются для расчета распределения финансового результата перестраховщика и ОДП.

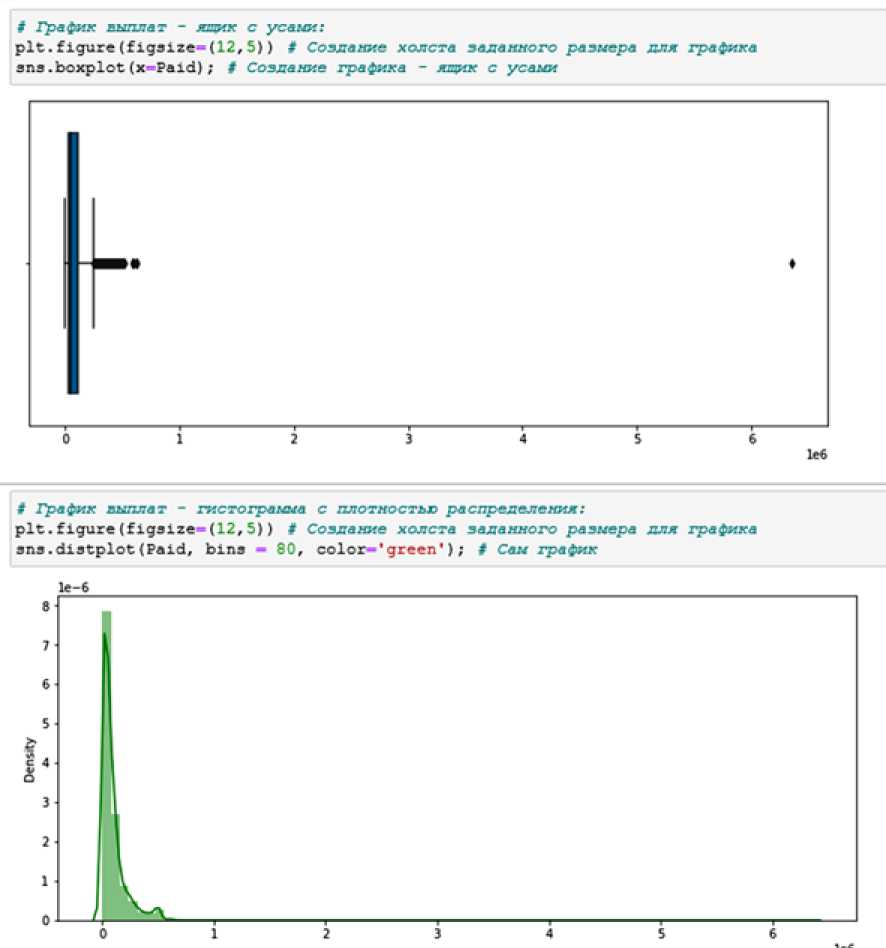
Рис. 3. Гистограммы по выплатам

* Пословреяъ список имевшихся законов распределения б коя-во параметров 6 них my_dl$trs • (d for d in dir(sps) if isinstance(getattr($ps, d), sps.rv_continuous)J print(len(ey_dlstr$)) for 1 in ey^distrs:

print(f* В распределении {1} {eval("sps*“ ♦ i ♦ "»nueargs")} параметров*)

В распределении alpha 1 параметров

В распределении anglit e параметров

В распределении arcsine 0 параметров

В распределении argus 1 параметров

В распределении beta 2 параметров

В распределении betaprime 2 параметров

В распределении bradford 1 параметров

В распределении burr 2 параметров

В распределении burr!2 2 параметров

Рис. 4. Программный код для вывода всех вариантов непрерывных распределений и количества параметров в них dUtrt • d for d la dir(ipt) if ii$A1t»rK*(t«t*ttr(»pt, d), #p4.rv_centlnuou») if гьаЦ’Н»-' • d • ’-nuaargt') in 1, 2. . ■ Mv нгпдиршвшш ia#.o** p ditto • alpha', 'Hie*, Чоках1, ‘*<1ЬиП_к1п', •doeibull", 'pareto', *l*we4bull‘] • (nuto* dwdpowwx xo«x>*>6 pocrpr**r*#a d'ffn

printff* Распределение distrtl]1 с параметрам* eval("tpt. ' • 4^trs[i| • '.flt(Peld)")>*) if eval(*$p$.' • distrs[l) • ,,'uur|f) •• 1:

• a, b, c • Ml(4pi- • dlitn 1 • ".fit(Pald)*)

GefOt .coluwtt • diitri

6#rOf.to_xK

• • aKHM^■■^^^^^^^^^^^^^^^^^^■i

  Раслредалемие alpha с параметрами (d.02954840162109363, -4171.9373116892945, 2609). 6*213179*92)

Распределение beta с лараме’ра*и (1.9435 3 3549W3W5, 8 7 Mi.39830)33606, 230.30265593413758, 7942720529.620779)

Рас^адегм 1к»х $ параметра** (6.4|)T09O?»454SW, 2)1-HW51«14>62. 5161)9.31129926544)

Расгределе-ше *e Lbw li_eln с параметрами (8.36)4456550176915, 231.56999999999996, 93)89.38972’44177)

»Pt*»eMi**e dweitwll c necewerpaw [0. T9B36 30262 76474), 4J905.90080900002. 54314.82749174441)

Раслв<д»ле*м расою e параметрами (6.475419048448260. 5178*5.3729229667. 517296.94292296845)

Распределение liwwcibull С параметрам» /*.134673*1041326414, 231.5*999965742714. 2.5343*4857565897]

Рис. 5. Программный код для подбора параметров методом максимального правдоподобия alpha.level - b.es for dlst In GenDf .colmenu tt_res_l - sp-s.ttest_lnd(6enDf dlst I ЛШпа(в), Paid) x -Зроберка гыпс«ееэ* pe6ewc«6a mwj«ui*

cheek • tt_resldj[l] < alp*ia_level print(*"Раслре*е^енме dlst check " ‘nzcxxo* • (1 - check) * ‘мороео* соотоетстеует npou.-oA статмст»<е no близости tt_res 1 ")

Раслредегение alpha пгоко соответствует лроепоА статистике по близости мето*ид*ми2

Роспроегеиие alpha плохо соответствует лроепоА статистике по блевости дислерС1нА

Распределение alpha плохо соответствует лром/»ой статистике по близости медиа*

Распределение beta xopouo соответствует проило* статистике по близости метраидамиА

Распределение beta плохо соотеетстеует проыоб статистике по близости ди с перс и*

Распределение beta плохо соотеетстеует проело* статистике по близости медиан

Распределение То*#» хорошо соответствует проело* статистике по близости метожндами*

Распределение 1ома« корове соответствует проело* статистике по близости днеперс#*

Распределение Хешах хорошо соответствует проело* с*ат*стике по близости медиа*

Раслредепенме *е1ЬмП_е$п хорошо соответствует прошло* сто**сти<е по близости метоиидани*

Распределение не1ЬоП_в$п хорошо соответствует прошло* статмстике по близости дисперсий

Распределение ме1Ьш11_*1п плохо соответствует прошло* статистике по близости медиа*

Распределение dwelbuli плохо соответствует проело* статистике по близости метож*да*г*

Распределение dwelbuli хорошо соответствует прошлой статистике по близости дисперсн»

Распределение dwelbuli плохо соответствует проалой статистике по близости медиа*

Распределение pareto хороео соответствует прошло* статистике по близости *ето*иданий

Распределение pareto хоро*о соответствует прошло* статистике по близости дисперсий

Распределение pareto хорошо соответствует прошло* статистике по близости медиа*

Распределение inweibull плохо соответствует прошло* статистике по близости метохида-нй

Распределение inv*elbi*ll плохо соответствует прошлой статистике по близости дисперсий

Распределение 1п*/ме1Ьи11 плохо соответствует прошло* статистике по близости медиан

Рис. 6. Программный код для проверки статистических гипотез

Далее можно при помощи цикла осуществить подбор параметров методом максимального правдоподобия для всех законов распределения, имеющихся в модуле scipy. stats, либо ограничить список только выбранным набором распределений (рис. 5).

Затем можно проверить качество каждого из распределений, осуществив цикл применения статистических гипотез относительно близости результатов генерации по закону распределений и исходной выборки выплат. Для этих целей могут быть использованы тест Стьюдента на проверку гипотезы о равенстве матожиданий, тест Левена на проверку гипотезы о равенстве дисперсий и тест Манна-Уитни на проверку гипотезы о равенстве медиан (рис. 6).

Таблица 3

Результат имитационного моделирования по итерациям

Итерация	Выплаты, руб.	Доля в выплатах, руб.	Восстановительная премия, руб.	Перестраховочная премия, руб.	Финансовый результат, руб.	Процент доли
1	15 576 252	1 699 648	142 054	4 000 000	2 442 406	10,91%
2	21 271 874	6 108 088	308 724	4 000 000	-1 799 364	28,71%
3	11 403 183	1 605 392	140 376	4 000 000	2 534 984	14,08%
4	14 783 366	1 605 392	140 376	4 000 000	2 534 984	10,86%
5	15 183 223	1 610 784	140 472	4 000 000	2 529 688	10,61%
6	16 806 316	1 836 106	144 483	4 000 000	2 308 377	10,93%
7	14 089 357	1 610 784	140 472	4 000 000	2 529 688	11,43%
8	12 936 967	1 736 458	142 709	4 000 000	2 406 251	13,42%
9	17 169 822	1 736 458	142 709	4 000 000	2 406 251	10,11%
10	14 573 896	1 710 432	142 246	4 000 000	2 431 814	11,74%