Стохастическое оценивание параметров нелинейных дискретных объектов на основе обобщенных вероятностных критериев

ВВЕДЕНИЕ               ПОСТАНОВКА ЗАДАЧИ СТОХАСТИЧЕСКОГО

ОПТИМАЛЬНОГО ОЦЕНИВАНИЯ

Стохастическое оценивание параметров математических моделей объектов и систем является на сегодняшний день одним из важнейших направлений современных исследований для целого ряда практически значимых областей научной деятельности человека — управления различными системами и процессами, имитационного моделирования, метрологии, приборостроения и пр. Существующие в настоящее время исследования и разработки в данной области рассматривают в основном непрерывные объекты или процессы, протекающие в непрерывном времени [1–4], при этом аналогичные вопросы, касающиеся такого широкого класса моделей, как дискретные модели стохастических систем, остаются на данный момент практически не освещенными. Кроме того, разработанные методы стохастического оценивания параметров требуют, как правило, для своей удовлетворительной реализации принятия ряда упрощающих ограничений — линейности математических моделей объектов и/или наблюдателей, нормального вида распределения помех, их аддитивности и пр. [5–9]. Ниже предлагается подход к решению задачи стохастического оценивания (идентификации) параметров моделей нелинейных дискретных объектов, позволяющий избавиться от существующих ограничений разработанных методов, а также повысить потенциальную точность процедуры оценивания за счет использования обобщенных (нелинейных) вероятностных критериев.

ПАРАМЕТРОВ

Пусть вектор состояния нелинейного дискретного объекта xk задан в самом общем случае разностным уравнением xk = f (xk-1, Ak—1, nk), (1) где f(...) — известная нелинейная вектор-функция с компонентами, допускающими обращение; xk-1 — N-мерный вектор переменных состояния на (k -1)-м шаге времени; nk — N-мерный вектор шума с известной N-мерной плотностью распределения вероятности q(nk); Ak-1 — вектор (или матрица) параметров объекта соответствующей размерности, в общем случае нестационарный.

Наблюдение для k -го момента времени z _k размерности M описывается следующим уравнением (в общем случае также нелинейным):

z k = s ⁽ x k , w k ), (2)

где s (...) — известная нелинейная вектор-функция наблюдения с компонентами, допускающими обращение; w _k — M -мерный вектор шума с известной M -мерной функцией плотности распределения вероятности g ( w _k ) . Для сокращения дальнейшей записи набор векторов сигналов наблюдения z _i ( i = 1,..., k ) на текущем интервале времени обозначим через z ₁ ^k .

В рассматриваемом общем нелинейном стохастическом случае задача стохастического оптимального оценивания текущего неизвестного векторного параметра A _k - 1 может быть сформулирована как задача нахождения его значения, удовлетворяющего некоторому вероятностному критерию оптимальности J . В качестве таких критериев, обеспечивающих максимальную (потенциально возможную) точность процедуры оценивания, целесообразно использовать нелинейные вероятностные критерии, зависимость которых от апостериорной плотности вероятности (АПВ) переменных состояния p ( x _k I z^k_x ; A _k - 1 ) в общем случае является нелинейной:

J = J Q(p(xk | zk; Ak—1)) dxk = W(AkJ, (3) X где Q — известная нелинейная аналитическая функция; X — заданная область пространства состояний.

Здесь важно заметить, что различные вариации вида критериальной функции Q позволяют охватить достаточно широкий класс вероятностных критериев оптимальности [10].

Таким образом, задача в данной постановке сводится к отысканию текущей апостериорной плотности p ( x _k | z k ; A _k - 1 ) и последующему определению текущего значения искомого векторного параметра объекта A _k - 1 , удовлетворяющего выбранному критерию оптимальности J .

где p(xk-1 | zk-1; -Ak-2) — определенная на предыдущем (k – 1)-м шаге апостериорная плотность вероятности вектора состояния объекта; Ak-2 — полученная на (k – 1)-м шаге оценка искомого вектора параметров объекта; l(xk, xk-1; Ak-1) — N-мерный вектор с компонентами, полученными в результате обратного преобразования соответствующих компонентов f (...) ; Y — якобиан преобразования от вектора переменных nk к вектору xk ; d(zk,xk) — M-мерный вектор с компонентами, полученными в результате обратного преобразования соответствующих компонентов s(...); Yd — якобиан преобразования от вектора переменных wk к вектору zk .

Тогда с учетом (4) обобщенный вероятностный критерий оптимальности идентификации параметров нелинейной дискретной системы (3) можно окончательно представить следующим образом:

J=J®

X

( x k , A k - 1 )

I h ‘( A k - 1 )

d x _k .

СИНТЕЗ АЛГОРИТМА СТОХАСТИЧЕСКОГО ОЦЕНИВАНИЯ ПАРАМЕТРОВ НЕЛИНЕЙНЫХ ДИСКРЕТНЫХ ОБЪЕКТОВ НА ОСНОВЕ КРИТЕРИЯ МИНИМУМА ВЕРОЯТНОСТИ ОШИБКИ ОЦЕНИВАНИЯ

В качестве одного из возможных вариантов критерия оптимальности идентификации J используем далее критерий минимума отклонения апостериорной плотности вероятности текущей ошибки оценивания переменных состояния объекта e _k от заданной функции на выбранном интервале ее предельно допустимого изменения — от e _min до e _max, т. е.

min J = min

^A k - 1

^A k - 1

p       p emax   emax

J... J (rk(ek) - p(ek I zk))2 dek p       p emin    emin

Известно [11], что многомерную апостериорную плотность вероятности вектора состояния x для k- го момента времени p ( x _k | z k ; A _k - 1 ) можно представить в виде

p ( x az ; A k — 1 )   '^ x . A ' /;

h ^{( A} k - 1 )

^{A ( x} k , ^A k - 1 ) =

+to +to /

= J ... J I p ^{( x} k - 1 1

-to -to X

A                                      \ zk-1; Ak-2) • q(l(xk, xk-1; Ak-1))Y Iх, (4)

x d x k - 1 • g ^{( d (} z k , x k ^{)) Y} d ;

где ek = xk - xk — вектор текущей ошибки оцени вания, xk — вектор текущих оценок переменных состояния объекта; ρ(ek | z1k ) — многомерная апостериорная плотность вероятности ошибки оценивания; rk(ek) — эталонная функция, выбираемая исходя из физического смысла и особенностей задачи идентификации конкретного объекта.

Учитывая линейную зависимость значений текущей ошибки e _k от переменной состояния x _k :

e _k = x k - x k , выразим АПВ ошибки оценивания ρ ( e _k | z ₁ ^k ) через определенную ранее АПВ переменной состояния объекта p ( x _k | z k ; A _k - 1 ):

+to +to

^h * ^{( A} k - 1 ) = J ... J ^{A ( x} k , ^A k - 1 ^{)d x} k ,

-to -to

A

p ^{( e} k I ^z k ) = p ^{( e} k ^{+ x} k I z k ; A k - 1 ).

В этом случае процедуру параметрической идентификации на основе минимизации предложенного критерия можно представить следующим образом:

min J = min

A k - 1

A k - 1

p       p emax   emax

J... J (rk(ek) - p(ek I zk))2 dek = p       p emin    emin

Как было отмечено выше, процедура оптимального оценивания текущего значения параметра, удовлетворяющего предлагаемому критерию, предполагает минимизацию функции (7) на основе известных методов оптимизации функций многих переменных, вариант применения которых рассмотрим ниже в процессе численного моделирования конкретной процедуры оценивания.

p p /x 7

emax   emax /                          д\

= min I... 1 I r k ( e k ) - p( e k + ^x k¹ z k ; A k - 1 ) I d e k .

A k - 1

p p 47

e min     e min

ПРИМЕР

Производя соответствующую замену переменных в полученном ранее выражении для АПВ параметров состояния (4) и обозначив критериальное выражение через Q ( A _k - 1 ), процедуру минимизации критерия (5) можно представить в следующем компактном виде:

min J = min Q ( A _k - 1 ) ,            (6)

A k - 1           A k - 1

Проиллюстрируем эффективность предложенного метода следующим примером с последующим сравнительным анализом полученных результатов с результатами альтернативного подхода к решению поставленной задачи идентификации. Пусть стохастический дискретный объект задан нелинейным разностным уравнением xk = f(xk-1, ak-1)+ nk = ak-1" xk-31 + nk, x1 = 1, (8)

где

p p /x 7

emax   emax /                           д\

^{n (} A _k - 1 ) = J ... J I ^r _k ( e k ) - p ( e k + x k | z k ; A _k - 1 ) I d e _k =

P .      P . X7

e min     e min

где a _k - 1 — неизвестный искомый параметр (для рассматриваемого далее модельного примера исходное значение этого параметра a _k - 1 = 1 для всех

P       P emax   emax

=J. J

p       p emin    emin

f., д . J ^{л ( е} k + ^{x k} , A k - 1 )

h * ( A k - 1 )

к                7

к ^{( k} = 1, ^ , N набл , N набл тупных измерений); n _k

— общее количество дос— шум объекта с плотно-

d e _k .

стью вероятности

q ⁽ n ) = - • π

Здесь важно отметить, что в общем случае решения поставленной задачи вектор текущих оценок переменных состояния объекта x k , входящий в (6), представляет собой некоторый оператор L от многомерной апостериорной плотности распределения переменной состояния, т. е. x k = = L ( p ( x _k | z k ; A _k - 1 ) ) и, следовательно, является нелинейной вектор-функцией от искомого параметра A _k - 1 : x k = U ( A _k - 1 ) .

Тогда критериальное выражение в (6) окончательно можно представить в следующем обобщенном виде:

Г----- qb----- _к ( n - qa )² + qb ²

(плотностью вероятности Коши) с параметрами qa = 0, qb = 0.03 .

Наблюдение переменных состояния заданного объекта осуществляется дискретным измерителем, описываемым уравнением zk = s(xk)+ wk = ck"xk.5 + wk ,

где c _k — известный параметр наблюдателя (для

рассматриваемого далее модельного примера значение параметра c _k = 1 для всех k ,); w _k — шум измерителя с плотностью вероятности g ( w ) =

1 .f— gb— П к ( n - ga )² + gb ²

(плотностью вероятности

p       p emax   emax

^(Ak-1) = J... J p       p emin    emin

(k(e k + U(A k-1), Ak-1)) de к        h*(Ak-1)        7 k .

Коши) с параметрами ga = 0, gb = 0.04.

Соответственно функция Q ( a _k - 1 ) для k- го шага

алгоритма примет вид

p /                                            x 7

emax f                                    д                         1

Q(ak-1) = J I rk(ek) - p(ek+ xk I zk; ak-1) I dek = p '

e min

(г

e max

= 1

e min

r _k ( e _k )

—

+to

J p ⁽ x k — 1 1 z 1

—to

л

л

i k ^— 1 ; « к — 2 ) • q I l ( e k + X k , X k _ч; « k _J I d x к — i

h * ( « k — 1 )

(                 Л X 1

• g I d ( Z k , e k + X k ) I

d e _k ,

7 7

(„ Л           x!

q I l ( e k + x k , x k — i ; « k — i ) I= q ( l ⁽ e k + U ⁽ « k — i ), x k — i ; « k — i ) ) = q ( e k + U ⁽ « k — i ) ^— « k — i • ^x k — 3i ) ,

Л g I d (zk, ek + Xk ) I = g ( d (zk, ek

⁺ U ⁽ « k — i )) ) = g ( z k ^— c • ⁽ e k ⁺ U ⁽ « k — i ^{)) i5} ) .

В качестве эталонных функций rk (ek ) , k = i,^,Nнабл выберем численно заданные на интервале [emin =—i, emax = i] зависимости (рис. i), удовлетворяющие очевидным требованиям к виду АПВ текущей ошибки оценивания для случая корректного (близкого к истинному) определения значения искомого параметра, а именно требованию положительной определенности, требованию расположения максимальных значений этой функции вблизи нулевого значения ошибки и одновременно достаточно небольшой величины ее интегрального значения на выбранном интервале. Отметим также, что предлагаемый вариант критерия позволяет дополнительно учитывать динамические особенности используемого метода получения оценок переменных состояния (выбор которого для данного примера обсуждается ниже), например динамику абсолютной и/или относительной величины получаемых ошибок оценивания на различных временных интервалах.

Как показали приведенные ниже результаты численных экспериментов, подобная функциональная зависимость r _k ( e _k ) достаточно эффективно обеспечивает необходимую точность и скорость сходимости алгоритма идентификации для исследуемого объекта.

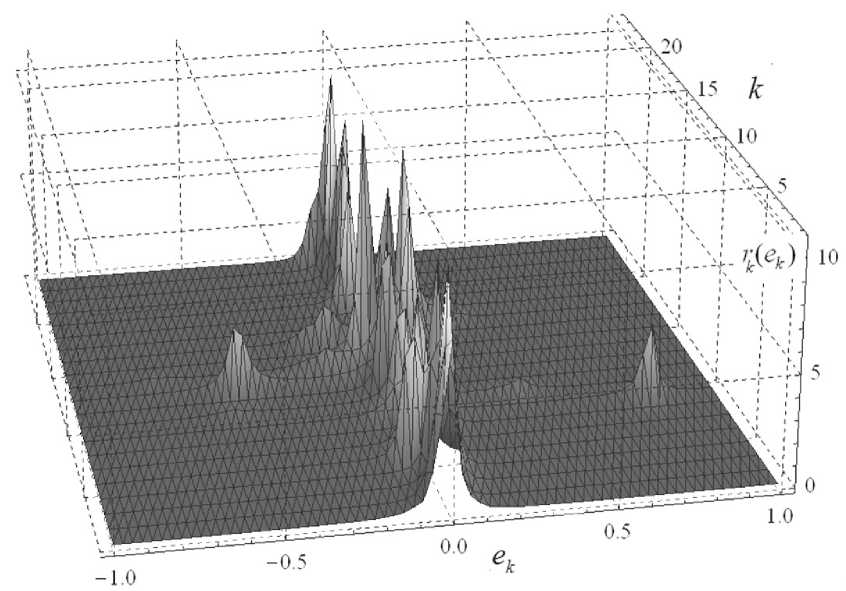
Рис. 1. График зависимости эталонных функции r_k ( e_k ) от номера k шага алгоритма идентификации.

e_k — ошибка оценивания переменных состояния объекта

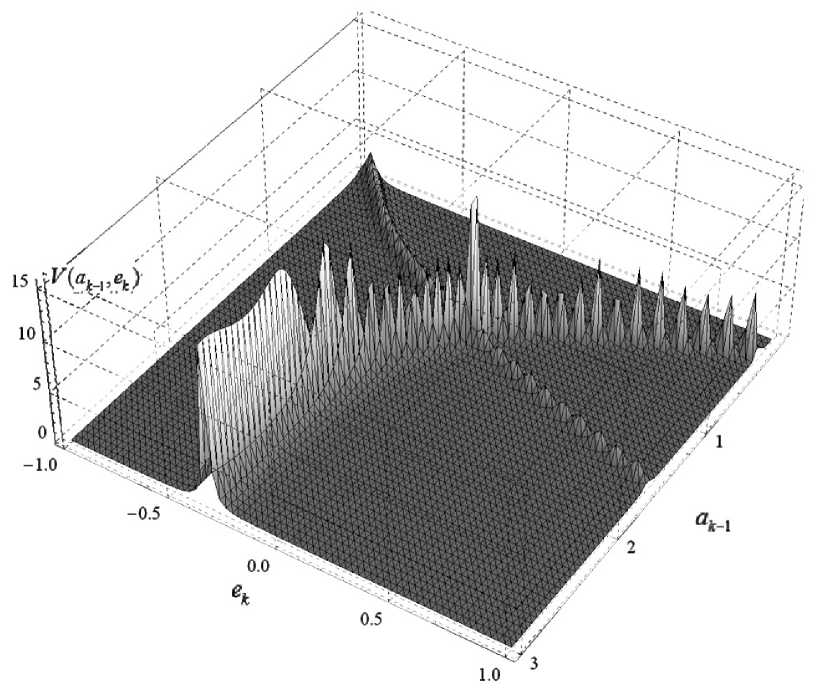
Рис. 2. Зависимость АПВ текущей ошибки оценивания V ( a k _ 1 , e k ) от идентифицируемого параметра a k _ 1 для к -го шага алгоритма ( к = 22)

Априорная плотность вероятности для первой итерации алгоритма задавалась плотностью вероятности Коши с параметром сдвига 1.3 и параметром масштаба 0.2.

Определение оценок было произведено с использованием дискретного нелинейного алгоритма калмановской фильтрации [11] при следующем выборе параметров алгоритма фильтрации: дисперсии шумов объекта и наблюдателя принимались равными D n = 0.01 и D w = 0.05 соответственно; начальное значение оценки — x 1 = 0.85; начальное значение элемента корреляционной матрицы ошибок — Л 1 = 1.

На рис. 2 представлен полученный в результате моделирования график входящей в формулу (9) АПВ текущей ошибки оценивания для k -го шага алгоритма ( k = 22), которая, являясь функцией текущей ошибки e _k , зависит в то же время от значений искомого параметра a k _ 1 ( p ( e k + x к | z kk ) = = p ⁽ e k + U ^{( a} k _ 1 ) I z k ) = V ^{( a} k _ 1 , e k )).

Определение интегралов, входящих в выражение (9), здесь и в дальнейшем производилось численно с использованием квадратурных формул с шагом A = 0.05 . Бесконечные пределы интегрирования по переменной состояния x были заменены на конечные значения, удовлетворяющие точностным требованиям к алгоритму оценивания ⁽ x min = ⁰, x max = ⁴⁾

В качестве одной из интересных особенностей графика рис. 2 можно отметить сравнительную простоту распознаваемости диапазона наиболее вероятных значений текущих оценок искомого параметра объекта, удовлетворяющих выбранному критерию, — за счет резкого изменения формы функции V ( a k _ 1 , e k ) вдоль оси оцениваемого параметра a k _ 1 . При этом сечение построенной функции вдоль оси e _k (на выбранном интервале [ e _min , e _max ]), наименее отличающееся от эталонной функции r _k ( e _k ) (а следовательно, и минимум критериального выражения (9)), располагается вблизи истинного значения искомого параметра ( a k _ 1 = 1).

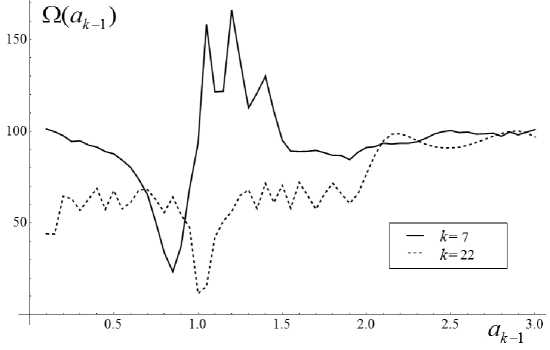
Рис. 3. Зависимость функции критериального выражения Ω ( a _{k - 1}) от искомого параметра a _{k - 1} для различных шагов k алгоритма

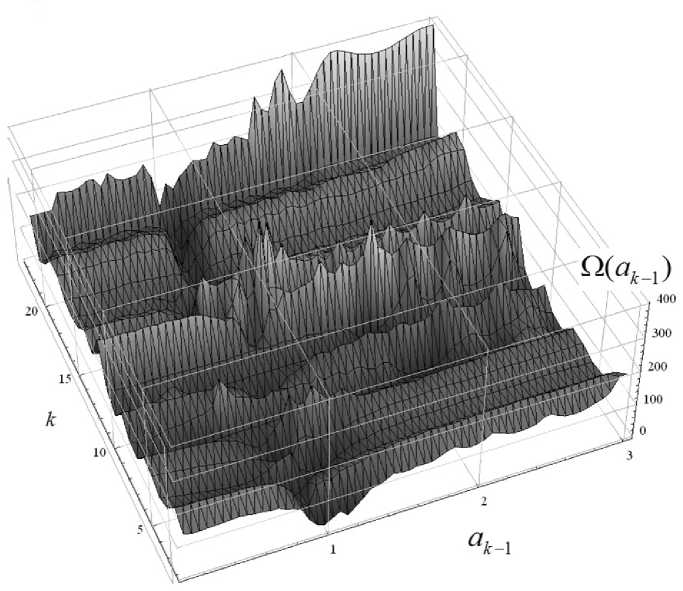
Рис. 4. График зависимости функции критериального выражения Ω ( a _{k - 1}) от номера k шага работы алгоритма идентификации

Наглядным подтверждением этого является приведенный график самой функции Ω ( a _{k - 1} ) на этом же шаге алгоритма (см. рис. 3).

Как показали результаты моделирования, вид приведенных на рис. 3 зависимостей является характерным для критериальных выражений, получаемых на различных итерациях алгоритма. Здесь важно отметить, что, имея многоэкстремальный характер, критериальные выражения на различных шагах алгоритма (при k ≥ 17) принимают свои наименьшие значения в районе истинного значения искомого параметра a _{k - 1} = 1.0 (рис. 4).

Для минимизации определенной на очередном шаге алгоритма целевой функции Ω ( a _{k - 1} ) использовался метод численной минимизации, основанный на прямой подстановке набора значений искомого параметра (заданных в интервале его возможных значений с шагом 0.05) и обеспечивающий в рассматриваемом случае достаточную оперативность и удовлетворительную точность получаемых результатов.

Результаты моделирования процедуры нелинейной параметрической идентификации показали, что при выборе количества дискретных значений сигнала наблюдения k ≥ 17 отклонение оценки

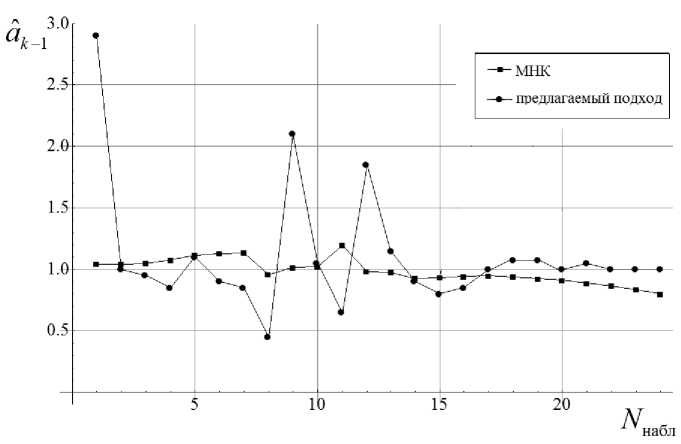
Рис. 5. Зависимости значений a k 1 оценки искомого параметра от количества наблюдений для двух рассмотренных подходов

параметра объекта a _k _ ₁ от его истинного значения a _k _ 1 = 1 не превышает 5-10 % от его величины (рис. 5).

Для анализа сравнительной эффективности предложенного подхода выберем в качестве альтернативного подхода к идентификации параметров заданного объекта (8) один из наиболее известных и широко используемых методов параметрического оценивания — метод наименьших квадратов (МНК) и сопоставим полученные результаты рассмотренных методов.

Критерий МНК, подлежащий минимизации по переменным состояния объекта и искомому параметру, в рассматриваемом случае формулируется следующим образом [13]:

E = 2 Г ( x k ^_ f ( x k _ i , ^ ) ² + ( z k ^_ ^ ( x k ) ) 2 1 . k = 1

Соответственно, расширенный вектор оценок переменных состояния и искомого параметра Aˆ , определяемый по методу наименьших квадратов, определится как x^1

v 4 = ,x ₂     = argmin( E ).          (10)

:                     ^A

x набл

Процедура минимизации в (10) производилась на основе одного из достаточно распространенных методов прямой оптимизации — метода Нелдера—Мида, показавшего наилучшие результаты из всех исследованных минимизационных процедур для данного примера. Указанный метод был реализован с использованием стандартного набора методов оптимизации среды математических вычислений Mathematica.

На рис. 5 представлены полученные в результате моделирования зависимости значений оценок искомого параметра от количества произведенных наблюдений (номеров шагов работы алгоритма) для обоих рассмотренных выше подходов.

Сравнительный анализ приведенных зависимостей показывает, что, несмотря на менее уверенную работу предлагаемого алгоритма в начальный интервал времени (при k < 17), значения оценок искомого параметра, получаемые в дальнейшем, оказываются значительно более близкими к его истинной величине, чем при использовании альтернативного подхода на основе МНК. Кроме того, приведенный график наглядно демонстрирует качественное расхождение в тенденциях изменения получаемых оценок параметров с увеличением времени работы алгоритма идентификации.

Представленные результаты исследований подтверждают принципиальную возможность эффективной реализации предложенного метода параметрической идентификации с использованием обобщенных вероятностных критериев, и в частности с использованием критерия минимума отклонения АПВ ошибки оценивания от заданной функции.

ЗАКЛЮЧЕНИЕ

Таким образом, в работе получено решение задачи стохастического оптимального оценивания параметров нелинейных дискретных объектов, обладающее рядом новых свойств:

– более высоким по сравнению с традиционными методами уровнем потенциальной точности процесса идентификации параметров за счет использования обобщенных вероятностных критериев, зависящих в общем случае нелинейно от АПВ распределения вектора состояния и позволяющих охватить широкий класс условий оптимальности;

• -    возможностью его использования при различных видах плотности распределения вероятности шума как объекта, так и наблюдателя;

• -    отсутствием ограничений на использование предлагаемого подхода также и для нестационарных неизвестных параметров стохастических объектов;

• -    принципиальной возможностью применения метода для нелинейных дискретных объектов и наблюдателей, в том числе при нелинейной зависимости функции объекта от искомого параметра.

Работа выполнена при поддержке РФФИ (грант № 10-07-00158).