Стратегия развития вуза: вариационная трактовка

The changes in a time domain of a composite organizational system (high school) are esteemed (at presence of limitations on the received administrative solutions) grounded on applying of the facilities of a variational calculus, harmonic invariants and computing geometry. The means C ++ and graphic API OpenGL conduct algorithmic implementation of an introduced methodology.

KEYWORLDS: management, organizational system, calculus of variations, computing geometry, invariants, structure of communications, goal-directed activity, model of consuming future, systems design.

Процесс управления вузом нельзя рассматривать в отрыве от внешних и внутренних факторов, влияющих на его функционирование. Их можно отнести к нескольким группам: факторы, зависящие от сложившихся в данном хозяйственном субъекте социальнопроизводственных отношений, факторы, зависящие от существующей нормативно-правовой базы и организационного обеспечения его образовательной деятельности, факторы, зависящие от положения дел на рынках труда, товаров/услуг и капитала и прочие факторы (всего n факторов) [1, 2]. Процесс эволюции вуза можно рассматривать как траекторию нелинейной динамической системы управления (далее СУ) в n-мерном фазовом пространстве (пространстве управленческих решений (далее - УР)), каждая точка которого соответствует состоянию вуза в момент времени tk. ЛПР, осуществляющему управление, приходится учитывать ограничения, налагаемые на количественные значения ее функциональных характеристик (ФХ). С геометрической точки зрения, допустимые значения ФХ задают многомерные тела (в общем случае не пересекающиеся в пространстве). Для упрощения, редуцируем n-мерное пространство УР в трехмерное и изучим деятельность вуза в этом разрезе.

Под оптимальным в данной работе понимается такое состояние СУ, при котором значение каждой ФХ, описывающей ее состояние, не может быть улучшено без ухудшения ее других ФХ (т.е., предполагается оптимальность по Парето, когда на каждом шаге управления достигается заданный с точки зрения его руководства уровень развития вуза -например по экономическим, образовательным и др. критериям). Сразу оговоримся, что эта оптимизационная задача формулируется как поиск (суб) оптимального решения. На настоящий момент существуют следующие методы ее решения [3, 4]:

Полного перебора. На ЭВМ выполняется полный перебор и оценка всевозможных значений ФХ СУ. Однако на практике в условиях метод может быть неприменим, поскольку данная задача NP-полна.

Эвристические. Менее трудоемки, эффективны для решения задач большой размерности; дают близкие к оптимальным результаты при невысокой сложности вычислений, но не обеспечивают нахождения оптимального решения. В их основе лежат опыт и интуиция (в отличие от процедуры полного перебора). Основаны на интерактивной работе ЛПР с ЭВМ и на предварительным отказе от явно неприемлемых вариантов (чем уменьшается количество подлежащих оценке альтернатив), отчего остаются лишь оцениваемые с помощью ЭВМ неясные варианты.

Определения центра тяжести. Сводится к определению центра тяжести физического тела, хорошо известному из теоретической механики. По этому методу, близкому по смыслу методу парных предпочтений В. Парето, оптимальное (но не обязательно достижимое в данный момент времени) состояние вуза соответствует центру тяжести системы, состоящей из стереометрических тел-ограничений, обладающих «массами» (значимостью для ЛПР конкретных ФХ, причем они, в общем случае, не равнозначны, что может выражаться путем введения переменной «плотности» тел). В таком случае, приемлемое, с точки зрения ЛПР, УР на данном цикле управления (в качестве цикла управления имеет смысл брать триместр, семестр или учебный год) будет заключено в трехмерном теле, полученном путем пересечения между собой тел, соответствующих ограничениям на ФХ. Далее для простоты рассмотрим случай, когда n =3.

В пространстве ценности вуза в координатах: ценность на рынке капитала, ценность на рынке товаров/услуг и ценность на рынке труда (далее, соответственно, x, y, z); ограничения, налагаемые на действия руководства вуза и зависящие от экономической конъюнктуры - состояние внешней среды, уровень организационного развития и www.rypravlenie.ru том 4 (2009), ст. 1

стратегическое видение (далее, соответственно, области А, В, С), в частном случае представляют собой стереометрические тела: параллелепипед, случай, когда ограничения задаются интервалом значений и эллипсоид

количественные характеристики принимаемых ограничения (близкий к реальности случай).

(в частном случае, сфера) - когда на ЛПР решений налагаются нелинейные Приведем аналитические соотношения,

определяющие форму допустимых областей задания УР:

• 1)    Параллелепипед С j при j =1,2,3 - случай интервальных ограничений на значения ценности: min            max

xj - xj - Xj у - yj- Ym”;

min / _ / ymax

I z j ^- z j ^- Z j

• 2)    Эллипсоид (либо сфероид) В j при j =1,2,3 – случай нелинейных ограничений (с большим x ² y ² z ²

предпочтением ЛПР значениям ценности по одной из базисных осей): — + y^- +—- = 1.

Эллипсоид получается следующим образом: ЛПР рассматривает эволюцию СУ по одной из координатным осей с учетом воздействия значащих факторов как:

x j = A j sin( ^ j t + ф j ) при j = 1, 2, 3.

где A j, to j и ф j , соответственно, допустимый диапазон изменения системных параметров, частота их изменения и запаздывание реакции СУ на управляющее воздействие. Тогда, выбирая пару координат ( x j , x k ) и исключая параметр t , имеющий смысл времени, получим параметрические уравнения эллипсоида.

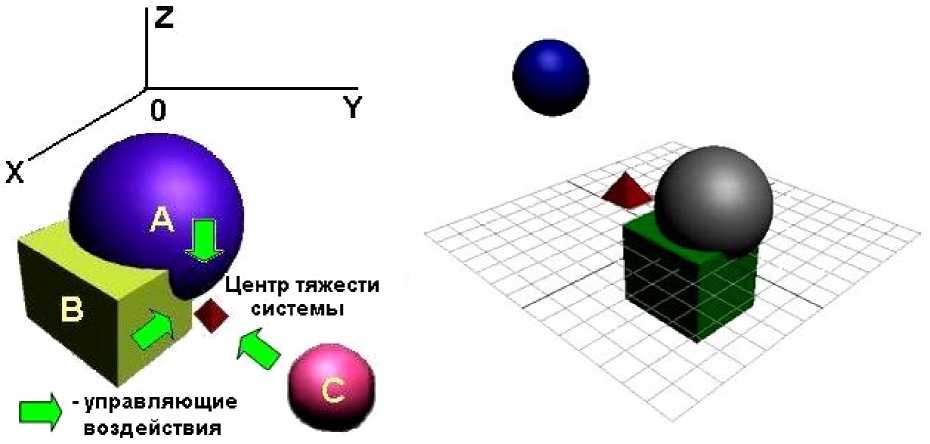
Рис. 1. Эффективное управление вузом

Сформулированные принципы геометрически представляют пересечение в трехмерном пространстве УР (x, y, z) областей реализации допустимых значений параметров

управления экономическим объектом (вузом) А, В, С — как показано на рис. 1. - ибо в рассмотрение принимается СУ, находящаяся в «гармонизированном» состоянии, толерантном относительно количественных показателей тел-ограничений. Пирамидкой обозначен центр тяжести объединенной системы, состоящей из областей А, В, С . Всего существует 5 возможных вариантов пересечения.

Количественной характеристикой пространственных тел-ограничений является их «масса», пропорциональная либо объему/площади поверхности (в зависимости от того, какая функция плотности используется: поверхностная или объемная). Устойчивое состояние моделируемой СУ на k- ом цикле реализации управления во времени будет соответствовать центру тяжести системы из трех тел. Предлагаемая методология основана на методах теоретической механики, синергетики, оптимизации и теории оптимального управления. Она была выбрана из-за ее наглядности, проработанного математического аппарата и относительной простоты ее алгоритмической реализации.

Управление состоит в том, чтобы с помощью последовательности УР на i- ом шаге (насколько это возможно) перевести вуз в состояние, одновременно удовлетворяющее допустимым реализациям А, В, С. ЛПР с помощью управляющих воздействий сдвигает тела-ограничения в пространстве УР в направлении векторов, исходящих из центров тяжести тел в направлении общего центра тяжести системы. Перевод выполняется с помощью нормативно-правовых документов и УР (точка зрения ЛПР) и с помощью применения последовательности аффинных преобразований (точка зрения системного аналитика), приводящих вуз в устойчивое (равновесное) состояние (по принципу по принципу устойчивости и эффективного компромисса Парето - точка зрения ЛПР) и в сдвиге областей А, В, С в направлении центра тяжести системы, состоящей из областей А, В, С (трактуемых как материальные точки, с массой, пропорциональной их объему - точка зрения системного аналитика).

В качестве опорной точки для принятия последующих УР выбирается центр тяжести тела, полученного пересечением областей А, В, С — области значимых решений Q : 3

Q = ^ to i , где m i - области А, В, С заданные на допустимых ЛПР интервалах. Так будет i = 1

получено объемное тело, являющееся синтетическим множеством-ограничением для системных параметров на заданном шаге управления.

Для каждой из областей А, В, С интервал их задания удобно свести с помощью масштабного преобразования к отрезку [0, 1]: ибо, так удается унифицировать www.rypravlenie.ru том 4 (2009), ст. 1

вычислительные алгоритмы и считать область определения функциональных зависимостей заданной по умолчанию.

Есть два наиболее употребительных способа выбора границ области определения границ допустимых областей значений параметров А, В, С :

1.    0 < u< 1.     2. -1 < x< 1.

Если область изменения a <  t < b , то:

t

1. u = — b

-

-

a                        2t- ba—, или t = a + (b- a)u 2. x =-------, или t = b + a + x(b- a).

a                          b — a

Эти преобразования линейны: сдвиг и растяжение/сжатие. Но применяют и нелинейные преобразования (например, потенцирование или логарифмирование) для упрощения функциональных зависимостей и учитывая особенности конкретной предметной области. Далее можно вернуться к начальным ненормированным значениям УР.

При анализе свойств симметрии и четности/нечетности функциональных зависимостей преимущество имеет второй способ. Применен первый способ, ибо характер рассматриваемой предметной области не предполагает наличия отрицательных значений свойств СУ в пространстве УР и при реализации алгоритмов наибольшая частота вычислений значений функций приходится на границы области. Далее с помощью математического аппарата вариационного исчисления будет синтезировано оптимальное управление вузом на заданном временном интервале.

Работа с объектами, заданными в пространстве УР немыслима без применения ЭВМ. Вывод изображения моделируемой СУ на экран и работа с ним, в том числе и визуальный анализ, основаны на использовании стереометрической геометрии. Геометрические соображения, подходы и идеи в соединении с возможностями ЭВМ являются одним из средств развития кибернетических методов анализа сложных СУ.

Рассмотрим графическую реализацию трехмерных объектов, ибо она тесно связана со свойствами моделируемых СУ. Система координат экрана является двумерной, поэтому на экране возможна эмуляция трехмерной системы координат, расположенной наиболее удобно для выполнения последующих расчетов. Далее все объекты считаются трехмерными, расположенными в 1 единичном октанте декартовой системы координат, а их визуализация осуществляется функциями графической библиотеки API OpenGL.

Примером практической реализации данной методологии может служить следующий: каждый объект в пространстве УР (в простейшем случае) представляет собой параллелепипед и задается в памяти ЭВМ размерами по трем осям. В его структуру входит набор специальных точек, отвечающих за соединение блоков в пространстве. В общем случае, это точка привязки и исходная точка. Получается гибкая графическая модель, позволяющая изменять размеры блоков практически мгновенно - это дает возможность реализовать графический редактор трехмерных объектов. При этом все блоки модели динамически изменяются, создавая общую графическую модель СУ. Имея графическую модель, можно реализовать движение и пересечение совокупности трехмерных объектов, что осуществляется с помощью набора функций, которые производят вращение объектов и их перенос в пространстве. В частности, для вращения каждого объекта существует алгоритм, разбивающий объект (в простейшем случае параллелепипед) на набор точек, каждая из которых вращается, используя простейшие преобразования в пространстве путем умножения матрицы радиус-вектора на матрицы преобразований в пространстве.

Кроме очевидного геометрического смысла, аффинные преобразования имеют с точки зрения экономической кибернетики еще и следующую трактовку:

• 1)    Поворот координатной системы вокруг j -ой оси на угол ф , . У вуза новое руководство, которое по-новому видит его миссию и цели управления. При этом его кадровый, образовательный и прочие потенциалы остается прежними;

• 2)    Преобразование переноса. Реализуется перевод СУ из текущего состояния в состояние желательное для ЛПР (например, для оказания нового вида образовательных услуг);

• 3)    Преобразование растяжения-сжатия (масштабирование). Выполняется пересмотр роли ценностей (проектных решений), соответствующих осям Ox, Oy, Oz (т.е. ценности на рынке капитала, ценности на рынке образовательных услуг и ценности на рынке труда) для состояния СУ в момент времени t_k , где k - номер шага управления. В зависимости от внутреннего и внешнего аспектов, учитываются изменения организационных способностей СУ.

Данные преобразования являются математическим эквивалентом инструментов «настройки» ОС и потоковых контуров ресурсов эволюционирующей СУ на состояние внешней среды и на потенциал СУ в момент времени t_k . (выполняются за время ( t_k+I-t_k )).

Область значимых экономических решений Ω получается при пересечении областей А, В, С и решается средствами вычислительной геометрии. При этом необходимо заменить выпуклую область значимых УР Ω ее приближенным аналогом – многогранником Ф (т.н. называемая линейная аппроксимация ) – см. рис. 2.

В пространстве УР (x, y, z) многогранник Ф задается набором вершин:

V(Ф) = (Vb_, V)

Центр тяжести многогранника Ф, (т.е., оптимальное УР), находится на пересечении нормалей исходящих из точек пересечения медиан каждой из граней многогранника и www.rypravlenie.ru том 4 (2009), ст. 1

направленных внутрь Ф. С практической точки зрения это означает, что при принятии УР надо, по возможности, сбалансировано учитывать влияние факторов экономической конъюнктуры

—

состояние внешней среды, уровень организационного развития и

стратегическое видение (т.е., быть на равном расстоянии от характеристических значений перечисленных факторов экономической конъюнктуры, геометрически соответствующих центрам тяжести областей А, В, С).

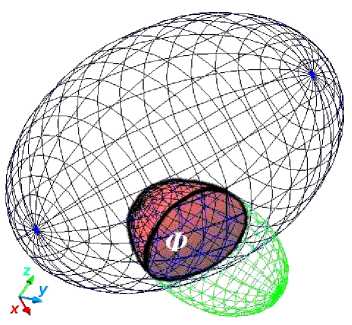
Рис. 2. Аппроксимация поверхности

Как известно из механики, приближенные координаты центра тяжести объемного однородного тела определяются по следующим соотношениям [4]:

xc

n

Е xkА vk k=1

V

,

yc

n

Е УкА vk k=1

V

,

zc

n

Е zkА vk k=1

V

,

где А v_k - объем k- ого элемента тела,

x k ,

y k , Z k - координаты точки приложения силы

n тяжести к этому элементарному объему, V — объем всего тела: V = Е Аvk .

k = 1

В нашем случае удобнее воспользоваться другой формулой. Координаты xk, yk , zk центра тяжести С однородной поверхности (с поверхностной единичной плотностью) задаются приближенно следующим образом:

xc

n

Е xk ^ k k = 1

S

,

yc

n

Е УкА sk k =1

S

,

zc

n

Е z k ^А s k

7=1 . , где

А _k — площадь поверхности k- ого

элемента тела,

x k , У к , z k

—

координаты точки

приложения силы тяжести к к- ому элементарному объему, 5 — площадь поверхности всего

n тела: 5 = ЕАk .

k = 1

Посредством графического API OpenGL [5] удается по набору вершин многогранника Ф вычислить как площади его отдельных k -ых граней, так и координаты их центров тяжести. После этого легко определяются координаты x_k , y_k , z_k многогранника Ф. Для построения траекторий оптимального управления вузом на протяжении заданного периода времени надо строить сечения многогранника Ф секущей плоскостью, проходящей через его центр тяжести. Тогда сечение Ф есть плоский многоугольник.

Предполагается, что социум, его экономические взаимоотношения и окружающая среда подчиняются общим принципам развития, а конкуренция является средством достижения равновесного состояния в природе и в экономической среде [7].

Как аналог социума (и как его миниатюрной модели – вуза) можно рассмотреть термодинамическую систему в виде твердого кристаллического тела, находящуюся в метастабильном состоянии. Как и подобные тела, социум состоит из отдельных частиц (экономических субъектов), имеющих свое уникальное (динамически изменяющееся) расположение. Все субъекты-частицы взаимодействуют со своим окружением, через обмен энергией (ресурсами), причем объем накопленной энергии и у социума и у твердого тела ограничен. Под потребностью термодинамических систем понимается необходимость снижения их свободной энергии. Твердое тело вынуждено претерпевать изменения - по принципу минимума свободной энергии. Твердые тела могут по-разному и с различной эффективностью понижать свою энергию [8].

Удовлетворение социумом своих потребностей – мера вынужденная, определяемая естественными законами природы. Ограниченность имеющихся ресурсов, необходимых для реализации стратегий вузов, заставляет их конкурировать между собой. Поскольку в борьбе за нишу на рынке побеждает игрок, удовлетворяющий максимум потребностей с использованием минимума ресурсов, конкуренцию можно трактовать как принцип достижения устойчивого равновесия (стабильности) в СУ.

Начальное значение состояния СУ (предприятия) на k -ом цикле управления в момент времени t k . (то есть начальные значения состояния внешней среды, уровня организационного развития и стратегического видения) задаются ЛПР на основе анализа доступной ему информации о вузах-конкурентах и содержатся внутри этого многогранника в виде точки R_n^k . Аналогичным образом строятся и прочие сечения.

Построив по трем точкам сечение этого трехмерного тела, получим плоскую «область-мишень», сквозь которую должны проходить допустимые траектории управления вузом во время tk; аналогично поступим и в момент времени tk+1. Выбрав в «областях- мишенях» две точки, соответствующие настоящему и желаемому состоянию системы, соединим их кривой и, вращая ее относительно прямой, соединяющей центры масс двух соседних тел-пересечений, построим тело вращения, обладающее минимальной площадью поверхности - это соответствует основополагающему принципу минимума потенциальной энергии, ибо так удается сконцентрировать ресурсы СУ на нескольких приоритетных направлениях его эволюции. Кроме того, так обеспечивается сходимость процесса перевода вуза из текущего состояния в заданное в несколько циклов управления, что дает возможность построения функции Ляпунова [6].

В качестве длительности к -ого цикла управления ( t_k+1-t_k ) на среднесрочную перспективу можно взять триместр, семестр, либо учебный год. Далее в рассмотрение будут браться пары сечений многогранников, соответствующих к -ому и ( к+1) -ому циклам управления. Нахождение траекторий эволюции, переводящих СУ из его заданного k- ого состояния в заданное ( к+1) -ое состояние осуществляется далее посредством математического аппарата вариационного исчисления.

На процесс эволюции вуза влияют факторы внешней среды и его организационный потенциал. Для предлагаемой методологии ( n =3) предполагается, что на изучаемую СУ оказывают влияние ЛПР, сгруппированные по принципу принадлежности их к определенному рынку:

• -    капитала (ось ОХ) - государство, учредители , инвесторы , менеджмент, студенты и др.;

• -    образовательных услуг (ось OY) - государство, учредители, менеджмент, студенты и др.;

• -    труда (ось OZ) - государство, собственники, менеджмент, ППС и УВП.

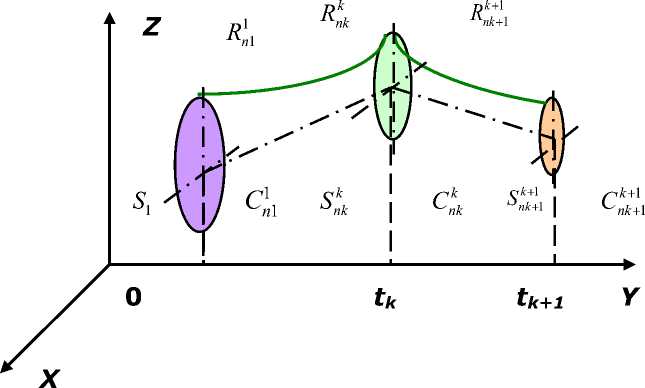
Рис. 3. Гармоничное развитие вуза

В работах А.А. Богданова по теории открытых систем, Н.Д. Кондратьева по теории длинных волн, в трудах Л.Н. Гумилева по этногенезу, в работах Дж. Форрестера,

К. Фримена, У.У. Ростоу, Й. Дельбеке [9–12] показано, что мировая экономика (в т.ч., и экономика образования) развивается циклически – за подъемом следует спад, потом опять подъем и т.д. Процессы в экономике, имеющие априори неизвестный характер, могут быть приближены суммой некоторых функций (т.е., путем разложения в ряды Фурье).

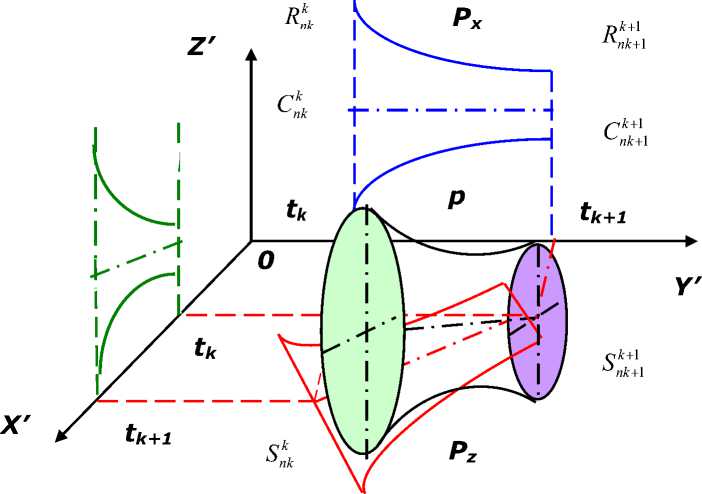
Рис. 4. Проекции траектории развития вуза

На показатели функционирования СУ оказывают влияние процессы, имеющие различный период их реализации. Возникает вопрос о выделении интересующего ЛПР временного промежутка, за который он будет осуществлять анализ СУ и последовательно реализовывать программу по достижению стратегических целей, стоящих перед СУ (и инкорпорированным в нее ЛПР). Поэтому предлагается рассматривать период в T лет (т.н. промышленный цикл СУ). В пространстве УР в координатах ( x, y, z ) процесс гармоничного развития вуза дан на рис. 3 и 4.

Каждому сечению Snk многогранника Vnk соответствует время tk, когда должен быть реализован k-й цикл управления. Закрашенные области {Snk } соответствуют областям допустимых значений параметров СУ в момент времени tk. Центрам тяжести Cnk многогранника Vnk соответствует равновесное (сбалансированное с точки зрения соблюдения ограничений) УР, которое может быть принято в момент времени tk (но которое едва ли будет достигнуто на практике). Здесь Rnk – фактическое состояние СУ в момент времени tk.. С помощью применения методов директивного управления можно постепенно сблизить Cnl и Rnl на некотором шаге управления l. При этом должны быть заданы значения

C^k „ , R k , C k ^{+ 1}, R k ^{+ 1} в моменты времени t_k и t_k+1 , соответственно.

n k ^J n k        n k + 1 n k + 1                             ^A

Так исходная задача оптимального управления к последовательному решению вариационных задач на заданном отрезке времени. Cчитается, что на каждом шаге можно рассматривать вариационную задачу с закрепленными концами – состояние СУ (вуза) в конце отрезка времени задано, ибо для него начальные и исходные значения параметров определяются по нормативным актам Минобразования РФ, которые не очень часто пересматриваются (по сравнению с длительностью шага управления). Сразу оговоримся, что это допущение с математической точки зрения является довольно сильным условием и применение его обусловлено спецификой рассматриваемой предметной области.

Из практических приложений фрактальной теории следует [14, 15, 17, 19], что в поведении открытых систем прослеживается наличие т.н. гармонизирующих инвариантов, соответствующих рядам Фибоначчи и принципу «золотого сечения». Имеет смысл выбрать отношение расстояний x= Ck Rk / Ck+1 Rk+1

^{1                     л} nk n k n k + i n k + i

постоянным для всех значений k и принять его

равным (V5 + 1)/2 « 1,41... Выбор такого значения x обусловлен тем, что количественные характеристики многих реальных эволюционных процессов связаны с рядом Фибоначчи (и с «золотым сечением» [16, 18]). Так удается достичь приемлемой для данного практического случая скорости сходимости конкретного УР, принимаемого ЛПР, к оптимальному УР для момента времени t k . При этом должно выполняться условие убывания площади сечений { S_n^k } - в предельном (идеальном) случае, ЛПР все равно примет единственное УР, соответствующее точке в пространстве УР. Искусство управления состоит в том, чтобы из всех возможных вариантов эволюции СУ в момент времени t k , выбрать наиболее «жизнеспособное». При этом возможности прогноза ЛПР ситуации, связанной с функционированием СУ, по мере увеличения t k относительно точки привязки по времени будут уменьшаться (пусть даже ЛПР и применяет принцип пошагового оптимального управления) – поскольку он движется из настоящего в будущее. Для синтезированного математического аппарата это состоит в последовательном уменьшении площади сечений { S_n^k } при возрастании t k . При этом асимптотическое поведение последовательности { S_n^k } следующее: lim _к^„ S^k_k ^ 0 .

Однако для случая такой СУ как вуз, шагов управления k не будет очень много, ибо:

• •    для получения своевременной информации о состоянии рынка образовательных услуг понадобятся подробные и затратные маркетинговые исследования, которые можно и нужно проводить не чаще чем раз в квартал (триместр), а то и реже;

• •    такая СУ как вуз обладает значительной инерционностью и не будет мгновенно и плавно реагировать на слишком частые и резкие управляющие импульсы, подаваемые ее руководством;

• •    экономическая ситуация в экономике РФ отличается турбулентностью.

Данные факторы ограничивают горизонт практического планирования мероприятий по развитию вуза 2-3 годами (т.е., глубина управления на практике - около 10 шагов-триместров), отчего применение метода рядов Фибоначчи видится вполне оправданным.

Из состояния к в состояние к+1 СУ надо переводить по возможности плавно, без резких изменений количественных значений ее функциональных характеристик (см. рис. 5а). Если воспользоваться методами теории оптимального управления, то перевод СУ из состояния к в состояние к+1 будет осуществляться в пространстве фазовых переменных ( х, у, z ). Для проблемы гармоничного развития СУ (УР принимаются в сравнительно узком «русле» стратегического видения эволюции вуза см. рис. 5б) принцип минимизации свободной энергии соответствует минимизации объема тела вращения, получаемого вращением кривой p=p(x, у, z, t) c заданными граничными точками вокруг к -ой оси, соединяющей центры тяжести С ^ и С +1 многогранников V nk и V +J .

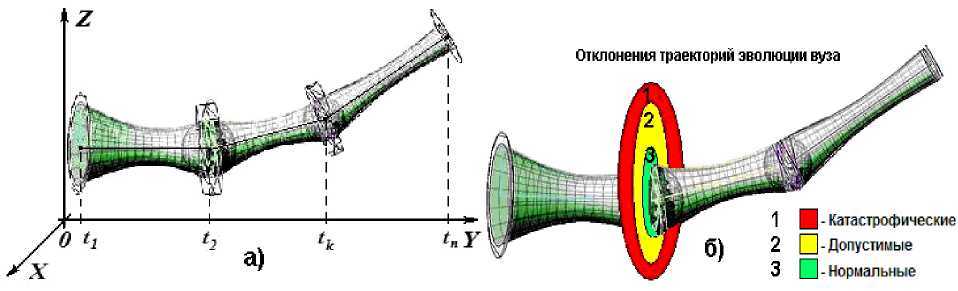
Рис. 5. Пучки траекторий управления вузом:

а) допустимое управление б) классификация отклонений траекторий эволюции СУ

Имеет смысл упростить решение этой задачи, рассмотрев три проекции кривой p=p(x, у, z, t) (соответственно, p z , p y , p_x, на плоскости Ox у, Ox z, Oy z ), и решить для каждой из них задачу о нахождении минимума функционала, соответствующего площади поверхности вращения, полученной вращением кривых p z , p y , p_x вокруг проекции к -ой оси, соединяющей центры тяжести С^к и С ^ + 1 многогранников V ^ и V + 1 (см. рис. 4).

Ее решение - катеноида, задаваемая уравнениями в проекциях на оси Ox y, Ox z, Оу z :

' p _kd= d ^kj* ch (( t _k - d ₂ ^kj )/ d j )

< Г к ,j= d j * ch (( t k - d 2 ^k j )/ d kj ) при j = 1, 2, 3 , где R ^ =( г^ Г к,з ) , R'^ Г к+1,Ык+12 , Г к+13 ) (1) _ Г кj d j * ch (( t k + 1 - d 2 ^k j )/ d kj )

Выбор в качестве траектории управления катеноиды вызван еще и тем, что переход СУ заданного ЛПР состояния R k в состояние R , ⁺ 1 за период времени ( t_k+1-t_k ) неизбежно связан с временным ухудшением ее экономических показателей (поскольку при этом применяется новая ( к+1) -я стратегия управления, неизбежно требующая от ее исполнителей время на освоение и на эффективное внедрение [13]). Постоянные { d kj } и { d kj } для линии p=p(x, y, z, t) находятся из условия (1) ее прохождения через заданные граничные точки R ^k и R^k_n ^{+ 1}. Решив систему из шести нелинейных уравнений относительно { d kj } и { d kj }, получим уравнения линии:

P k , j = ^d М * ^{Ch ((} t k ^{- d} 2 k j )/ ^d kj ). t k + 1 = t k ^{+ h} , ^h = const , tk - d k

^   Гк    dkj* ch ((tk - dkj)/dkj ) ~ d kj(1 + 0.5 * ( k    2 j )2) при j = 1,2,3, d 1 j t,.. - dk, „

Г к + 1,j = d kj * ch (( t k + 1 - d kj ) / d kj ) « d kj (1 + 0.5* ( ^{k + 1} к j ) ² ).

d 1 j

2      4

x ² n

--+ ...

(2 n )!

xx

При этом было использовано усеченное разложение ch ( x ) = 1 + — + — + ... +

Примем, что d kj = §jh, где ^j - параметр выбранной математической модели (это tk - dkj tk всегда возможно). Введем новую переменную: ^ =----— = — jk d 1 j степенные ряды для искомой траектории управления примут вид:

—

j

d kj

. Разложения в

P k , j = d kj * ch (( ^ j ) , t k + 1 = t k + h , h = const ,

Г к ,j = d kj(1 + 0.5*( ^ j )²)

при j = 1, 2, 3,

Г к + 1, j = dk, (1 + 0.5*( ^ j + - h ^)² ) = d kj (1 + 0.5* ( _V j + -¹) ² ). d 1 j                                 ^ j

Выразив d kj. = t k - Ф j ^ j h и учитывая, что Г к j = ^ j h + 0.5* ^ j h ф j , получим:

Ф з

± ²( Гк2- j )

1   ^ j h

и, следовательно, d kkj = t_k + ^2 ^ j h ( г₂ , j - ^ j h ).

Отсюда, соотношения для проекций цепной линии имеют вид:

t - 1 ₀ + J2 ^_;. h ( г₂ j - ^ j h )

p_k . ( t ) = ^ h * ch ((-----------------,--------),       h = const ,     ^ = const ,     j = 1, 2, 3. (4)

^k , 3-   ^j3                 j                               j

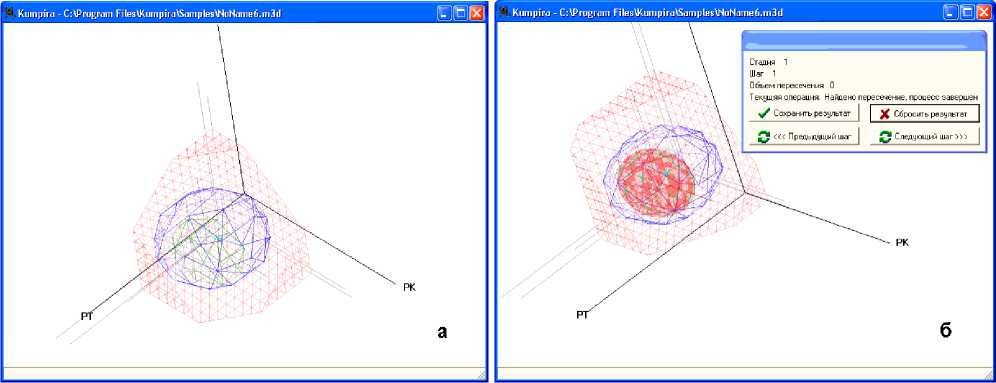
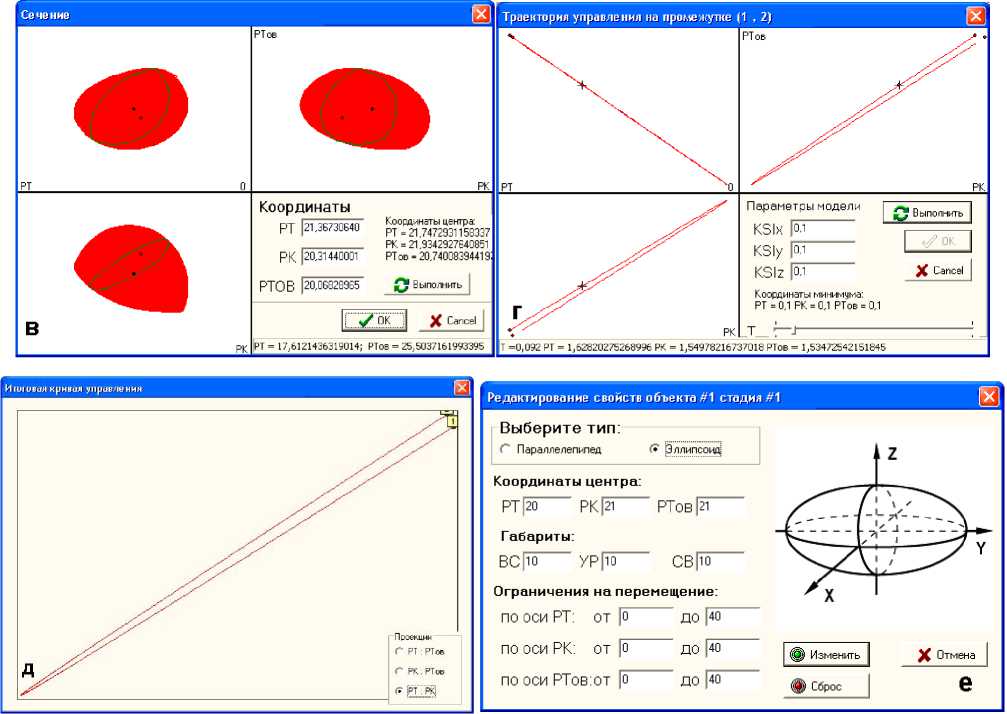
Рис. 6. Примеры работы системы Kumpira:

а) генерация объектов              б) генерация пересечения

в) построение сечения                г) построение траекторий управления

д) построение итоговой траектории     е) редактор объектов

На основе вычислительного эксперимента с выбором различных модельных параметров 5, [17, 18] получаем несколько возможных вариантов управления вузом за период времени (tk+1-tk), из которых ЛПР выбирает лучшее на его взгляд УР. Далее, задав значения R0, C0, R1, и C1, ЛПР может предложить стратегию оптимального (в рамках разработанной методологии) управления вузом на период времени (tk+1-tk). Нахождение аппроксимированного многогранником из триангуляций каждого тела-пересечения, его центра тяжести, плоских сечений и коэффициентов катеноид с визуализацией пошагового управления ведется с помощью системы Kumpira (реализованной на ЯП С++ и средствами графического API OpenGL [5]). Примеры работы системы Kumpira приведены на рис. 6 а, б, в, г.

Автор выражает признательность д.ф.-м.н. Ю.Г.Сметанину д.э.н. М.Ф.Мизинцевой и проф. В.А.Бекмурзаеву, с которыми на различных этапах создания обсуждалась данная методология, а также аспиранту С.А.Кубасову, принявшему участие в ее алгоритмизации.