Стратегия сегментации объекта на цифровом изображении

В [1-4] предлагается математическая постановка задачи сегментации:

Пусть задано P={р 1 , р ₂ , ... , p n } - конечное множество элементов плоскости изображения (модели), иконические признаки которых отображены функцией f ( а ), а также предикат LP, определяющий правило сегментации f ( а ).

Для детерминированной модели решением задачи сегментации f ( а ) является разбиение P на Л = { 5 1 , s ₂ , ..., s j непустых связных областей, для которых LP принимает истинные значения тогда и только тогда, когда любая пара элементов из любого подмножества s i ∈ S удовлетворяет цели. В альтернативных условиях обычно целью является оценка динамики изменения плотности распределения.

В общем случае сегментацию можно рассматривать как

Seg: fа) -—■ SSem\ где Л(Sem•) - семантические отношения.

В частности, s i ^{( Sem} •⁾ - имя области s i e Л , а LP ( s ,^Sem ) - указание на модель соседства, характеризующую объект.

Удовлетворительный результат сегментации при заданном множестве Л является идеальным случаем и подходит для «классического» синтаксиса детерминированного отображения вида:

• 1)    модель позволяет априори задать значение иконической функции f ( а ) для области «фон». Область «фон» заполняет все изображение, в котором расположены области Л , представляющие свойства объекта. Область «фон» характеризуется наиболее контрастным значением яркости относительно сегментируемых областей, обычно близким к максимальному или минимальному значению;

• 2)    сегментированные области s i имеют отличия по унарным признакам (обычно по градиенту: V f ( а )) и соседству, то же справедливо относительно области «фон». Т.е. области имеют границу в виде замкнутого контура.

В детерминированных условиях работа правила LP представляет собой комплексную оценку «расстояния» (близости) Vf ( а ) текущего p i eP и соседства (смежности) некоторого p j es i вида

I р:^аа ) - s , I ^ min. , и р , A p j =1, где p_jes , .                                     (1)

Так, всякий текущий р , е P относится только к одной области s , e S . Соответственно, сегментация выполняется на основе однородности и связности р , .

Вне идеальных условий отображения свойств объекта возникают закономерные нарушения формы сегментированных областей за счет искажений в виде незаконченных, ложных, утолщенных контуров, «наложения» областей и иных известных ошибок [1, 5, 6].

Один из способов борьбы с ошибками - модернизация правила (1) семантической составляющей как настраиваемого «радиуса», что позволяет улучшить качество сегментации. Такое правило имеет следующий вид:

I р, : V f ( а ) - LP ( s ^Sem ) I < r ^Sem и р , A p j =1, где p j es , ,                                 (2)

где r Sem - радиус однородности для s Sm .

Так, оценка однородности класса может быть изменена в процессе сегментации [6, 8] путем изменения r i^Sem относительно анализа однородности смежных классов. Кроме этого, может быть выполнена корректировка мощности S на основе анализа однородности s_i ^Sem и мощности области «фон».

Использование принципа адаптации (2), с одной стороны, улучшает качество, а с другой – закономерно ограничивает возможности применения правила LP ( s Sem ) для работы систем анализа изображений с иными свойствами. Причем LP ( s Sem ) обычно представляет собой априорные знания [9-12], основанные на иконической информации, что ограничивает практическое использование формализации [1-4] в решении задачи сегментации.

Стратегия сегментации

Предлагаемая в статье концепция стратегии сегментации основывается на предположении о семантической скудности отношений соседства, предоставляемых иконическим уровнем цифровой матрицы изображения, применение которой приводит к закономерным ошибкам. Поэтому полагается, что влияние ошибки и цели сегментации минимизируется при переходе к более сложной семантической модели отношений соседства, характерных свойству объекта.

В работах [13-15] выделены основные формы синтаксических отношений соседства, характерные для области изображения.

Для области изображения [13]:

• 1.    «Вырожденная» область s , I =1:

• 2.    «Область» s_i I> 1:

• 3.    «Многосвязная область» ! S i |> 1:

s01 = < Рь b,1 и b42 >, где b,1 - унарный признак области (р,); b42- отношение соседства граничных элементов (дополнения) области вида b42= < (р, о M) >, где M – множество пикселей области «фон».

sio = < Р,, {b,}1 Иb 1-bз, b5}2 >, где bi1 – признак области si включающей подмножество Рi; b12–b32, b52– отношения соседства граничных элементов области вида b 12 = < (Pi = Si n Sy) >, b22 = < (Pw"= Si П Sj) >, b32 = < (Pw*= Si n Sy) >, b52 = <(Pw = Si П Sj)>, где Pw – мощность множества граничных пикселей области.

s 11= < Pi, M*, {b} u b62 >, где bi1 – признак области si, включающей подмножество Рi; M* – подмножество пикселей области «фон»; b62– отношения соседства граничных элементов области вида b62= <(Pw = Si n M*)>, где Pw – множество граничных пикселей области.

В качестве содержания отношения соседства bi2 предлагается использовать один из функционально-параметрических признаков Фримэна [1]:

^ r = r i /r

max ,

где r i – текущие расстояние от «центра тяжести» области до граничного пикселя; r max – максимальное расстояние от «центра тяжести» области до граничного пикселя.

Характеристика функции ^ _r позволяет оценить топологическую особенность формы выпуклости области (рис. 1).

В качестве унарного признака граничных пикселей предлагается использовать значение Vf ( а ) как правила выполнения низкоуровневой сегментации области на изображении. Соответственно в качестве правила высокоуровневой сегментации – такой признак, как выпуклость формы области отображающей свойства объекта.

Таким образом, сегментация, в основу которой положен анализ однородности амплитудной характеристики отношения соседства области, позволит избавиться от закономерных оши-

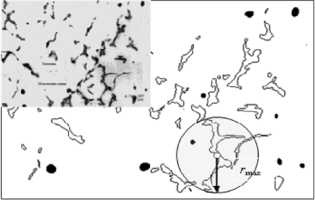
Рис. 1. Функционально-параметрическая оценка эвтектики, расположенной вблизи дефекта микроструктуры

Fig. 1. Functional and parametric evaluation of a eutectic located near the defect microstructure бок в выделении части изображения на основе иконической информации, наполняя правило LP смыслом, характерным объекту.

Эксперимент

Целью эксперимента являлась сегментация части изображения, представляющей свойства объекта. В качестве свойства рассматривался металлографический дефект микроструктуры.

В работах [16-19] отмечается, что микроструктура образцов, вырезанных на расстоянии 300 - 500 мкм от микротрещин, отличается от исходной структуры количеством и размером объектов (до 80 %). Отмечено, что по мере приближения к микротрещине происходит изменение не только формы эвтектики (она становится менее выпуклая и вытягивается), но и ее расположения (повышается концентрация, наблюдается четкая ориентация скопления) [13, 20-24].

В качестве данных эксперимента использовались эталонные микроструктурные металлографические изображения деформируемого алюминиевого сплава АМr6, удовлетворяющие ранее описанным условиям синтаксиса.

На восходящем этапе сегментации применяли метод пространственного дифференцирования. В автоматическом режиме выполнялось выделение областей эвтектики относительно оценки функции ξ _r и связности пикселей соответствующей модели «область» ( b ₄ ² ). В результате низкоуровневой сегментации были сформированы цепочки (подмножества) граничных пикселей P_w ∈ s_i с характерным значением ∇ f ( а ).

В задачу нисходящей сегментации входила выработка принципа определения оптимального радиуса правила LP ( s_i ^Sem ) с целью сегментации части изображения с характерной однородностью свойства объекта. В результате оценка плотности ξ r (изрезанности границы) позволила сформировать классы областей изображения с характерными свойствами, присущими развитию дефекта.

На рис. 2. представлен результат работы стратегии, позволяющей наглядно оценить динамику дефекта.

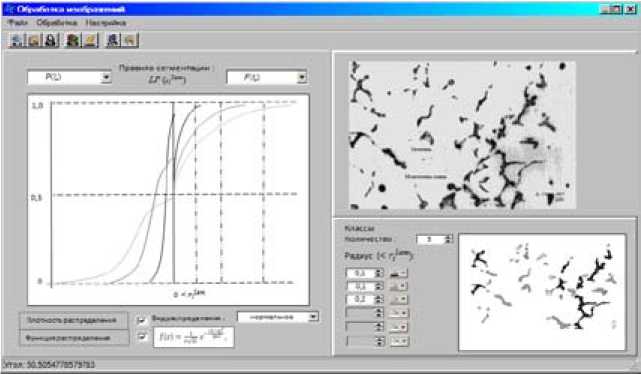
Рис. 2. Сегментированные области вблизи дефекта

Fig. 2. Segmented region close to the defect

Так, комбинированное правило сегментации имеет следующий вид:

1 5 , ( b 4² ): P (У - LP ( S iSem ) I < r ^Sm ,                                                        (3)

где r i^Sem – радиус свойства объекта типа «микротрещина».

Оценка r iSem может быть изменена в процессе сегментации за счет анализа ^ _г и относительно оценки однородности смежных классов.

Заключение

Предлагается математическая постановка задачи сегментации, учитывающая относительно более сложную модель соседства, выраженную функцией P ( ^ _г), характеризующей свойства объекта при отображении на матрице изображения:

Пусть задано s i (b i ² ) - множество отношений соседства компонент плоскости изображения (модели), признаки которых отображены некоторой функцией P (У, а также предикат LP ( s iSem ), определяющий радиус однородности r ^Sem .

Для детерминированной модели решением задачи сегментации является разбиение s i на N классов, для которых LP ( s i^Sem ) принимает истинные значения, удовлетворяющие цели.

В этом случае сегментацию можно рассматривать как комбинированную стратегию

Seg: V f(а ) -—— n ^{( Sem} ■) , где n i ^{( Sem .)} е N - семантическое отношение (имя объекта), определенное при анализе однородности границы области.

Предполагается, что синтаксис правила (3) будет дополнен оценкой компактности области и геометрическими измерениями на основе наложения диаграмм Г.Ф. Вороного и Б.Н. Делоне на изображение. Это не только позволит сегментировать область изображения с целевыми свойствами (рис. 2, области выделенные темным тоном), но и анализировать влияние контекста (рис. 2, области, выделенные относительно светлым тоном).

Разработка стратегии сегментации даст возможность:

• 1)    снизить влияние ошибок, возникающих в результате применения правила, характерного для традиционной сегментации;

• 2)    ориентировать смысл задачи сегментации на анализ признаков части изображения, представляющей свойства объекта;

• 3)    использовать механизм обратной связи для формирования правила комбинированной сегментации;

• 4)    применить диаграммы Г.Ф. Вороного и Б.Н. Делоне для оценки взаимного влияния классов объектов;

;

• 5)    использовать возможности алгоритмов интеллектуального поиска для выработки и оптимизации правила сегментации.