Стратифицированное течение двухслойной смазки в зазоре упорного подшипника, обладающего повышенной несущей способностью

Введение. Известно, что с помощью экспериментальных методик получена необходимая информация о межмолекулярном взаимодействии на границе раздела жидкости с твердым телом, в результате которого происходит образование структурированных пристенных слоев жидкости с иными (чем в объеме) свойствами [1-3].

Очевидно, что при наличии в смазочной жидкости подшипника скольжения частиц присадок или продуктов износа и окисления, а также за счет пристенной ориентации ее молекул происходит разделение смазки на слои с различной вязкостью. Известные решения [4,5] задач о стратифицированном течении вязкой несжимаемой жидкости в кольцевом пространстве, а также задач [6,7] о спектре фазовых скоростей внутренних волн в слабостратифицированной двухслойной жидкости и о внутренних волнах с турбулентной струей в стратифицированной жидкости не отражают специфику стратифицированного течения двухслойной жидкости в зазоре упорного подшипника, обладающего повышенной несущей способностью.

Цель работы – разработать аналитический метод расчета упорного подшипника с адаптированным профилем его опорной поверхности, обеспечивающей повышенную несущую способность подшипника, работающего на стратифицированной двухслойной смазке. Оценить влияние вязкостного отношения слоев и параметра, характеризующего адаптированный профиль опорной поверхности подшипника, а также параметра, характеризующего границу раздела слоев на основные рабочие характеристики подшипника.

Постановка задачи. Рассматривается установившееся стратифицированное течение двухслойной вязкой несжимаемой жидкости в зазоре упорного подшипника скольжения с адаптированным профилем опорной поверхности (рис.1). Предполагается, что ползун неподвижен, а шип движется в сторону сужения зазора с заданной скоростью u ^*.

Рис. 1. Схематическое изображение двухслойной смазки в зазоре упорного подшипника

В декартовой системе координат x' O' у' уравнения адаптированного контура ползуна С П , границы раздела С Г , а также направляющей С Н можно записать в виде:

у ' = h ₀ + x'tgа - a' sin о'x'- h '( x '); у ' = a h '( x '); у ' = 0.                         (1)

Здесь a e [0,1] , h ₀ - начальный зазор; tg a - угловой коэффициент линейного контура; a' и О - соответственно амплитуда и частота контурных возмущений, характеризующих степень отклонения контура ползуна от прямолинейного. Предполагается, что ltgа и a' одного порядка малости; о = Оl в дальнейшем определяется из условия максимума несущей способности подшипника ; l - длина ползуна.

Точное схематическое изображение контуров C n и С _Г можно привести после определения оптимального значения (по несущей способности) параметра ω , характеризующего адаптированный нелинейный контур ползуна.

Основные уравнения и граничные условия. В качестве основных уравнений берется безразмерная система уравнений движения вязкой несжимаемой жидкости для случая «тонкого слоя» и уравнение неразрывности:

д 2ип dp   ди   ди

? = ^p , — + — = 0, ( i = 1,2),                     (2)

ду2   dx   ду   дx где размерные величины x', у',и', u', p' в смазочном слое связаны с безразмерными x, у,и,, u, pi соотношениями:

h          *       * l Hi ^u

.

у = h0 у; x = I *x; V, = u V,; u, = u eu,, e = —, p, = яд, p, = —— l                            h0

Здесь ui',u' - компоненты вектора скорости; p/ - гидродинамическое давление в смазочных слоях; н, - динамический коэффициент вязкости.

Граничные условия на поверхности ползуна и направляющей записываем в виде:

p * h

U 1 у = 0 = 0; U , = 1; p , (0) = p , (1) = ^p      = P g ;

¹                                      l у u

u 2 | r = h ( x ) = ⁰ ; ^U2 | r = h ( x ) = ⁰ ; p 2 ⁽⁰⁾ = p 2 ⁽¹⁾ =

p a^h 0

l h₂ u *

= P g .

На границе раздела слоев:

1 | у = a h      2 | у = a h       1 у = a h

= I ■ ди, I

^U 2 | у = ^{a h ;} д у I у = ^{a h}

u , « X W X               ■            ltga

— = a h ( x ); h ( x ) = 1 + n x - n , sinrn x ; n =---- ;

^U1                                                         ^h 0

= 1У 5U 2 I .

у = a h ^;

H 1 ^д у ¹

a'

• n, = —; ю = ю l .

• ¹     h 0

Граничные условия (5) означают прилипание смазки к поверхности ползуна и направляющей. Условия (6) означают: равенство скоростей, касательных и нормальных напряжений на границе раздела слоев, а также условие существования слоистого течения смазки, т.е. требуется, чтобы скорость точек границы раздела слоев в каждой точке была направлена по касательной к контуру раздела слоев.

Точное автомодельное решение системы уравнений (2), удовлетворяющее граничным условиям (5) и (6) с учетом (7), ищется в виде:

д у,                 д ^

u , = — ¹ U , ^{( x} , у ); и = — + V ^{( x} , у ); у, = у , ©;

д x                     д у               '

r

U i ⁽ x , y ) ^{- —} u i ^(E) h ⁽ x ); V ⁽ x , y ) = ^U i ^(E) ; ^E = 7;

h

dp1   c1    c2 dp2   c1

dx   h2   h3 ; dx    h2

Подставляя (8) в (2) и в граничные условия (5) и (6) с учетом (7), будем иметь:

~    ~~

V ] - с ₂; U j - с 1 ; u 1 + EU 1 - 0; v₂ - ^c ₂; u₂ - c 1 ; u ₂ + Eu₂ - 0 v 2 (0) - 0, uu (0) - 0, U 1 (0) - 1, V 2 (1) - 0, u ₂(1) - 0,

U 2 (1) - 0,

V ] (a) = v 2 (a), U 1 (a) = U 2 (a), U , (a) - U ₂(a),

U ^] (a) = — U 2 (a), μ₁

α

^”^(a) = w 2'^(a) , Р 1 ^{- Р} 2 p 2 , J ^U1^(E) + f ^U2^(E) d ^{E -} 0. μ₁                   μ_{1       0 α}

Учитывая, что расслоение смазки на слои происходит вблизи неподвижной твердой поверхности, т.е. при значениях а , близких к единице, условие раздельного течения смазки ( й i (a)/U i (a) ) - a h ' (9) в принятом нами приближении удовлетворяется. На самом деле из граничного условия

U₂ (a) + aU 2 (a) + J U 2 ( E ) d E - 0

α следует

U 2(a)

u ~2 ( a ) + _a + 1 U 2 (E) d E

= 0 .

^U2^(a)        a ^u 2 ^(a)

Используя теорему о среднем значении, будем иметь

U 2(a)

u₂ (a)       U₂ (a * )

( 1 — a ) , a * e (a,1).

Так как    U₂(a * ) < U₂(a), (1 — a) << 1, следовательно, с точностью до членов

^-^ ( 1 — a ) ! будем иметь:

( ^U2^(a)         )

α

J U 1 (E) d E * 0, J U 2 (E) d E * 0.

α

Решение задачи (9) – (10) находим непосредственным интегрированием. В результате будем иметь:

V

~ f ψ₂

ξ ²

^— с ^ 2 ""2"" ⁺ с 2 ^{E +} с 3 ,

- E2

^— с ^- 2 ""2"" ⁺ с 4 ^{E +} с 5 ,

^U1 ^- с1^ ⁺ с 6^{E +} с 7^;

U 1 -

—I

ξ³ c

—

ξ2

c 6 2 ^{+ c} i0 ;

p 1 - C 1 J ₂ ( x ) + c₂ J 3 ( x ) + c ₁₂;

x

~

~

^U2 ^— с- 1 ""2"" ⁺ с 8^{E +} с 9 ;

-

u 2 -

ξ3

— c

—

ξ2

c 8 2 ^{+ c}11 ;

-

J к(x) - Jл           . v о (1 + nx — П sm ®x)

p 2 - c 1 J 2 ( x ) + c₂ J 3 ( x ) + c 13 ; dx

k .

Для определения постоянных c i ( i — 2,3,...13) и

~   ~   ~   ~ c1, c2, с1, с2 придем к следующей алгеб-

раической системе из 16 уравнений с 16 неизвестными:

— с7 — 1;  с10 — 0;  с3 — 0;  с12 — рg ;  с13 — рg ;

—

^{— с}1

3 ^— c 8 2 + ^с 11 = °;

- 1

с. — + с„

12     8

—

+ с 9 — 0; с- 2 — + с 4 + с 5 — 0

μ с1 = — с1;

μ1

μ2

' 2 ^—      с 2 ;

с 1 J 2 (1) -----;

J 3 (1)

μμ с, а + с, — — с, а + с„ ; с а + с — — с а + с. ;

16  1822  24

μ1                               μ1

2                             2

~ а             - а с 2--+ с 2 а + с3 — с 2--с4 а

α3 α2

с, — + с, — + с ₇ а — с,

1 6       6 2       7       1

~ ~ а

— с- — 0; с + с г а + с₇ — с

5    12671

а3   а2

"6 - с 8 “2" - с 9^{а + с} 1 ^ ⁺ с 8 2 ⁺ с 9

с ₈а — с 9 — 0;

— 0.

Решение системы (12) сводится к решению следующего матричного уравнения

—

M • x — b ,                                         (13)

где x — { 5; c 4 ; c 5 ; c 8 ; c 9 } ; b — { 0;0; — 6а;0; — 2 }

	— J 2 (1) J 3 (1)	2		2	0	0
	1	0		0	2	2
М —	k а — а + 1	0		0	3 k а2 — 3 a 2 + 3	6 — 6а
	(1 — k )а2 J 2^ 1 ) J 3 (1)	2а( k — 1)		— 2	0	0
	а2( k — 1)	0		0	2а( k — 1)	— 2
Решая матричное уравнение (13), получаем
^    6 + 6 к а2		— 6а2	J 2 (1) J 3 (1)	3 —	6а2 + 3а4 + 3 k2 а4	— 6 k а4 )
с 1           A		;    с 4 —			( а k — а + 1 ) A	;

— J ² 0) а f— 3а² — 3а + 3а³ + 3 + 6 k а² — 3 k + 3а³ k² — 3а² k² — 6 ka ³ + 3ak —

J 3 (1) ⁽ ________________________________________________________________________________

( а k — а + 1 ) A

— 3а k в — 3а² k ² — 6 k а³ + 3а k )

4 — ва² — 4а³ + 4 k а³          — 4а³ + 4 k а³ — 3 k а² + 3а² + 1

с 8—------------;------------; с9—-----------------;;

AA c 2   kc4 , c6

A — — 4а³ + 1 + а⁴ — 6 kа² + 4 k а³ + k ² а⁴ + 4 k а — 2 k а⁴ — 4а + 6а²;

J2 (1)    ,    1       П1 /                               [,    1П1 /

—— — 1 + — п + — ( cos ю — 1 ) ; с₂ — — с₁ 1 1 + — п + — ( cos ю —

J3 (1)      2    ю                     ^   2ю

~     1 ~     ~        ~   1 .         ./

с, — kc, , c — — c  I +   n + П1 ( cos ® —

1    12    1    2

Перейдем к определению основных рабочих характеристик подшипника.

Безразмерные расходы Q ₁ и Q ₂ двухслойной смазочной жидкости определяются выражениями:

α3      α2                c2   c4           α3α

Q — c + c + c a ;    с Л —-- 1--- + c^ — c_R--c     — c - a.

1     26      22     3         2    6     2     5     66     42

С использованием формул (12) и (14) для безразмерного гидродинамического давления p1 , безразмерной поддерживающей силы Ry и безразмерного момента трения Lтр , получим вы- ражения:

P 1 ^{— c} 1

1       1 ηη

— n x n x + — ( cos® x — 1)—— (cos® —

22ωω

~

R y

R y    ¹

— — I P 1 ( x ) dx — c p ₁ ^* l    ₀

П n₁ n₁sinm n₁ ( cos® — 1 )

12 ⁺ 7 ^— .    ⁺     2®

;

c 2

L тр

L тр l

* μ u

1^ + u(0)

I h ^!( x )     h ( x )

к              7

2n. ,             .           . n П. /

1 — n--(cos ® — 1) + c^ 1----(cos ® —

¹    ® ⁽            )       6        2 to ⁽

Прежде чем привести результаты численного анализа, отметим, что предлагаемая модель имеет смысл, если область 0 <  ^ <  1 охвачена вязким течением.

Результаты численного анализа полученных аналитических выражений (16) для основных

рабочих характеристик, показывают:

• 1)    такой реально существующий фактор, как сложная двухслойная структура смазочной жидкости, приводит к изучению влияния структурного параметра α и вязкостного отношения k на основные рабочие характеристики подшипника, прежде всего, на поддерживающую силу;

• 2)    как и ожидалось, при α =0, α =1 имеет место единый смазочный слой. В первом случае зазор заполняется более вязкой жидкостью, во втором случае менее вязкой. В первом случае несущая способность значительно выше. Граница раздела, определяемая параметром а , зависит от расхода Q=Q 1 +Q 2 и вязкостного отношения k = µ 2 / µ 1 ;

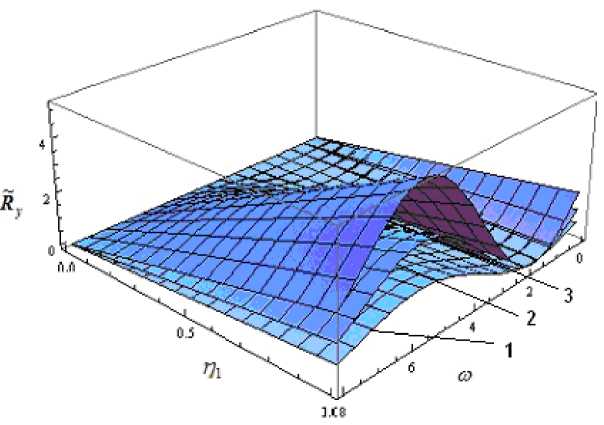
Рис.2. Зависимость безразмерной несущей способности от конструктивного параметра η = η 1 и от параметра ω , характеризующего адаптированный нелинейный контур опорной поверхности подшипника

1 — к — 1; 2 — к — 1,5; 3 — к — 4

• 3)    при значении ω ≈ 4 несущая способность подшипника при любом значении α ∈ [0,1] практически в два раза выше, чем при ω =0 (рис.2);

• 4)    с увеличением значения вязкостного отношения k несущая способность подшипника резко возрастает при значениях α ∈ [0,95-0,99].

Выводы. Предложено точное автомодельное решение задачи о стратифицированном течении смазки в зазоре радиального подшипника с адаптированным профилем опорной поверхности. Теоретически обоснован профиль, обеспечивающей повышенную несущую способность подшипника.