Стратифицированное течение трёхслойной смазки в зазоре упругодеформируемого упорного подшипника, обладающего повышенной несущей способностью

Введение. Как известно, работа машин и их долговечность в значительной степени зависят от конструкции и качества подшипниковых узлов. Улучшение работы узлов трения может быть достигнуто совершенствованием методов расчёта подшипниковых узлов и их конструкций. В новых машинах и механизмах, как правило, проектируется рост скоростей вращающихся узлов, увеличение статических и ударных нагрузок, действующих на опоры скольжения. Задачей современной инженерной практики является повышение требований, предъявляемых к подшипникам скольжения. Это, прежде всего, обеспечение надёжной работы подшипников скольжения [1‒5]. Указанное требование выполняется при использовании упругих и податливых подшипников. В настоящее время возрос интерес к применению в узлах трения машин и механизмов упругодеформиру-емых подшипников, поскольку они обеспечивают большую устойчивость в работе, чем соответствующие жёсткие подшипники. Анализ существующих работ, посвящённых расчёту упругоде-формируемых подшипников показывает, что в существующих расчётных моделях упорных подшипников не учитываются особенности взаимодействия смазочной жидкости с твёрдой опорной поверхностью как ползуна, так и направляющей. Профиль опорной поверхности упорного подшипника считается традиционным (линейным) и не обеспечивает его повышённую несущую способность. В известных работах [6‒10], посвящённых стратифицированному течению ньютоновской смазки в зазоре упорного подшипника, его опорная поверхность считается абсолютно жёсткой. Таким образом, задача связанная с разработкой расчётной модели упругодеформируемых упорных подшипников, работающих на трёхслойной смазке, обладающих повышенной несущей способностью остаётся нерешённой. Решение этой задачи является основной целью данной работы. Постановка задачи. Рассматривается установившееся стратифицированное течение трёхслойной вязкой несжимаемой жидкости в зазоре упорного подшипника скольжения с адаптированным

Работа выполнена в рамках программы НИР.

профилем опорной поверхности. Предполагается, что ползун неподвижен, а шип движется в сторону сужения зазора с заданной скоростью и* (рис. 1).

Рис. 1. Схематическое изображение трёхслойной смазочной композиции в зазоре упорного подшипника:

1 — контур жёсткой опорной поверхности ползуна; 2 — упругий слой ползуна; 3 — недеформированный контур ползуна;

4 — деформированный контур ползуна; 5 и 6 — границы раздела слоёв; 7 — направляющая

В декартовой системе координат xOy (рис. 1) уравнение деформированного контура ползуна (поз. 4), недеформированного адаптированного контура ползуна (поз. 3), границы раздела слоёв (поз. 5 и 6), а также направляющей (поз. 7) можно записать в виде y' = h0 + X tg а* - a sin ы'x' + Л'ф (x') = h (x'), y = h0 + Xtga*-asinы'x' = h'(X), y = eh'(X), y = ah'(X), y' = 0.

Здесь a e [ 0,1 ] , h₀ — начальный зазор до деформации; tga * — угловой коэффициент линейного контура; а' и ы ' соответственно амплитуда и частота контурных возмущений, характеризующих степень отклонения контура ползуна от прямолинейного, Л ' ф ( X ) — ограниченная функция (при x e [ 0, l ] ), подлежащая определению.

Предполагается, что l tga * и а одного порядка малости, ы = ы ' l в дальнейшем определяется из условия максимума несущей способности подшипника, l — длина ползуна.

Точное схематическое изображение контуров (рис. 1, поз. 3, 4, 5, 6) можно привести после определения оптимального значения (по несущей способности) параметра ω, характеризующего адаптированный нелинейный контур ползуна. Уравнение недеформированного контура, прилегающего к жёсткой опорной поверхности задается в виде y = h 1 + X tga * .

Основные уравнения и граничные условия. В качестве основных уравнений берётся безразмерная система уравнений движения вязкой несжимаемой жидкости для случая «тонкого слоя» и уравнение неразрывности

= dp i- , d U i ■     = 0, ( i = 1,2,3)

d y2   dx   Sy где размерные величины x', y', u', u,, pi в смазочном слое связаны с безразмерными x, y, υi , ui , pi следующими соотношениями y = /0y, X = l ■ x, и'= u*u,, и', = Уги,, е = h0, p', = pip,, pi = l^iu-.(3)

lh

Здесь u i , и ' — компоненты вектора скорости, p i — гидродинамическое давление в смазочных слоях, μ _i — динамический коэффициент вязкости.

Граничные условия на поверхности ползуна и направляющей записываются в виде:

u i У =0 = ⁰ , ^U1 = 1, P l ( ⁰ ) = P l ( 1 ) =

P a- h L

/ M i u'

= P gi , P l ( 0 ) = P l ( 1 ) =

p а h 0 ²

l μ₂ u

*

~

= P g 2 ,

u 3 | r = h ( x ) = ⁰ , ^U3 | r = h ( x ) = ⁰ ,   ^P 3 ^{( 0} ) = ^P 3 ^{( 1 )} =

p а h 0 ²

/ Ml u'

~

= P g 3^.

На границе раздела слоёв:

u i I у =a h = u 2 I у =a h , ^U1 | у =a h = ^U 2 | у =a h , д у

у =a h

= Ml d U L

M 1 d у

u ¹ = a h '( x ) , h ( x ) = 1 + n x - nsinto x + п₂Ф ( x ) , n = l tg^a υ₁                                        1             2                   h ₀

, у=a h a'

^П2 = h '   ^{ф (} x ) = ^{ф (} lx ) , u 2 | r =в h = u 3 | r =в h , ^U2 | r =e h = ^U3 | r =e h , ^ r

, П 1 = T'

1    h ₀

= M s. d U i

r = ^{e h}   M₂ d r

to = to ' / ,

r = eh ,

Граничные условия (4) означают прилипание смазки к поверхности ползуна и

u ² = ₽ h '( 0 ) .

υ2

направляющей.

Условия (5) означают равенство скоростей, касательных и нормальных напряжений на границе раздела слоёв, а также условие существования слоистого течения смазки. Требуется, чтобы скорость на границе раздела слоёв в каждой точке была направлена по касательной.

К системе уравнений (2) необходимо добавить безразмерные уравнения Ламе для случая «тонкого слоя»

d ² u..,         L^u ,

---У- = 0, 1 ^ x 2- = 0. d у     ay

В упругом слое переход к безразмерным переменным осуществлён по формулам

У' = (h1 - h0) У, x' = /x, uy, = й^у,, ux, = U*ux, где uy,, u'x, — компоненты вектора перемещений; u* — характерная величина компонента вектора перемещений.

С учётом (7) безразмерные уравнения контуров (рис. 1, поз. 1 и 3) в переменных у* и х, запишутся в виде

~

У*

= h ⁰ + П 3 x - ^sinto x = h i ( x ) , y* = h + П 4 x = h 2 ( x ) , δ₁

δ

= ^h 1 ^{- h} 0^.

duv,

M ^У д У

у * = h ( x )

-     duy.

- P , N—x- д у ‘

d u ₂

д у

У = h 1 ( ^x )       ’

,

У = h ( x )

^UУ 'I у * = h 2 ( x ) = ⁰ , ux' У * = h L ( x ) = ⁰ , ^{h ( x} ) = ¹ + ^{n x} - ⁿ1 s ^{into x} ,

M Gu *h „ G (1 - a) u *h r где N =----2, M = —---°, G m2u*61         (1 - a) u*m261

—

— модуль сдвига; α

—

постоянная Мусхелишвили;

p = max p , x e [ 0,1 ] ; р — безразмерное гидродинамическое давление.

Граничные условия (9) означают: равенство касательных и нормальных напряжений на недеформированной адаптированной опорной поверхности; равенство нулю компонентов вектора 78

перемещений на границе упругой поверхности, прилегающей к жёсткой опорной поверхности ползуна.

Точное автомодельное решение задачи. Точное автомодельное решение системы уравнений (2), удовлетворяющее граничным условиям (4)‒(5) ищется в виде ui = -dy + Ui (x, y), ui = ^ + Vi (x,y), ф, = фi (5), i

Ui (x,y) = -Ui (5)h (x), Vi (x,y) = Vi (5), 5 = yh, dp1   c1   c2   dp2   c1   c2   dp3   c3

I ,                                                        I , dx  h2  h3   dx  h2  h3   dx   h2

Подставляя (10) в (2) и в граничные условия (4) и (5), будем иметь

Ф 1 = c 2 , u 1 = C 1 , U 1 + 5u ; = 0, ф 2 c 2 , U 2 = q, u 2 + 5u2 = 0, ф 3 c 4 , u 3 = c 3 ,

U 3 + 5U 3 = 0, ф ; ( 0 ) = 0; U 1 ( 0 ) = 0, U 1 ( 0 ) = 1, Ф 3 ( 1 ) = 0, U 3 ( 1 ) = 0, U 3 ( 1 ) = 0,

ф ; ( a ) = Ф 2 ( a ) , U 1 ( a ) = U 2 ( a ) , U ( a ) = U 2 ( a ) ,U₂ ( в ) = U ( в ) , U 2 ( в ) = U 3 ( в ) , Ф/ ( в ) = ф 3 ( в ) , ⁽¹¹⁾

U ; ( a ) = yU 2 ( a ) , Ф 1 ( a ) = N; ( a ) , Р 1 = H 2 P 2 , ф 2 ( в ) = ф 3 ( в ) £, U 2 =       ( в ) , Р 2 = ^ Р з ,

μ1                      μ1                  μ1                          μ2          μ2μ

Ju; (5) d 5 + JU2 (5) d 5+J U3 (5) d 5 = 0.(12)

0αβ

Решение задачи (11)‒(12) находится непосредственным интегрированием. В результате будем иметь

ξ2                            ξ2ξ ф1 (5) = c2 у + c25 + c3, ф2 (5) = c2 у + c45 + c5, U1 (5) = cry + c65 + С7,

ξ2                             ξ3ξ

ξ3      ξ2

^U 2 ( ⁵ ) = " ^c 1y — c 8 У ⁺ c H,

U2 (5) = c1y + c85 + c9, U1 (5) = "c1y — c6 У +

2          232

ф3 ( 5 ) = c4^ + c^ + c„, U3 (5 ) = c3L + c„5 + c„, U3 ( 5 ) = -c3^ - c„y + c16,(13)

Р1 = c1 J2 ( x ) + c 2 J3 ( x ) + c17, Р2 = c1 J2 ( x ) + c 2 J3 ( x ) +

Р 3 = c 3 J 2 ( x ) + c 4 J 3 ( x ) + c 19 ,

x dx

J k ⁽ x ) = ^J h^k ( x ) "

Для определения постоянных ci (i = 2,3, .„ ,19) с1, с2, с1, с2, c3 и c4, придём гебраической системе из 24 уравнений с 24 неизвестными cc c7 = 1, c10 = 0, c3 = 0, c17 = pg1, c18 = pg 2, c19 = pg 3, c13 =   у - c12, c15 =   5" - c14,

к следующей ал-

c 16

c 3    c 14

+      ,

c6 = k1 (ca + c8) - c1a, c. = ^2 (c.в + c12) - cгв, c2 = k1c., c8 = k2cM, a               a

• ^c ₂ у ^{+ c} 2^{a + c} ₃ ^{- c} 2 у ^{- c} 4^{a - c} 5 = ⁰ , ^c 1

^ в3 в2         - в3в

• ^{- c} 1 у ^{- c} 8 у ^{+ c} 11 ^{+ c} 3 у ^{+ c} 14 у ^{- c} 16 = 0,

α2α у + c6a + c7 - c1 у - c8a - c9 = 0, г в2-в c2 у + c4в + c5 - c4 у - C12в - c13 = 0,

β2                  β2

c 1 у + c 8 в + c 9 - c 3 у - C 1 ₄в - c 15 = 0, c 1 = k 1 c 1 , c 2

= k 1 c 2 , c 1 = k 2 c 3 ,

c ₂

= ^k2 c 4 ,

c 4 = ^{- c} 3

^J 2 ( 1 )

^J 3 ( 1 ) ,

α3      α2            β3      β2

c 1- 6 ^{+ c} 6y ^{+ c} 7^{a + c} 1y ^{+ c} 8y ^{+ c} 9

β

α3

-

c 1 6

α2

-

c

„  c ₃    c ₁₄   „    - в³   _  в²   _ О П

- c a +---1---+ c e - c₃--c₁₄--c t-в = 0.

9      6     2      15    3 6      14 2      15

Здесь k = —, k = 2 3 .

1 μ₁      2 μ₂

Решение системы (14) сводится к решению следующего матричного уравнения

M l ■ x = b,                                            (15)

где x = {c3; c4; c5; c6; c9; c11; c12; c14}, b ={0;0;0; -1; 0; 0; 0; - 6a} 0 1 0 0 0 0 -k2 0 0 0 0 1 0 0 0 -k1k2 α1 α2 -1 0 0 0 0 0 M = α3 α4 0 0 0 0 α 0 -1 0 0 1 0 0 -k2a α5 .                              (16) α6 β 1 0 0 0 α7 0 α8 0 0 0 1 0 0 α9 α10 0 0 3α2 α11 0 0 α12 α2 Здесь 01 = k2 — J2 (1) J 3 (1)(1 k1);C 2 = 0 (k1- - 1) , 03 = k2α2 2 (k1 - 1) , a4 = 3(в3 -kв -1); a5 = 2(в2 -в2k2 -1); a6 = 2 J^^2 -k2e2 -1),

07 = 1 - в; a8 = 2 (1 - в2 + к2в2), a9 = 1 + вк - в, a10 = -2 - в3 + 3в - k2a3 + к2в3 + k1k2a3, 011 = 6 (в - a), a12 = 6в + 3 (1 - в2 - k2a2 + k^).

Решая матричное уравнение (15), получим:

С 1 = k 1 k₂c₃, c ₃ = - ( 3 k 1 k ₂a² + a₁₂ - 0 11 0 9 )/( 3a₃ k ₁ k ₂a² + a₃a₁₂ - 0 3 0 11 0 9 + 3 k ₂a₈ k 1 a² + a₁₀ k ₂a - kk a_ina + k a_Ra,. k .a - k₂ а^.а - aa_ina_q + a_Ra₁₂) + 6fa_q - akk )a/(3a₃ kk a² + a₃a,, -

1 2 10        2 8 11 1        2 8 11          10 9      8 12            9        1 2            3 1 2          3 12

• - 0 3 0 11 0 9 + 3 k ₂a₈ k 1 a² + a₁₀ k ₂a - k ₁ k ₂a₁₀a + k ₂a₈a₁₁a k ₁ - k ₂o₈o₁₁o - a₁₀a₁₀a₈a₁₂ ) .

• с ₂ = k 1 c 4 , c 4 = - k ₂ ( - 6a₁a k ₁ k ₂в - 6a₆a k ₁ k ₂в + 6a₁a² k ₁ k ₂ + 6a₁ k ₂aв + 6a₆a² k ₁ k ₂ + 6a₆ k ₂aв -- 3a 1 a₂² k 1 k ₂ - 3a₆a₂² k 1 k ₂ - 0 1 0 12 - 6а₁а₉в + 60 1 0 9 a - 6a 1 k ₂a² - 6а₆а₉в + 6a₆a₉a - 6a₆ k ₂a² +     (17)

+ ^a1^a11^a9 + ^a6^a11^a9 ^{- a}6^a12 )/( ( ^a7 + ^{в k} 2 + ^a2 ^k 2 ) ( ^3a8^{a 2 k} 1 ^k 2 ^{- 0}11⁰8 ^k 2⁰ + ⁰3⁰12 + ⁰10 ^k 2⁰ + ⁰8⁰12 + + 3a₃a 2 k 1 k ₂ - a₁₀a₉ - a₁₀a k 1 k₂ + a₁₁a₈ak₁k₂ - 0 3 0 11 0 9 ) ) ,

• c ₆ =- k 1 ■ k ₂ ( 0 11 0 8 - 6а₃в - a₁₀ + 6a₃a - 6а₈в + 6a₈a )/( a₁₀ k ₂a + 30₈a 2 k 1 k ₂ + 30₃a | k 1 k ₂ + + ^a11^a8^{a k} 1 ^k 2 ^{- a}3⁰11⁰9 + ⁰3⁰12 + ⁰8⁰12 ^{- 0}10⁰ k 1 ^k 2 ^{- 0}10⁰9 ^{- 0}11⁰8 ^k 2⁰ ) .

При определении основных рабочих характеристик подшипника выражения для остальных констант, входящих в систему уравнений (14), нам не понадобятся. Ввиду громоздкости выражений для этих констант здесь они не приводятся. Перейдём к определению основных рабочих характеристик подшипника. Для определения безразмерного гидродинамического давления р1 имеем следующее уравнение dP1 = c1   + c 2

dx   h ² ( x ) h ³ ( x ) .

Для интегрирования уравнения (18) предварительно необходимо найти функцию п2Ф (x). Инте- грируя первое уравнение системы (6), с учётом граничных условий (9), будем иметь uy ‘ =

—

~           ~ / I-\ p . p । h 1

y +       + n4 x.

My M (51

Воспользуемся приближённой формулой h ( x ) — h ( x )| * u_y ,| * ^ . Тогда для п ₂ Ф ( x ) с точностью до O I MM I , получим следующее приближённое выражение

П 2 Ф ^{( x} Ь M ■

Здесь p — безразмерное гидродинамическое давление, найденное в работе [6] при решении задачи о стратифицированном двухслойном течении смазки в зазоре упорного подшипника с жёсткой опорной поверхностью. Как видно из формулы (20) следует, что значение безразмерной функции п 1 Ф ( x ) (обусловленной деформацией опорной поверхности) прямо пропорционально безразмерному значению давления p и обратно пропорционально значению упругогидродинамического параметра M . При M > / , ф ( x ) ^ 0.

C учётом (20) уравнение (18) запишется в виде

*

где n

η

,

1 + p

M

dPi =____________<____________+ dx f P 1 /       .        .          \2 f P

I ^{1 +} M 1 ( 1 ⁺ n x ^— n * ^sin “ ^x )    I ^{1 +} M

n * =

η1

1 + p

M

c ₂

3 ,

I ( 1 + n * x — n * sinw x )

Оценку влияния гидродинамического давления недеформированного упругого слоя на опорной поверхности ползуна ниже приведём для её максимального значения. В уравнении (21) p заменим на p * = max p . Интегрируя (21) с точностью до членов O ( n * ² ) , O ( n 1* ² ) для безразмерного гидродинамического давления будем иметь

c

P = 7-- f1+P7

I M

т 1n * x 2

!² 2 ¹

—

n x ni /             1 \ ni /           ₁X

+ — ( costo x — 1 ) — ( costo — 1 ) x + p

2ω     ω

g

_г                       д J (1)

С учётом выражений для с ₂ и J ( 1 )

С P * 1 fl n * n * I 1

£ = — 1 + — с 1 + — + —(cos to — 1 ^{2       1} M I ¹ 1        2 to ⁽

—

*     _n *                  1

1 + —+ -!1 ( cos го — 1 ) ,

2 to ^v ’ I

для безразмерного расхода в каждом слое получим следующие выражения

α                 α3      α2                β                 β3 β2             α3α

Q 1 = J ip 1 ( ^ ) d 5 = C 2    + с 2     + с 3 a, Q 2 = f ip 2 ( ^ ) d s = C 2 j^ c 4     + с 5 в — с 2 5г — с 4     — с 5 а,

0         6    2        α         62       62

1                   1        1              β3β

^Q 3 = Р з ( ⁵ ) ^{d 5} = ^с 4Z ^{+ с} 12й ^{+ с} 13 ^{— с} 4    ^{— с} 12^ ^{— с} 13^в .

β      62     62

Безразмерная несущая способность R и безразмерная сила трения L _тр определяются выражениями

~

Ry

R ¹

=j( pl ( Х ) — p)g ) ^< = p1 l   0

n * n * n * sin to n * ( cos to — 1 ) 12 ⁺ to - — ⁺--.

~ c 1

~

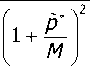
L тр

=        ' dx +

M 1^ ^J 0 h ² ( x ) h ( x )

, fl 2П1 2П11 L П n n dx ® c 1 - n--1 cos to + —1 + c 1 - - - — cos to + —

• ² ( to             to J ⁶ (     2 to to

5=0

Численный анализ полученных аналитических выражений для основных рабочих характеристик подшипника. Прежде чем привести результаты численного анализа, отметим, что предлагаемая модель имеет смысл, если вся область 0 < 5 < 1 охвачена вязким течением. Такой реально существующий фактор, как сложная трехслойная структура смазочной жидкости с необходимостью приводит к изучению влияния структурных параметров α и β (характеризующих границу раздела слоёв), вязкостных отношений k1 и k2 и упругогидродинамического параметра М на основные рабочие характеристики подшипника, прежде всего на поддерживающую силу. Как и ожидалось, при а = 0, в = 1 имеет место единый смазочный слой. При а = 0, в * 1, а * 0 имеет место двухслойная смазочная жидкость. В случае трёхслойной жидкости в * 1, а * 0, а < в.

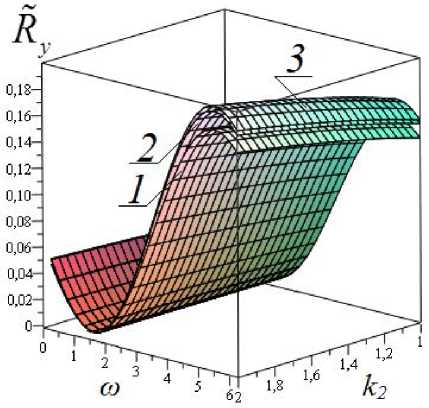
Рис. 2. Зависимость безразмерной несущей способности от параметров k 2 и ω при различных значениях упругогидродинамического параметра М:

1 — М = 100; 2 — М = 800; 3 — М = ∞, k 1 = 0,95

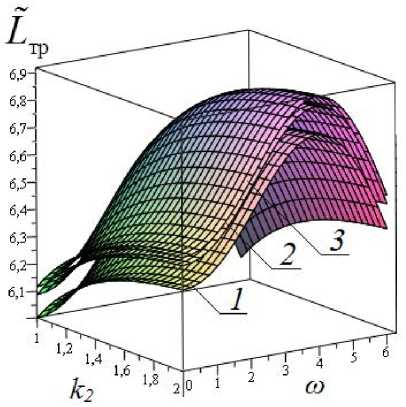
Рис. 3. Зависимость безразмерной силы трения от параметров k 2 и ω при различных значениях упругогидродинамического параметра М :

1 — М = 100; 2 — М = 800; 3 — М = ∞, k 1 = 0,95

Выводы. Результаты численного анализа, приведённые на рис. 2‒3, показывают.

• 1.    При а = 0, в = 1 (т. е. в случае единого смазочного слоя) наибольшая несущая способность достигается при to = 3п / 2.

• 2.    В случае трёхслойной смазки с увеличением значений вязкостного отношения k ₂ при к 1 ® 1, в, близких к единице и а, близких к нулю, несущая способность подшипника сочетается с наименьшим значением силы трения.

• 3.    Наиболее резкое увеличение несущей способности подшипника достигается при k ₂ >  3.

• 4.    С увеличением значения to сила трения возрастает. При to = 3п / 2 наблюдается экстремальное значение силы трения.

• 5.    При значении М ≤ 20 имеет место резкое уменьшение несущей способности подшипника.

• 6.    С увеличением значения упругогидродинамического параметра М значение несущей способности и силы трения возрастают, оставаясь меньше от соответствующих значений этих характеристик для подшипника с жёсткой опорной поверхностью. При М → ∞ значение несущей способности и силы трения стремятся к соответствующим значениям для подшипника с жёсткой опорной поверхностью.