Стратификация смазочного материала в радиальных подшипниках

Введение. Как известно [1-3], при наличии в смазочной жидкости частиц присадок или продуктов износа, а также за счет пристенной адсорбции и ориентации молекул, вблизи опорной поверхности подшипниковой втулки происходит стратификация смазочного материала на слои с различной вязкостью. Слоистое течение вязкой несжимаемой жидкости в зазоре упорного и радиального подшипников рассматривалось в работах [4-9]. Существенный недостаток существующих методик заключается в том, что в расчетной модели не учитывается зависимость вязкости от давления. При больших значениях давления в смазочном слое вязкость смазки существенно возрастает и возникает необходимость учета зависимости вязкости от давления.

Постановка задачи. Цель работы — разработать аналитический метод расчета радиальных подшипников, работающих на двухслойной смазке, с учетом зависимости ее вязкости от давления. Также необходимо оценить влияние вязкостного

отношения слоев; параметра, характеризующего границу раздела слоев на основные рабочие характеристики подшипника; параметра, обусловленного зависимостью вязкости от давления при осевой подаче смазки.

Задача № 1 . Рассматривается течение двухслойного смазочного материала в зазоре радиального подшипника бесконечной длины. Вал вращается с угловой скоростью Q, а подшипниковая втулка с адаптированным профилем опорной поверхности неподвижна. Зависимость вязкости от давления выражается формулой

Нг ⁼ Л О У ^Р .                                                (1.1)

В полярной системе координат с полюсом в центре вала (рис. 1.1) уравнения контуров вала, границы раздела слоев и адаптированного контура опорной поверхности запишутся в виде:

с₀ : г’ = r₀; q : А = 7'₀ + ба + ба cos 6 - аЛ sin со9:

q '.т — Tt"V ecos 0 — Л sin а>0, где а ее [0,1].                                      (1.2)

Здесь r 0 — радиус вала; r 2 — радиус подшипника; r 0+ ба — радиус границы раздела слоев; параметры Лию характеризуют адаптированный профиль опорной поверхности.

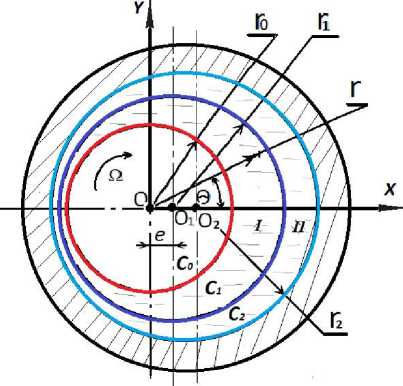
Рис. 1.1. Схема радиального подшипника с двухслойной стратификацией жидкого смазочного материала

Исходные уравнения и граничные условия . В качестве системы исходных уравнений берется безразмерное уравнение движения вязкой несжимаемой жидкости с учетом зависимости вязкости от давления и уравнение неразрывности

6²и.        . dp ди би.

—^ = е-^и1*Л^, -^ + ^ = 0 (/ = 1,2),

(1.3)

Dr~         dQ Dr 59

где размерные величины г’, Ц, и', р', ц'- связаны с безразмерными г, щ, и_;. р, ц, следующими соотношениями: г' = 7Ь+87^-, и';=Ог₀и_;, 1^=061^, р' = p_gp, ц'=ц_ОгЦг, 8 = ,'₂—/;_:),                      (1.4)

где а—экспериментальная постоянная; ц 0 i — характерные вязкости смазочных слоев; и^ ^, и' — компоненты вектора скорости; Q — угловая скорость вращения вала; р_е — характерное давление.

Система уравнений (1.3) решается при следующих граничных условиях:

»i1 г=0 = 0, q | r=0 = 1, р(0) = р(2л) = 1, z z21 Г=№) = 0’ и21 Г=№) = ^ “11 г uh =' z21 r=ah т и11 г uh = и21 г uh т

би,

_ Ц₀₂ би₂ I ц₀1 9г

-аЛ?

^|г=а/1=а//(9). о,

h (е)1+лcos 9 — т] ₁ sinго9, Л = e /б, Л1 A /б.

(1.5)

Точное автомодельное решение. Точное автомодельное решение системы уравнений (1.3), удовлетворяющее граничным условиям (1.5), будем искать, используя функцию тока, предполагая, что поле скоростей и давлений в сма

зочном слое является потенциальным и,=—^ + Ц(7-,9), и, =^ + ^(7-,9), щг=щг@.

и,(г,9) = -W). ^(г,9) = ц©- ^ = 7777

/?(6)

Л₂ dp^     с, с->

Д х Д   _____ 1   ।   Д

Др dQ “ /г2 (9) й3(9)’ где

Во? ~    ~    ц02 ~

М-01                М-01

Л, dp_x _ q 7₂ е^ dd - h² (9) ⁺ /г³ (9)

(1.6)

Осуществляя подстановку (1.6) в (1.3) и (1.5), получим:

(1.7)

Vr=c₂, 4' = q, ^+^=0, ^=с₂, u₂=q, i7₂+^u₂=0, Ф1(0) = 0; /7^0) = 0, иДО©!, щ'₂(1) = 0, z7₂(l) = 0, и₂(1) = 0, ф1(а) = ф₂(а), и₁(а) = и₂(а), z7₁(oc) = z7₂(a).

и^(а) = —и2(а), ф^(а) = -^щ^(а), [/)]© + [и2(^ = 0.

(1.8)

^             ^ о i

Решение задачи (1.7)—(1.8) находится с помощью непосредственного интегрирования. В результате получим

71 =С2у + С2§ + С3,

ф2 = 7,

?3

?2

— + с

„ 7

'4т> "Г с5 >

3 и 2     1 2

1 2

1 2

-7^

1 3

?2

Л1е“7'= Л,е“-a

a[q72(9) + c273(9)],

W^Hp = Л₂е“-a[7]J₂(9)

________те________

(1.9)

Для определения постоянных q(z=2,3, ...,11)71,72,71272 используется следующая алгебраическая система

из 14 уравнений с 14 неизвестными:

^С1 -1’ ^сю - 4 с₃ - 0,

~ 1    1       л ~ 1          л ~ 1          л

__ f~>__Д' 1_ д' —         д' 1_ д' _1_ д' — II       Д' 1_ Д' Д' -- I I

— Ci    Со  т Ci 1 —    Ci Со т Со — и.  С7  т С4 т С5 —

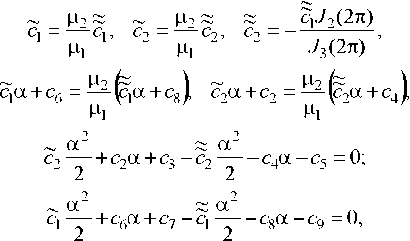
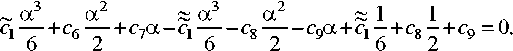
С учетом (1.4) гидродинамическое давление р определяется следующим выражением р = 1+ 1ч— — psin9 или р=1+ 1 + — ——nsin9.

(1.10)

(1.11)

Записывая систему (1.10) в матричной форме, получим:

М ■ х = Ь,

(1.12)

где x = p!; с4; с5; с8; сД 6 = {0,0, - ба; 0; - 2{,

	J^lK) У3(2л) 1	2      2 0      0	0 2	0 2
м =	ко? - а5 +1	0      0	Зка2 - За2 + 3	6-ба
		2а(/с-1) -2	0	0
	J3(1k)
	а2(к-1)	0      0	1а(к - 1)	-2

Решая систему (1.12), получим

Д(2л)                 1 4 о* 4 4ч б + бка2 - ба2

I 4 VzLA и LA I JLA LA Lz I LA Lz/LLA ) т /гу x X                   I                           I                                 "

J3(2k)

(ak - а + 1)A

^²^^Л^а(-За² - За + За⁵ + 3 + бка? - Зк + За³ к² - За² к² - бка³ + ЗаА')

Д(2л)

"                              (ак - а + 1)А

4 - 4а5 + 4Аа' - 4а5 + 4Аа' - Зка2 + За2 +1       ,,

г* — _______________________ Г1 — ______________________________________________ Г1 -          Г1 — 1Z г-

С8 —                , Lg —                                , С2 — ЛС4, L6 — ACg,

АА

А = -4а5 +1 + а4 - бка?" + 4А'а5 + к2а? + 4А’а - 2А’а4 - 4а + ба2, ^^- = 1 + -^-(со$2лсо-1), с. = -с/1 + -^-(со52лоэ-1)1 /3(2л) 2лю               "    \ 2лсо/

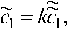
Д(2л)

2     1 73(2л)

(1.13)

Основные рабочие характеристики подшипника. Нормализованные показатели расходов Q1 и Q2 двухслойной смазочной жидкости определяются выражениями

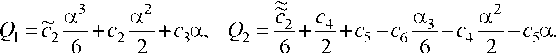
(1.14)

Используя формулы (1.13) и (1.14) для компонент нормализованной поддерживающей силы и нормализован -:

ro^

ар „ _ с, ту, —cos9d9 = — лтн—^L

49 А, 2ю

cos(co - 1)2л -1 cos(g) + 1)2л -1 co +1             co+1

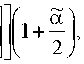
2тт                                г .

R_x rip . „ „ qr], sm(co-l)2n

J 29           A,2со го-1

^r8 0 Q           IL

sin(co + 1)2л CD +1

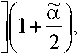
~ _ Др8 ^тр — з PiO^o

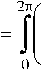
Ф1 й²(9)

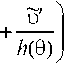
e^dd.

?=o

(1.15)

Итоги численного анализа полученных аналитических выражений для базовых эксплуатационных характеристик узла трения показывают следующее:

• -    при значении вязкостного параметра а е [0,1] несущая способность достигает максимума при величине параметра контура профиля cd = 16;

• -    с увеличением вязкостного параметра а несущая способность подшипника возрастает на 5-10 %.

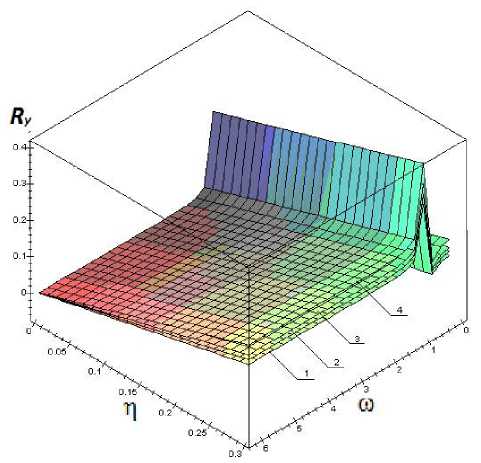
Рис. 1.2. Зависимость вертикальной компоненты безразмерной несущей способности Ry от параметра эксцентриситета ц и параметра адаптивного профиля со: 1 - а = ОД; 2 - а = 0.2; 3 - а = 0.5; 4 - а = 0.9

Задача №2. Рассматривается установившееся течение двухслойной смазки в зазоре радиального подшипника конечной длины. Вал вращается с постоянной угловой скоростью Q, а подшипниковая втулка неподвижна. Подача смазочного материала осуществляется в осевом направлении, а его вязкость выражается следующей экспоненциальной зависимо стью от давления:

(2.1)

Р/ = Ро,е

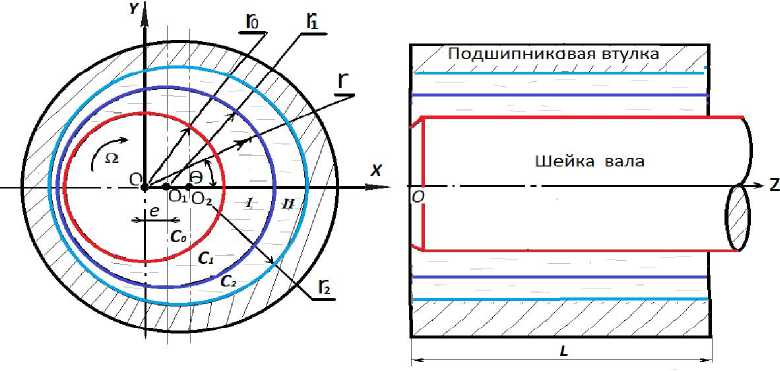
Рис. 2.1. Расчетная схема

В цилиндрической системе координат (г', 6, Э)с началом в центре вала уравнения контуров вала, границы раздела слоев и адаптированного контура опорной поверхности запишутся в виде:

С ¹ • к     f       V         СЧР А   СЧ Д А*

Q • ' — ' Q; ^1 • ' — ' 0

С ¹ • у' — у р ргхс А_ Д Qin m А    гттр   сч             v   v

2 . • —птсшйо  лашши,  1ДС  ис t [v_?ij_? о — л2  'О'

(2.2)

Исходные уравнения и граничные условия. Движение смазочной среды описывается системой уравнений движе. ния вязкой несжимаемой жидкости для приближения типа «тонкий слой» и уравнениями неразрывности

52иi        ~p сp   б 2wi        ~p сp i epip

2        ie          ,2ie          , r2                     r2             z

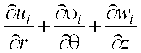
0 ( i   1, 2),

(2.3)

где размерные величины г', z', и-, и', р-, ц', описывающие распределение скоростей и давлений в смазочном слое, связаны с соответствующими стандартизированными величинами г, z, tq, ц, Pj, ц, соотношениями с' — г0 + Sr, z'— roz, mJ—Q?oWz, uj—Q/qU,, Ц — Q5z/, p’ — pgp, ц'—цОг-цг-.                 (2.4)

Здесь u^ и', mJ —компоненты вектора скорости смазочных сред; р’ — гидродинамическое давление в смазочных слоях; р_г- — динамические коэффициенты вязкости в смазочных слоях; а — экспериментальная постоянная;

Л; =

62pg

Но^Ф

p_g —характерное давление.

Граничные условия на поверхности вала и подшипника записываются в виде

«1 |_г=Г| = О, и, |_г=Г| = 1, 7^(0, z) = р(2п, z); ^ |_г=Г| = 0, /2(0,0) = 1, /2(0,1) = ^-_;

Pg и2 1г=Л(6)-0, и2 1г=Л(6)’ м’2 1г=Л(6)-0-

(2.5)

На границе раздела слоев граничные условия записываются в виде:

«1 1г-ой—«2 1г-«Л’ ^l 1г-оЛ— Ц? 1г-«Л’ ^1 Ir-oA-^2 1г-«Л’ ш, ,   _ ц2 5ог or ц1 or

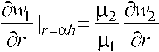
— 1г=аЛ=а/7'(9). и,

7/(0) =l + r]cos0-r]1sina>0, т| = е/5, гц =Н/5.

(2.6)

Граничные условия (2.5) означают прилипание смазки к поверхности вала и подшипника, периодичность гидродинамического давления, а также то, что при 9 = 0 давление задано в двух сечениях.

Условия (2.6) означают равенство скоростей, касательных и нормальных напряжений на границе раздела слоев, а также условие существования слоистого течения смазки, т. е. требуется, чтобы скорость точек границы раздела слоев в каждой точке была направлена по касательной к контуру раздела слоев.

Точное автомодельное решение. Точное автомодельное решение системы уравнений (2.3), удовлетворяющее граничным условиям (2.5) и (2.6), ищется в виде

А ^{=     + и}' ⁼ ^ ^{+ К(г}’⁰⁾’     = Hi,©, w, = w,C,9),

Ш             ОТ и^г,^ = -и^И(9>, У,(г^ = и,О. ^ = — /г(9)

~     ~  3                        6/ ~     ~  3

Л,е"“^;'=(-а)     —г ,² to + (-а)а, z, Л^е^-'⁴'= (-а) -Д—г ,² to + (-a)asz,

1 Д/гД) /ДеД 1    - Ц/гД) Дд)/ -

ных условий к ним

Д         Ф| /              Мгп

«1=«2^т «2=7—(А--!)- «1=—~«2*

Д      К          Moi

(2.7)

Подставляя (2.7) в (2.3), (2.5) и (2.6), придем к следующей системе дифференциальных уравнений и граниЧ'

Ч^СД t)' = q, 5^+^ =9, ч^=с2, ^=с^,

—— = 0^(6), —^ = 0^(6), Мх-|Дих=0; /->>- /            1      X Z z        z-s<^ /            Д,      X Z z        Д,      -j Д,         Z сЕр

Ф1(0) = 0; й1(0) = 0, и1(0) = 1, w1(0) = 0, ф'2(1) = 0, и2(1) = 0, и2(1) = 0, м2(1) = 0, u1(a) = u2(a), и1(а) = и2(а),

_ (А ~л / 3 Р                          _ М-02

— u2lar Til01) — ФгР^-Г С1 — С1Т с2 — с2т «1 —«2т

Mi                  Ml               Ml           MlMoi a1

из(а,9) = иу(а,9), —L e-a=——L      ui(O+ изСЖ=0.

oL ш oL J J

(2.8)

(2.9)

Учитывая, что разделение смазочного материала на слои происходит вблизи неподвижной твердой поверхности, т.е. при значениях а, близких к единице, условие раздельного течения смазки (и)(а)/ц(а)) = ай'(9) в принятом нами приближении удовлетворяется. На самом деле из граничного условия следует

iz72 (a) + au2 (a) + J u2 K№ = 0

(2.10)

и2(а)

иДад

-   +a + u2(a)

Г О2^М

J и2(а)

= 0.

(2.11)

Используя теорему о среднем значении, будем иметь

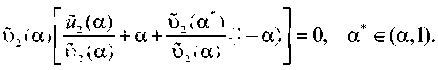
(2.12)

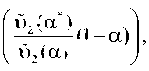
будем иметь

Так как u2(a*)< u2(a), (1 - a)«1, следовательно, с точностью до членов 0

ju^X^O, ^2M = 0.

0               a

Решение задачи (2.8)-(2.9) находится непосредственным интегрированием. В результате будем иметь

~  ~ E2

Vl =С2у + С2^ + Сз;

~   ~ E2

^2=C2 — +CA + C5,

S2

2 +c6-

—+ C8§

2    84,

^3     ^2

у-c6y + c10?

м^ = аД? ^ + d^, + d₂, w₂ = a₂l? у + d^, + d₃, ^3     ^2

^8       I^- H1'

р_х = с_хЛДУ) + с₂J₃ (9) + a_xz + b_A.

p2 =cxJ2(Q)+c2J3(6)+a2z+b2,

K_xe~^ap = A₁e~“

Л2е-“р =Л2е-°

e

- а[ J₂ (9)q + J₃ (9)с₂ ] - aqz, ‘ -a[J_?(9)q + J₃(9)c_?l-au_?z.

de

J (1+г] cos 9 - г], sin соб)4

(2.13)

Для определения постоянных _СД = 2,..., 11), d^j = 1,2,3,4), q, c₂, q, c₂ из 18 уравнений с 18 неизвестными:

решим следующую алгебраическую систему

r — 1 r — 0

% 1 J_

Cg — Cj Cg

= 0.

___                          C Cl _

0 i CoUC i Cq Co       C/iUC C< — I/.

С2

-1

^ 2 ^^

1

— 4 F Сд 4- C<

2 4 5

'     1 2

3     ^2

= 0.

g _ дЛ(2л) д₃(2л)

6      2

xa

^8

s; 1       1

Q 4" Cg 4~ Cg

6    2

Cl -L              Cl 4- Г' \ Г' С1 4-           Г' С1 4-    \

^Ш i G^ — tv UI I Cg )_у       Т Су — 'A\^2^^v^^4/>

7                     7 2           7        7                    7 А *-^         1              ТА *~av а^=е, a^h"— + d^+da =0, adi"--vdAa = adT--HAa + fld,

L VJv 1 vy J _? tv —       гч"

Pl

(2.14)

Решение системы (2.14) сводится к решению следующих двух матричных уравнений:

1ДС X л.|_? Сд_? С5_? Cg_? Cg к U ^U, ^А ОСД U₉ ^р

	М =	"      72(2л) 73(2л) 1 ka? - а" 4-1 J3(2.k) а2 (к-I)	2 0 0 2а(А: -1) 0	2 0 0 -2 0	0 2 Зки? - За2 4- 3 0 2а(к -1)	0 2 б-ба 0 -2
			N • у = т,
где y = \d1;d3;d4\ т = <	-----(a? - a.); n"alk(h		з ИЛ -аху,-а3 —
			а -а	-1
			N= 1 -к	0
			0 1	1

Решая матричные уравнения (2.15) и (2.16), с учетом (2.14), будем иметь

б + вка? - ба²

Л (2л)

_ J3 (2л) с4 -

(3 - ба2 - За4 - а р + 3^2а4 - б^а4)

(«Ас - а +1) А

_Зс/² Зс/ 4-3 4- 6Ата² ТА' 4- 3rLA'² ЗгСА^ СксС 4-LX^HLX HLX     HLX I I             A tv I HLX tv     -_/LX tv     LzALX I

_ 73(2л)

2                                (аА* - а +1) A та T^LX I                      ^LX I .ИХ i таА-LX AIvVa I 1                         ,

r* —__________________ r* —___________________________________ r* — c c — ur*

C§ —                ? Cg —                                ; C2 — ЛС4? Cg—/CCg?

A                   A

д —_1 + с/ ^_4- 4^c/_9     _4с/ 4- 6с/

LA — I LX I 1 I LX VAtvkA I та/vLX I tv LX I та/vLX z^aLX ^tLX I VzLX ^

Л(2л) 73(2л)

= 1 + -^-(COS27KB -1), 2лсо

14- -^- (cos 2лсо -1) 2лсо

~      ~   % Л(2л)                    h²

c,-kc,. Ct=-Ci— ---, «т=0, d^=-d_Д-a^—, 7₃(2л)                       2

1 А’2а г,

[Aro2ot - ^а 4-

^ _ 2 2 _____2_________

4             Ата - а 4-1

, d^ = kajh'd + d3k - a-JCei.

(2.16)

(2.17)

(2.18)

Определение основных рабочих характеристик подшипника. Для гидродинамического давления в принятом нами приближении приходим к следующему уравнению:

™ ~ 2ос                 . 1 2ac?.z „ an - 2 р 4- 2 - a--с, Д (6) 4- c7J3 (6)--— = 0.

Решая это уравнение, с точностью до членов 0(г],а),

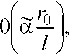
будем иметь

~

~

+ — [ c ~₁ J ₂ ( 9) 4- c ~₂ J ₃(6)14- - rv 12

a ₁ z

Л1

~ \

1 а I

14-— I.

(2.19)

Приведем гидродинамические силы, возникающие в смазочных слоях и воздействующие на вал, к центру вала О. Для ортогональных проекций безразмерного главного вектора этих сил, действующих на единицу длины вала,

главного момента и момента сопротивления осевому движению, получим выражения

^о

2тс

[ р^ sin 9^/9, R_x = - ^* , ^и о                 ' ^б"

р_г cos 979,

Др

Др^ г Г у" (О , ДД)) I р^о³ Д/7²(9)  /7(9) J"”

Др.осЭ Г 1 Tn’i

^Q J^9)T^

1=^о de.

Выражения для расходов смазочной жидкости в окружном и в осевом направлениях, записанные в нормализованной форме, будут иметь следующий вид:

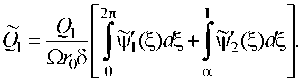
(2.20)

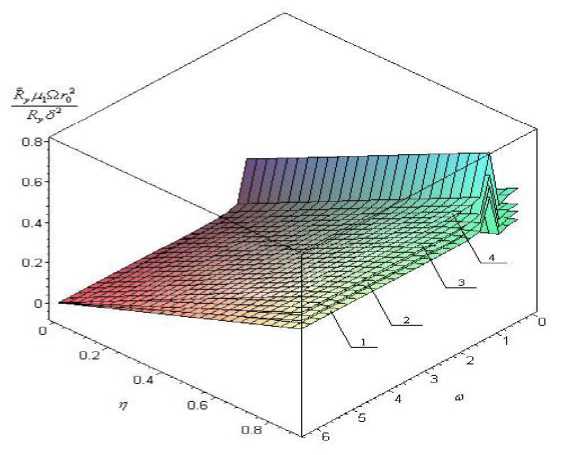
Рис. 2.2. Зависимость величины безразмерной несущей способности

/ДДУ2

ЛуО

от параметра расслоения смазочного материала р

и параметра адаптированного опорного профиля со при значениях вязкостных параметров: 1 - а = 0,1, k 2/ k 1 = 1; 2 - а = 0,3, k 2/ k 1 = 1; 3 -а = 0,5, k 2/ k 1 = 1,2; 4 - а = 0,9, k 2/ k 1 = 1,3

Проведение качественного анализа полученных аналитических выражений (2.20) для основных эксплуатационных характеристик узла трения позволяет сделать следующие выводы:

• -    компонента R_y безразмерной поддерживающей силы существенно зависит от вязкостного параметра а и вязкостных отношений k 2/ k 1;

• -    в рамках принятых предположений максимум несущей способности достигается при значении параметра

х 1

опорного профиля (0 = — ;

• -    учет зависимости вязкости от давления приводит к повышению расчетной несущей способности.

• -    в рамках принятых предположений, с увеличением значений вязкостного параметра а, сила сопротивления для осевого движения смазочного материала увеличивается.

Рассмотрев расчетные модели радиальных подшипников можно сделать следующие выводы:

• -    анализ полученных расчетных моделей радиальных подшипников с круговым опорным профилем, работающих на вязком несжимаемом смазочном материале при его двухслойной стратификации, позволил установить, что как обычные подшипники, так и подшипники с пористым покрытием на шейке вала имеют зависимость несущей способности от параметра вязкости смазочного материала а, вязкостного соотношения его стратифицированных слоев k2

  
  

и параметра а, разделяющего слои. Причем с ростом этих параметров величина несущей способности подшипника увеличивается, а при значении а = 0,2 имеет максимум;

• -    расчетные модели конечных и бесконечноразмерных радиальных подшипников, с адаптированным к условиям трения опорным профилем и двухслойным стратифицированным вязким смазочным материалом при зависимости его вязкости от гидродинамического давления, показывают при анализе, что несущая способность подшипников увеличивается с ростом вязкостного параметра а, параметра ц и параметра опорного профиля го, при значении которого го = 0,5 несущая способность имеет максимум;

• -    Теоретические исследования модели радиального подшипника, смазываемого материалом с двумя стратифицированными слоями, один из которых является вязким, с зависимостью вязкости от гидродинамического давления, а другой обладает вязкопластичностью, позволили установить, что несущая способность подшипника растет с увеличением параметра вязкости а, параметра стратифицированных слоев а (при а = 0,2 имеет место максимум) и параметра пластичности Л .