Structural inhomogeneity of metallic materials and quality criteria

Modern materials science focuses on studying the relationship between the structure of materials and their physical and mechanical properties [1]. The material's structure is the primary factor determining its properties [2], making the investigation of these relationships one of the key tasks in materials science [3]. However, this process is accompanied by several challenges, including the limitations of existing theoretical models [4], [5] and the insufficient accuracy of property predictions based on known structural parameters [6]. This issue is further exacerbated by the inaccuracy and limited representativeness of data obtained through traditional laboratory experiments [7].

The rapid development of modern non-destructive material quality control methods has been made possible by advancements in scientific research and improvements in computer technologies [8]. These advancements offer new opportunities to analyze the mechanisms underlying the formation of material properties, such as those of metals and alloys. Applying these approaches not only deepens the understanding of the patterns that govern material behavior but also enables the development of improved technological processes [9]. Furthermore, the use of cutting-edge methodologies facilitates the identification of complex relationships between individual structural elements [10],[11], their microscopic characteristics, and macroscopic mechanical properties [12].

Such studies have both fundamental and applied significance, as their results can be utilized to create innovative materials with tailored properties, contributing to progress across various industrial sectors.

Investigating the relationships between the structure and properties of low-carbon low-alloy steels is particularly important, as these materials are widely used in manufacturing critical components across multiple industries [13], [14]. The mechanical properties of such steels can be effectively enhanced through thermal and thermomechanical treatment methods. These technological processes induce significant structural changes, leading to complex transformations within the material.

The diversity of structural forms, their intricate geometrical configurations, and the non-trivial spatial arrangement of structural elements pose substantial challenges in selecting appropriate tools for quantitative analysis [15], [16]. These factors underscore the relevance of this research.

The application of multifractal theory represents a promising approach to advancing modern nondestructive control methods [15]. This theory enables the evaluation of the mechanical properties of metals by analyzing structural elements of high complexity that do not conform to traditional Euclidean geometry. The latter relies on integer characteristics, which limit the analysis of complex structures [17,18].

Thus, alongside conventional geometrical characteristics (e.g., structure rating, grain diameter, cross-sectional area) and statistical indicators (e.g., the number of micro-particles per unit area of the section), methods based on dimensional spectrum analysis are actively being developed [19], [20]. As noted by many researchers, this approach opens new opportunities for studying the structure of steels and cast irons.

This study proposes a method for non-destructive evaluation of the mechanical properties of low-carbon low-alloy steel after thermal treatment. The method is based on the multifractal concept, enabling more accurate property predictions and expanding the existing arsenal of analytical tools.

• 2    Materials and Methods

The subject of this study is the fractal dimension of the structural elements of low-carbon steel. The primary objective was to identify a clear correlation between the hardness of the metal and the fractal dimension of its microstructure. The choice of this steel is justified by the availability of detailed information about its structural characteristics. The steel’s microstructure underwent thermal treatment, which allowed the formation of a set of parameters (phase components). The material selected for the study was a low-alloy low-carbon steel with the following chemical composition (in mass percent): C – 0.115%; Si – 0.29%; Mn – 0.39%; P – 0.012%; Cr – 0.12%; S – 0.026%; Cu – 0.215% [21–24].

The samples were subjected to thermal treatment at a fixed temperature of 920°C with a holding time of 300 seconds. The cooling process to 500°C was carried out over various time intervals. The ferrite-pearlite structure of the steel and the cooling parameters from 920°C to 500°C are shown in Figure 1.

a                 b                 c                 d                   e

Fig. 1 - Microstructure of low-carbon steel, (×200)

Figure 1a shows the microstructure consisting of 12% pearlite and 88% ferrite. The ferrite grain size corresponds to a grade of 5–6, with some areas showing a grade of 4. To reach a temperature of 500°C, the cooling process lasted for 26 hours. Figure 1b presents ferrite grains and pearlite regions, with the ferrite content at 88% and pearlite at 12%. The ferrite grain size ranges from grade 6 to grade 7. Cooling was carried out over 8000 seconds. Figure 1c illustrates a structure with 87% ferrite and 13% pearlite, where the ferrite grain size corresponds to grades 6 and 7. Cooling was achieved in 920 seconds. Figure 1d depicts a heterogeneous structure. In addition to the fine-grained ferrite with small regions of pearlite, areas of ferrite and pearlite are visible, forming a Widmanstätten structure. The ferrite content is 83%, and pearlite is 17%. In the fine-grained areas, the grain size reaches grade 9. The cooling time to reach 500°C was 29 seconds. Figure 1e shows a structure consisting of 86% ferrite and 14% pearlite, with small sections of bainitic structure. Cooling to 500°C took 62 seconds.

• 3    Results and Discussion

For the quantitative analysis of structural changes occurring during thermal treatment, the multifractal theory was employed [25]. This approach enables the investigation of the distribution of various material characteristics, including physical, geometric, mechanical, and chemical properties, through the lens of the universal concept of measure [26]. The fundamental principle involves partitioning the space containing the studied object (the measure carrier) into geometric shapes with integer Euclidean dimensions, such as squares, cubes, or circles, of a defined size.

During the research, a geometric construction method of measure was used, which involves approximating linear and area elements of the structure. Such elements include grain ensembles, interfacial and intraphase boundaries, as well as bainitic structures. Square cells were used for approximation, covering the structural elements.

One of the key parameters calculated during the analysis is the Hausdorff-Besicovitch dimension, D ₀ , also known as the box-counting dimension [27-29]. Its determination was based on a bilogarithmic relationship between the number of square cells, N ( 5 ) , required to cover the studied object, and their linear size, δ . This approach allows for the effective description of complex and diverse structural forms that are characteristic of materials subjected to thermal treatment.

D o =

In N ( 5 )

- lim------

5 ^ 0   ln 5

The reliability of the box-counting method for calculating dimensionality is confirmed by its extensive application in various fields of natural sciences [30]. This method allows for the determination of the dimension of objects with complex geometric structures with minimal time expenditure, making it particularly relevant for the quantitative evaluation of the real structure of metals and alloys across different scale levels.

The use of the box-counting method is justified by the fact that many natural and artificial objects exhibit fractal properties, especially in intermediate asymptotic ranges. In this domain, the surfaces of such objects are no longer smooth but have not yet reached the scale of interatomic distances [31]. This makes it possible to effectively describe such structures based on the concepts of fractal geometry.

For the multifractal parameterization of digital images of the microstructure, a statistical sum was introduced, based on a collection of nested fractal sets with variable dimensions. This sum is formulated to account for the influence of structural inhomogeneities at various scale levels. The parameter q, known as the degree exponent, can take values in a broad range from -∞ to +∞ , enabling the capture of both small and large structural features.

The application of this statistical sum allows for a detailed description of the microstructural properties of the material through the analysis of multifractal characteristics. For each structural image, two key multifractal spectra were calculated:

• 1.    The Renyi spectrum D ( q ) (2) - characterizes the relationship between fractal dimension and the degree exponent ( q ) . This spectrum describes how the mass density distribution changes across various scale levels. Each dimension of the spectrum D ( q ) has a well-defined physical meaning, reflecting structural properties such as packing density or the degree of inhomogeneity.

• 2.    The f ( a ) spectrum (3) - defines the fractal dimension of a set with a given local density exponent α . This spectrum describes the distribution of local densities within the structure, indicating the prevalence of specific scale characteristics.

To calculate the spectra D ( q ) (2) and f ( a ) (3), a statistical sum was used, constructed based on dividing the image into cells of varying sizes. In each cell, the local density distribution is assessed, and then parameters dependent on the value of ( q ) are calculated. This approach enables effective analysis of areas with high structural element density as well as zones with low concentration:

• 1       ^ln N p q

D ( q ) =-- lim ——— q - 1 3 ^ In 3 ’

where, δ refers to a cell, which serves as the elementary unit of the square grid used to cover the studied object for calculating its fractal dimension. The grid is employed to divide the structure under investigation into equal segments, and this parameter enables the quantitative measurement of the object's fractality. The probability p_i represents the likelihood that a point (or pixel, in the case of digital images processed using computational methods) of the studied object will fall into the i - th cell of the square grid with size δ . This parameter describes the uniformity or non-uniformity of the distribution of structural elements across the studied area, helping to identify potential micro-level inhomogeneities.

The fractal dimension spectrum is determined through the Legendre relation, which is used to convert information from the statistical sum into fractal dimensions. This relation allows expressing the connection between the fractal dimension of the set and its contribution to the statistical sum at various values of the parameter q . Through this spectrum, one can analyze how the packing density of structural elements changes across different scales and assess their degree of fractality, which is crucial for understanding the material's mechanical properties.

^{f ( a} ) = q • ^a - ^{t (} q ) = q •- ^{t (} q ) dq

where α represents the Hölder exponent, a constant for fractals, with numerical values coinciding with

N

In S Pq the fractal dimension D0, and т(q) = - lim ——— is a characteristic representing the density of the cells δ→∞ In 3

occupied by elements of a single phase or constituent.

The resulting multifractal spectra provide the means to establish a correlation between the structural parameters of the material, such as grain size, phase content, and the heterogeneity of their distribution, and hardness. Thus, multifractal analysis offers a powerful tool for a comprehensive study of the influence of microstructure on the operational characteristics of steels and other materials.

• Figure 2 shows the calculation of the multifractal dimension spectrum for the pearlitic structure presented in Figure 1a. Using specialized software (Figure 2a), which operates in a 256-color format, the chosen calculation parameters are illustrated in Figure 2b.

  
  
  
  
  
  

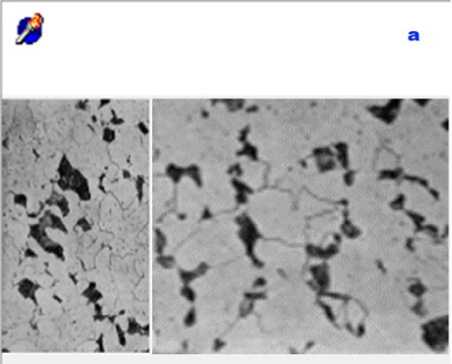
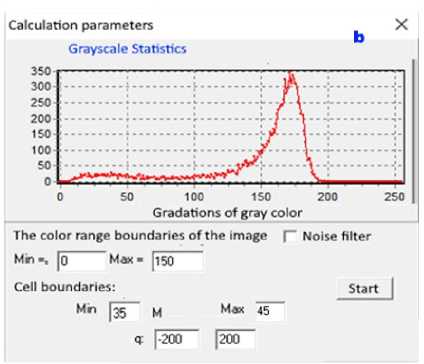
4                                                                   2                         3

Fig. 2 - Calculation of the multifractal spectra D(q) and f(α) for the metal microstructure

The following parameters were used in the study: Hausdorff-Besicovitch dimension D ₀ , the homogeneity index f , calculated for degree exponents q _min = - 100 and q _max = 100 , as well as the coefficients of dimensional change for the most densely packed structural elements D _{- 100} and the least densely packed elements D ₁₀₀ : ∆ D = D _{- 100} - D ₁₀₀ . Their physical characteristics are as follows:

• 1.    The dimension D ₀ is a purely geometric parameter calculated based on the structural features of the system. Various methods of calculating this parameter generally yield similar results for physical systems. In the physical context, this parameter reflects the compactness of the object’s occupancy in space and the complexity of the object's boundaries. From a materials science perspective, it provides insight into how «complex» or «twisted» the material's structure is.

• 2.    The homogeneity index f ( α ) represents a statistical measure of the distribution of structural elements. Unlike traditional approaches focused on qualitative descriptions of appearance, this parameter quantifies the uniformity of distribution of elementary units (e.g., points or pixels for computerbased analysis) across different regions, assuming that geometrically identical elements of a fractal set are occupied by points with equal probability.

In the context of materials science, the parameter f ( α ) is used to assess the local defectiveness of structural elements, which is crucial for understanding the mechanical properties of the material. Homogeneity not only characterizes the appearance of the structure but also serves as an indicator of defect distribution across different phases of the material. The Renyi dimension spectrum, presented in Figure 2a, was used to calculate these parameters. Homogeneity f was determined by evaluating the deviations of the edge parts of the spectrum f ( α ) from zero:

• a)    The deviation of the left part of the spectrum indicates the degree of homogeneity of the most densely packed cells in the structure, which contain dark elements, such as pearlite. This deviation serves as an important indicator of the distribution of phases with high density.

• b)    The deviation of the right part of the spectrum characterizes the homogeneity of the less saturated (lighter) cells, where ferrite predominates. This deviation helps evaluate the degree of defectiveness in such areas of the structure, which also impacts the material's mechanical properties.

Thus, the homogeneity parameter f ( α ) is a powerful tool for studying local variations in structure and their correlation with the physical and mechanical properties of the material.

Multifractal characteristics provide a deep understanding not only of the external appearance and macroscopic structure of a material but also of its internal microstructure [32]. For example, numerous applied studies [33–35] have demonstrated that the dimensional spectrum of structural elements in metals, as well as the interphase boundaries, exhibit a clear relationship with their mechanical properties. This includes the impact on characteristics such as hardness, tensile strength, and fatigue resistance.

As a result of the analysis of experimental data, graphs were constructed that show the relationship between structural elements, expressed through multifractal indicators D ₀ , D _{- 100} , D ₁₀₀ and f ( α ) , and the hardness of the material, HV (Figure 3).

Fig. 3 - Relationships between the multifractal spectrum indicators and the hardness of the metal

).0029x +1.151

R2 = 0.9228

0043x + 0.6757

i2 = 0.8774

Research has demonstrated a consistent decrease in hardness with increasing fractal dimensionality of ferrite (Fig. 3a) and a corresponding increase in the fractal dimensionality of pearlite (Fig. 3b). This phenomenon arises from the prolonged cooling time of the metal to 500°C, which extends from an initial 29 seconds to 26 hours. The observed relationship confirms that cooling significantly influences the microstructure and mechanical properties of steel.

As is well known, the pearlitic transformation proceeds via a diffusion-controlled mechanism. Prolonged cooling leads to substantial modifications in the material's microstructure, reflected in the development of more regular geometries among its constituents. Under slow cooling conditions, structural components exhibit enhanced symmetry and organization, which, in turn, improve structural compactness and phase distribution within the polished cross-section plane. This transformation process results in a marked increase in fractal dimensionality, approaching the Euclidean dimensionality of 2 during extended cooling. This increase indicates a higher degree of spatial organization within the structure, which is critical for understanding how thermal treatment affects the material's properties. The increased symmetry and order of ferrite (Fig. 3c) and pearlite (Fig. 3d) directly enhance the mechanical characteristics of the material, such as hardness and, consequently, strength.

These findings are particularly important for studying the impact of thermal treatment on the material's physical and mechanical properties. Thus, the identified dependencies underscore the importance of optimizing cooling regimes to control steel properties, which could inform the development of advanced thermal treatment technologies aimed at targeted property modifications.

The homogeneity of f ( a ) in ferritic (Fig. 3e) and pearlitic (Fig. 3f) components exhibits pronounced sensitivity to variations in thermal treatment regimes. This parameter, along with fractal dimensionality and regularity indices, tends to increase with longer cooling durations. Slow cooling promotes a more uniform redistribution of iron and carbon atoms due to activated diffusion mechanisms, resulting in greater dimensional homogeneity of both pearlitic and ferritic phases.

• 4    Conclusions

Based on the conducted research, it was established that the fractal dimensionality D ₀ , regularity ( D _{- 100} - D ₁₀₀ ), and homogeneity f ( a ) exhibit a consistent tendency to increase as the cooling time of low-carbon low-alloy steel extends from 29 seconds to 26 hours at temperatures ranging from 500°C to 920°C. These findings highlight the high sensitivity of metal hardness to the multifractal characteristics of its structure:

• 1.    The observed increase in fractal dimensionality and regularity with prolonged cooling underscores the critical role of thermal treatment in determining the structural complexity and spatial organization of the material.

• 2.    The established relationships can be utilized to predict and optimize quality criteria for this class of steels. Specifically, by controlling cooling parameters, it is possible to influence the material's microstructural features, thereby improving its performance characteristics.

• 3.    The multifractal approach demonstrates significant promise as a tool for analyzing and controlling structural transformations in metals under varying thermal regimes. It offers a robust framework for linking microstructural attributes to macroscopic mechanical and physical properties.

These findings emphasize the importance of cooling regime regulation as a means to tailor material properties to specific application requirements, ensuring enhanced operational performance and compliance with mechanical and physical standards.

• 5    Fundings

  This research was partially by Ministry of Science and Higher Education of Russian Federation (funding No FSFM-2024-0025).