Structure, interactions and kinetics of ring-like formations of carbon nanotubes (nanofibers) in polymer nanocomposites

DOI:

Aims and Background degree), typical for the indicated nanofillers, result in formation by them of ring-like structures, outwardly resembling macromolecular coils [13; 17]. This circumstance has already been noted in literature. So, the authors [13] assumed, that carbon nanotubes ring-like structures can be considered as macromolecular coils in

As it is well-known [12], carbon nanotubes (nanofibers) possess very high longitudinal elasticity modulus (1000-2000 GPa) and low transverse stiffness. These factors together with a large ration length/diameter (high anisotropy semidiluted solutions. The authors [8] used Flory formula for rod-like macromolecules in case of carbon nanotubes percolation threshold in polymer nanocomposites determination. Nevertheless, such examples are rare enough and do not have systematic character.

It is obvious, that formation process of carbon nanotubes (nanofibers) ring-like structures can not be instantaneous for example in virtue of the polymer melt high enough viscosity, in which these structures are formed. Hence, the indicated process has definite duration, that makes necessary its kinetics study. Therefore purpose of the present work is the study of intercommunication of interactions, formation kinetics and structure of ringlike formations of carbon nanotubes (nanofibers) in polymer nanocomposites.

Experimental

Polypropylene (PP) “Kaplen” of mark 01030 was used as matrix polymer for the studied nanocomposites. This PP mark has a melt flow index of 2.3-3.6 g/10 min, molecular weight of ~ (2-3) х 10 5 and polydispersity index of 4.5.

Carbon nanotubes (CNT) of mark “Taunite”, having an external diameter of 20-70 nm, an internal diameter of 5-10 nm and length of 2 mcm and more, were used as a nanofiller. In the studied nanocomposites PP/CNT taunite content was varied within the limits of 0.25-3.0 mass %. Besides, the multiwalled nanofibers (CNF) were used, having a layers number of 20-30, diameter of 20-30 nm and length of the order of 2 mcm. In the nanocomposites PP/CNF CNF content W_n was varied within the limits of 0.15-3.0 mass %.

Nanocomposites PP/CNT and PP/CNF were prepared by the components mixing in melt on twin screw extruder Thermo Haake, model Reomex RTW 25/42, production of German Federal Republic. Mixing was performed at temperature 463-503 K and screw speed of 50 rpm during 5 min. Testing samples were prepared by casting under pressure method on a casting machine Test Samples Molding Apparate RR/TS MP of firm Ray-Ran (Taiwan) at temperature 503 K and pressure 43 MPa.

Uniaxial tension mechanical tests have been performed on the samples in the shape of two-sided spade with the sizes according to GOST 112 62-80. The tests have been conducted on the universal testing machine Gotech Testing Machine CT-TCS 2000, production of German Federal Republic, at temperature 293 K and strain rate of ~ 2 х 10-3 s-1.

Results and Discussion

CNT (CNF) ring-like structures radius R _CNT can be determined with the aid of the following percolation relationship [6]:

Ф n

CNT r CNT ( ^{2 R} CNT )

where j _n is nanofiller volume contents, L _CNT and r CNT are length and radius of carbon nanotube (nanofiber), respectively.

The value j _n was calculated according to the well-known formula [11]:

W

» n = .,                   (2)

Pn where Wn is nanofiller mass contents, pn is its density, estimating for nanoparticles as follows [ibid.]:

P n = 188 ( D CNT ) ^1/3, kg/m^{3 ,            (3)}

where D _CNT is a carbon nanotube (nanofiller) diameter, which is given in nm.

A CNT (CNF) ring-like formations structure can be characterized most exactly with the aid of its fractal dimension D_f , which is true structural characteristic, since it describes the distribution of CNT (CNF) ring-like formations elements in space [ibid.]. The value R _CNT calculation according to the equation (1) has shown its reduction at j _n growth. At the largest from the used j _n values, corresponding to W_n = 3.0 mass %, the indicated dependences have the tendency of asymptotic branch achievement, that supposes achievement by CNT or CNF ring-like structures of their R _CNT minimum values. By the analogy with macromolecular coils this means the achievement of maximally dense ring-like structure with the greatest limiting value of its fractal dimension D_f ( D ^l _f ^im ), which is determined according to the equation [7]:

D lim _ ⁴ ( d + 1 )

f 7 ,

where d is the dimension of Euclidean space, in which a fractal is considered (it is obvious, in our case d = 3). For d = 3 the value D ^l _f ^im =2.286.

Further for the value D_f estimation the irreversible aggregation model can be used, which describes polymerization processes (macromolecular coil formation) and gives the following relationship for particles aggregates radius R_agr determination [16]:

R agr ~ С о"⁽ d - D f ⁾ , (5)

where c ₀ is aggregating particles initial concentration.

Coefficient in the relationship (5) can be determined at the following conditions: R_agr = R CNT , c 0 = j n and D f = D T- The values R _CNT and j _n were accepted for W n =3.0 mass %. As the estimations according to the indicated relationship have shown, the value D_f grows at j _n increasing ( R _CNT reduction) from 1.91 up to 2.29 for nanocomposites PP/CNT and from 1.76 up to 2.21 for nanocomposites PP/CNF.

As it is known [9], the process rate in fractallike medium is described by the following equation:

A ~ t "  h ,                    (6)

where t is process duration, h is medium heterogeneity exponent (0 <  h < 1), which is transformed into zero for homoheneous samples only [ibid.].

The value h was calculated according to the equation [10]:

h =

D f

—

In Fig. 1 the dependences of R _CNT on CNT (CNF) ring-like structures formation process rate J are adduced for the considered nanocomposites. As it was to be expected, the process rate J increasing results in R _CNT growth, i.e. the value J characterizes not CNT (CNF) rolling up in ringlike structures, but their unrolling. The dependence R _CNT ( J ) can be expressed analytically by the following empirical equations:

R _CNT = 90 + 5.0 x 10³ A           (8)

for carbon nanotubes and

R C _NT = 45 + 2.70 x 10 3 A           (9)

for carbon nanofibers. The parameters t in the equation (6) and R _CNT in the equations (8) and (9) are expressed in s and nm, respectively.

Let us note, that the smallest RCNT value according to the equations (8) and (9) is equal approximately to 2DCNT at J=0, since for the obvious reasons the condition RCNT = 0 is impossible. The greatest value RCNT in case of homogeneous mediums (h = 0) is equal to 5090 nm for CNT and 2745 nm for CNF.

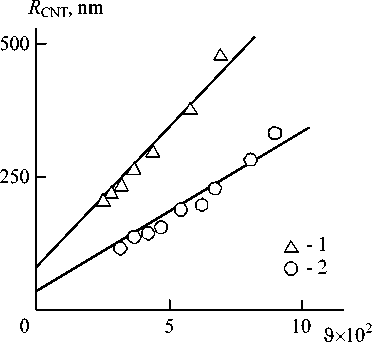
Fig. 1. The dependences of CNT (CNF) ring-like formations radius R _CNT on their unrolling rate J for nanocomposites PP/CNT ( 1 ) and PP/CNF ( 2 )

Let us consider the intercommunication of CNT (CNF) ring-like structures formation rate J and interaction between them. At the indicated structure modeling as macromolecular coils the interaction between their elements and polymer matrix can be characterized by the parameter e , determined as follows [10]:

e =

2 “ Df Df

.

For macromolecular coils the value e is varied within the limits of-1/3 + 1.0. In the point Df = 2.0 parameter e changes its sign, that corresponds to the interactions type change from repulsion forces (positive e) up to attraction forces (negative e). In Fig. 2 the dependence of CNT (CNF) ring-like structures formation rate J on interaction parameter e is adduced for the considered nanocomposites. As one can see, the linear dependence of CNT (CNF) ring-like structures unrolling rate J at e increasing is obtained, i.e. the repulsion interaction intensification, which is described analytically by the following empirical equation:

A = 0.275 ( e + 0.215 ) .         (11)

From the equation (11) it follows, that the value J = 0 is achieved at e = -0.215, i.e. at Df =2.548. The greatest value J = 0.334 is realized at e = 1.0, that corresponds to h = 0.192 or Df = 1.384.

growth. This dependence can be expressed analytically by the following empirical equations:

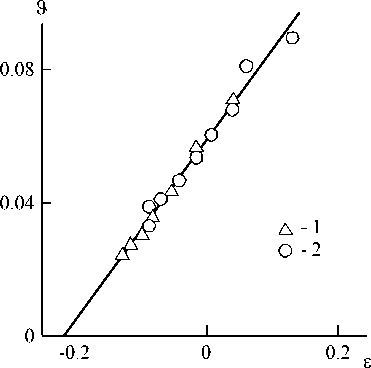
Fig. 2. The dependence of CNT (CNF) ring-like structures unrolling rate J on interaction parameter e for nanocomposites PP/CNT ( 1 ) and PP/CNF ( 2 )

e = 0.25 - 0.85 ф ’ „ ^/4             (12)

for carbon nanotubes and e = 0.25 - 0.85фП,4            (13)

for carbon nanofibers.

The equations (11)-(13) combination demonstrates, that for the considered nanocomposites e variation is realized within the range, which is smaller than theoretical one for macromolecular coils ( e = -1/3 + 1.0), namely, within the limits of e = -0.215 + 0.30. The condition of full balance of attraction and repulsion forces for CNT (CNF) ring-like structures e = 0 is realized at j _n = 0.0075 for nanocomposites PP/CNT and j _n =0.0155 for nanocomposites PP/CNF.

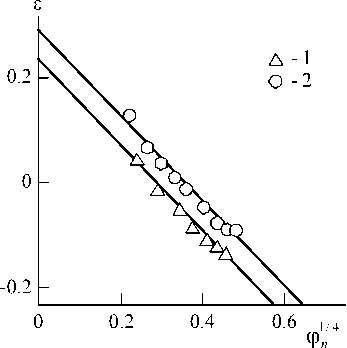
Fig. 3. The dependences of interaction parameter e on nanofiller volume contents j n for nanocomposites PP/CNT (1) and PP/CNF (2)

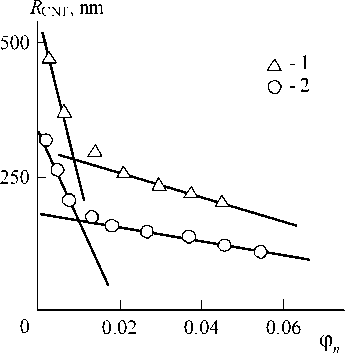
Fig. 4. The dependences of CNT (CNF) ring-like formations radius R _CNT on nanofiller volume contents j _n for nanocomposites PP/CNT ( 1 ) and PP/CNF ( 2 )

As it is noted above, nanofiller contents j n increasing results in dimension D_f enhancement and, according to the equation (10), in the exponent h increasing, i.e. in medium heterogeneity degree enhancement. In Fig. 3 the dependences of parameter e on the value ф ' _п ^/4 (such form of the indicated dependences was chosen for their linearization) are adduced for the considered nanocomposites. As one can see, e linear reduction is observed, i.e. the attraction interactions intensification, at nanofiller contents

In Fig. 4 the dependences RCNT(jn) are adduced for the indicated nanocomposites, each one from which can be approximated by two straight lines with enough precision degree. The transition between these two parts of the dependences RCNT(jn) corresponds to jn» 0.0088 for nanocomposites PP/CNT and jn» 0.0120 for nanocomposites PP/CNF, that agrees well enough with the indicated above jn values, at which the condition e = 0 is achieved or, in other words, with values jn, at which the transition from attraction interaction up to repulsion interactions of CNT (CNF) ring-like structures is realized. The linear dependences RCNT(jn) slope is in about 15 times larger in case of the repulsion interactions in comparison with the attraction interactions. In other words, in case of interactions first type much more fast RCNT growth at jn reduction is observed, that influences positively on the characteristics of nanocomposites polymer/ carbon nanotubes [17]. This effect explains the indicated nanocomposites relatively high reinforcement degree at ultrasmall concentrations (jn£ 0.0015) of carbon nanotubes [5; 8].

Conclusions

Thus, in the present work the results have shown that the formation (unrolling) rate of carbon nanotubes (nanofibers) ring-like structures in polymer nanocomposites can be described within the framework of fractal kinetics, where the indicated rate is defined by interactions level in these structures. A medium heterogeneity level or interactions degree and sign is controlled by nanofiller contents. The transition from attraction interactions up to repulsion interactions defines carbon nanotubes (nanofibers) ring-like structures radius fast growth, that results in nanocomposites relatively large reinforcement degree at ultrasmall contents of the indicated nanofillers.