Струйная модель микрореактора в микрофлюидных аналитических системах

В работе [1] приводится постановка задачи о микрогидродинамической струйной модели в проточных аналитических системах. Предварительная оценка числа подобия Re, характеризующего влияние инерционных сил, показывает, что эти силы в микрофлюидных системах могут быть значительны [2]. В развитие работы [1] ниже рассматривается модель струйного микрореактора. Проводится анализ ее особенностей относительно классического подхода на основе профиля Пуазейля.

Список обозначений d — диаметр капилляра;

v _p — электрофоретическая подвижность частиц пробы;

е ₀ — электрическая постоянная;

е — диэлектрическая проницаемость буфера;

Z — электрокинетический потенциал;

Е — напряженность электрического поля;

ц — динамическая вязкость буфера;

Ф — потенциал внешнего электрического поля;

L — длина капилляра;

D — коэффициент диффузии;

р — плотность буфера;

r — радиус частиц;

T — температура буфера, реагента, пробы;

E 1 — энергия активации;

• R — газовая постоянная;

• u , v — продольная и поперечная компоненты скорости частиц пробы, реагента;

• х , у — продольная и поперечная координаты;

• q — заряд;

• Y 1 — плотность заряда;

Q — тепловой эффект реакции пробы и реагента;

W — скорость химической реакции пробы и реагента;

k ₊, к _- — постоянные скоростей химических реакций, соответственно прямой и обратной;

C 1 , С ₂, С ₃ — концентрации пробы, продукта, реагента соответственно;

с _р — теплоемкость при постоянном давлении;

F — поток теплосодержания пробы, реагента;

G — массовый расход пробы, реагента;

Da — число Дамкеллера (соотношение гидродинамической длины и длины реактора);

• р , m 1 , N — параметры реологии смеси (р = = 1/(2 N - 1));

• Y — интенсивность тепловыделения в ходе химической реакции;

• т — касательное напряжение в потоке;

• P — давление в потоке;

• § — толщина микроструи;

A T = T - T „ — разность температур смеси в капилляре и температуры стенки капилляра;

• а = р — реологический фактор;

в — безразмерный тепловой эффект химической реакции.

ОПИСАНИЕ МОДЕЛИ

С учетом оценки характерных величин физико-химического процесса можно сформулировать следующую струйную модель микрореактора:

д и

д и

р • и--+ р • v--= дx       ду

д P 1

д (

---1-------------------- дx  у ду

V

у Г1+ F q , д у

Р .^И. + р .^J^ = 0, дx         ду

F = q • E , ^ф = ^- Y 1 ——,

. q                                 Е 0 • Е

Продолжение системы (1)

Начальные условия:

p • c_n • u --A T + p • c_n • v --A T =

^P p     d x         p     д y

y

д дУ

V

y — A T ^д У

⁺ Q i ,

u = u 0 ,

C i = C° ( C i ⁰ = const, i = 1,3), - для | y | <  d ;

C₂ = 0, x = 0

2 (3)

u = 0, C i = 0                      для | y | >  d .

Q i = Q • W ,

W = ( - k + • C 2

• C + k • C

3     —

'2 ) •

( exp

V

1 + у •A T

т = m 1

(д u ^ d y

V J 7

•

d u ^д У

N - 1

,

д C i

d C       d C p • u--i- + p • v--i- = дx        дy

D д ( д C ) yi-

У д y V   д y 7

+ ( — 1) i ,

i = 1,2,3.

Рассматривается реакция второго порядка, то есть концентрации реагента и пробы одной величины, зависимость от температуры предполагается аррениусовской, кроме того, учтено влияние распада продукта на скорость химической реакции.

Целесообразно отметить, что использование уравнений пограничного слоя обусловлено тем, что длина капилляра много больше его характерного поперечного размера, то есть продольный масштаб много больше поперечного. Можно показать, что в этом случае вторые производные от скоростей, температур и концентраций пробы и реагента по продольной координате малы по сравнению со второй производной по поперечной координате.

Граничные условия задаются для струйного течения. Наличие инвариантов струйного течения позволяет получить численное решение трехмерной задачи при автоматическом контроле счета.

Граничные условия:

u = 0, Ci= 0, AT = 0, y ^~, du=0, дА=0, ^=0, y=0.   (2)

,,   , дy      дy        дy

Интегральные соотношения для системы уравнений (1) с учетом условий (2, 3) имеют вид:

для импульса

те                     те p • J u2 • y • dy =J Fq • y • dy, для потока избыточного содержания те p • cp •J u • AT • y • dy = const = F0 i, для массового расхода те p •J u • Ci • y • dy = const = G 0 i, i = 1,3.

Метод локального подобия (МЛП):

u = um • f'(Ф1),  Ф1 = ^TT , o (x)

C i = C mi (x ) • 0 1 ( Ф 1 ),                         (5)

A T = A T m ( x ) • ^ ( Ф 1 ),

где индекс m — для величин на оси капилляра, — позволяет получить уравнения для изменения масштабных величин вдоль оси капилляра струйного микрореактора (СМР).

СЛУЧАЙ РЕАКЦИЙ 1-ГО ПОРЯДКА

В случае реакции первого порядка система (1) с использованием МЛП (5) будет иметь вид:

d F       F

— = exp(----------) • в • Da^ G • xp, dx    V 'xp + Y • F dG = — exP( p F _) • Da G • xp,        (6)

dx        xp + Y • F um (x) = x—p, 8 (x) = xp

(массовые силы полагаются незначительными).

Граничные условия соответствуют разогреву холодной смеси в ходе химической реакции: F (0) = 0; G (0) = 1.

Результаты расчета представлены на рис. 1–3. Обозначения: U ^{〈 1 〉} — расстояние ( x ) вдоль оси капилляра; U ^{〈 2 〉} — изменение массового расхода ( G )

вдоль оси капилляра; U ^{〈 3 〉} — изменение потока теплосодержания ( F ) вдоль оси капилляра (все величины безразмерные).

Увеличение времени пребывания в микрореакторе приводит к формированию резкого фронта пробы (рис. 1)

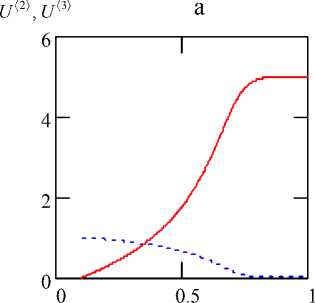
Рис. 1. Изменение вдоль оси параметров СМР: а — β = 5, Da = 0.5, γ = 0.05, α = 0;

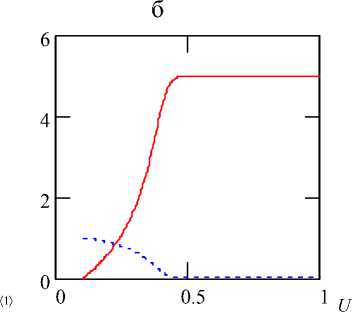
б — β = 5, Da = 1, γ = 0.05, α = 0;

в — β = 5, Da = 1.5, γ = 0.05, α = 0.

_U 〈 2 〉 _{, U} 〈 3 〉

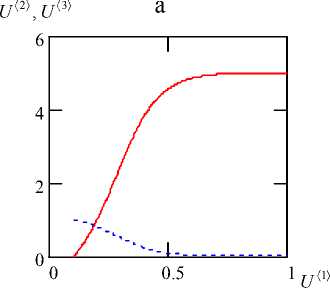
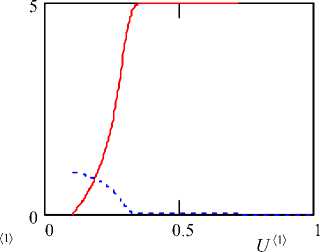
Рис. 2. Изменение вдоль оси параметров СМР: а — β = 5, Da = 1.5, γ = 0.3, α = 0;

б — β = 5, Da = 1.5, γ = 0.3, α = 1;

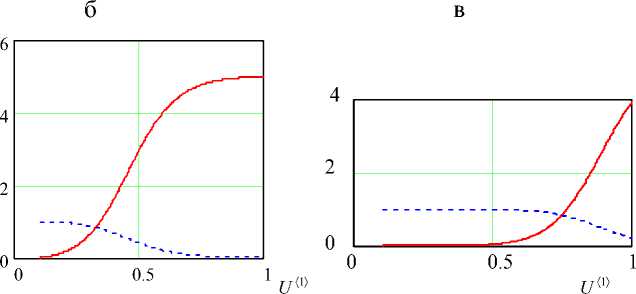
в — β = 5, Da = 1.5, γ = 0.3, α = 5.

_U 〈 2 〉 _{, U} 〈 3 〉

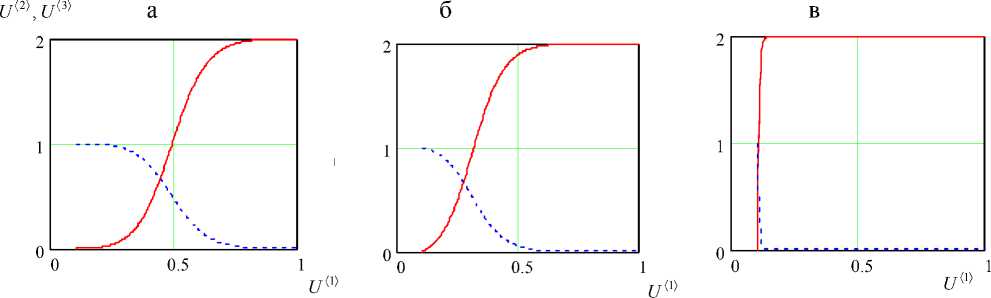
Рис. 3. Изменение вдоль оси па аметров СМР: а — β = 2, Da = 5, γ = 0.3, α = 2.5;

б — β = 2, Da = 5, γ = 0.3, α = 1;

в — β = 2, Da = 5, γ = 0.3, α = –1.5.

----------------- U ^(2>,

............... U ^<3>

На рис. 1, в и рис. 2, а проиллюстрировано отличие реакций типа горения ( γ = 0.05) от реакции типа окисления ( γ = 0.3).

На рис. 2 и рис. 3 виден эффект реологии пробы, реагента и буфера: α = 0 соответствует течению концентрированной суспензии, α = 1 — ньютоновской жидкости, а α = 5 — течению полимеров.

Видно, что измерение пробы полимеров приводит к более жестким требованиям по длине капилляра по сравнению с водой.

На рис. 3, в показано формирование резкого фронта пробы за счет реологического фактора, которое обусловлено физикой структуры полимеров, в частности эффектом проскальзывания.

СЛУЧАЙ РЕАКЦИЙ 2-ГО ПОРЯДКА

Аналогично системе (6) модель микрореактора для реакции 2-го порядка имеет вид:

dF    ( F )

— = exp ------ d x       x^p + у • F

V           7

• в X

x [Da ₊ • G 1 • G 3 - Da - • G 3 ] • x^p ,

d G_i d x

^- exp

—F— x^p + Y • F ^{V 1 7}

X

x [Da ₊ • G 1 • G 3 + Da _ • G 3 ] x

Здесь i = 1, 2, 3; 1 — проба, 2 — реагент, 3 — продукт; индексы + и – относятся соответственно к прямой и обратной реакциям.

Граничные условия соответствуют разогреву холодной смеси в ходе химической реакции: F (0) = 0; G 1,2 (0) =1; G 3 (0) =0.

Результаты расчета представлены на рис. 4–6. Обозначения: U ^ 1 ^ — расстояние ( x ) вдоль оси капилляра; U ^ ^2> — изменение массового расхода пробы ( G 1 ) и реагента ( G 2 ) вдоль оси капилляра; U ^ — изменение потока теплосодержания ( F ) вдоль оси капилляра; U ^ 4 ^ — изменение массового расхода продукта ( G 3 ) вдоль оси капилляра (все величины безразмерные).

На рис. 4 показано влияние реологического фактора (обострение фронта пробы) при значительной скорости распада продукта.

На рис. 5, а показано, что сильное влияние реологии приводит к цикличности процесса и вполне возможной бифуркации при значительной скорости обратной реакции.

На рис. 6, б показано, что если скорости протекания химических реакций уменьшаются, то фактор реологии не в состоянии компенсировать это уменьшение и фронт пробы "размазывается", то есть уменьшается точность измерений.

Для применения этой модели в практических целях можно использовать время пребывания пробы в микрореакторе:

x x^p • ( - 1)\

t =

u m ( x ) = x ^p , 8 ( x ) = x^p .

*

^x d x _,

₀ u m

x ^* — расстояние по оси капилляра, где глубина превращения равна 0.95.

Если сравнить данное выражение для времени с аналогичными выражениями для времени при использовании методов:

ЭИА — t1 = L/(u1 + u3)                      (9)

и

ЭММА — t2 = L/(u3 - u1) ,                     (10)

то, поскольку величина u m может изменяться в зависимости от параметров процесса и физикохимических характеристик материалов пробы, реагента, буфера, всегда можно подобрать t = t 1 или t = t 2. То есть данная струйная модель включает в себя эти два подхода. Можно отметить, что эти два метода анализа по существу используют модель реактора вытеснения, которая предполагает смешение только посредством диффузии, что обычно существенным образом сказывается на длине реактора в сторону увеличения. Наша модель СМР учитывает как диффузию, так и эжек-цию.

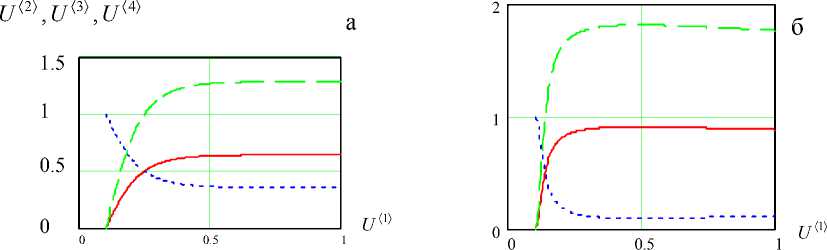
Рис. 4. Изменение вдоль оси параметров СМР:

а — β = 2, Da 1 = 5, γ = 0.3, Da 2 = 1, α = 0;

б — β = 2, Da 1 = 5, γ = 0.3, Da 2 = 1, α = 1;

_U 〈 2 〉 _{,                       U} 〈 3 〉 _{,                       U} 〈 4 〉

_U 〈 2 〉 _{, U} 〈 3 〉 _{, U} 〈 4 〉                _{а                                               б}

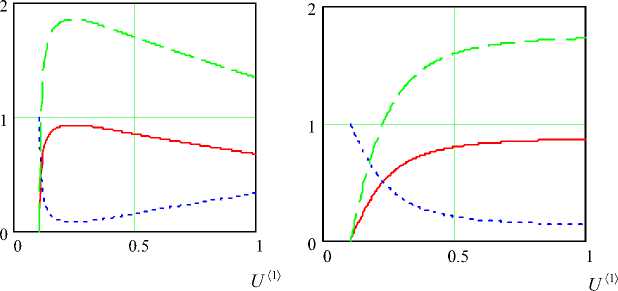
Рис. 5. Изменение вдоль оси параметров СМР:

а — β = 2, Da 1 = 5, γ = 0.3, Da 2 = 1, α = 2.5;

б — β = 2, Da 1 = 5, γ = 0.3, Da 2 = 0.1, α = 0;

в — β = 2, Da 1 = 10, γ = 0.3, Da 2 = 1, α = 0;

_U 〈 2 〉 _{,                       U} 〈 3 〉 _{,                       U} 〈 4 〉

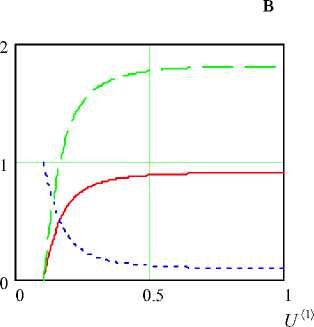
_U 〈 2 〉 _{, U} 〈 3 〉 _{, U} 〈 4 〉

а

б

0.5

_U 〈 1 〉

0.5

_U 〈 1 〉

Рис. 6. Изменение вдоль оси параметров СМР: а — β = 2, Da₁ = 5, γ = 0.3, Da₂ = 0.1, α = 2.5; б — β = 2, Da 1 = 4, γ = 0.3, Da 2 = 0.1, α = –2;

_U 〈 2 〉 _{,                       U} 〈 3 〉

_U 〈 4 〉

ЗАКЛЮЧЕНИЕ

№ 1. С. 40–44.

В данной работе построена модель струйного 2. Papautsky I., Ameal T., Frazier B. Review of

микрореактора и показана возможность с помощью выбора гидродинамических режимов создания требуемой формы фронта пробы с его локализацией в капилляре. Конкретное применение

данного подхода связано с оценкой времени пребывания пробы в микрореакторе в зависимости от его геометрии, физических свойств пробы, продукта, буфера и способа перемещения в микрореакторе.