Структура комплекса экономико-математических моделей межбюджетного регулирования

Для любой страны устойчивость финансового состояния является целевой установкой всей её хозяйственной деятельности. Поддержание состояния устойчивости требует от представителей управленческого персонала в сфере финансов ответственного отношения в процессе принятия решений, высокой квалификации и профессионального исполнения. Вопросы экономической стабильности Российской Федерации получили особую актуальность в условиях флуктуаций внешней среды, когда политикоэкономические санкционные воздействия привели к ограничительным политическим и экономическим мерам по отношению к Российской Федерации и ряду её институциональных единиц. Эти воздействия вызвали к 2016 году значительное сокращение темпов роста ВВП (Таблица1,

Таблица 1

Темпы роста ВВП России, %

год	значение
2007	8.5
2008	5.2
2009	-7.8
2010	4.3
2011	4.3
2012	3.4
2013	1.3
2014	0.7
2015	-3.7
2016	-0.8

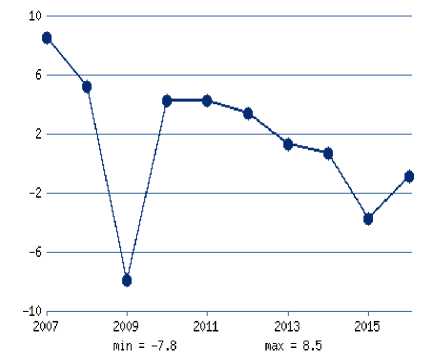
Рис.1. График темпов роста ВВП РФ в течение 2007-20015 г.

Приведённые данные демонстрируют, что к 2915 году темп роста ВВП Российской федерации снизился на 3,7 %. Если сравнить сложившуюся российскую экономическую ситуацию с положением других стран, например Америки (Таблица 2., рисунок 2) или Китая (Таблица 3., рисунок 3), то можно сделать вывод, что российская экономика переживает ситуацию стагнации, в которой меры государства становятся безотлагательными.

Таблица 2

Темпы роста ВВП США, %

год	значение
2007	1.9
2008	-0.3
2009	-3.5
2010	2.4
2011	1.8
2012	2.3
2013	1.5
2014	2.4
2015	2.6
2016	1.6

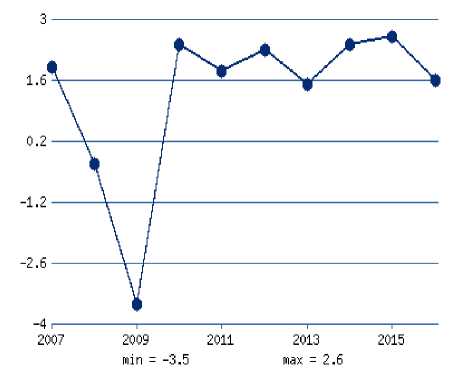
Рис.2. График темпов роста экономики США

Таблица 3

Темпы роста ВВП Китая, %

год	значение
2007	14.2
2008	9.6
2009	9.2
2010	10.4
2011	9.3
2012	7.7
2013	7.7
2014	7.3
2015	6.9
2016	6.6

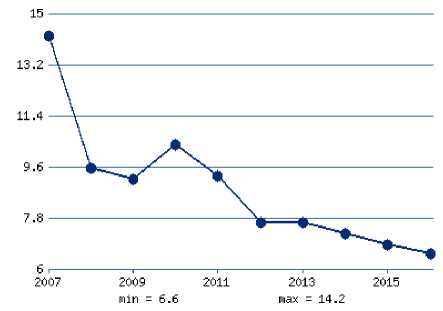
Рис.3. График темпов роста экономики Китая

В экономике США снижение темпов роста ВВП наблюдалось в 2008 и 2009 годах (соответственно -0,3% и – 3,55%), в то время как экономика Китая развивается высокими темпами. В 2015 и 2016 годах темпы роста ВВП Китая составляли соответственно 6,9% и 6,6 %, хотя по сравнению с 2007 годом эти цифры демонстрируют некоторое падение. Сравним

Сравним состояние Российской экономики с положением в таких странах СНГ, как Украина (Таблица 4, рисунок 4) и Белоруси (Таблица 5, рисунок 5).

Таблица 5

Темпы роста ВВП Украины, %

год	значение
2007	7.5
2008	1.9
2009	-14.5
2010	4.1
2011	5.2
2012	0.3
2013	0.0
2014	-6.6
2015	-9.9
2016	1.5

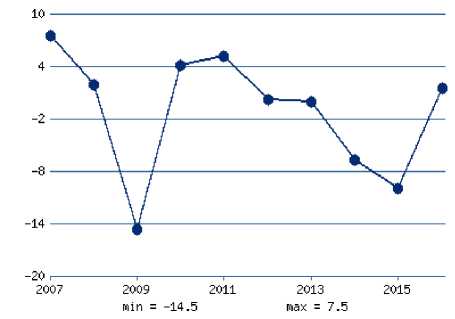
Рис. 5 График темпов роста экономики Украины

Таблица 6

Темпы роста ВВП Беларуси, %

год	значение
2007	8.6
2008	10.2
2009	0.2
2010	7.7
2011	5.5
2012	1.7
2013	1.0
2014	1.7
2015	-3.9
2016	-3.0

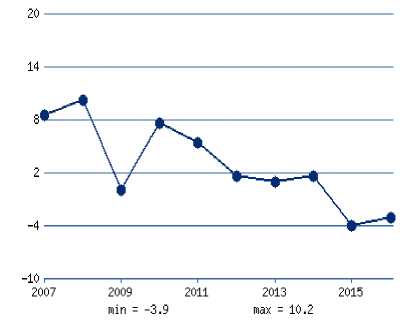
Рис. 6. График темпов роста экономики Белоруси

Рисунок 5 демонстрируют, что темпы роста ВВП в Украине в 2016 году превосходят российские. Что касается такой страны СНГ, как Белорусь, то спад её экономики является более масштабным, чем в России. Таким образом процессы, происходящие в экономике России, не могут не отразиться на экономических показателях развития ближайших стран СНГ.

Проводя анализ состояния российской экономики и разрабатывая мероприятия её дальнейшего развития, следует констатировать, что в сложившейся ситуации как никогда являются актуальными вопросы отказа от сырьевой ориентации и перехода к экономике инновационной, реализуя механизмы импортозамещения. В решении этих механизмов ведущую роль должно играть государство на основе использования набора эффективных инструментов управления макроэкономикой страны, среди которых особая роль принадлежит фискальной политике, позволяющей с помощью перераспределения финансовых ресурсов в системе административнотерриториального устройства порождать мотивы властей на местах к активизации инновационной и инвестиционной деятельности. К числу эффективных инструментов финансовой политики относится межбюджетное регулирование, позволяющее наряду с выравниванием уровня бюджетной обеспеченности административно-территориальных образований стимулировать территориальные властные структуры к наращиванию налогового потенциала. В отношениях межбюджетного регулирования стимулирующую функцию выполняет долевое распределение налоговых доходов между бюджетами по нормативам, определяемым властными структурами территорий вышестоящего уровня административнотерриториального деления Российской Федерации. Если рассматривать систему «регион-муниципальное образование», то величина этих нормативов устанавливается представителями государственной власти субфедерации и управленческим персоналом регионального Министерства финансов. В решении задачи реализации стимулирующей функции межбюджетного регулирования не решены вопросы оптимального распределения налоговых доходов между бюджетами по вертикали. Проводимые в настоящее время мероприятия по совершенствованию межбюджетных отношений не устраняют проблему концентрации налоговых поступлений в федеральных и региональных бюджетах. В результате задачи, стоящие перед муниципальными образованиями, оказываются недофинансированными, не говоря уже о финансовом обеспечении различного рода инноваций и др. Всё это приводит к встречным финансовым потокам в виде финансовой помощи. Таким образом, механизм совершенствования межбюджетного регулирования испытывает острую необходимость в разработке и использовании адекватного экономико-математического инструментария, позволяющего на формализованной основе определять пропорции распределения налогов в бюджетной системе Российской федерации с возможностью количественной оценки этих решений. Автором статьи предлагается структура комплекса экономико-математических моделей для реализации стимулирующей функции межбюджетного регулирования, приведённая на рисунке 7. В состав комплекса экономико-математических моделей включены: автоматная модель, обладающая целесообразным поведением, и имитационная модель.

База данных (накопление";

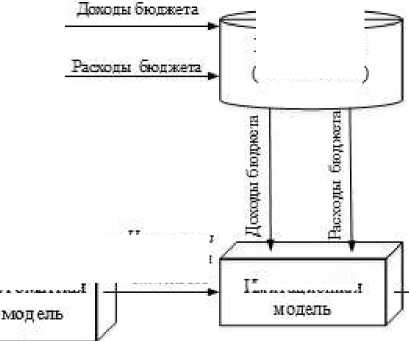
Имитационная

Зотиг (ЖХЬй-'еПКЫГ средспв

-Автоматная

Нфчкпмтезы

СЖГОМСТвИМЯ

ОП11НГПО306

Рис.7. Структура комплекса экономико-математических моделей

Исходными данными имитационной модели является статистическая информация о текущих доходах и расходах бюджета, поступающая из базы

данных, на основе которой строятся законы распределения вероятностей соответствующих случайных величин. В числе доходов рассматриваются следующие случайные величины: X_r - налоговые доходы, собираемые на территории муниципального образования, но предназначенные для зачисления в субфедеральный бюджет (по этим налогам устанавливаются нормативы отчислений в процессе межбюджетного регулирования); X_N -поступающие в местный бюджет неналоговые доходы; X_N - местные налоги; R — расходы местного бюджета. Законы распределения перечисленных величин, изменение которых носит вероятностный характер, представляют собой таблицы (Талица 7, Таблица 8, таблица9, таблица 10) .

Таблица 2.2

Распределение вероятностей случайной величины X_r

Середины интервалов	~1 A x r	~п A x r		A nX r
Относительные частоты	Ver	Verxr	• • •	Ver n

Таблица 2.3

Распределение вероятностей случайной величины X

Середины интервалов	~ A Xn	~ A Xn		A nXN
Относительные частоты	Ver ' XN	Ver 2 XN	• • •	Ver n XN

Таблица 2.4.

Распределение вероятностей случайной величины X

Середины интервалов	~ A X n	~ A X n	•'	A nX N
Относительные частоты	Ver 1 XN	Ver 2 XN		Ver n XN

Таблица 2.5

Распределение вероятностей случайной величины R

Середины интервалов	А ' R	А 2 R	• —.	А nR
Относительные частоты	Ver R	VerR		Ver R

Ячейки первой строки приведённых таблиц заполнены величинами середин интервалов отрезков, на которые разделены размахи варьирования случайных величин. Ячейки второй строки содержат относительные частоты попадания случайных величин в заданные отрезки [1,2,3]. Для определения занесённых в таблицы данных вычисляется размах варьирования случайных величин, как:

А _у = max у - min у ; А— = max — - min— ;

Xr          Xr         Xr     Xr          Xr

А у = max у - min _у ; А „ = max _у - min _у .

XN        XN       XN   R        XRX

В последних выражениях величины max^ ,min;r , max —, min —, r          r         Xr max x , min x, max Xr , min Xr представляют собой соответственно максимальные и минимальные значения случайных величин Xr, X N , XN, R, вычисленные по введённым из базы данных статистическим данным. Величины декомпозированных интервалов, на которые разбиваются Ах ,

А—, А_хn , А_к , определяются по формулам: