Структура нелинейных вистлеров, движущихся в плазме под углом к магнитному полю

В данной работе рассматриваются установившиеся нелинейные волны — вистлеры, распространяющиеся под некоторым углом α (α≠π/2) к постоянному однородному магнитному полю в холодной бесстолкновительной плазме. Основное внимание акцентируется на волнах типа быстрого магнитного звука (БМЗ), которые при выполнении условия ωHе<<ωpе имеют частоты ωHi<<ω<ωHеcosα и длины волн порядка электронной инерционной длины с/ωpе (здесь ωHi — ионная циклотронная, ωHе — электронная циклотронная, ωpе — электронная плазменная частоты, с — скорость света). БМЗ-волны в этом диапазоне частот имеют несколько названий: свистящие атмосферики, свисты, геликоны, вистлеры [Ахиезер и др., 1974; Гершман, Угаров, 1960]. Мы будем называть эти волны вистлерами. Вистлеры наблюдаются достаточно часто во многих явлениях, имеющих место в замагниченной космической плазме. К примеру, вистлеры, возбуждаясь в околоземной плазме вследствие непрерывных грозовых разрядов в атмосфере Земли [Гершман, Угаров, 1960], постоянно регистрируются радиоприемниками на Земле. Другой пример — в последнее время установлено, что вистлеры играют существенную роль в формировании структуры бесстолкновительных ударных волн [Balogh, Treumann, 2013], в частности, это относится и к околоземным ударным волнам [Wilson III, 2016].

Как следует из результатов работы [Saffman, 1961] , для установившихся нелинейных вистлеров, бегущих строго вдоль силовых линий внешнего магнитного поля, волновое магнитное поле имеет две сравнимые по величине, поперечные к направлению движения волны компоненты, а вектор волнового магнитного поля вращается в той же поперечной плоскости. Характерный пространственный масштаб вистлера порядка ~ c /ω pе . Скорость вистлера, бегущего строго вдоль внешнего магнитного поля, на порядок величины превышает альфвенов-скую скорость в невозмущенной плазме, а амплитуда поперечных компонент волнового магнитного поля вистлера при максимальных его скоростях на порядок величины превышает значение внешнего магнитного поля. Как показано в представленном исследовании, похожую структуру имеют вистлеры, бегущие под углом к магнитному полю.

ПОСТАНОВКА ЗАДАЧИ И ИСХОДНЫЕ УРАВНЕНИЯ

Рассмотрим задачу о структуре нелинейного возмущения в замагниченной холодной плазме, которое движется со скоростью U 0 под углом α к внешнему стационарному магнитному полю величиной

Н_В . Все рассмотрение будем вести в системе отсчета, связанной с волной возмущения. Предположим, что движение частиц плазмы является нерелятивистским. Ограничимся одномерным случаем, т. е. будем полагать, что все переменные величины зависят только от координаты х . Кроме того, предположим, что в невозмущенной волной плазме внешнее однородное магнитное поле имеет компоненты Н х 0 =H В cosα и Н z 0 =H В sinα. В приближении двухжидкостной магнитной гидродинамики, полагая, что при выполнении условия ω Hе <<ω pе плазма квазинейтральна, и можно пренебречь эффектами, связанными с конечным давлением фоновой плазмы, получим для установившихся волн в водородной плазме следующие соотношения [Карпман, 1973; Tidman, Krаll, 1971; Сагдеев, 1964; Kellogg, 1964; Aldam, Allen, 1958] :

m p Ud v p / dx = e E + e [ v p × H] / c , m e Ud v e / dx =– e E – e [ v e × H] / c ,

V x H = 4nen (vp - ve) / c, V x E = 0, ne(x)=np(x)=n(x), Up(x)=Ue(x)=U(x), n(x) U(x)=сonst=j,

Н_х=сonst=H_{х 0} ≡H ₀, Е_у=сonst ,

Е z =сonst , Е х =–[1/( mc )][( m е v p +m p v e )× H ] x .

Здесь Е , Н — векторы электрического и магнитного полей, U — х- компонента скорости частиц плазмы, n — плотность частиц, v p , m p — вектор скорости и масса протонов, v e , m е — вектор скорости и масса электронов, е — заряд электрона, m=m p +m e . Из приведенных выше соотношений имеем следующие законы сохранения импульсов:

mU+(Ну2+Нz2)/(8πj)=р, mpVp+meVe–Н0Ну/(4πj)=р1, mpWp+me We–Н0Нz/(4πj) =р2, где р, р1, р2 — константы, а через V и W обозначены у- и z-компоненты скорости частиц соответственно. Задавая значения переменных в невозмущенной плазме (х→ –∞)

H_у =0, H_z = H_{z 0}, d H / dx =0, Е_х = Е_z =0,

Еу=U0Hz0/с, U=U0, n=n0, Vp=Ve=Wp=We=0, получим для констант значения р=mU0+Нz02/(8πj), р1=0, р2=–Н0Нz0/(4πj).

Введем безразмерные переменные и параметры. Координату нормируем на длину c/ωp и обозначим как ξ=хωp/c, где top = ^4nn0e2 m I (me mp) ® tope, безразмерное время обозначим как

τ=ωgt, где tog = eHB I (c^memp). Безразмерные величины компонент магнитного поля, нормированные на величину НВ, обозначим как h (с соответствующим индексом), х-, y- и z-компоненты скоростей частиц, нормированные на величину VA, обозначим как u, v и w соответственно (здесь VA = HВ I ^4nn0m — скорость альфвеновских волн в невозмущенной

Structure of nonlinear whistlers moving through plasma… плазме). Безразмерный потенциал обозначим как ψ = 2 e φ/( mU ₀²). Используем следующие обозначения для безразмерных параметров: альфвеновское число Маха М=U ₀/ V _A, h ₀= H ₀ /H_В= cosα, корень из отношения масс частиц ц = ^ m _p I m e , R= ц+1/ц.

Учитывая, что u=d ξ /d τ, из вышеприведенных соотношений получим систему уравнений для нахождения безразмерных компонент скоростей частиц и компонент магнитного поля в волне возмущения:

dve/dτ=μ(uhz–Mhz0–weh0),(1)

dwe/dτ=μ(veh0–uhy),(2)

dhy/dτ=[h0(hz–hz0)–Мwe]/μ,(3)

dhz/dτ=(Mve–h0hy)/μ,(4)

u=M+(hz02–hy2–hz2)/(2M),(5)

vp=–ve/μ+(1+μ–2)h0hy/M,(6)

wp=–we/μ+(1+μ–2)h0(hz–hz0)/M.(7)

Система уравнений (1)–(4) с учетом (5) достаточна для того, чтобы найти компоненты магнитного поля и компоненты скорости электронов. Уравнения (6)–(7) позволяют найти компоненты скорости протонов.

Систему уравнений (1)–(7) можно решить, используя численные методы решения систем дифференциальных уравнений. Для ее решения был использован метод Рунге—Кутты. Проводилась тщательная проверка точности полученных численных решений путем сравнения их с аналитическими формулами для двух частных случаев: 1) волна, бегущая строго вдоль (α=0) внешнего магнитного поля [Saffman, 1961]; 2) волна, бегущая строго поперек (α=π/2) внешнего магнитного поля [Aldam, Allen, 1958] . Сравнение показало, что точность вычислений была не хуже 10^–5.

ПРИБЛИЖЕННЫЕ

АНАЛИТИЧЕСКИЕ РЕШЕНИЯ СИСТЕМЫ УРАВНЕНИЙ (1)–(7 )

Учитывая результаты работы [Saffman, 1961] , можно предположить, что для косых БМЗ-волн, бегущих с максимально возможной скоростью почти вдоль внешнего поля ( h_{z 0}<<1 , h ₀≈1), амплитуда поперечных компонент волнового магнитного поля в десятки раз превосходит величину внешнего поля H_В . Используя этот факт, в нулевом приближении можно пренебречь вкладом в суммарное поле поперечной компоненты внешнего поля h z 0 и в качестве граничного условия (при х→ – ∞ ) положить h z 0 =0. При таком упрощении система уравнений (1)–(7) имеет аналитическое решение. Действительно, полагая h z 0 =0, из системы (1)–(7) получим следующие соотношения:

w e ² +v e ²=μ²( M ²– u ²), w p ² +v p ²=( M ²– u ²)/μ², w e h y – v e h z = – μ²( w p h y –v p h z )=

=μM(wevp–wpve)/(Rh0)=μdu/dτ, (wevр–wрvу)2+(vevр+wewр)2= =(we2+ve2)(wp2+vp2)=(M2–u2)2, которые можно свести к одному дифференциальному уравнению для переменной u:

du / d т=( M - u )[4 M ²- h o ² R ²-2 M ( M - u )]^1/2.

Отсюда, с учетом граничных условий, после интегрирования получим u=M-2Х2sech2( Хт)/ M,                     (8)

b = Jh2 + hZ = 2X s ech (Xt) , где Х=^M^-h^^p+^^^^^TZ. Отличие от решения [Saffman, 1961] состоит в том, что параметр Х зависит от h0=cosa. При h0=cosa =1 формулы (8)-(9) совпадают с формулами, полученными в работе [Saffman, 1961]. Так же, как и в [Saffman, 1961], в данном решении для каждого заданного угла a число Маха волны имеет ограниченный интервал возможных значений:

( ц + 1/ ц ) cos a /2 <  M <  ( ц + 1/ ц ) cos a / 41.

Компоненты поля через его модуль b представим в виде hz=bcose, hy=bsine.

Аргумент в найдем, учитывая формулы (1)-(4): в=в(т)=(р2-1)h0/(2р)т. Таким образом, окончательные формулы для компонент магнитного поля hz=2 Х cosвsech( Хт),                         (9)

hy=2 Хsinвsech( Хт), где в=в (т )=( р2 — 1) h o/(2 р) т=Yт ( у=h o( р -1/ р )/2). Используя эти формулы, из уравнений (3)-(4) получим выражения для поперечных компонент скоростей электронов, а из (6)-(7) — для поперечных компонент скоростей ионов. Остается найти профиль потенциала вистлера, для чего используем формулу dф/dx =[1/(mc)][(mеvр+mрve)xH]x. В безразмерном виде эта формула примет вид с (d ф / dx)/(Н Va)=mM2( d у / d ^)/[2( m е m p)1/2] = =( m е/m)(v р hz-w р hy)+(m р/m)(ve hz-w ehy).

Используя здесь соотношения v р hz-w р h y=-( m e/m р)( v e hz-w e hy )=

=-(m e/m р)1/2 u (du / d £), получим d у / d^=-[(р2 -1)/( р 2+1)][ d (u2/M2)/d ^].

Учитывая граничные условия и полагая, что р²>>1, имеем у = 1- u ²/ M ². Нетрудно видеть, что потенциал вистлера максимален у=у _m , а х- компонента скорости частиц минимальна u =0 при т = 0:

у _m=у (0)=1 - (1-2Х²/ М ²)²=4(1- Х²/ М²) Х²/ М ²

=( h 0 ² R ²/ М ²)[1- h 0 ² R ²/(4 М ²)].

Максимальное значение потенциала равно нулю при минимальном числе Маха M = h ₀ R /2 и имеет предельное значение у = 1 при максимальном числе Маха M = h ₀ R / V2. Следует отметить интересную особенность полученных нами результатов: минимальная скорость распространения рассматриваемых нелинейных вистлеров, амплитуды компонент магнитного поля и потенциала которых бесконечно малы, равна максимальной фазовой скорости, которую в линейном приближении имеют БМЗ-волны с длинами волн порядка с /ю_ре.

В завершение наших расчетов из (8) получим формулу, устанавливающую связь между координатой ^ и временем т:

^( т )= M т - 2 Х th (Хт)/ M .

С учетом этой формулы соотношения для потенциала, компонент магнитного поля и скоростей частиц плазмы полностью определяют структуру вистлеров. На рис. 1-3 представлены пространственные профили компонент магнитного поля и потенциала для двух значений чисел Маха, одно из которых, М= 27.56, близко к максимальному значению, другое, М= 22.44, — к минимальному. Как видно из этих рисунков, при уменьшении числа Маха изменяется пространственная структура профилей потенциала и компонент магнитного поля, а амплитуда как компонент магнитного поля, так и потенциала уменьшается. Пространственный профиль потенциала (рис. 3) имеет форму уединенной волны, или солитона. Аналогичную форму имеют профиль потенциала для ионнозвукового солитона [Ахиезер и др., 1974; Сагдеев, 1964] и профили потенциала и магнит-

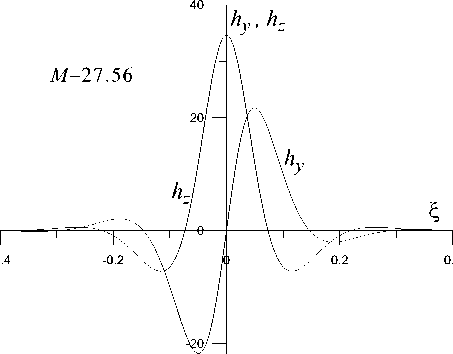
-40

Рис. 1. Профили компонент магнитного поля вистлера h_y , h_z для числа Маха М= 27.56

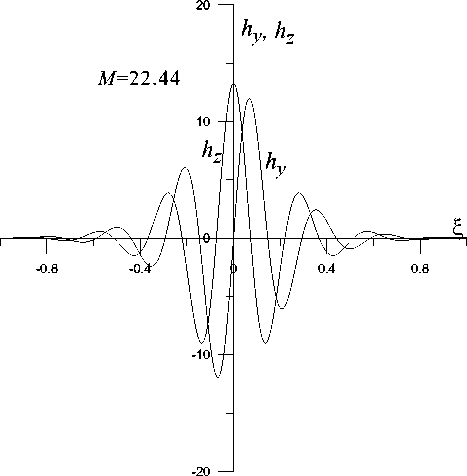
Рис. 2. Профили компонент магнитного поля вистлера h_y , h_z для числа Маха М= 22.44

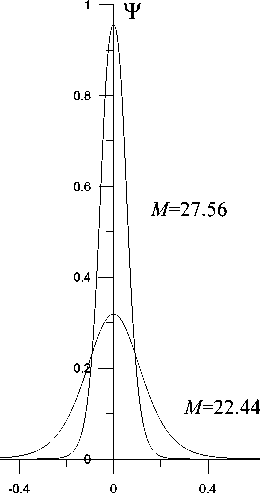
Рис. 3 . Пространственные профили потенциала вистлера для чисел Маха М= 27.56 и М= 22.44

ξ

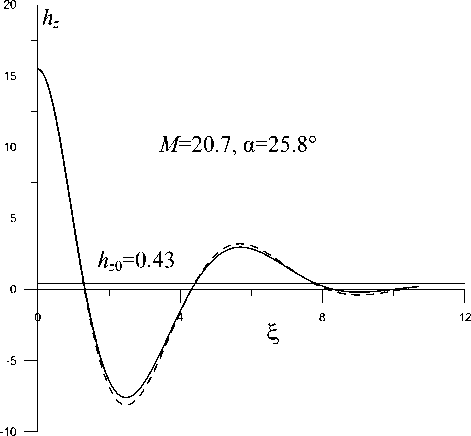
Рис. 4 . Пространственные профили компоненты h_z , полученные из численных расчетов (сплошная линия) и рассчитанные по формуле (9) (штриховая линия) для параметров М= 20.7, h 0 =0.9, h z 0 =0.43

По нашему мнению, полученные нелинейные решения для вистлеров определяют нелинейную структуру ударного разрыва сверхкритических косых бесстолкновительных ударных волн (БУВ), на фронте которых наблюдаются скачки магнитного поля достаточно большой амплитуды [Balogh, Treumann, 2013] . Речь идет о БУВ, распространяющихся в космической плазме, в частности, это касается межпланетных и околоземных БУВ. Предполагается, что пространственная структура скачка магнитного поля на фронте БУВ имеет форму нелинейного вистлера. Это предположение подтверждается численным экспериментом, изложенным в работе [Krasnoselskikh et al., 2002] . Авторы работы [Krasno-selskikh et al., 2002] особо подчеркивают существенную роль, которую играют нелинейные вистлеры в формировании фронта сильных БУВ.

ОСНОВНЫЕ РЕЗУЛЬТАТЫ И ВЫВОДЫ

• 1.    Получены решения уравнений двухжидкостной гидродинамики, описывающие мелкомасштабные быстрые магнитозвуковые нелинейные волны — вистлеры, движущиеся в плазме под углом α к внешнему магнитному полю.

• 2.    При фиксированном угле α альфвеновское число Маха М вистлеров имеет небольшой интервал разрешенных значений: µ cos α /2 < M < µ cos α / 2. При переходе от предельно малых чисел Маха к предельно большим амплитуда и пространственная структура потенциала волновых компонент скорости и магнитного поля вистлера существенно изменяются.

• 3.    Определен диапазон углов направления движения вистлеров по отношению к направлению вектора внешнего магнитного поля, в пределах которого полученные приближенные аналитические и численные решения удовлетворительно согласуются. Для скоростей вистлеров, близких к предельно большим значениям M ≈ µ cos α / 2 , — это интервал углов 0°<α<80°.

Работа выполнена в рамках проекта II.16.1.3. программы фундаментальных научных исследований СО РАН II.16.1 по приоритетному направлению II.16.

ного поля для строго поперечного магнитозвукового солитона [Ахиезер и др., 1974; Карпман, 1973; Tid-man, Krаll, 1971; Сагдеев, 1964; Aldam, Allen, 1958] .

Для определения границ применимости наши приближенные решения сравнивались с решениями, следующими из численных расчетов. Результаты такого сравнения приведены на рис. 4, на котором отображена только половина симметричного относительно точки ξ=0 профиля компоненты h z . Наилучшее согласие наблюдается для чисел Маха, близких к предельно большим значениям, для которых сравнение позволило нам установить область применимости нашего приближения — это интервал углов 0°<α<80°(1> h 0 >0.2). В найденном интервале аналитические решения вполне пригодны для описания структуры магнитного поля в косых вистлерах.