Структура плоских волн для частицы со спином 3/2, безмассовый случай, калибровочная симметрия

После работ Паули–Фирца [1, 2] и Рариты– Швингера [3] в физической литературе всегда присутствовал интерес к теории частиц с высшими спинами, в том числе и к частице со спином 3/2 [3– 20]. Для описания частицы со спином 3/2 требуется 16-компонентная волновая функция с трансформационными свойствами вектор-биспинора относительно группы Лоренца. В литературе наибольшее внимание привлекло существование аномальных решений для массивной частицы в присутствии внешних полей, которым сопоставляется скорость частицы большая, чем скорость света. Отдельный интерес представляет случай безмассовой частицы со спином 3/2. Как показали Паули и Фирц [1], здесь существует специфическая калибровочная симметрия, выражающаяся в том, что 4-градиент от произвольной биспинорной функции дает решения безмассо-вого волнового уравнения, т. е. в безмассовом случае среди множества решений волнового уравнения всегда присутствуют четыре калибровочные решения, которые являются физически ненаблюдаемыми, по- скольку, например, не дают вклада в тензор энергии-импульса частицы. В данной работе мы проследим за степенями свободы безмассовой частицы со спином 3/2 на основе построения в явном виде решений типа плоских волн, и найдем решения, которые не содержат калибровочных компонент.

1. Безмассовая частица

Система уравнений первого порядка для без-массовой частицы в базисе Рариты–Швингера имеет вид [16]

d a Y a Ф k - 3 d k Y ‘ Ф i - 3 Y k d a Ф a +

+ 3 Y k ( Y a d a ) Y l Ф i = 0 , d a (Г a ) k Ф i = 0 ,   (1)

где действующие в 16-мерном пространстве волновой функции матрицы задаются соотношением a\i     a.axl 1 ixa 1    „al     1 „,a„,l

^(r ) k = Y O k - 3 Y O k - 3 Y k g ⁺ 3 Y k Y Y . (2)

биспинорные индексы у матрицы Г ^a опускаем. Ниже будем использовать известные свойства матриц Дирака [17]:

Y a Y b + Y b Y a = - g ab , Y a Y a = 4 ,

Y a Y ^b Y d = Y a g bd - Y b g ad + Y d g ab - -Y 5 e abdc Y c ; (3)

в спинорном базисе имеем

Y '⁵ = ₊ ,y ⁰ y ¹ y ² y ³ = ( 0 -I ) . = ⁰¹²³ = +1

Если воспользоваться формулой для произведения трех матриц Дирака, то для матриц (Г a ) k можно получить другое представление:

(Г a ) k = 3 Y a O k — 3 Y ⁵ -a         d a (Г a ) k Ф i = 0 . (4)

Совершим над уравнением [1] последовательно два преобразования. Сначала умножим его слева на невырожденную матрицу C со структурой C n = O k + cY n Y ^k , в результате получаем другие матрицы (Г ‘ a ) П :

(Г ‘a) П = YaSln — 3 Yl 6П + 2c—1 Yngal + 3 YnYaYl, da (Г‘a )П Фi = 0.                  (5)

Отсюда, воспользовавшись формулой для умножения трех матриц Дирака, получим

‘a\i      ²,a c i i ² c„, „ai     i „ ,5 alk^,

^(Г ) n = 3 Y ^S n ⁺ -3- Y n g ^- 3 Y O n Y k ;    (6)

т. е. уравнение (1) приводится к виду

3 d a Y a Ф n + -^Yn d a ф a — -Y ⁵ ■ k d a Y k Ф i = 0; (7)

параметр c пока не фиксирован. Затем в ур авнении (7) перейдем к новой волновой функции Ф с помощью матрицы S :

Ф = S Ф , Sd a Г ‘ ^a S ^- 1 Ф = 0 , s m = s m + aY m Y n , ( S — ¹ ) k = s + bY i Y k , SS ^{- 1} = I = ^ a + b + 4 ab =1 .      (8)

В результате находим новое представление для матриц уравнения

ak ak _m γ _m

+ Y ^k s m[

-

-

-

b ^{- c}

-

— (1+4 a )+- a +3 +

-

1₊1+- b + b

3 3 3

- c + Y m g ^ak

-

Г - c — 1,      x        1П

[ 3      ⁴ a ⁾⁺² a ⁺3jr

— (1 + 4 k ) + - a + 3 +

- c- 1„             1Ц

⁺ b I —3—^{(1 + 4} a )^{+ -} a ⁺ 311 ^-

3⁺ b

- c - 1

(1 + 4 a ) + a +

_iγ 5 _ϵ a_mkn _{γ n .}

Потребуем, чтобы в (9) осталось только слагаемое, содержащее символ Леви–Чивита. Это дает три уравнения на параметры a, b, c (помним об условии a + b + 4 ab = 0 ):

3 = —3—^{(1 + 4 a} ) ^{b + - ab +} 3 .

• ^- "! + {^- cT ¹ (1 + 4 a ) b + - ab + 3} =0 ’

• — 3—^{(1 + 4} a )^{+ -} a ⁺ 3+

• - c - 1                    b

+ ^ —3—(1 + 4 a ) b + - ab + 3 г = 0 .

Их решение следующее:

Ф = S^, a = - 3 , b = - 1 , c = - ,

C k = s n +- Y n Y ^k , S n = s n - 3 Y n Y ^k , ( S — 1 ) n = O n - Y n Y k .

Следовательно, уравнение для безмассового поля со спином 3/2 в этом базисе имеет вид da (Г) m Ф k = 0, -da [ iY5 omknYn ]Ф k = 0.   (12)

Очевидно, что вектор-биспинор в виде градиента от произвольного биспинора Ф( x )

Ф krrad ( x ) = d k ф( x )              (13)

всегда будет решением уравнения (12). Это свойство иначе называют калибровочной симметрией. В исходном базисе калибровочные решения представляются так:

Ф grad ( x ) = d i Ф - Y i Y ^k d i ф , l = 0 , 1 , - , 3 . (14)

Уравнение (12) можно записать в безиндекс-ной форме, если ввести шесть матриц:

nak       [ na ] k [ na ]         [ an ]

^ m ^{( Ц}   ) m , ^{Ц         Ц} ;

-iY 5 Y n d a ® Ц ^{[ па ]} Ф = 0 ,          (15)

где Ф - это (4 x 4) -матрица, ее первый индекс бис-пинорный, второй – векторный. Простота уравнения (15) обманчива, фактически имеем следующее:

( —i ) { Y 5 (Y 1 ® Ц ^[01] + Y 2 ® Ц ^[02] + Y 3 ® Ц ^[03] ) д 0 Ф+

+ Y 5 ( Y ⁰ ® Ц ^[01] + Y 2 ® Ц ^[12] — Y 3 ® Ц ^[31] ) д 1 Ф+

+ Y 5 ( Y ⁰ ® Ц ^[02] + Y 3 ® Ц ^[23] — Y 1 ® Ц ^[12] ) д 2 Ф+

+ Y 5 (Y ⁰ ® Ц ^[03] + Y 1 ® Ц ^[31] — Y 2 ® Ц [23] ) д зФ } = 0 .

Будем искать решения уравнения (16) в виде плоских волн, ориентированных вдоль оси x 3 (это не уменьшает общности рассмотрения, поскольку всегда можно выбрать систему координат так, чтобы удовлетворить условию к ⁰ = ( е, 0 , 0 , к )) :

[Ф an ] = -t e ikz Ф ,

	0	0	1	0	0	0	0	1
[31]	1 0	0	0	0 I [12]	1 0	0	0	0
Ц tr =	1	0	0	0   , Ц tr =	0	0	0	0
	0	0	0	0	1	0	0	0

Дальше находим 16 уравнений, которые разбиваются на четыре независимые системы:

f0 f1 f2 f3 Ф an — g0  g1 g2 g3 h0  h1 h2 h3 .          (17) d0 d1 d2 d3 дит к одному и тому же условию

I, 1	—ik k 0 0	—ie ϵ 0 0	0 - ( е + к ) ik —ie	- ( к + е ) \ 0 I —к I ϵ		d 0 d 3 h 1 h 2		= 0;
II,	/ ik 1 —к 0 0	iϵ —е 0 0	0 — ( е — к ) —ik iϵ	( е — к ) \ 0 I —к 1 ϵ	/ h 0 \ h 3 d 1 d 2			= 0;
III,	/ —ik 1 —к 0 0	—1е —е 0 0	0 ( е — к ) ik —ie	— ( е — к ) \ 0 I —к    I ϵ		/ g 0 I g 3 1 f 1 f 2		I = 0;
IV,	/ ik 1 —к 0 0	iϵ —е 0 0	0 — ( к + е ) —ik iϵ	( к + е ) \ 0 I —к I ϵ		f 0 \ f 3 g 1 g 2		= 0 .
Требование		равенства нулю		определителей				приво-

( к ² — е 2 ) 2 = 0 .                 (20)

С учетом подстановки (17) уравнение (16) упрощается

-6Y ⁵ ( Y 1 ® Ц ^[01] + Y 2 ® Ц ^[02] + Y 3 ® Ц ^[03] ) д 0 Ф+

+kY5(Y0 ® Ц[03] + Y 1 ® Ц[31] — Y2 ® Ц[23]) д3Ф = 0, кратко его можно записать так:

—eY ⁵ B 0 Ф + kY ⁵ B 3 Ф = 0 .         (19)

Ниже будем использовать матрицы Дирака в спинорном базисе [16]:

	0	0	10			0	0	0	— 1
Y 0 =	0 1	0 0	01 00	II ,	Y 1 = |	0 0	0 1	— 1 0	0 0	II ,
	0	1	00			1	0	0	0
	/ 0	0	0	i		/ 0	0		— 1	0 \
Y 2 =	1 0 1 0	0 —i	—i 0	0 I 0	, Y 3 =	1 0 1	0 0		0 0	1 I 0 ,
	i	0	0	0		0	— 1		0	0
также	потребуются выражения для						шести		(транспо-
нированных) матриц:
	/ 0	0	0	0 \			/ 0	0	0	0 \
[01] µ tr	0 0	0 0	0 0	0 1	I [02] , µ tr	= 1	0 0	0 0	0 0	— 1 0 ,
	0	0	— 1	0			0	1	0	0
	/ 0		00	0			/ 0	1	0	0 \
[03] µ tr	1 0 =0		01 10	0 0	I [23] , µ tr	=	1 0	0 0	0 0	0 I 0 ,
	0		00	0			0	0	0	0

Способ исследования уравнений такой: находим линейно независимые решения каждой подсистемы, при этом описываем только входящие в нее переменные, а остальные полагаем равными нулю; таким образом, находим все независимые решения исходной системы из 16 уравнений. Будем строить решения, предполагая е >  0 . Это означает, что исследуем случай частиц, для античастиц соответствующие решения можно получить с помощью операции зарядового сопряжения Ф C = ( y ² ® I )Ф * из строящихся ниже решений. Положительность энергии возможна в двух случаях: к >  0 , е = к и к <  0 , е = —к ; для определенности следим за вариантом к >  0 . Тогда приведенные выше уравнения упрощаются (сразу приводим их решения):

—i

I,

—i

1 0

— 2

—i

— 2 0

— 1 1

d 0 d 3 h 1 h 2

= 0;

d 0 - любое, d 3 = — d ₀ , h 1 = 0 , h 2 = 0;     (21a)

II,

i

— 1 0 0

i

— 1 0 0

0   0 \ A (A

0    0  I

—i  — 1 I i   1 /V2/

h 0 , d ₀ -любые, h 3 = —h ₀ , d 1 = id 2 ;       (21b)

( -i  -i   0   0 \ gg_ (A

-1  -1   0    0I

0    0     i   - 1     1 1 = ^0;

0   0  -i   1 у

_0J2-любые, _3 = -_0, 11 = if2;

i	i	0	2\ / 1 0\
IV, I 0	- 1 0	- 2 i	0 1 1 1 3 1 = 0 - 1     _ 1
0	0	i	1 / \_ 2/
f 0 – любое, f 3	=	-f 0 ,	_ 1 = 0 , _ 2 = 0 •	(21d)

Следовательно, общее решение системы уравнений имеет вид

f0 -if2 f2 -f0 ф = g0 h0 0 0 0 0 -g0 -h0 ;      (22a) d0 id2 d2 -d0 его можно разложить в суперпозицию шести независимых:

(10 0 0 -10\    ( 0 0 00

Ф    I 0 0 0    0  1,1 g0  00  -_0 I,

Ф =   0 0 0   0   +  0  0 0   0

\ 000  0 У  \ 0 0 00 у

/0 0 0      \    /0 0 00

0   0  0    0         0   0  00

+ I h0  0  0  -h0 I + I 0   0  0    0 I

\ 0  0  0   0 У     \d 0   0  0   —d 0 У

/0  -i12  12  0\    /0   0   00

,  I 0      0       0    0 I  ,  I 0    0     00

+ I 0     0      0   0 I + I 0    0    00

\0    0     0   0)    \0  id 2  d 2

(22b)

В свою очередь, калибровочные решения имеют вид (множитель e ^iϵt e ^ikz опускаем)

⁽ L 1 \

Ф K = -ie I L ² I ¥K = 0

^Ф 0            L 3 ’ ^Ф 1     ⁰ ’

L ₄

⁽ L 1 \

¥ K = 0 , ¥ K = ik I L 3 I ,         (23)

L 4

где L ₁ . . . L ₄ – произвольные числовые параметры. Для матрицы общего калибровочного решения имеем следующее представление (учитываем e = k >  0 , далее этот общий множитель опускаем)

ф K

-iL 1

I -iL 2

-iL 3

-iL 4

0 0 iL Д

0 0 iL 2 I

0 0 iL 3 ^•

0 0 iL 4У

Легко убедиться, что все независимые калибровочные решения удовлетворяют полученным выше уравнениям:

-i -i 0 -2 -iL4 I, 1 0 1 0 -2 i 0I -1 I+iL4 I 0 = 0; 0 0 -i 1 0 i i 0 0\ -iL3\ II, II -1 0 -1 0 0 -i 0 II -1 +iL3I 0 = 0; (25) 0 0 i 1 0 -i -i 0 0 /-iL2 III, I-1 0 -1 0 0 i 0 -1 I I+iL2 0 I = 0; 0 0 -i 1 0 i i 0 2\ /-iL1 IV, -1 0 -1 0 -2 -i 0 -1 I+iL1 0 I = 0 • 0 0 i 1 0 Также замечаем, что первые четыре решения в су- перпозиции (22b) являются чисто калибровочными

(см. (25)), поэтому они могут быть отброшены. Таким образом, в (22а) остаются только два независимых решения, они не содержат калибровочных ком- понент:

0  -i12  12  0\    /0   0   0Д

I0     0      0    0 I  ,  I 0    0     00

Ф I 0     0      0   0 I + I 0    0     00

\ 0   0    00)   \0 Id 2  d 2

Теперь исследуем эту задачу, используя исходный базис Рариты–Швингера (4). В матричной форме уравнение записывается так:

[3 d a Y a ® I - 3 y 5 d a Y n ® M an ] ф = 0 •    (27)

Для плоских волн уравнение принимает вид (см. (19))

- 2 ieY ⁰ Ф + 2 ikY ³ Ф - eY ⁵ B 0 Ф + kY ⁵ B 3 Ф = 0 • (28)

После необходимых вычислений находим 16 уравнений, группируем их в четыре несвязанные подсистемы:

/   -ik      -ie - 2 i ( e + к )

I, I       k         e - ( e + k )

\- 2i (e - k)0

II,

ik

-k

- 2 i ( e + k ) 0

• ^-    ( ^{k + e} ) \ ( d 0 \

• -    2 i ( e + k ) I I d 3 I =

• -kh

ϵh ie       -2i(e - k)

• -e       - ( e - k )

• - 2 i ( e + k ) ie

( e - k ) ^{\ /} h 0 ^\

• - 2 i ( e - k ) I I h 3 I ₌

• -kd

ϵd

IV,

—ik         —ie      — 2 i ( e — k )

—k          —e        ( e — k )

— 2 i ( e + k )       0             ik

0        — 2 i ( e + k )       —ie

^— ( ^{e —} к )

— 2 i (e — k )

-k ϵ

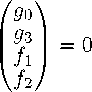
ik

iϵ

-k

— 2 i ( e — 0

k )

-ϵ

— 2 i ( e —

k )

— 2 i ( e + k ) ^{— (} к + ^e ) -ik iϵ

( k + e ) \ f 0 o\

^—2 i ^{( e} + к ) I I f 3 I =

—k II g 1 1 ϵ          g 2

Дальнейший анализ проводится по прежней схеме. Строим решения, предполагая e >  0 . Положительность энергии возможна в двух случаях: k >  0 , e = k и k <  0 , e = —k ; следим за вариантом k >  0 . Тогда системы упрощаются (общий множитель e = k опускаем)

I,

-i

1 0

-i

1 0

— 4 i

— 2

-i

— 2

— 4 i

— 1 1

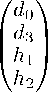
= 0;

h 0

h 3 I d 1 d 2

II,

i

— 1

— 4 i

i     0    0\

—1   0    0

0   —i—

—4i   i1

= 0;

III,

-i

— 1

— 4 i

-i

IV,

i

— 1 0

— 1 0 — 4 i

i

— 1 0

0 i -i

— 4 i — 2

-i i

— 4 i

— 1 1

Общее решение имеет вид

f 0        f 1 f 2

4 (fi+if2)0 0

4 (id2 — d 1)0 0

d0

— 1

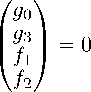
f 0 f 3

g 1

g 2

= 0 .

^{— f} 0     \

^— 4 ⁽ f 1 ⁺ if 2 ) I _;

^— 4 ⁽ id 2 ^— d 1 ) I ’

-d 0

(29) его можно разложить в линейную суперпозицию:

f0  0  0  —f0       0  0  00

_ I 0   0  0    0  I I 0   0  00

=   0  0  0   0 + 0  0  00

0  0  0   0        d0  0  0

+

¹ 4 ^f 1 0

f 1

-

— 0 0

— 0 0

¹ 4 ^f 1 0

+

(  0     0  0   0\

0     0   00

+ I — 4 d 1   0   0  4 d 1

0     d1  00

+

0 ¹ ₄ f 2 0 0

f 2

0 0

-

0 ¹ ₄ f 2 0

+

0		0	0	0
+ I	0	0	0	0
	1 4 d 2	0	0	- 1 4 d 2
	0	0	d 2	0

Преобразование к этому базису найденных выше калибровочных решений Ф задается соотношением:

Ф f = Ф a — Y a Y b Ф ь , где Ф b = д ь Ф .     (31)

В результате для матрицы общего калибровочного решения в базисе Рариты–Швингера находим следующее представление:

Фк =

( —ikL 1 i ( e + k ) L 2     ( e + k ) L 2     ieL 1

+ ikL 2 i ( e — k ) L 1    — ( e — k ) L 1 —ieL 2

+ ikL 3 —i ( e — k ) L 4 — ( e — k ) L 4 —ieL 3

—ikL 4 —i ( e + k ) L 3    ( e + k ) L 3     ieL 4

Для ситуации e = k >  0 (с учетом последующего сокращения общего множителя e = k ) получаем

_Ф к

f 0 ^{K g} 0 ^K h^K h ₀

d ₀

^f 1 ^{K g} 1 ^K h ₁ ^{K d} 1 ^K

^f 2 ^K

f 3 ^K

g ₂

h ₂ ^{K d} 2 ^K

,К h3K d3K

/— iL 1 2 iL 2 2 L 2    iL 1 \

+ iL 2     0     0    —iL 2

⁼ + iL 3     0     0    —iL 3 ^.

—iL ₄ — 2 iL ₃ 2 L ₃ iL ₄

Это общее калибровочное решение можно разло- жить в суперпозицию четырех независимых

	—iL 1 0		0 iL 1		0	0	0	0
ФK =	I 0 0 0	0 0 0	00 00 00	I + I -	0 0 iL 4	0 0 0	0 0 0	00 II + iL 4
	+ I	0 + iL 2 0 0	2 iL 2 0 0 0	2 L 2 0 0 0	0 -iL 2 0 0		+
	+ I	0 0 + iL 3 0	0 0 0 — 2 iL 3	0 0 0 2 L 3	0 0 -iL 0	3	.	(34)

Первые два решения в (30) являются очевидно калибровочными, их можно отбросить, тогда остаются четыре решения:

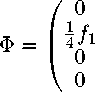
f 1

0 0

-

¹ 4 ^f 1 0

+

0 4 ^{i f} 2 0 0

0 f 2

-

4 ^{i f} 2 0

+

+I 0 0 0 0 0 0 0 0 - 14 d1 0 0 4 d 1 1 + 0 d1 0 0 /0 0 0 0 \ 0 0 0 0 +I 4id2 0 0 id I ;             (35) - 4 d2 0 0 d2 0 неиспользованными являются два калибровочных решения

	0	2 iL 2	2 L 2	0
(2)	I + iL 2	0	0	—iL 2 I
ф K	—0	0	0	0 ,
	0	0	0	0
	/ 0	0	0	0 \
Ф К * —	I 0 + iL 3	0 0	0 0	0 I -iL 3 .	(36)
	0 —	2 iL 3	2 L 3	0

Исследуем следующий вопрос: можно ли в решениях (35) выделить те, которые отождествимы с калибровочными решениями (36). Нужно решить уравнение

/      0

_{ф —} I 4 ( f 1 + if 2 ) I 4 ⁽ id 2 — d 1 )

f 1	f 2
0	0
0	0
d 1	d 2

— 4 ( f 1 + if 2 ) ^— 4 ⁽ id 2 ^— d 1 ) 0

I + iL 2

I ^{+ iL} 3

2 iL 2	2 L 2
0	0
0	0
— 2 iL 3	2 L 3

—iL 2 I

-iL 3

относительно переменных f 1 , f 2 , d 1 , d 2 . В результате находим два простых решения:

f 1 = 2 iL 2 , f 2 — 2 L 2 = ^ f 1 = if 2 ;

d 1 = — 2 iL 3 , d ₂ = 2 L 3 —^ d ₂ = id 1 .

Таким образом, найдены два решения, которые устраняются калибровочными преобразованиями (напоминаем, что параметры d 1 и f 2 независимые):

^f 1 — ⁺ if 2 , d 2 — ⁺ id 1 ,

	/ 0	if 2	f 2
ф— I	2 i f 2	0	0
	1 — 2 d 1	0	0
	0	d 1	id 1

- ₂ ⁱ f 2 2 ^{i d} 1

Ф —

Не устраняются калибровочным преобразованием следующие два решения:

f1 — —if2, d 2 — —id 1, ' 0 —if2 f2

0 d 1    —id 1 0

они не содержат калибровочных компонент и являются физическими.

Резюмируем результат. В явном виде построены шесть линейно независимых решений уравнения

для безмассовой частицы со спином 3/2, среди них найдены два решения, которые не содержат калибровочных компонент.