Структура пор в твердых пористых телах. Часть I

Развитие современной техники требует использования различных типов пористых материалов. Используются такие материалы, как адсорбенты, катализаторы, фильтрующие и теплозащитные материалы. Наибольший интерес и технологическую сложность среди подобных материалов представляют высокотемпературные теплозащитные материалы. Они используются как барьеры, разделяющие защищаемую конструкцию от воздействий внешней горячей среды, и выполняются в виде покрытий, облицовок, футеровок и более сложных теплозащитных систем. Они находят широкое применение в металлургии, литейном производстве, в авиации и космонавтике, в термоэлектрических преобразователях, в испытательных установках и машинах для исследования различных материалов и конструкций, в малоинерционных муфельных высокотемпературных печах и в ряде других отраслей техники [1]. Строение пористых материалов оказывает большое влияние на все эксплуатационные характеристики получаемых из них изделий. Этот факт характерен для пористых материалов в значительно большей степени, чем для плотных материалов.

В нашей предыдущей статье [2], посвященной пористым материалам, мы подробно осветили состав и структуру пористых термостойких неорганических композиционных материалов.

Пористыми материалами в широком смысле слова называются твердые тела, содержащие в достаточно большом количестве пустоты, размер которых значительно меньше размера самого тела. Обычно такие материалы формируются из дисперсных частиц различной формы. Пористая структура таких материалов формируется из характера упаковки их структурных единиц. Для удобства и простоты понимания сути явлений, связанных с формированием пористых структур, пористые материалы можно разделить на 3 группы. К первой группе мы отнесли материалы, сформированные из сферических частиц. Ко второй группе – материалы, сформированные из волокон. И к третьей группе отнесли пенообразные материалы. Такое разделение обусловлено тем, что форму частицы порошкообразных материалов можно в определенной степени аппроксимировать сферической формой. Вытянутые частицы можно асимптотически рассматривать как волокна. А остальные пористые материалы можно с определенным приближением представить в виде регулярной пены.

• 1.    Упаковка сферических частиц

Система пор в твердом теле всецело определяется характером упаковки первичных частиц. Так, например, при плотневшей гексагональной упаковке сферических частиц между расположенными в плоскости ближайшими тремя тетраэдрическими пустотами находится октаэдрическая пустота. При последующих наслоениях над октаэдрической пустотой возникает снова октаэдрическая пустота. Накрадывающиеся друг на друга октаэдрические пустоты образуют каналы, пронизывающие все тело вещества во взаимно перпендикулярных направлениях [32].

В кубических структурах плотнейшей упаковки можно также указать на образование взаимосвязанных каналов. В упаковках данного типа объем пустот составляет 25,95%. Отсюда можно рассчитать объемную массу материала ( ρ ):

ρ = ρ _k (1– α ),

где ρ _k – кристаллографическая плотность материала, используемого в качестве основы, α – доля пустот в структуре упаковки.

Если наиболее легкие среди огнеупорных материалов имеют кристаллографические плотности, близкие к 3 г/см3, то объемная масса продукта с плотнейшей упаковкой составит 2,2 г/см3. Отсюда для получения материалов с объемной массой, меньшей 0,5 г/см3, необходимо добиться пористости, большей 83%.

Попытаемся проанализировать, в каких системах упаковки можно достигнуть заданной и максимальной пористости.

Обычно с уменьшением координационного числа упакованных частиц растет объем пор в них. Для аналогии рассмотрим структурные типы кристаллических решеток простых химических веществ. Большинство металлических элементов и все инертные газы, за исключением гелия, кристаллизуется по простым структурным типам, а именно по типам A1, А2 и А3, А4. Все они могут считаться упаковкой шаров одинаковых радиусов [33]. Для случая A1 из плотнейших упаковок координационное число данной упаковки равно 12 (рис. 1). В этом случае мы имеем дело с плотнейшей кубической упаковкой, которая представляет собой геометрически возможную теснейшую укладку шаров одного радиуса. Классически плотность такой упаковки составляет 74%, соответственно пористость такой упаковки равна 26%. Для моноди-сперсных материалов более плотной упаковки не бывает.

Рассмотрим следующие варианты координационных чисел упаковки. Координационное число 8. Третий часто встречающийся металлический структурный тип – кубическая объемно-центрированная решетка А2. В отличие от плотных упаковок она имеет рыхлую структуру. Их кубическая ячейка содержит два шара, и решетка получается в результате взаимного сдвига двух примитивных (пустых) кубических решеток на половину телесной диагонали (рис. 2). Здесь шары в плоском слое не соприкасаются друг с другом, а находятся на расстоянии 0,155·R. Мотив постройки данной структуры характеризуется тем, что шары второго слоя опущены в пустоты нижележащего слоя. Третий слой повторяет первый, а четвертый – второй и т.д. Такой тип упаковки представляет свой оптимальный вариант пространственного расположения шаров с координационным числом 8. Далее на несколько большем расстоянии находятся 6 других соседей по вершинам октаэдра; отношение двух расстояний равно 1/2 Vb = 0,866. Такая структура обладает более низким процентом заполнения ее объема. Объем пор составляет 31,98%.

Координационное число 6. Простая кубическая упаковка. В ближайшем родстве с типом решетки А1 находится структурный тип А3;

87

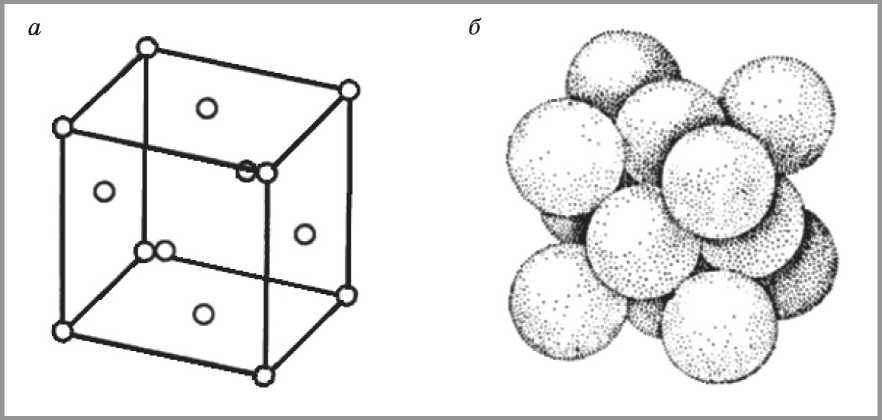
Рис. 1. Решетка кубической плотнейшей упаковки:

а) элементарная ячейка$ б) упаковка из соприкасающихся шаров он также построен из плоскостей плотнейшей упаковки шаров одинаковой величины, но порядок чередования плоскостей иной (рис. 2, 3). Существенно другое различие: если в структурном типе А1 расстояния между соседними атомами строго одинаковы и берутся из одного слоя или из соседних, то это связано с тем, что каждый атом окружен на одинаковых расстояниях с 12 другими атомами в вершинах архимедова кубооктаэдра. Однако в типе А3 гексагональной упаковки не всегда осуществляется действительно наиплотнейшая упаковка. Это происходит лишь, если отношение осей c/a будет составлять V8/3 = 1,633. Иначе говоря, здесь кроме геометрических параметров имеют значение и другие факторы.

Глобулярные структуры с координационным числом 6 построены путем последовательного наложения шаров, упакованных по квадратной сетке так, что центры шаров второго слоя располагаются строго над центрами шаров первого, третьего – над центрами второго и т.д. Пора в такой упаковке заключена между восемью контактирующими шарами и имеет шесть горл, имеющих форму, похожую на четырехугольную. При этом образуется более рыхлая структура, в которой объем пор составляет 47,64%.

Примером формирования таких структур являются природные и в особенности синтетические опалы. В синтетических опалах сфе-

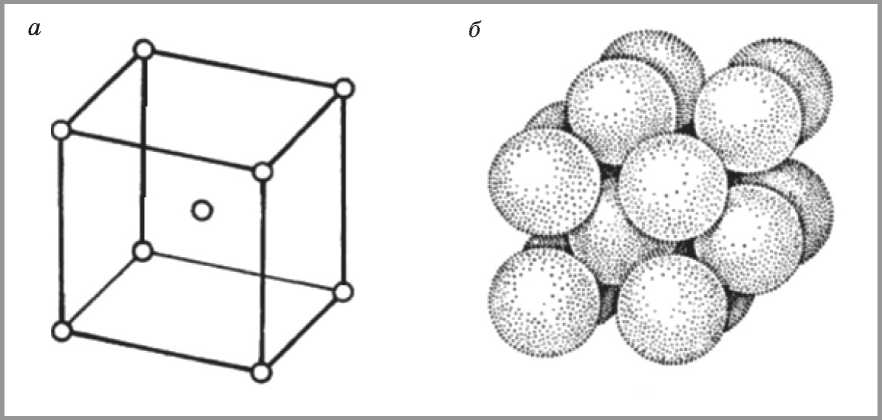
Рис. 2. Кубическая объемно-центрированная решетка:

а) элементарная ячейка, б) упаковка из соприкасающихся шаров (видны две смещенные друг относительно друга примитивные решетки)

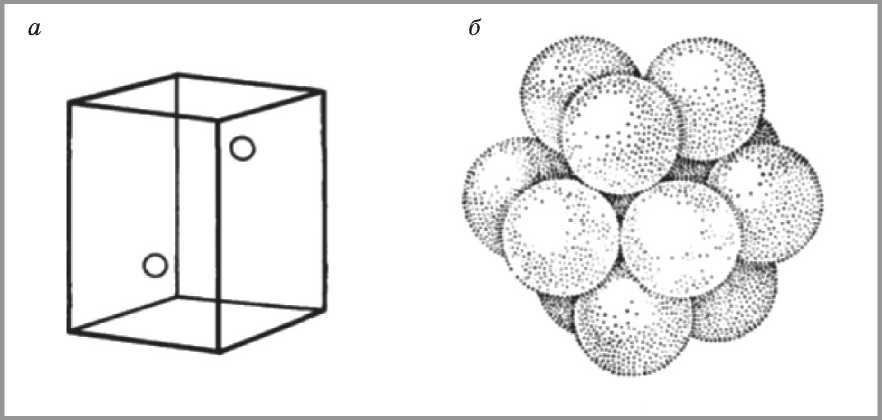
Рис. 3. Решетка гексагональной (двуслойной) плотнейшей упаковки: а) элементарная ячейка, б) упаковка из соприкасающихся шаров рические частицы диоксида кремния образуют высокоупорядоченные гексагональные плотноупакованные (ГПУ) слои перпендикулярно направлению оси роста опалового квазикристалла (рис. 4) [3, 4]. В случае трехмерной плотной упаковки возможны различные положения слоев:

периодическое чередование слоев в последовательности АВСАВС..., которое соответствует гранецентрированной кубической (ГЦК) решетке, последовательность АВАВАВ... формирует ГПУ решетку (рис. 4).

Тем не менее, ввиду малого энергетического выигрыша и значительной роли тепловой флуктуации в процессе роста синтетического опала последовательность чередования слоев вдоль оси роста образца может нарушаться и, в результате, во многом подчиняется вероятностному закону. При этом может образовываться плотноупакованная структура, неупорядоченная вдоль оси роста образца с произвольным порядком следования гексагональных слоев, например АВАСВАСА... В связи с этим структура опалов не является ни идеальной ГЦК, ни идеальной ГПУ решеткой. Благодаря случайной упаковке слоев в направлении оси роста в реальной кристаллической структуре опалов система ростовых плоскостей (111), перпендикулярных направлению оси роста, принципиально отличается от трех других систем плоскостей ГЦК решетки (-111), (1-11) и (11-1). Кроме того, случайное чередование ростовых слоев в синтетических опалах часто приводит к образованию двойниковых ГЦК структур, например ...АВСАВСАСВАСВА... [5, 6].

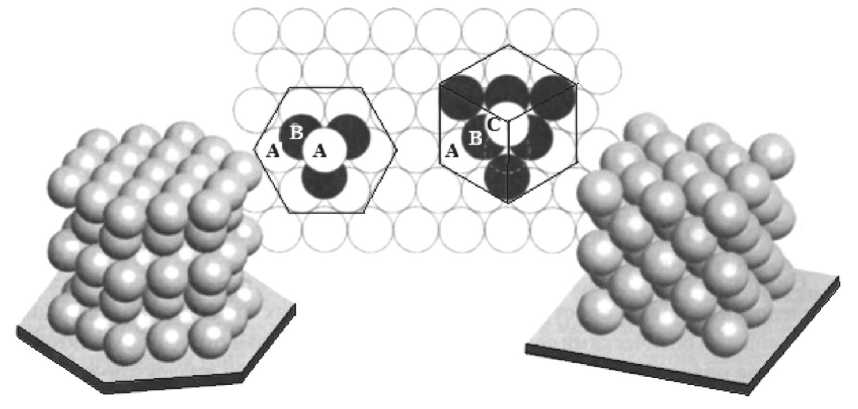
Рис. 4. Формирование плотноупакованной структуры сферических частиц: периодичность плотноупакованных слоев в гексагональной и кубической структурах, а также результирующие гексагональная плотная упаковка (ABAB…) и гранецентрированная кубическая упаковка (ABCABC…)

90

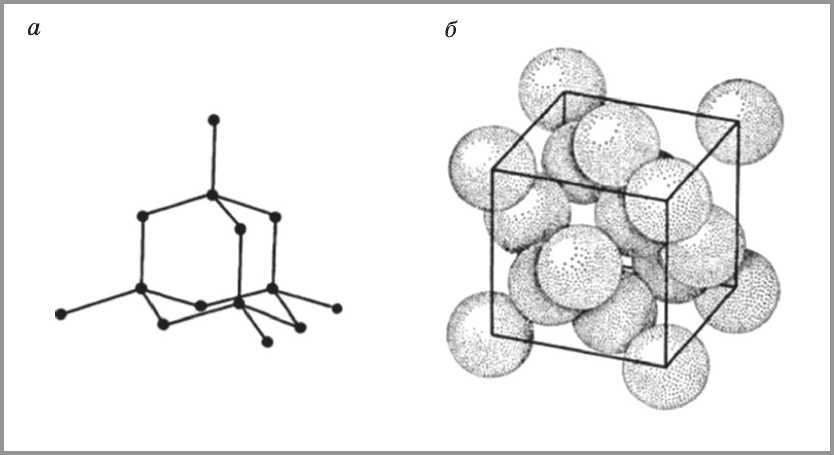
Рис. 5. Решетка А4 алмаза и льда:

а) координация атомов, б) упаковка в пределах элементарной ячейки

Координационное число 4. Классическим примером нужно считать решетку алмаза и льда типа А4. Этот структурный тип, относящийся к кубической системе, возникает, если мы вставим одну в другую две кубические гранецентрированные решетки со сдвигом на одну четверть телесной диагонали (рис. 5).

В получающейся решетке каждый атом окружен тетраэдрически четырьмя другими шарами, угол между направлениями от центрального шара к двум соседним при этом равен 109°28’. Данная упаковка наиболее рыхлая из всех рассмотренных. Построена она из слоев шаров, раздвинутых друг от друга в плоскости. Шары следующего слоя находятся между шарами первого слоя. Центры шаров третьего слоя расположены строго над центрами шаров второго. Четвертый слой расположен точно над первым и т.д. В результате такой упаковки объем пустот составляет 65,99%. В пределе (с уменьшением координационного числа) каждая симметрично построенная структура с заранее определенной системой пор должна перейти в хаотично сложенное тело с набором пор различных как по форме, так и по размеру. Структура такого материала и строение его пор приобретают фрактальную геометрию. Границей такого перехода можно считать упаковку с координационным числом 3.

Координационное число 3. Данная упаковка представляет собой очень ажурные, рыхлые образования с непрерывным трехмерным каркасом. Пористость этой структуры составляет 81,5%. Таким образом, опираясь только на различные виды упаковки сферических частиц, не удается достигнуть требуемой пористости и, тем более, достичь плотности менее 0,2 г/см3.

Однако, если допустить образование смешанной упаковки с координационным числом 2 и 3, то есть когда некоторые частицы в рассматриваемой упаковке присутствуют в виде коротких цепочек, состоящих минимум из трех частиц, то для таких упаковок можно достичь пористости 95%. На рис. 6 представлены структуры, образованные частицами с координационным числом 3 и 2.

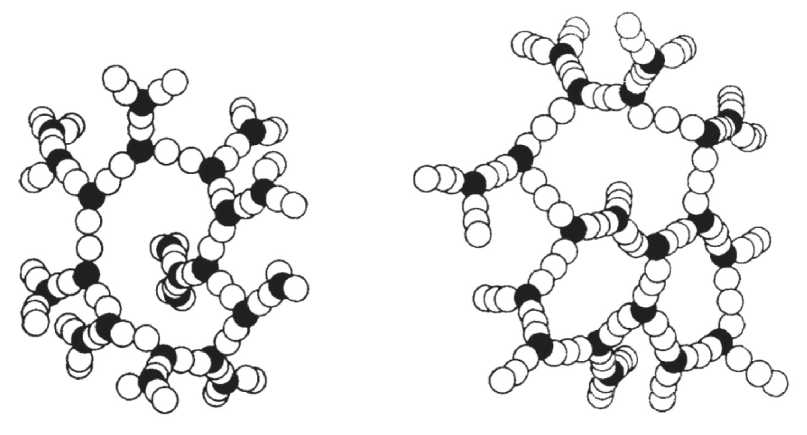
Рис. 6. Теоретические модели упаковки сферических частиц с «координационным числом»: 3, 2, 2, 3 и 3, 2, 2, 2, 3.

В черный цвет окрашенная каждая сфера, окружена тремя другими [28]

Из представленного рис. 6 видно, что эти модели упаковок весьма ажурные. Для них можно рассчитать средние значения координационного числа, приходящегося на одну частицу данной упаковки. Если выделить в подобной структуре элементарную ячейку, в центре которой расположена частица с координационным числом 3, а вокруг нее расположены цепочки частиц с координационными числами, равными

• 2,    то к каждой элементарной ячейке будет относиться ровно половина частиц из каждой цепочки. Отсюда среднее координационное число частиц в элементарной ячейке и, соответственно, во всей ажурной структуре будет представлять собой отношение суммы координационных чисел всех частиц в элементарной ячейке к числу частиц в элементарной ячейке. Если в структуре существуют смешанные образования с различными элементарными ячейками, то соответственно необходимо дополнительное усреднение по всем типам элементарных ячеек с учетом их доли во всей образованной структуре. Пример такого расчета представлен в табл. 1.

Таблица 1

Расчет среднего значения координационного числа для различных моделей теоретической ажурной упаковки сферических частиц

Параметры элементарной ячейки	Тип ажурной упаковки
	3-2-2-2-3	3-2-2-3	3-2-3	2 x (3-2-3) 1 x (3-3)	1 x (3-2-3) 2 x (3-3)	0 x (3-2-3) 3 x (3-3)
КЧ центральной частицы	3	3	3	3	3	3
Число центральных частиц в элементарной ячейке	1	1	1	1	1	1
КЧ периферийной частицы	2	2	2	2	2	2
Число частиц в одной цепочке периферийных частиц	3:2=1,5	1	0,5	0,5	0,5	0
Число периферийных цепочек	3	3	3	2	1	0
Общее число периферийных частиц	1,5 x 3 = 4,5	3	1,5	1	0,5	0
Суммарное КЧ периферийных частиц	4,5 x 2 =9	6	3	2	1	0
Суммарное КЧ всех частиц в ячейке	3+9 = 12	9	6	5	4	3
Общее число частиц в элементарной ячейке	1+4,5 = 5,5	4	2,5	2	1,5	1
Среднее КЧ	12:5,5 = 2,182	2,25	2,4	2,5	2,667	3

В табл. 1 совсем не рассмотрены варианты, когда могут возникнуть локальные элементы в структуре с КЧ = 4, что также может внести определенные корректировки в общий расчет среднего координационного числа в данной структуре. Эти данные еще раз показывают, что среднее координационное число в структуре может быть различным и, в том числе, дробным.

Зависимость пористости от координационного числа при различных способах укладки сфер представлена на рис. 7, откуда видно, что пористость обратно пропорциональна величине координатного числа.

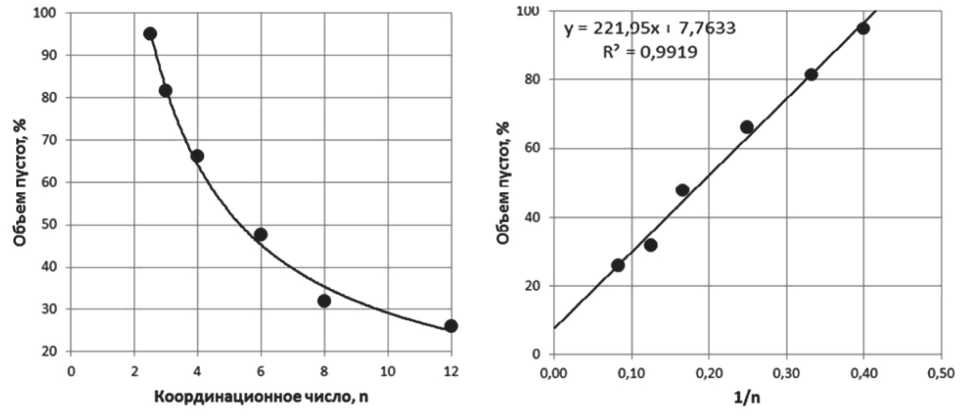
Рис. 7. Зависимость пористости упаковки сферических частиц от координационного числа n и 1/ n

В настоящее время материалы, в которых на долю пор приходится большая часть их объема, встречаются довольно часто, особенно среди различных сорбентов. Так, например, пористость силикагелей варьируется от 36 до 84% [7,8]. В работе [9] описано приготовление аэрогеля с пористостью 99%. Пористость различных аэросилов достигает 95 ^ 98% [10]. Аналогичные структуры формируются при диспергировании с помощью ПАВ волокнистых кристаллических силикатов типа хризотила. Образующиеся при этом отдельные волокна трубчатого типа [11] с диаметром 18 мкм вследствие переплетения создают очень рыхлые устойчивые коллоидные дисперсии с высоким значением пористости

• [12] . По-видимому, подобное сетчатое строение имеют лиогели, аэросилы и некоторые особенно рыхло-упакованные ксерогели, глобулярные цепочки которых связаны между собой так, что их число контактов для большинства глобул равно 2. Для придания жесткости скелету геля число соприкосновений частиц с соседями в узлах такой сетки должно быть равно 3. Но в любом случае такие структуры, построенные на основе сферических частиц, не будут обладать достаточной жесткостью.

Поэтому наиболее перспективным способом получения пористых материалов является применение различных волокон. Исходя из графика зависимости пористости α (%) от координационного числа n сферических частиц, приведенного на рис. 7, можно получить следующую зависимость:

α = α_∞ + B/n .                                                  (2)

Коэффициенты в этом уравнении для размерности dim( α ) = % имеют следующие значения: α_∞ = 7,763±0,016; B = 221,95±0,45, R² = 0,9959. Поскольку уравнение этой кривой имеет особую точку, то можно рассчитать предельное значение координационного числа, при котором объем пустот будет равен 100%:

n ₁₀₀ = (100– α_∞ )/B.                                                   (3)

Величина n ₁₀₀ = 2,406±0,010. Физический смысл этой величины заключается в том, что в структурах дисперсных наносистем при координационном числе меньше этой величины отсутствует сколько-нибудь жесткая структура каркаса материала, собранного из отдельных частиц. Ниже этого координационного числа частицы собираются только в отдельные цепочечные структуры, не связанные между собой, в которых реализуется координационное число 2.

Для описания зависимости пористости от координационного числа упаковки сферических частиц были проведены расчеты по подбору корреляционной зависимости, которая давала бы максимальный коэффициент корреляции. Максимальный коэффициент корреляции был получен для зависимости следующего вида:

α = α_∞ '+ B '/( n – n ₀).                                                  (4)

Коэффициенты в этом уравнении с условиями, как и в предыдущем случае, составили: α_∞ ' = 0,14964±0,00019, B ' = 310,10±0,40, n ₀ = –0,7750±0,0010, R ² = 0,9975. Полученная корреляционная зависимость представлена на рис. 8. Для этой зависимости также можно рассчитать предельное значение координационного числа, при котором объем пустот будет равен 100%:

n ₁₀₀ = n ₀ + B '/(100– α_∞ ').

Отсюда, подставив значения, полученные для выражения (4), получим следующую величину n ₁₀₀ = 2,331±0,006. Интерпретировать эти результаты сложнее, хотя они и дают более точный результат и несколько расширяют диапазон координационных чисел, до которых еще возможно образование жесткого каркаса, при ажурной упаковке сферических частиц.

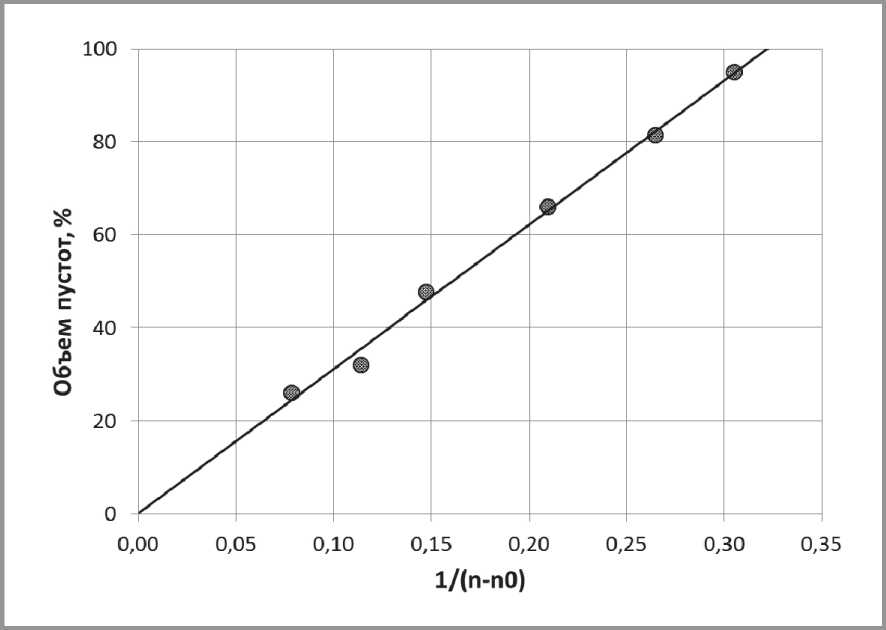
Рис. 8. Зависимость пористости упаковки сферических частиц от величины 1/( n – n ₀)

96

Полученные результаты указывают на то, что структуры, представленные на рис. 6, реально существовать не могут и являются исключительно теоретическими построениями. В реальных формирующихся структурах реализуется более плотная упаковка, чем предположенная Айлером в его классической монографии [28], хотя это нисколько не умаляет ценности его фундаментального труда.

Возможны два пути развития работ по созданию пористых материалов, обладающих высокой жесткостью. Первый из них – создание полостей внутри сфер, из которых упакована соответствующая структура. Зависимость объемной массы соответствующей структуры от параметров будет иметь вид:

/ /

^ ^^ ^         \      \           / ,                                                       (6)

где h – толщина стенки сферы; r_s – радиус сферы; α – пористость упаковки сфер.

Методы получения пористых материалов из пустотелых микросфер в настоящее время находят большее распространение. Однако получение пустотелых сфер является весьма сложной задачей, так как связано с применением низкотемпературной плазмы и низким выходом пустотелых сфер хорошего качества.

В последние десятилетия бурное развитие вычислительной техники привело к созданию принципиально нового мощного средства исследования физических процессов – вычислительного эксперимента. В условиях, когда теоретические методы наталкиваются на серьезные трудности, а практические эксперименты либо чрезмерно трудоемки, либо принципиально невозможны, численное моделирование оказывается единственным способом изучения рассматриваемых процессов. Создание компьютерных моделей стало в настоящее время признанным и быстро развивающимся направлением в науке и технике. Применение моделирования по сравнению с традиционными лабораторными методами экономит средства и время работы. В исследованиях, основанных на вычислительных экспериментах, решающую роль играет представление физического явления в виде соответствующей математической модели, вычислительного алгоритма, компьютерной программы. Математическая модель в вычислительном эксперименте является одновременно исследуемым материалом и алгоритмом его проведения. В работе

97

• [13]    показано, что одним из широкораспространенных методов построения математических моделей является моделирование с помощью частиц или метода частиц.

Указывается также, что при правильном использовании метод частиц в состоянии продемонстрировать свои явные преимущества. На основе накопленного теоретического и экспериментального материала [13–15] построена компьютерная модель дисперсных систем, основанная на методе частиц.

Метод частиц является общим для класса моделей, в которых дискретное описание физических явлений включает рассмотрение взаимодействующих частиц. Любую классическую систему можно описать, зная положения и скорости частиц, которые ее составляют, и закон их взаимодействия. Каждая частица имеет ряд сохраняющихся характеристик (например, массу и размер) и меняющихся характеристик (например, положение и скорость).

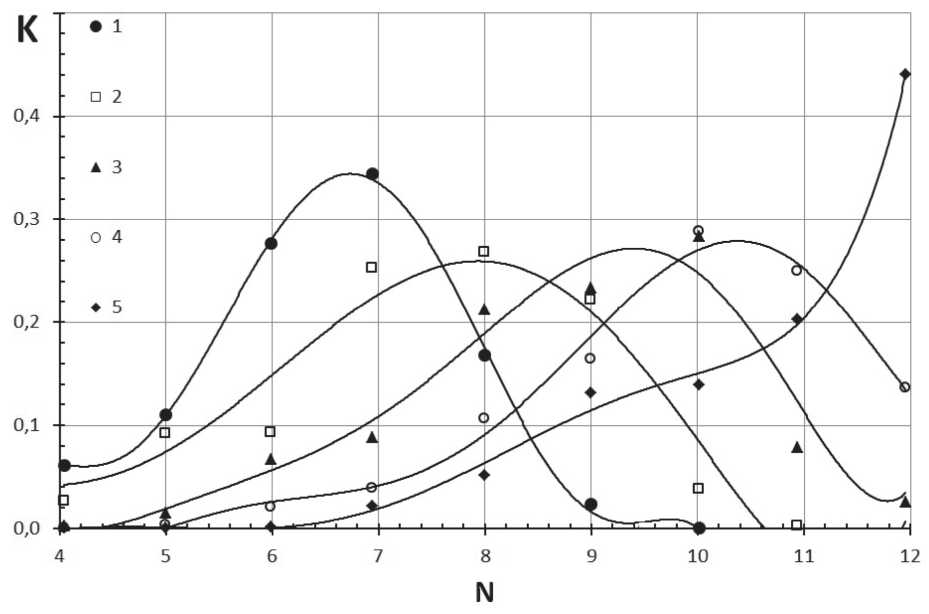
Рис. 9. Распределения координационных чисел для различных объемных наполнений порошка: 1 – 0.56; 2 – 0.58; 3 – 0.60; 4 – 0.62; 5 – 0.64

98

В качестве объекта численного исследования дисперсных систем методом компьютерного моделирования был выбран порошок алюминия. Это обусловлено тем, что частицы алюминия имеют сферическую форму. В результате проведенных вычислений были получены различные степени объемного наполнения под действием сжимающей силы. Из представленных на рис. 9 данных распределения координационных чисел для различных объемных наполнений порошка следует, что предельное объемное наполнение порошка, равное 64%, соответствует состоянию, когда более чем 40% частиц имеет координационное число 12.

Компьютерная модель также дает возможность изучать природу контактов между частицами в дисперсной системе. Были проведены вычислительные эксперименты по исследованию расстояния между «контактирующими частицами». На рис. 10 представлены распределения числа парных контактов в зависимости от расстояния между частицами для различных объемных наполнений. Из рис. 10 следует, что для всех объемных наполнений зависимость распределения парных контактов частиц от расстояния между ними имеет два максимума. Уменьшение объемного наполнения системы приводит к смещению максимумов в область большего расстояния между частицами.

Хранение и переработка порошка в реальных условиях сопровождается поглощением им влаги из окружающей среды в результате адсорбции паров воды на поверхности частиц и ее капиллярной конденсации в порах материала. Образование жидкой фазы приводит к появлению жидких «мостиков» и капиллярных сил между частицами порошкообразного материала. Эти силы оказывают существенное влияние на поведение и свойства порошков и дисперсных композиций, как при хранении, так и при использовании в технологических процессах.

Значительное влияние на величину этих сил оказывают геометрические параметры частиц. В частности, их размеры и форма частиц, обуславливающие тип «контакта» между ними. Следовательно, определение влияния геометрических параметров частиц порошка на величину капиллярных сил, действующих между ними, позволяет полнее прогнозировать свойства и поведение порошкообразных компонентов, а также будет способствовать получению на их основе дисперсных материалов с заданными свойствами.

Предложенный метод позволяет также определить количество жидкости в капиллярных «мостиках» между частицами и величину

99

МОДЕЛИРОВАНИЕ СТРУКТУР НАНОКОМПОЗИТОВ

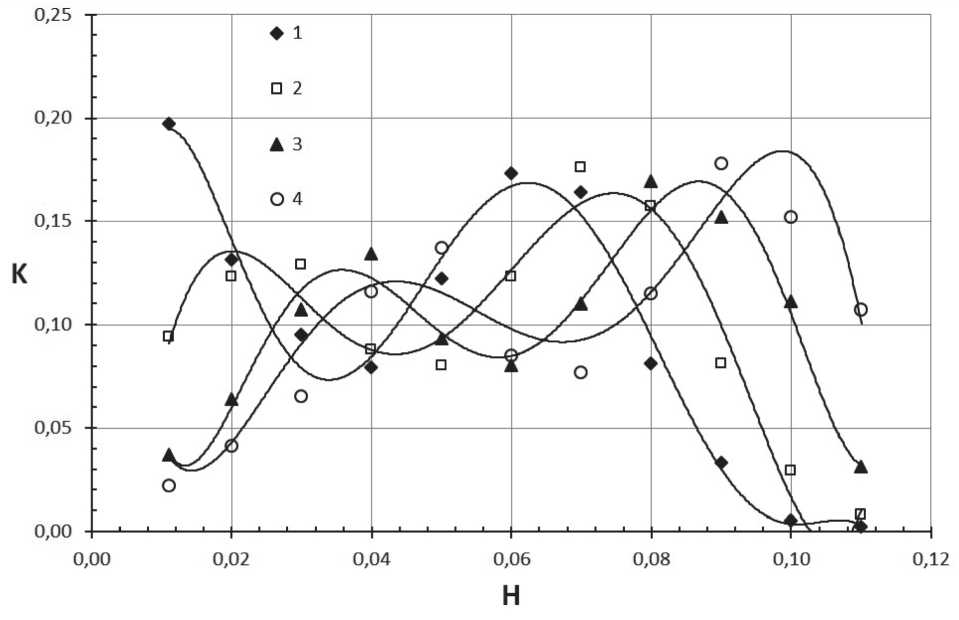
Рис. 10. Распределения парных контактов частиц в зависимости от расстояния между ними для различных объемных наполнений системы:

1 – 0.64; 2 – 0.62; 3 – 0.60; 4 – 0.56

капиллярного давления как параметра, определяющего одну из составляющих капиллярных сил [16]. В качестве расчетной ячейки было рассмотрено капиллярное взаимодействие двух соединенных жидким «мостиком» частиц, имеющих формы сферы, конуса и плоскости. Значительное число различных типов «контакта» частиц в реальных дисперсных системах может быть описано с помощью выбранных форм.

Величина капиллярной силы при этом, как и в случае сферических частиц одинакового размера, зависит от двух составляющих. Первая определяется поверхностным натяжением жидкости, действующим по периметру смачивания. Вторая составляющая обусловлена наличием в жидкости разряжения или давления, описываемого уравнением Лапласа и возникающего вследствие искривления поверхности «мостика».

Видно, что во всех случаях рост количества жидкости сопровождается появлением максимума капиллярных сил. Увеличение капилляр- ных сил происходит и с ростом отношения размеров частиц (рис. 11), сопровождающимся также приближением величин сил к значениям, соответствующим «контакту» частиц типа «сфера-плоскость».

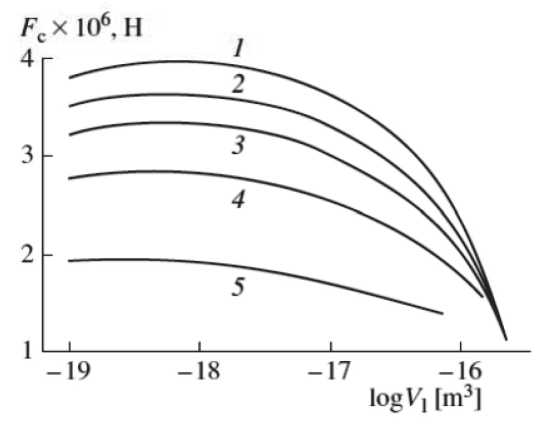
Рис. 11. Зависимость капиллярной силы от объема жидкого «мостика» при взаимодействии частиц типа «сфера-сфера». Радиус частицы равен 5 мкм.

Отношение радиусов частиц равно: 1 – 100; 2 – 10; 3 – 5; 4 – 2.5; 5 – 1

Однако с уменьшением различия между размерами частиц наблюдается снижение его влияния на капиллярные силы. Особенно это заметно при больших объемах жидкого «мостика», когда различия в величинах капиллярных сил становятся незначительными. На основании полученных данных было не только качественно подтверждено, но и количественно показано влияние различия в размерах частиц на величину капиллярных сил, действующих между ними.

С помощью полученных уравнений были определены зависимости капиллярных сил от количества жидкости в «мостике» для рассмотренных типов «контакта» частиц (рис. 12).

В качестве капиллярной жидкости рассматривалась вода. Для всех типов «контакта» величина зазора между частицами равнялась 0,01 мкм, угол смачивания составлял 0о. Из рис. 12 видно, что тип «контакта» частиц оказывает существенное влияние на величину капиллярной силы. Его влияние возрастает с увеличением объема «мостика».

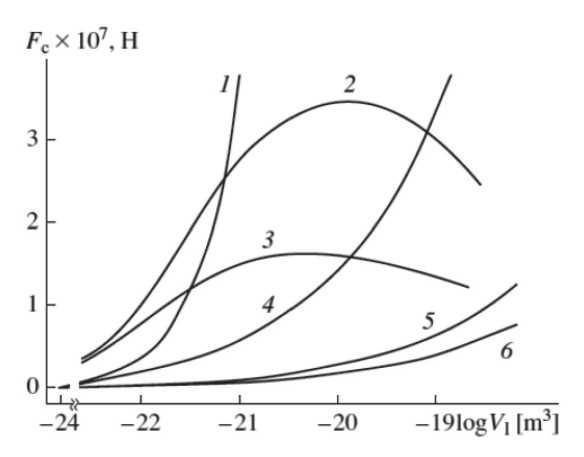
Рис. 12. Зависимость капиллярной силы от объема жидкого «мостика» для различных типов «контакта» частиц:

1 – «плоскость-плоскость» ( d = 0.2 мкм); 2 – «сфера-плоскость» ( R = 0.5 мкм);

3 – «сфера-сфера» ( R ₁ = R ₂ = 0.5 мкм); 4 – «конус-конус» ( β ₁ = β ₂ = 150^о);

5 – «конус-плоскость» ( β = 90^о); 6 – «конус-конус» ( β ₁ = β ₂ = 90^о)

На основе предложенных моделей были описаны и экспериментально проверены реологические свойства органоминеральных нанодисперсий и возможности получения на их основе токопроводящих полимерных композитов [17, 18].

Часть 2 статьи Кудрявцева П.Г «Структура пор в твердых пористых телах» читайте в номере 6/2018 Интернет-журнала «Нанотехнологии в строительстве».

Список литературы к частям 1, 2 статьи Кудрявцева П.Г «Структура пор в твердых пористых телах» будет опубликован также в номере 6/2018 Ин-тернет-журнала «Нанотехнологии в строительстве».

102

МОДЕЛИРОВАНИЕ СТРУКТУР НАНОКОМПОЗИТОВ

У важаемые коллеги !

П ри использовании материала данной статьи просим делать библиографическую ссылку на неё :

D ear colleagues !

T he reference to this paper has the following citation format :