Структура поверхности раздела частично смоченного диска с радиальными лопатками

Высокооборотные насосные агрегаты (НА) широко применяются в качестве агрегатов для подачи жидких рабочих тел в энергодвигательных установках летательных аппаратов (ЛА), ротор которых состоит из различных типов рабочих колес, дисков, систем уплотнений и т. п. [1].

Вопросам исследования гидродинамики по торцевой поверхности вращающегося диска посвяще- ны работы [2–4], авторы которых принимают в расчетах, что границы раздела жидкостной и газовой фаз представляют собой размытую цилиндрическую поверхность. Такая неопределенность с положением расчетных параметров вносит существенную погрешность при расчете элементов вспомогательного гидравлического тракта насосного агрегата [5].

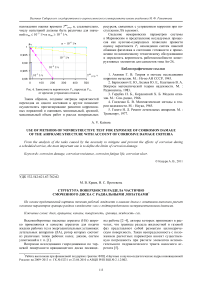
Картина течения между вращающимся диском с торцовыми лопатками (рис. 1) и гладким корпусом довольно сложна [1]. Жидкость, находящаяся в области каналов, подвергается непосредственному силовому воздействию лопаток. При бесконечно большом числе лопаток жидкость в межлопаточном пространстве РК будет вращаться как твердое тело с окружной скоростью ω _ж . Уравнение равновесия элементарного объема жидкости, расположенного межлопаточном пространстве на радиусе R толщиной dR в системе координат, скрепленной с этим объемом:

dp -ρ _ж ω ² RdR = 0 ,              (1)

где второй член левой части уравнения характеризует величину центробежной силы.

Рис. 1. Диск с лопатками (к принципу работы)

Интегрируя уравнение (1) в пределах от R г до R 2 , получим величину избыточного теоретического давления на внешнем радиусе диска:

Δ p 2 = p 2 - p г =ρ ж ω ² ( R 2² - R г² ) /2. (2)

Как показали экспериментальные исследования, жидкость закручивается в области зазора со стороны лопаток со скоростью, меньшей скорости вращения диска. Зависимость между угловой скоростью жидкости ω _ж и диска ω имеет вид

ω _ж =ϕω . (3)

Тогда зависимость между давлением на периферии диска и радиусом границы раздела фаз R г может быть выражена в следующем виде:

p 2 - p г =ρ ж ω ²ж ϕ ²ж ( R 2² - R г² ) /2. (4)

Поскольку коэффициент закрутки потока φ < 1, и всегда имеет место относительное движение жидкости и лопаток диска, что непременно приводит к образованию в каналах циркуляционной зоны, как следствие обтекания потоком впадин. В относитель- ном движении жидкость обтекает каналы со скоростью

W = ( U - U ж ) = U ( 1 -ϕ ж ) .           (5)

Известно, что при течении жидкости в канале за плохо обтекаемым телом (в нашем случае каналы и лопатки диска) возникают отрывные течения. Отрывное течение характеризуется образованием возвратных потоков и вихрей. Этот процесс в большей мере определяется отношением глубины впадины, толщиной пограничного слоя на стенке перед каналом и относительной высотой стенок канала. Взаимодействие между струей и жидкостью в канале приводит к появлению циркуляционного течения в зоне за выступом [6].

Сдвиговые течения в окружном направлении, в виде отставания закрученного потока в осевом зазоре компенсируются радиальным (расходным) течением в области каналов от центра к периферии, что характеризуется соотношением радиальной составляющей скорости V_R в канале от окружной V_U . Это дает основание выразить скорости радиального (расходного) течения жидкости в канале с учетом угловой скорости жидкости в окружном направлении в виде

V R =ω ж ⋅ R ⋅ K , (6)

где K – экспериментальный коэффициент K = 0,18 ± 0,03.

С учетом различной геометрии радиальных каналов диска зависимости для средней скорости радиального расходного течения на радиусе R в каналах числом z, постоянной ширины b и глубиной h полу- чим в виде

2πωR2a ⋅ K ⋅ ϕл

R b⋅h⋅z , для диска с лопатками постоянной толщиной δ:

V   2 πω R ² a ⋅ K ⋅ ϕ _л

^{R =} h (2 π R - z ⋅δ )

.

Расходное течение в каналах диска сопровождается сдвиговым потоком по аналогии с рабочим колесом центробежного насоса, что приводит в каналах диска к сдвигу поверхности раздела фаз «жидкость– газ». Для получения отпечатков и анализа течения в области осевого зазора и каналов диска в рабочую жидкость вводились примеси, которые осаждались на поверхности диска. Такой примесью в опытах авторов [7] служила вакуумная замазка, предварительно расплавленная в горячей воде. Кроме того, проводились испытания при подаче в центральную полость нагретого газового потока с высоким содержанием сажи, частицы которой осаждались на диске только в области свободной жидкости.

На фотографии, представленной на рис. 2, видно, что жидкость с напорной стороны канала опускается ниже границы раздела фаз R _г , имеющей место в зазоре a , на величину сдвига ΔR.

Исходя из представленной физической модели радиального одномерного течения жидкости в каналах, рассмотрим равновесие элементарного объема жидкости в канале у поверхности «жидкость–газ» (рис. 3). На выделенный объем жидкости массой dm действует центробежная сила инерции dm го ² R и кориолисова dm 2 го V R . Сумма проекции всех сил, действующих на элемент с учетом, что dR / db = tg a , запишется:

2V_r - db -го- R - dR = 0. (9)

у [ Rr2-( R-AR )2

= 2 b r - V r .

С учетом выражений (7) и (8) уравнение для определения величины сдвига границы раздела фаз частично смоченного вращающегося диска получим в виде:

25,12 aK ф _л z - h

A R = R _r 1 -

Рис. 2. Диск с радиальными лопатками

Для одномерного расходного течения по ширине канала диска величиной b равнодействующая всех сил на границе раздела фаз уравновешивается силой дав-

ления прилегающих слоев жидкости, и поэтому поверхность жидкости нормальна к этой равнодействующей, что обусловливает сдвиг поверхности раздела фаз под углом:

dm го- VR 2Vr

RR

.

dm го R   го R

Для величины сдвига по границе раздела фаз на радиусе диска R г в канале величиной b можно записать:

AR =

2 b r - V r го R

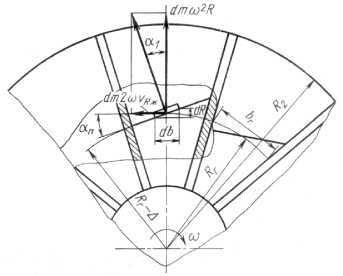
Рис. 3. Расчетная схема положения границы раздела «жидкость–газ» по ширине канала вращающегося диска

Интегрируя уравнение (9) при условии, что давление в газовой полости – величина постоянная и равна давлению на границе раздела фаз, получим:

Для границы раздела фаз величины R г имеем:

A R =

4 n R - a - K - ф _л h - z

По полученным зависимостям (11) и (14) с учетом экспериментальных значений kR = 0,18 и ф = 0,8 ж были просчитаны величины сдвига ΔR для различных дисков в широком диапазоне изменения режимов их работы (см. таблицу).

В таблице представлены результаты расчетов и экспериментальные значения величины Δ R при испытании на различных рабочих жидкостях в широком диапазоне изменения угловой скорости диска с разной формой каналов. Как видно из таблицы, расчетное значение величины сдвига поверхности жидкости в каналах диска удовлетворительно согласуются с экспериментальными данными.

Величины сдвига Δ R для различных дисков в широком диапазоне изменения режимов их работы

Форма канала	ω, рад/с	Рабочая жидкость. Плотность, кг/м 3	R г , мм	A R экспер , мм	R г , мм
Л	2 620	Этиловый спирт, 800	29	2,1–2,3	2,48
П	2 140	Вода, 1000	34	3,6–3,8	3,42
П	2 040	– || –	28	2,5–2,8	2,81
П	1 110	– || –	34	3,2–3,5	3,42
П	1 050	– || –	23	2,5–2,9	2,31
Л	2 100	– || –	33	3,1–3,3	3,32
Л	1 110	– || –	32	3,0–3,1	3,22
П	3 770	Азотная кислота, 1 140	22	2,0–2,2	2,21

Примечание : * Ввиду размытой границы следа измерялось два значения Δ – по верхней и нижней границе; Л – лопатка постоянной величины, П – паз постоянной величины.