Структура сжимаемых вихревых течений Куэтта-Тэйлора

Исследованию течений несжимаемой жидкости посвящено много работ. В то же время с точки зрения технологических приложений и фундаментальной науки анализ течений сжимаемого газа, имеет несомненный интерес. Обычно важным методом исследований являются численные методы анализа. Был опубликован ряд статей [1], в которых представлены результаты решения уравнений Навье-Стокса для сжимаемого газа.

В настоящей работе рассматриваются течения сжимаемого газа, между вращающимися цилиндрами. Анализ ограничен рассмотрением больших чисел Рейнольдса.

На практике могут реализовываться и течения с конечными числами Рейнольдса. Течение в таком случае описывается обычными уравнениями Навье-Стокса, нелинейными или линейными, в зависимости от рассматриваемых задач (описания среднего течения или исследовании устойчивости). Понятно, что для решения таких задач единственным способом является применение численных методов, основанных на использовании конечных разностей или представлениями в виде разложений в ряды.

Ситуация с рассмотрением течений при больших числах Рейнольдса, приводит к появлению сингулярности в уравнениях Навье-Стокса, что требует или введения адаптивных сеток, или применения асимптотических методов, например таких, как метод сращиваемых асимптотических разложений или других и создания с их использованием соответствующих моделей. Такой путь ранее был применен к анализу течений открытого типа -в пограничных слоях на. искривленной поверхности [2], в результате был выявлен целый класс решений, соответствующих различным длинам волн.

Аналогичный анализ можно провести и для течений закрытого типа, (между вращающимися концентрическими цилиндрами). Аналогом толщины пограничного слоя здесь выступает расстояние между стенками. Иерархия режимов может быть построена для разных величин отношения длин волн возмущений к величине зазора.

При анализе течений с большими числами Рейнольдса, возникает вопрос о сосуществовании инерционного и вязкого течений. Под вязким понимается течение, описывающееся только диссипативной частью уравнений Навье-Стокса. На самом деле даже без предположения об отсутствии инерционности, только принимая условие одномерности течения, можно получить описание с диссипативными членами (как в случае несжимаемой жидкости [3-4].

При преимущественном влиянии инерционных эффектов уравнения не содержат диссипативных членов вообще, поэтому обычной является схема, рассмотрения задач, для которых (при любых числах Рейнольдса) на. основное течение, описывающееся диффузионными членами, накладывается возмущение, описывающееся инерционными членами. Таким образом можно исследовать линейные и нелинейные режимы.

Ситуация с большой величиной параметра (пропорционального отношению величин инерционных членов к диффузионным) приводит, как и для течений открытого типа, к локальным задачам, описывающим квадратные вихри с асимптотически одинаковыми размерами в направлениях у и г.

Можно показать, что возмущенное течение описывается в этом случае параболизованными уравнениями Навье-Стокса для несжимаемой жидкости с локальными термодинамическими величинами, соответствующими местоположению вихря (расположенному около одной из стенок или всплывшему).

Более интересными оказываются течения, в которых действительно сказывается влияние вязкости, а именно в таких, для которых размер вихря в направлении у сравним с величиной зазора.

Естественно начать анализ с таких длин волн возмущений или вихрей, размер которых в направлении г также совпадает с величиной зазора.

В настоящей работе приведены результаты асимптотического анализа течений сжимаемого газа для случая больших чисел Рейнольдса и малых (по сравнению с радиусами цилиндров) величин зазора между поверхностями. Сформулированы соответствующие математические задачи и найдены параметры подобия.

2.    Постановка задачи

Исследуется течение между двумя концентрическими цилиндрами бесконечной длины, которые вращаются с различными угловыми скоростями. Предполагается, что поверхности цилиндров имеют различные температуры. Вводится цилиндрическая система координат.

Для координат и функций течения вводятся следующие обозначения: tR i /W i, гR ₁ , rR 1 ,w, uW 1 , vW 1 , wW 1 , p o W², p _s p, HW², p _s p, aW 1 соответственно для времени, осевой, радиальной и угловой координат и для соответствующих компонентов вектора скорости, для статического давления, плотности, полной энтальпии, для коэффициента вязкости и для скорости звука. Индекс «1» соответствует параметрам внутреннего цилиндра (в случае если внутренний цилиндр покоится, используется скорость внешнего цилиндра). Индекс « s» соответствует значениям термодинамических функций газа в условиях отсутствия вращения цилиндров.

3.    Система оценок

Оценим вначале перепад давления между стенками цилиндров, возникающий под действием центробежных сил

Ар ~xd,                                    (1)

предполагая, что скорость в окружном направлении порядка единицы, d - ширина зазора между цилиндрами, а х = R^-1 ~ кривизна.

Индуцируемая этим перепадом скорость в направлении г (предполагая, что перепад давления в радиальном направлении такой же, как и в трансверсальном) оценивается следующим образом:

w ^\' 2d1 2.                                                  (2)

Эта оценка, строго говоря, имеет место, если силы вязкости несущественны. Мы рассматриваем именно режимы, для которых или вязкость несущественна, или граничные, для которых вязкость и инерционные силы сравнимы.

Поскольку мы ограничиваемся режимами, где от окружной координаты ничего не зависит и неустойчивость (в отличие от вихрей Тэйлора-Гертлера на пластине) развивается как нестационарный процесс, то уравнение неразрывности в невырожденном виде должно содержать производные как в радиальном направлении, так и в трансверсальном. Тогда при заданном масштабе по г, характеризующемся величиной А:

w г           x^ /^ d? / ²

Ad     А

Оценим теперь в уравнении радиального импульса влияние вязкости

11 ~ 2 ” „„„ Д, ~ d     d2              А

, где е = Re ^1/2,

то есть имеется такая иерархия. Если зазор и длина волны сравнимы, тогда, если они совпадают с этим вязким размером, получатся параболизованные уравнения Навье-Стокса, в которых вязкость работает в двух направлениях: в радиальном и трансверсальном. Если эти размеры больше вязкого размера, тогда у нас получаются уравнения Эйлера.

Далее, если длина волны больше зазора, тогда есть предельная длина волны, при ко- торой в течении проявится влияние сил вязкости, но уже только радиальном. Поэтому

в

одном направлении -

Эр Эри Эру at +    +    + ру = 0, дри , дри2 .др.дрито , 1         ЕгЛо_d   ди _ ді + дг + дг + дг + г риу = Re { 3 [2 дгР( дг + 3 [ дг р(—ди+2 дг — г]+^[ ди +fe).

Эм дг

—

I „ )] +

^дри , дри? , ^дри ² , ^дР , „„,2

"дТ ⁺ "дГ ⁺ дг ⁺ дг ^{+ ру —} Р^ , 2 д ди ,₂дм_мп _2 щ_г_, ⁺ 3 дг ^{Р [} дг ⁺² дг г ^]) 3 Re ^[ ,

—

,² = 1 { [ 8 р( 8" + 8м ] +

Re L L дг ^Р Эг ¹ аг' ди — о? + 2 1 ] , дг дг 1 ,

°д + r^w + W ₊2 1     = 1 » [„dw ] + 1 » [ „ » , w + ^ )] +

ді      дг       дг       г ^р       Re дг ^Р дг Re дг ^Р дг г дг

₊ JL [ _— , ₊ °w ]

+ Re [ г + дг ], дрЕ + дриН + дриН + 1 р„я =   { 2 д ^п[2ди — д? _ 1 „] + d р„[ди + д?] + ді дг      дг     гр       Re 3 дг Р дг дг г дгр дг дг

+ Ри [ 0" + 0? ] + 2 р„ [ — Эи +2 д? — у ] + 2 ди [ — ди +2 д? _ у ] + д? [ ди + д? ] +

^Р дг дг 3 ^Р дг дг        3 дг дг дг        дг дг дг

+ тт [ри( От + Э? )] + 2 д [ р„ ( — ди +2 д? _ ? )] + ди [ ди + д? ] + 2 д? [ — ди +2 д? _ „ ] +   ₍₉₎

¹ дг ^Р дг дг 3 дг ^Р дг дг г дг дг дг 3 дг дг дг

-I__¹ , Г 8 дт дт , д дт

⁺ Pr(7 - 1)M ² Re ^[ дг ⁽Р дг ) Р дг ⁺ дг ⁽Р д ‘ г ^{)] +}

+ Т1 э-^Р⁸,   1- 0-\p4-^w + эг)1 + T1^w (-^w + Әлі.

1 Re дг Р дг Re дг Р г 1 дг Re Р г 1 дг где Re = раи^К1, Рг - число Прандтля, М - число Маха.

Полученные оценки можно использовать для построения диаграммы возможных режимов. Анализируемые режимы располагаются внутри треугольника АВС. Наиболее общим, с точки зрения проявляющихся эффектов, будет режим, соответствующий точке А, где течение описывается параболизованными уравнениями Навье-Стокса. Термин «параболизованные» соответствует здесь отсутствию диссипативных членов в окружном направлении. Эти эффекты проявляются лишь в направлениях по радиусу и вдоль оси цилиндров. Соответственно параметры, находящиеся на линии АВ ниже точки А, соответствуют режимам, для которых вязкость уже не существенна, а длина волны вихрей совпадает по порядку величины с величиной зазора.

Линии АС соответствуют вихри, на которые влияет вязкость, а характерный размер зазора много меньше, чем длина волны (рис. 1).

Итак, введем следующие представления координат и функций течения:

г = А^1, т = йт1, t = d 1/2t1A, w = wo + ..., и = d1/2u1 + ...,    у = d3/2A 111 + ..., p = po + dp1 + ..., р = ро + ...

Подстановка разложений в исходную систему уравнений дает

Эр о + Эр о и т + Эр о У 1 dt 1      Эг 1       Эт 1

д^0"! + др0"1 + dpi + др°иіж = {2 [2 д_пщдГди — 8м )] + діі      дгі дгі      дгі        3 дг 1  2Р дг дг

+ 3 Л1 Р дг ( — % +2 0? ] ).

Эр о ^ о дt ₁

+ d ( p o n i w o ) + д ( р ощ ш о ) дг ₁           дг ₁

д Г дш]      _тт-1 д Г д /дш\]

— П1П2 . . /V      - П1П2 TH р .. ( Щ- ) , дг [ дг J 2 дг [ дг у дг у J

['Д'' + ^Д^ + "Д'²]П2 + 0^{е 1} - р^ = ЩП₂ { [ Д/ ( 0^е + п2Д] +

L 0t i    ¹      02 1     ¹ 0г 1 -I 2 ¹   0г 1     ^{р о}  0        ^{1   2} I 0 2 / ^р\ дг  ¹     2 02   ¹

⁺ 3 0 з ' ж ^{+ 2} °Г ^]},

SgE + Эрин + М. =     ¹ [п п₂ S ( / эт) + ЩП ^-1 0- ( р 0Т )] +

0t       02 ¹ дг Рт( Д — 1) М ^{2 L 1 2} 02 ™ 02 ' ^{1 1} 2 ОГ х^р дг^ ¹

+ П 1 П 2 Д [ w/^ ] + ЩП —¹ 0 [ /w ( Д )] ,

^ГЛ^{С П} 1 = Д/2- ^п 2 = Г

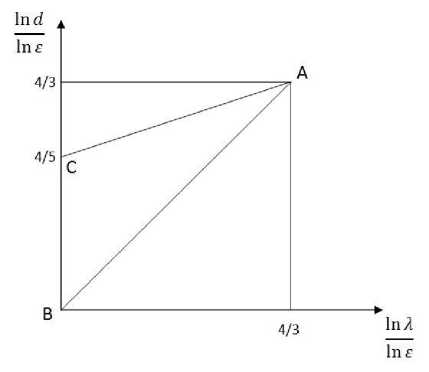
Рис. 1. Диаграмма, различных возможных режимов течения Куэтта-Тейлора.

Полученные параметры подобия имеют простой физический смысл. Параметр Щ определяет отношение диффузионных эффектов к инерционным эффектам. По существу, это обратная величина локального числа Рейнольдса. Параметр П2 определяет отношение ширины зазора, к длине волны пространственных возмущений (вихрей). Напомним, что во всех случаях мы имеем дело с безразмерными параметрами.

Общая система, уравнений соответствует точке А, для которой оба. введенных параметра, подобия сохраняют конечное значение.

Для дальнейшего анализа, отметим, что возможны различные предельные переходы. Если мы будем двигаться вдоль линии АВ, параметр П1 = 0, а параметр П2 сохраняет конечное значение. Система, уравнений для этого предельного перехода, имеет вид:

др о + др о щ + др о Г 1 = дt ₁      дг ₁       дг ₁

др о щ у + др о п ! + др 1 + др о П 1 Т 1 дt ₁       дг ₁      дг ₁       дг ₁

= 0 ,

др o w o + д (р о n 1 w o ) + д ( р о ^ 1 Ш о ) = 0

дt ₁          дг ₁            дг ₁

Г др о ^ 1 дt 1 ⁺

др о и р и 1 дг ₁

, ^д р о У р 1    2 , ^др 1

дг ₁     ²   дг₁

^{— р} о ^w 2 = ⁰,

дрowo + д (ро n1wo) + д(ро^1Шо) = 0 дt1         дг1            дг1         , дрЕ дриН дртН = о дt дг дг

Соответственно, параметры, находящиеся вдоль линии АС, приводят к режиму течения, в котором вязкость существенна (в одном направлении):

		dp o + dp o u i + dp o v i = о	(21)
dp o u i dt 1	dp o u i + 9z i	+Hi+ 'pT ' H (-du +2 * )]•	(22)
		£ [^ (t)] =0 ,	(23)
		§- - poW 2 = 0’	(24)
ЭрЕ dpuH at. + az +	dpvH Әк =	•      [” 1 1 ^ )Н H h ( £)].	(25)

4.    Выводы

В результате асимптотического анализа уравнений Навье-Стокса, описывающих течение сжимаемого газа между вращающимися цилиндрами, сформулированы математические модели для характерных режимов возмущенного течения. Определены параметры подобия и построена диаграмма режимов в условиях возникновения периодической системы вихрей.