Структурная динамика миграций между федеральными округами России в 2000-2015 гг.

Статистическая характеристика миграционных потоков представляет собой важный элемент социально-экономического мониторинга. К сожалению, такая характеристика обычно ограничивается расчетом относительных показателей структуры, исключая из рассмотрения структурные сдвиги и взаимосвязи. Цель настоящей статьи – хотя бы в некоторой мере восполнить этот пробел, проанализировав структурную динамику въездной миграции в разрезе федеральных округов Российской Федерации.

Межрегиональная миграция, являющаяся предметом данного исследования, – важнейший элемент миграционной ситуации страны, так как ее интенсивность, рассчитываемая как количество въездов мигрантов, превышает международную миграцию на 66,5% и составляет 1 158 130 перемещений в 2015 году [1]. В основу группировки федеральных округов России по структуре прибывших были положены следующие характеристики и индикаторы:

• 1.    Близость структур, определяемая с помощью парных индексов Рябцева [2] на основе попарных сравнений структур въезжающих по признаку территориальной принадлежности приехавшего;

• 2.    Динамичность структур, определяемая на основе базисных и цепных индексов Рябцева с базисной и переменной базой сравнения по каждому региону;

• 3.    Уровни концентрации, рассчитанные по формуле коэффициента концентрации Герфиндаля.

Для анализа были использованы данные о структуре въездной миграции в разрезе регионов исхода каждого федерального округа России за 2000-2015 гг. [1] Для обеспечения сопоставимости из анализа

ГРНТИ 06.35.33

Егор Витальевич Павловский – аспирант кафедры статистики и эконометрики Санкт-Петербургского государственного экономического университета.

были исключены данные по Республике Крым и Севастополю, вошедшим в состав Российской Федерации в 2014 г. В качестве обобщающих значений, необходимых для сегментации на основе иерархического кластерного анализа, использованы медианные значения по каждому из индексов. Выбор медианы в качестве показателя центра распределения обусловлен простотой интерпретации индикатора и небольшим размером выборки. Для удобства представления данных в таблицах каждому региону был присвоен код.

Расчет показателей для последующей многомерной группировки проводится в несколько этапов. На первом из них производится расчет попарных индексов Рябцева по формуле индексов Рябцева во времени [2], но в качестве сравнения используются доли региона (федерального округа), с которым оно производится:

j =

' ^(^Б)2, где dA, ^Б - удельные веса каждого региона в миграции двух сравниваемых регионов, в коэффициентах; i – число регионов исхода мигрантов.

Таким образом, в каждой паре формируется ряд значений индексов Рябцева, состоящий из 16 значений (соответствует количеству лет для сравнений), а в качестве обобщающего показателя определяется медиана по каждой паре. Полученные таким образом значения медиан для каждой пары приведены в таблице 1.

Таблица 1

Медианы значений попарных индексов сравнения структур Рябцева за 2000-2015 гг.

	ЦФО	СЗФО	ЮФО	СКФО	ПФО	УФО	СФО	ДФО
ЦФО	Х	0,167	0,233	0,373	0,283	0,258	0,327	0,323
СЗФО	0,167	Х	0,231	0,342	0,300	0,345	0,324	0,323
ЮФО	0,233	0,231	Х	0,202	0,319	0,384	0,299	0,323
СКФО	0,373	0,342	0,202	Х	0,390	0,498	0,412	0,441
ПФО	0,283	0,300	0,319	0,390	Х	0,222	0,274	0,437
УФО	0,258	0,345	0,384	0,498	0,222	Х	0,424	0,383
СФО	0,327	0,324	0,299	0,412	0,274	0,424	Х	0,210
ДФО	0,323	0,323	0,323	0,441	0,437	0,383	0,210	Х

Источник: собственные расчеты автора на основе [1].

Приведенные расчеты показывают, что наиболее близкими по составу регионов исхода мигрантов являются Центральный федеральный округ и Северо-Западный федеральный округ (индекс Рябцева равен 0,167), Южный федеральный округ и Северо-Кавказский федеральный округ (значение индекса составило 0,202). Наименее схожи структуры мигрантов Северо-Кавказского федерального округа и Уральского федерального округа, в случае сравнения которых индекс Рябцева составил 0,498, что согласно шкале оценки степени различий [2] говорит о значительной степени различий.

На втором этапе для оценки изменчивости структур каждого региона используются индексы Рябцева с постоянной и переменной базой сравнения. Для оценки качественных изменений в структуре изучаемого явления во времени необходимо уделять внимание структурным сдвигам. Общепризнанным и наиболее репрезентативным индикатором такого рода признан индекс Рябцева, т.к.он дает возможность его расчета в условиях равенства долей и наименее чувствителен к выбросам. Индекс Рябцева с переменной базой [2] характеризует общую вариабельность изменчивости структуры, а с постоянной базой - общее изменение структуры въезжающих в регион за исследуемый период с 2000 до 2015 гг.

Рассчитав значения индексов Рябцева для каждого региона, определяем для них медиану с 2001 по 2015 год с переменной базой сравнения, иллюстрирующую среднюю величину. В качестве индикатора общего изменения используем данные об индексах Рябцева с постоянной базой за 2015 год с базисным 2000 годом. Базисным был признан 2000 год по причине необходимости апробации методики на максимально длинных рядах, что делает результаты более точными. Результаты расчетов необходимых индикаторов представим в виде таблицы 2.

Таблица 2

Индикаторы изменчивости и уровня концентрации региональных миграционных структур

Регион	Медианное значение индекса Рябцева с переменной базой сравнения	Значение индекса Рябцева с постоянной базой сравнения (2015 к 2000 гг.)	Медианное значение индекса концентрации Герфиндаля
ЦФО	0,014	0,156	0,166
СЗФО	0,015	0,042	0,184
ЮФО	0,022	0,120	0,151
СКФО	0,023	0,202	0,202
ПФО	0,021	0,193	0,196
УФО	0,019	0,054	0,249
СФО	0,019	0,175	0,176
ДФО	0,015	0,092	0,212

Источник: собственные расчеты автора на основе [2].

Из данных расчетов медианных значений индексов Рябцева с переменной базой сравнения следует, что структуры въездной миграции всех федеральных округов Российской Федерации в рассмотренном периоде не претерпевали существенных изменений от года к году. Индексы Рябцева с постоянной базой сравнения показывают, что наиболее сильные изменения в структуре въезжающих по сравнению с 2000 годом произошли в Северо-Кавказском и Приволжском федеральных округах. Структура прибывающих мигрантов в Северо-Западном федеральном округе за 16 исследуемых лет осталась практически неизменной, что подтверждается значением индекса Рябцева, незначительно отличающимся от нуля. Такую же ситуацию можно отметить и в Уральском федеральном округе, где индекс Рябцева составил 0,054, что говорит о низкой степени различий структур и низкой степени изменчивости структуры въезжающих в регион.

На третьем этапе для оценки уровня концентрации использовался индекс Герфиндаля [3], отображающий неравномерность распределения групп мигрантов по региону исхода в совокупности, рассчитываемый на основе сумм квадратов долей. Данный индекс может принимать значения от 0 до 1, при этом чем выше значение индекса, тем более неоднородным является исследуемый объект. Так, например, если в регионе преобладают мигранты из одного региона исхода, индекс принимает большие значения. Полученные значения уровней концентрации (табл. 2) говорят о том, что структуры мигрантов достаточно однородны. Наибольшее значение коэффициента отмечается в Уральском федеральном округе, что объясняется преобладанием мигрантов из Приволжского федерального округа, удельный вес которого варьируется от 39,7% до 43,8% за исследуемые 16 лет. Во всех остальных регионах структуры менее разнородны и доли различаются незначительно.

После расчетов всех индикаторов, описанных выше, была произведена группировка регионов с помощью иерархического кластерного анализа. Выбор метода обусловлен возможностью графического представления процедуры группировки, что позволяет визуально определить количество необходимых кластеров. Метод измерения расстояний между кластерами – «метод Варда», минимизирующий внутрикластерный разброс объектов, что является необходимым условием при небольшом количестве объектов кластеризации. Исходя из того, что все группировочные признаки, используемые для кластеризации, являются количественными, мерой расстояния между кластерами выбрано Евклидово расстояние [4, с. 353-354].

Качество кластеризации было проверено различным сочетанием методов измерения расстояний между кластерами (в т.ч. межгрупповой связи, ближайшего соседа и внутригрупповой связи) и мер расстояний между кластерами (расстояние Евклида). Результаты проверки показали устойчивость кластеризации, т.к. все использованные сочетания методов и мер показали одинаковые результаты. Кластерный анализ (табл. 3) допускает три варианта кластеризации. Однако отметим, что вариант I нарушает правило соразмерности кластеров (размер наибольшего кластера не должен превышать величину наименьшего более, чем на 50%) и в силу этого нецелесообразен. Вариант III, по причине излишней детализации, приводит к незначимым различиям средних по каждому группировочному признаку. Оптимальным, в силу сказанного, представляется вариант II, объединяющий федеральные округи в три группы.

Таблица 3

Результаты группировки структур миграционных ситуаций федеральных округов Российской Федерации на основе иерархического кластерного анализа с 2000 по 2015 гг.

Вариант кластеризации	Номер кластера	Регионы
I	1	ЦФО, СЗФО, СФО, ДФО, ПФО, УФО
	2	ЮФО, СКФО
II	1	ЦФО, СЗФО, СФО, ДФО
	2	ПФО, УФО
	3	ЮФО, СКФО
III	1	ЦФО, СЗФО
	2	СФО, ДФО
	3	ПФО, УФО
	4	ЮФО, СКФО

Источник: собственные расчеты автора на основе [1].

Из-за малой наполненности кластеров, сравнения средних производились на основе доверительных интервалов для средней величины. Сравнения доверительных интервалов показали, что по первому признаку (индекс Рябцева с переменой базой сравнения) значительно различаются средние у первого и третьего кластеров. Средние значения индексов Рябцева с постоянной базой сравнения значительно различаются у первого и третьего кластеров, а средние значения по третьему признаку (коэффициент концентрации) у первого и третьего кластеров различаются с 95%-й вероятностью со вторым кластером. Расчет средних значений по попарным сравнениям индексов различия структур федеральных округов не является целесообразным по причине невозможности интерпретации.

Таким образом, в первый кластер входят федеральные округа, структура въездной миграции которых характеризуется наименьшей изменчивостью и динамичностью структурных сдвигов и средним уровнем концентрации (табл. 4). Во второй кластер входят регионы, структура мигрантов по региону исхода которых обладает средней степенью изменчивости и высокой степенью неоднородности. Миграционные структуры федеральных округов, вошедших в третий кластер, можно характеризовать как наиболее изменчивые и наиболее однородные.

Таблица 4

Средние значения признаков по каждому кластеру

Номер кластера	Состав кластера	Индекс Рябцева с переменной базой сравнения	Индекс Рябцева с постоянной базой сравнения	Коэффициент концентрации
1	ЦФО, СЗФО, СФО, ДФО	0,016	0,116	0,185
2	ПФО, УФО	0,020	0,123	0,223
3	ЮФО, СКФО	0,023	0,161	0,177

Источник: собственная разработка автора на основе [2].

Представим графически результаты кластеризации федеральных округов на основе данных о структурах миграционных ситуаций на рисунке. Данные рисунка иллюстрируют, что зачастую схожими являются структуры географически близких федеральных округов. Это объясняется во многом близостью социально-культурных систем и наличием тесных экономических связей между такими регионами. Исключение же составил лишь первый кластер, включивший в себя две пары федеральных округов, разделенных вторым кластером. Таким образом, можно сделать вывод, что миграционные ситуации федеральных округов РФ по признаку регионов исхода мигрантов могут быть сгруппированы в три группы. Каждая из групп обладает уникальными характеристиками, проявляющимися в наименьшей степени различий структур, схожими показателями концентрации и изменчивости.

Стоит отметить, что, несмотря на схожесть структур въездной миграции федеральных округов, вошедших в один кластер, в таких регионах зачастую отмечаются различные показатели интенсивности миграции, определяемые как число въехавших, либо выехавших из региона. Так, например, число въехавших в Центральный федеральный округ в 2015 году составило 223 907 человек, что в 2,65 раза больше, чем число приехавших в Дальневосточный федеральный округ, несмотря на то, что цен- тральный регион России в почти 10 раз меньше по размеру территории [1]. Именно поэтому при прогнозировании и управлении миграционными процессами стоит учитывать не только структурные, но и валовые индикаторы механического движения населения.

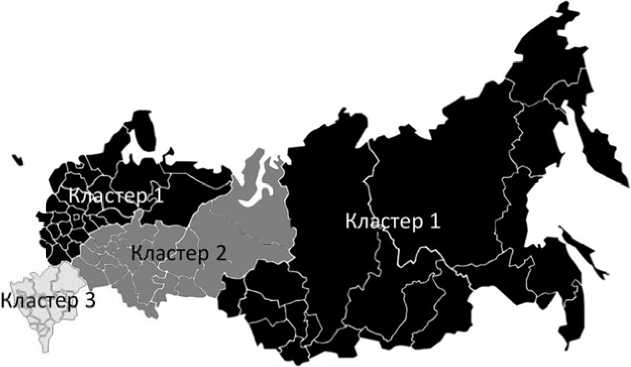
Рис. К арта кластеризации миг р ационных с и туаций фед е ральных ок р угов Россий с кой Федера ц ии ( б ез Республи к и Крым и Севастополя)